Ответ: 14,8 м/с
Задача 2. Тело массой 4 кг перемещается вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью грузом массой 12 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость равен 0,05, угол наклона плоскости равен 30 о . Определите ускорение, с которым движется тело, и силу натяжения нити. Считать, что блок невесом и трение в блоке отсутствует.
ДАНО:  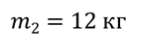    | РЕШЕНИЕ:  Запишем второй закон Ньютона для тела и груза Запишем второй закон Ньютона для тела и груза   В проекциях на ось Ох: В проекциях на ось Ох:  В проекциях на ось Оy: В проекциях на ось Оy:  В проекциях на ось О’y’: В проекциях на ось О’y’: 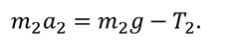 Получаем систему уравнений Получаем систему уравнений 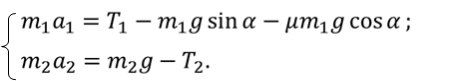 Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то: Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то:  С учётом последних выражений преобразуем систему уравнений С учётом последних выражений преобразуем систему уравнений 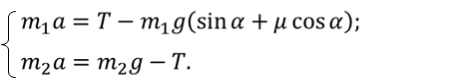 Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим  Преобразуем данное уравнение и выразим искомое ускорение Преобразуем данное уравнение и выразим искомое ускорение    Теперь определим силу натяжения нити Теперь определим силу натяжения нити   |
  |
Ответ: 6,4 м/с 2 ; 43,2 Н.
Задача 3. Два груза массами т1 = 5 кг и т2 = 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю, α = 60 о , β = 30 о , а коэффициент трения — 0,3.
ДАНО: 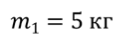   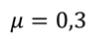  | РЕШЕНИЕ:  Запишем второй закон Ньютона для обоих грузов Запишем второй закон Ньютона для обоих грузов    В проекциях на ось Оx и O’x’: В проекциях на ось Оx и O’x’: 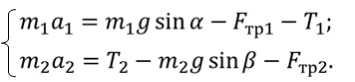 В проекциях на ось Оy и О’у’: В проекциях на ось Оy и О’у’:   С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: 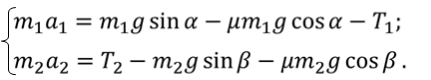 Так как нить и блок невесомы: Так как нить и блок невесомы:  Так как нить нерастяжима и в блоке нет сил трения: Так как нить нерастяжима и в блоке нет сил трения:  С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’: С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’:  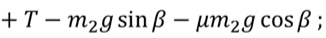  Тогда искомое ускорение равно Тогда искомое ускорение равно     |
 | О |
Ответ:а= 2,6 м/с 2 .
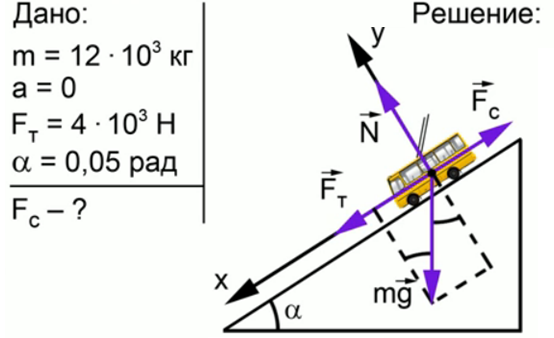
Задача 4. Троллейбус массой 12 т движется равномерно под гору с уклоном 0,05 рад при силе тяги 4 кН. Определить силу сопротивления движению.
Записываем краткое условие задачи и выполняем поясняющий чертеж :
По ох: mg* sin a + Fт – Fc = 0 при а ≤ 0,1 рад а =sin a = tq a
Ответ: 
Тема №3 « Решение задач на движение связанных тел».
Цель: Диагностика знаний учащихся, необходимых для решения задач.
Физический диктант.
Тело движется горизонтально под действием силы F = 2H, масса тела 2кг, ч = 0.2.
Уравнение движения тела x = 3+2t-0,5t 2
Зарисуйте все векторы.
Запишите II закон Ньютона в векторной форме.
Выберите оси координат и запишите закон в проекции на оси.
Найдите вес тела.
Найдите силу давления на поверхность.
Запишите уравнение зависимости Vx(t).
Найдите силу трения Fтр. (2 способа)
Ответы
1)
2) 




3) Fтр-? F = ma N — mg =0 7) 1. Fm=чN N=mg Fm=чmg; Fm=0,2*2кг*10м/с 2 = 4Н;
4) P = N = mg P=20H 2. Fm= ma+ F; Fm= 1*2Н+ 2Н = 4Н
5) Fg = N = 20Н
Закрепление и расширение знаний, умений и навыков в решении задач.
Задача №1.
Два груза, массы которых m1 = 0.1кг; m2 = 0.2кг связаны нитью и лежат на гладкой горизонтальной поверхности. К левому грузу приложена F2 = 0,5H; к правому F1 = 3H. Чему равна сила натяжения нити?
1. Изобразим все векторы сил действующие на тела.
2. Запишем уравнение II закона в векторной форме для каждого тела.
I тело 



II тело 



3. Запишем уравнение в проекциях на координатной оси.
4. Составляем систему:
a = 


5. сделайте вычисления , а так же выясните, изменится ли натяжение нити ,если силы поменять местами.
Задача №2
1. Изобразим все векторы сил действующие на тела.
Обратите внимание: нити две, соответственно силы натяжения разные Т1 и Т2.
2. Запишем уравнение II закона в векторной форме для каждого тела.
I тело: 

II тело: 




III тело: m3 

3. Запишем уравнение в проекциях на координатной оси.
4. Составляем систему:
Дорешайте в числах и найдите силу давления возникающую в оси левого блока (Fg=N) (Силу реакции действующую на ось левого блока)
Задача №3
На гладком столе лежит брусок массой 2кг, на котором лежит тело 1кг. Какую силу нужно приложить к нижнему бруску, чтобы он двигался с а = g/2? Коэффициент трения между брусками 0,5.
1. Изобразим все векторы сил действующие на тела.
Запишем уравнения II закона Ньютона в векторной форме для каждого тела










3. Запишем уравнение в проекциях на координатной оси.
Так как Fтр1 = Fтр2 , то уравнение для 2 го тела в проекции ось Y писать не обязательно!
4.Составляем систему:
F — 2чmg = mа + Ма
F = а(m + М) + 2чmg =1/2 g(m + М) + mg
F = 1/2 g(m + М + 2m) =1/2 g(М + 3m) =1/2 ·10 · 2 = 25 Н..
Задача № 4:
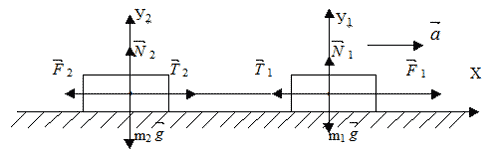
Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н вправо по столу. Массы брусков m1= 1 кг и m2 = 4 кг, μ = 0,1.
С каким ускорением движутся бруски? Чему равна сила натяжения нити?
Ч
Сила натяжения нити на всех участках одинакова и все тела движутся с одним и тем же ускорением, т.е.
Т1 = Т2 = Т, 
Чтобы решить задачу, надо её проанализировать.
Рассмотрим все силы, действующие на каждое тело отдельно. Оба тела взаимодействуют с землёй, столом и нитью. На первое тело действуют: m1g, Т1, Fтр1, N1. На второе тело действуют: m2g, N2, T2,Fтр2 и сила F. Системы отсчета свяжем со столом.

1.Изобразим все силы, действующие на тела. Ускорение тела направлено вправо.
Из условия задачи => Т1 = Т2 = Т; 
2.Запишем II-ой закон Ньютона в общем виде ∑ 


3.Выберем координатные оси: ось ОУ направим по направлению 
а ось ОХ по направлению 
4.Проецируем векторные уравнения II закона Ньютона для I-го и II-го тела на координатные оси:
O 


Поскольку из уравнения 2 =>что Аналогично:
N2 = m2 ∙ g; то Fтр2 =μ · N2=μ ∙ m · g
N1 = m1g; то Fтр1= μ · N1 = μ ∙ m1g, тогда уравнение (1 / )II- го тела примет вид
тогда ур-ние (1)примет видF – T – μ ∙ m2 ∙ g = m2 
Т – μ · m1g = m1 
Получили два уравнения для 2-х тел, где учтены все силы, действующие на тела в отдельности.
Решаем совместно систему уравнений (3)и (3 1 ) методом почленного сложения уравнений, получаем: T – μ m1g + F – T – μ m2g = m1
F – μg (m1+ m2) = 
Откуда 
Силу натяжения нити находим из уравнения (3) или (3 1 )
Т= μ ∙ m1 · g + m1 

или Т = F – m2 

Видео:4.2 Проекция силы на ось координатСкачать

Решение задач на равнопеременное движение в проекциях на координатные оси
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тема сегодняшнего урока: «Решение задач динамики в проекциях на координатные оси». Мы знаем, что основная задача динамики – выяснить причины механического движения. Но существует и обратная задача: зная приложенные к телу силы, рассчитывают его движение. Как раз в этой задаче и применяется метод координат.
Видео:Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Задание 28 ЕГЭ по физике
Механика — квантовая физика. Расчётная задача
При решении расчётной задачи № 28 надо выделять следующие элементы:
- Работа с условием задачи: запись «Дано»,
- представление рисунка, если это необходимо для понимания физической ситуации;
- описание физической модели, т.е. указание на то, какие явления или процессы рассматриваются, какие закономерности можно использовать для решения задачи и чем можно пренебречь, чтобы ситуация отвечала выбранной модели.
- Запись всех необходимых для решения задачи законов и формул, описание используемых физических величин, которые не вошли в «Дано».
- Проведение математических преобразований и расчётов, получение ответа.
Задание № 28 оценивается в 2 балла, так как является типовой расчетной задачей.
1. Сталкиваются и слипаются два разных по массе пластилиновых шарика, причём векторы их скоростей непосредственно перед столкновением направлены навстречу друг другу и одинаковы по модулю: м/с. Во сколько раз масса тяжёлого шарика больше, чем лёгкого, если сразу после столкновения их скорость стала равной (по модулю) 0,5 м/с?
Сделаем чертеж, поясняющий условие задачи.
Применим закон сохранения импульса к системе двух взаимодействующих шаров.
Запись этого закона в векторной форме будет иметь вид:
(1), где – векторы скоростей первого и второго шаров до взаимодействия;
а и – векторы скоростей первого и второго шаров после взаимодействия.
Уравнение (1) в проекциях на выбранную ось ОХ будет иметь вид:
Здесь расставлены знаки проекций скоростей с учетом того, что первый шарик массой М движется по направлению оси ОХ, а второй шарик массой m движется противоположно оси ОХ. Кроме этого, сделано предположение, что после неупругого удара оба шарика будут двигаться по направлению оси ОХ. Это предположение основано на том, что масса левого шарика больше, чем правого, а модули скоростей до взаимодействия одинаковы.
Выразим из уравнения (2) отношение масс .
Подставим численные значения и проведем расчет.
Секрет решения. При решении задач по теме «Закон сохранения импульса» необходимо соблюдать определенный алгоритм (последовательность действий):
- Записать закон сохранения импульса для системы взаимодействующих тел в векторном виде.
- Выбрать ось ОХ (или ОY), на которую надо спроецировать проекции тел до и после взаимодействия.
- Учесть вид взаимодействия (абсолютно упругий или абсолютно неупругий удар).
- Сделать предположение о движении тел после взаимодействия.
- Составить уравнение и решить его относительно неизвестной величины.
Этот алгоритм (последовательность действий) является необходимым инструментом при решении подобных задач. Вероятность того, что на ЕГЭ встретится точно такая же задача, очень мала. Особенно это справедливо для второй части. Только вооружившись данным методом решения задач, можно надеяться на успех.
2. Груз массой 120 кг удерживают с помощью рычага, приложив к его концу вертикально направленную силу 300 Н (см. рисунок). Рычаг состоит из шарнира без трения и длинного однородного стержня массой 30 кг. Расстояние от оси шарнира до точки подвеса груза равно 1 м. Определите длину стержня.
На рисунке отметим силы, приложенные к рычагу.
– сила тяжести стержня. С учетом того, что стержень однородный, центр тяжести расположен посередине.
– сила реакции, действующая со стороны опоры на стержень.
– вес груза массой М, который действует на стержень.
Для рычага, находящегося в равновесии, алгебраическая сумма моментов сил равна нулю.
Рассмотрим моменты сил относительно точки опоры.
Момент силы реакции опоры равен нулю, так как плечо этой силы относительно точки опоры равно нулю.
Будем считать моменты сил, вращающих рычаг против часовой стрелки, положительными, а моменты сил, вращающих рычаг по часовой стрелке, отрицательными.
Решим это уравнение относительно L.
Подставим численные значения и проведем расчет.
Секрет решения. Решение подобных задач сводится к составлению уравнений, выражающих условия равновесия тел.
Первое условие: векторная сумма сил, приложенных к телу, равна нулю.
Второе условие: алгебраическая сумма моментов сил, приложенных к телу, равна нулю.
Сложности в этой теме связаны с определением плеч сил. Надо помнить, что плечо – это кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила.
Если в задаче дается тело, находящееся на двух опорах, то, возможно, потребуется составление условия равновесия через моменты сил для двух точек С и D опоры (рис. 1)
Главное, надо помнить, что для решения системы уравнений необходимо, чтобы число неизвестных было равно числу независимых уравнений.
3. Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускорено. Опустившись на 2 м, левый груз приобрёл скорость 4 м/с. Определите силу натяжения нити, если масса правого груза m = 1 кг. Трением пренебречь.
Укажем все силы, которые действуют на грузы массой М и m.
– сила тяжести, действующая на груз массой М.
– сила тяжести, действующая на груз массой m.
– сила натяжения нити, действующая на груз массой М.
– сила натяжения нити, действующая на груз массой m.
Составим уравнение движения для каждого груза на основании второго закона Ньютона:
Запишем эти уравнения в проекциях на ось OY.
Так как нить невесома и нерастяжима, а блок идеальный, то
Тогда уравнения (1) и (2) примут вид:
Для нахождения силы натяжения нити достаточно воспользоваться уравнением под номером 4. Из него можно выразить силу натяжения нити Т.
Из кинематической формулы с учетом равенства нулю начальной скорости найдем ускорение системы тел.
Подставив ускорение в формулу (5), получим:
Проведем расчет силы натяжения нити:
Секрет решения. При решении задач по темам «Движение связанных тел», «Движение тел по наклонной плоскости» необходимо использовать следующий алгоритм (последовательность действий):
- Указать на чертеже (рисунке) все силы, приложенные к каждому телу.
- Составить уравнение движения для каждого тела в векторном виде на основе второго закона Ньютона.
- Выбрать оси координат ОХ и ОY и записать уравнения движения в проекциях на выбранные оси.
- Составить систему уравнений и решить ее относительно неизвестной величины.
- Подставить численные значения и провести расчет.
Иногда, при использовании этого алгоритма, возникает вопрос о направлении осей ОХ и ОY, куда направить «стрелочки», вверх-вниз, вправо-влево? Это не имеет никакого значения, больше того, для одного тела направление оси можно выбрать вверх, а для другого вниз. Это равносильно тому, что математическое уравнение можно умножить (разделить) на (-1), от этого равенство не изменится.
📽️ Видео
Урок 9. Проекции вектора на координатные осиСкачать

Проекция перемещения на ось XСкачать

Векторные величины Проекция вектора на осьСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Построение проекции вектора на осьСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Как проецировать скорости на оси в кинематике через Синус и Косинус?Скачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение движенияСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Проекция силы на осьСкачать
Задача: 2 закон Ньютона и проекции на осиСкачать

§4 Проекция вектора на осьСкачать
Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

⚙️ Механика: вся кинематика с нуля | Физика ЕГЭ 2024 | УмскулСкачать