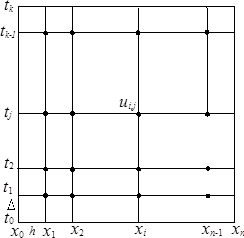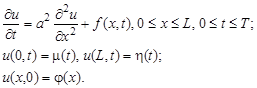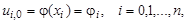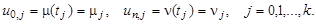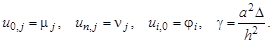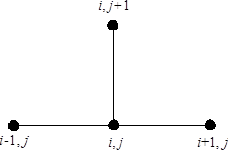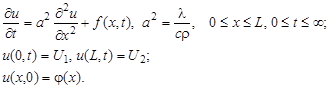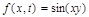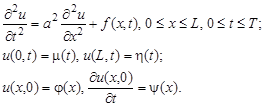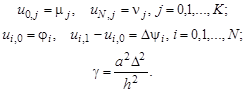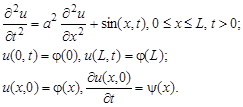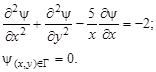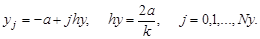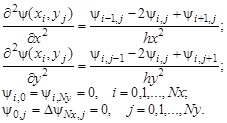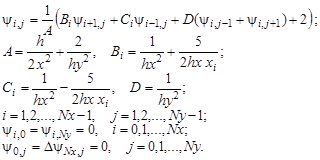Уравнение в частных производных метод сеток

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных

Одним из наиболее распространенных численных методов решения уравнений в частных производных является метод сеток. В методе сеток область Ω, в которой необходимо найти решение уравнения, разобьем прямыми, параллельными осям и , на прямоугольные области (рис.1.1), где

,

.

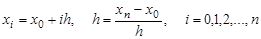
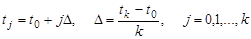
Точки, которые лежат на границе области Ω, называются внешними, остальные точки – внутренними. Совокупность всех точек называется сеткой, величины h и Δ – шагами сетки по хи t соответственно.

Рис.1.1. Сетка 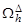для области Ω

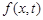
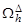
Идея метода сеток состоит в том, что вместо любой непрерывной функции будем рассматривать дискретную функцию , которая определена в узлах сетки , вместо производных функции будем рассматривать их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получим систему алгебраических уравнений. Чем меньше величины h иΔ, тем точнее получаемые алгебраические уравнения моделируют исходное дифференциальное уравнение в частных производных. В этом и последующих подразделах этой главы будет рассмотрен метод сеток для каждого из трех типов уравнений и его реализация в MATLAB. Знакомство с численными методами решения дифференциальных уравнений в частных производных начнем с разностных схем решения параболических уравнений.

Разностные схемы решения параболических уравнений будем рассматривать на примере следующего одномерного уравнения:

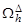
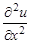
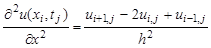
Построим сетку (см. рис.1.1). Для получения сеточного уравнения заменим производную приближенной разностной формулой:

.

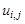
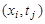
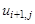
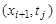
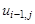
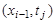
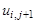
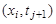
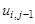
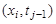
В этой и последующих формулах – значение функции u в точке , – в точке , – в точке , – в точке , – в точке .

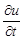
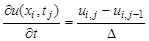
Для замены можно воспользоваться одной из приближенных разностных формул

;

.

Кроме того, заменим начальные и граничные условия их разностной аппроксимацией:

Заменив частные производные в задаче соответствующими разностными соотношениями, получим следующую вычислительную схему для расчета значений функции и в узлах сетки :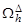

;

Это явная двухслойная разностная схема (рис.1.2).

Рис.1.2. Шаблон явной двухслойной разностной схемы

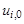
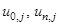
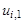
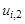
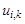
Учитывая, что на нулевом слое (при i = 0)все значения (как, впрочем, и ) известны, можно сначала явно рассчитать значения , затем и так до .Для устойчивости разностной схемы значения шагов по t и х должны удовлетворять следующему условию:

.

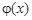
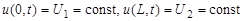
Пример. Решить параболическое уравнение, описывающее распределение температуры в стержне длиной L,начальная температура стержня задается произвольной функцией . Температуры концов стержня равны .

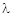
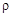
Здесь а 2 – коэффициент температуропроводности; – коэффициент теплопроводности материала стержня; с – удельная теплоемкость; – плотность массы.

Подпрограмма решения задачи с помощью явной разностной схемы в MATLAB:

//Правая часть дифференциального уравнения

//Условие на левой границе

//Условие на правой границе

//Функция решения параболического уравнения методом сеток с помощью явной разностной схемы. N — количество участков разбиения интервала по х (0,1_); К – количество участков разбиения интервала по t (0,Т); а — коэффициент температуропроводности,

// Функция возвращает матрицу решений u вектора х, t

// Вычисляем шаг по х

// Вычисляем шаг по t

// Формируем массив х и первый столбец матрицы решений u

// из начального условия

//Формируем массив t, первую и последнюю строку матрицы решений u из граничных условий

gam = a ^ 2*delta/h ^ 2;

// Формируем матрицу решений u

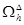
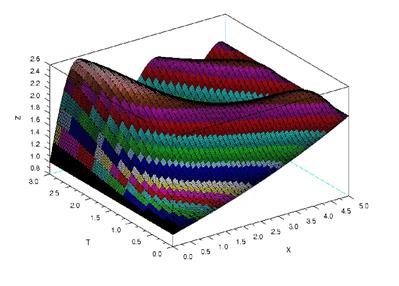
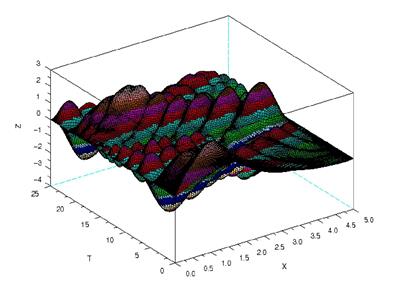
Входными данными подпрограммы parabol решения задачи являются: N – количество интервалов, на которые разбивается отрезок (О, L); К – количество интервалов, на которые разбивается отрезок (О, Т); L – длина стержня, Т – интервал времени, а – параметр дифференциального уравнения. Функция возвращает три параметра: решение – сеточная функция u, определенная на сетке , массивы x и t.

График решения данной задачи изображен на рис.1.3.

Рис.1.3. График решения параболического уравнения при

1.4.2. Использование метода сеток для решения гиперболических уравнений

Решение гиперболических уравнений также можно осуществить с помощью разностных схем. Разностные схемы решения одномерного гиперболического уравнения рассмотрим на примере следующего уравнения:

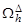
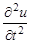
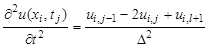
Построим сетку , в которой будем искать решение уравнения. Производную заменим соотношением:

,

остальные производные такие же, как и в предыдущем подразделе.

Получим следующую явную разностную схему решения уравнения:

Она устойчива при 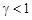и по аналогии с разностной схемой (см. подразд. 1.4.1) может быть легко запрограммирована в MATLAB.

В качестве примера рассмотрим следующую задачу.

Пример. Решить начально-граничную задачу:

Ниже представлена функция giperbol решения данного уравнения, а на рис.1.4 – график полученного решения. Параметры функциианалогичны рассмотренным ранее, т.е. в подпрограмме решения параболического уравнения.

//Функция решения гиперболического уравнения с помощью явной разностной схемы. Входные данные: N — количество участков разбиения интервала (0,L); K — количество участков разбиения интервала (0,T); a — коэффициент теплопроводности; u — матрица решений в узлах сетки; массив x; массив t,

// Вычисляем шаг по х и по t

//Формируем массив x, первый и второй столбцы матрицы решений u из начального условия

//Формируем массив t, первую и последнюю строки матрицы решений u из граничных условий

//Формируем первую и последнюю строки матрицы решений u из граничных условий

//Формируем матрицу решений u

Рис.1.4. График решения гиперболического уравнения

1.4.3. Использование метода сеток для решения эллиптических уравнений

Разностные схемы решения одномерного эллиптического уравнения рассмотрим на следующем примере.

Пример. Рассмотрим разностную схему для эллиптического уравнения в прямоугольной области 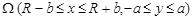с граничными условиями Дирихле на границе Г:

Проведем в области Ω прямые, параллельные осям и , где ;

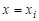
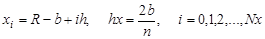
Для построения разностного уравнения заменим частные производные и граничные условия следующими соотношениями:

Преобразуем данную эллиптическую краевую задачу к следующей системе разностных уравнений:

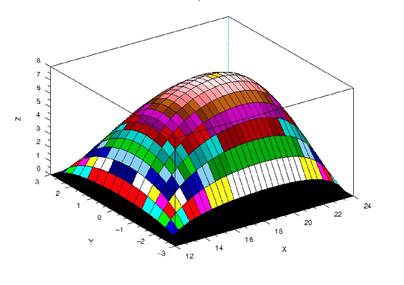
Эту систему можно решать итерационными методами (например, методом Зейделя). В случае медленной сходимости итерационных процессов при решении сеточных уравнений, получаемых при аппроксимации гиперболических и эллиптических задач, можно попробовать заменить метод Зейделя градиентными методами (или методами релаксации). Ниже представлено решение эллиптического уравнения сеточным методом, а на рис.1.5 график полученного решения.

Рис.1.5. График решения эллиптического уравнения

// Функция ellip решения задачи

// Входные данные:R, a, b — значения, определяющие область решения задачи; Nx — количество участков разбиения интервала(R-b,R+b); Ny — количество участков разбиения интервала(-a,a); eps — точность решения уравнения методом Зейделя.

// psi — матрица решений в узлах сетки, массив x, массив y, k — количество итераций при решении разностного уравнения

// Вычисляем шаг по y и по x

// Формируем массив x, первый и последний столбцы матрицы решений psi из граничного условия

// Формируем массив y, первую и последнюю строки матрицы решений psi из граничного условия

// Вычисляем коэффициенты разностного уравнения

//Решение разностного уравнения методом Зейделя

Видео:Простейшие уравнения в частных производныхСкачать

Численные методы решения краевых задач

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Постановка задачи и основные положения

Рассмотрим двухточечные краевые задачи, часто встречающиеся в приложениях, например, при решении задач вариационного исчисления, оптимального управления, механики жидкости и газа и др. Пусть дано обыкновенное дифференциальное уравнение

и краевые условия

где [math]F bigl(x,y,y’,ldots,y^bigr);

j=overline[/math] — функции указанных аргументов, заданные в некоторой области их изменения; [math]L[/math] и [math](n-L)[/math] — число условий на левом и правом концах отрезка [math][a,b][/math] соответственно. Общее количество условий равно порядку дифференциального уравнения. Требуется найти функцию [math]y=y(x)[/math] , которая на отрезке [math][a,b][/math] удовлетворяет уравнению (7.1), а на концах отрезка — краевым условиям (7.2).

Если уравнения (7.1),(7.2) линейны относительно искомой функции и ее производных, то краевая задача называется линейной.

Для простоты ограничимся частным случаем линейной краевой задачи для дифференциального уравнения второго порядка [math](n=2)[/math] , которая наиболее часто ставится в вычислительной практике и записывается в виде

(Omega equiv [a,b]),[/math]

где [math]p(x),, q(x),, f(x)in C_2[a,b][/math] — заданные функции, а [math]alpha_0,,alpha_1,, beta_0,, beta_1,,A,,B[/math] — заданные числа, 0,

j=0;1[/math] . Требуется найти функцию [math]y(x)[/math] , удовлетворяющую уравнению (7.3) и краевым условиям (7.4). Краевые условия при [math]alpha_ne0,

j=0;1[/math] , задают линейную связь между значениями искомого решения и его производной на концах отрезка [math][a,b][/math] .

В простейшем случае, когда [math]beta_0=0,

beta_1=0[/math] , краевые условия задают на концах отрезка [math][a,b][/math] только значения функции [math]y(a),,y(b)[/math] . Такие функциональные условия называют краевыми условиями первого рода. В этом случае краевая задача называется первой краевой задачей.

В случае, когда [math]alpha_0=0,

alpha_1=0[/math] , т.е. на концах отрезка заданы только значения производных, краевые условия являются дифференциальными. Такие краевые условия называют условиями второго рода или «мягкими». Последнее название обусловлено тем, что они определяют на концах отрезка [math][a,b][/math] всего лишь наклоны интегральных кривых, а не значения функции [math]y(x)[/math] . В этом случае задача (7.3),(7.4) называется второй краевой задачей.

В общем случае, когда [math]alpha_0[/math] и (или) [math]alpha_1;

beta_0[/math] и (или) [math]beta_1[/math] не равны нулю, краевые условия носят функционально-дифференциальный характер и называются условиями третьего рода. Тогда задача (7.3),(7.4) называется третьей краевой задачей.

Например, условия [math]y(a)=A,

y(b)=B[/math] являются условиями первого рода. Геометрически это означает, что при решении первой краевой задачи требуется найти интегральную кривую уравнения (7.3), проходящую через данные точки [math](a,A),, (b,B)[/math] (рис. 7.1,а). Условия [math]y'(a)=A,, y'(b)=B[/math] являются условиями второго рода. Геометрически вторая краевая задача сводится к отысканию интегральной кривой уравнения, пересекающей прямые [math]x=a,

x=b[/math] под заданными углами [math]alpha,,beta[/math] , где [math]operatornamealpha=A,

operatornamebeta=B[/math] (рис. 7.1,6). Условия [math]y'(a)=A,

y(b)=B[/math] являются частным случаем краевых условий третьего рода, так как [math]alpha_0=0,

beta_1=0[/math] . Геометрически данная краевая задача сводится к отысканию интегральной кривой уравнения, проходящей через точку [math](b,B)[/math] и пересекающей прямую [math]x=a[/math] под данным углом [math]alpha[/math] , где [math]operatornamealpha= A[/math] (рис. 7.1,в).

В общем случае краевая задача может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь несколько или бесконечно много решений.

Утверждение 7.1 (о существовании и единственности решения краевой задачи (7.3),(7.4)). Для того чтобы существовало единственное решение краевой задачи (7.3),(7.4), необходимо и достаточно, чтобы однородная краевая задача

имела только тривиальное решение [math]y(x)equiv0[/math] .

Пример 7.1. Найти аналитическое решение следующих краевых задач:

0 leqslant x leqslant frac,

y! left(fracright)-y’! left(fracright)=2[/math] (третья краевая задача);

0 leqslant x leqslant 1,

y(1)=0[/math] (первая краевая задача).

Воспользуемся известной методикой отыскания общих решений дифференциальных уравнений. Подставив в них заданные краевые условия, получим аналитические решения данных краевых задач.

1. Найдем общее решение однородного уравнения [math]y»+y=0[/math] , одинакового для обеих рассматриваемых задач. Так как характеристическое уравнение [math]lambda^2+1=0[/math] имеет комплексные сопряженные корни [math]lambda_=pm i= alphapm beta i[/math] [math](alpha=0,

beta=1)[/math] , то общее решение будет

2. Частные решения неоднородных уравнений находятся методом подбора. Подставляя [math]y_<text>(x)=C[/math] в уравнение [math]y»+y=1[/math] , а [math]y_<text>(x)=Dx[/math] в уравнение [math]y»+y=-x[/math] , получаем [math]C=1,

D=-1[/math] . Поэтому [math]y_<text>(x)=1[/math] в случае «а», [math]y_<text>(x)=-x[/math] в случае «б».

3. Найдем общее решение неоднородного уравнения как сумму общего решения однородного уравнения и частного решения неоднородного уравнения:

а) [math]y(x)=C_1cos x+C_2sin x+1[/math] ; б) [math]y(x)=C_1cos x+C_2sin x-x[/math] .

4. Определим значения произвольных постоянных из краевых условий третьего рода (случай «а») и первого рода (случай «б»):

а) найдем [math]y'(x)=-C_1sin x+C_2cos x[/math] . Тогда

Отсюда [math]C_1=1[/math] и [math]y(x)=1+cos x[/math] — решение краевой задачи «а»;

б) общее решение [math]y(x)=C_1cos x+C_2sin x-x[/math] и, следовательно, [math]y(0)=C_1=0,

y(1)=C_1cos1+ C_2sin1-1=0[/math] , отсюда [math]C_2= frac[/math] и [math]y(x)=frac-x[/math] — решение краевой задачи «б». Таким образом, решение краевой задачи представляет собой такое частное решение, которое удовлетворяет краевым условиям.

Рассмотренный метод нахождения аналитического решения краевых задач применим для ограниченного класса задач. Поэтому в вычислительной практике используются численные и приближенно-аналитические методы, позволяющие найти приближенное решение краевых задач, точные аналитические решения которых не могут быть найдены.

Видео:6-2. Метод сетокСкачать

Метод сеток

Рассмотрим линейную краевую задачу с краевыми условиями первого рода (первую краевую задачу):

где [math]p(x),q(x),f(x)in C_2[a,b][/math] — заданные функции; [math]A,,B[/math] — заданные числа.

Очевидно, любой отрезок [math][a,b][/math] , на котором ищется решение краевой задачи, можно привести к отрезку [math][0;1][/math] с помощью линейного преобразования [math]widetilde= frac[/math] . Действительно, тогда новая переменная [math]widetildein [0;1][/math] . В результате без ограничения общности краевая задача (7.5) может быть решена сначала на отрезке [math][0;1][/math] , а затем это решение с помощью преобразования [math]x=a+(b-a)cdot widetilde[/math] может быть записано на отрезке [math][a,b][/math] . То же относится и к исследованию свойств полученного решения.

Утверждение 7.2 (о единственности решения краевой задачи (7.5)). Если функции [math]p(x),q(x),f(x)[/math] принадлежат классу [math]C_2[a,b],

q(x) geqslant 0[/math] на [math][0;1][/math] , то краевая задача (7.5) имеет единственное решение [math]y(x)in C_4[0;1][/math] .

Для решения задачи (7.5) применим метод сеток, получаемый путем аппроксимации первой и второй производных. Введем равномерную сетку (где [math]n[/math] — число отрезков разбиения)

Функции [math]p(x),q(x),f(x)[/math] заменяются их проекциями на сетку [math]Omega_n[/math] , то есть [math]p(x)to p(x_)=p_i,[/math] [math]q(x)to q(x_)=q_i,[/math] [math]f(x)to f(x_)= f_i,[/math] . Вместо точного решения [math]y(x)[/math] отыскивается некоторое приближение [math]widehat_= widehat(x_)approx y(x_),

i=overline[/math] . Первая и вторая производные аппроксимируются на трехточечном шаблоне [math](x_,x_,x_)[/math] по формулам второго порядка (5.10),(5.14):

Краевые условия для этой задачи аппроксимируются точно, т.е. [math]y(a)[/math] и [math]y(b)[/math] заменяются на [math]widehat_[/math] и [math]widehat_[/math] . После замены от дифференциальной задачи (7.5) переходим к разностной схеме:

представляющей собой систему алгебраических уравнений трехдиагонального вида:

delta_=f_[/math] . Здесь система (7.6) записана для внутренних узлов сетки [math]Omega_n[/math] . Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.

1. Изложенный метод сеток допускает обобщение. Например, его можно применять для решения нелинейной краевой задачи:

где [math]F(x,y)[/math] — нелинейная по [math]y[/math] функция (в общем случае, который здесь не рассматривается, функция [math]F[/math] зависит также и от [math]y'[/math] ).

Рассуждая аналогично рассмотренному выше способу, перейдем к разностной задаче:

В силу нелинейности правой части полученная алгебраическая система является нелинейной и для ее решения нельзя использовать метод прогонки в том виде, в каком он изложен для линейной задачи. Поэтому для ее решения используем метод простых итераций, с помощью которого при фиксированном [math]k[/math] (номер итерации) система алгебраических уравнений (7.8) превращается в линейную, так как величины, входящие в правую часть системы, известны из предыдущей итерации. Действительно, для k-й итерации получается система (которая решается на каждой итерации методом прогонки)

Можно показать, что итерации сходятся при выполнении условия [math]q=frac(x_n-x_0)^2M_1 [math]M_1=max_left|fracright|[/math] с линейной скоростью.

2. Краевые условия второго и третьего рода в задаче, аналогичной (7.5), могут быть аппроксимированы несколькими способами.

Первый способ. Использование аппроксимационных формул (5.4) первого порядка

В силу первого порядка этих аппроксимаций метод сеток в этом случае также будет иметь первый порядок аппроксимации.

Второй способ. Применение формулы Тейлора и ее преобразование с использованием дифференциального уравнения. Таким способом может быть достигнут второй порядок аппроксимации.

Третий способ. Применение левосторонней (5.8) и правосторонней (5.9) формул, аппроксимирующих производные со вторым порядком:

3. Порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Алгоритм применения метода сеток

1. Задать сетку [math]Omega_n[/math] на отрезке [math][a,b][/math] или сформировать ее из условий достижения требуемой точности.

2. Используя аппроксимационные формулы (5.10),(5.14) и один из трех способов аппроксимации краевых условий (в случае, если они второго или третьего рода), перейти от исходной дифференциальной задачи к системе алгебраических уравнений (разностной схеме), неизвестными в которой являются величины, «близкие» к решению краевой задачи в узлах сетки.

3. Найти решение разностной задачи путем решения трехдиагональной системы уравнений и таким образом определить приближенное решение краевой задачи.

Пример 7.2. Найти приближенное решение краевой задачи [math]y»+y=1,

0 leqslant x leqslant frac,[/math] [math]y'(0)=0,[/math] [math]y! left(fracright)-y’! left(fracright)=2[/math] при [math]n=3[/math] , используя первый способ аппроксимации краевых условий. Записать разностные схемы для второго и третьего способов при произвольном [math]n[/math] .

В поставленной задаче

Для решения задачи воспользуемся методикой.

1. Так как [math]n=3[/math] , то сетка имеет вид [math]Omega_3=[/math] , где [math]x_=ih,

y! left(fracright)=y_1,[/math] [math]y! left(fracright)=y_2,[/math] [math]y! left(fracright)=y_3[/math] . Будем искать приближенные значения [math]widehat_0,widehat_1, widehat_2, widehat_3[/math] . Проекции функций [math]p(x), q(x), f(x)[/math] на сетку имеют вид [math]p_=0,

2. Составим разностную схему. Согласно (7.6), для внутренних узлов сетки получаем

i=1;2[/math] или [math]widehat_-(2-h^2)widehat_+ widehat_=h^2,

Применим первый способ аппроксимации краевых условий. По формуле (5.4) с учетом условия [math]y'(0)=0[/math] на левом конце имеем

На правом конце [math]y! left(fracright)=y_3,

y’! left(fracright)=y’_3[/math] , и по второй из формул (7.9) [math]widehat,’_= frac<widehat_-widehat_>[/math] . Тогда краевое условие [math]y! left(fracright)-y’! left(fracright)=2[/math] аппроксимируется выражением

В результате получаем разностную схему первого порядка аппроксимации (трехдиагональную систему линейных алгебраических уравнений)

Сравнивая первое уравнение этой системы с рекуррентным соотношением [math]widehat_= P_cdot widehat_+ Q_[/math] метода прогонки, характеризующим обратный ход, получаем [math]P_0=1,

После этого вычисляются все последующие прогоночные коэффициенты по формулам:

Здесь [math]alpha_,beta_,gamma_[/math] соответствуют коэффициентам левой части полученной алгебраической системы, а [math]delta_[/math] — правой части.

Далее выполняется обратный ход: [math]widehat_=Q_3,

widehat_= P_2widehat_+ Q_2,

widehat_= P_1widehat_+ Q_1[/math] .

Результаты решения краевой задачи приведены в табл. 7.1, в которой последний столбец соответствует точному решению [math]y(x)=1+cos x[/math] , найденному в примере 7.1.

7.1>>\hline i& alpha_& beta_& gamma_& delta_& P_& Q_& widehat_& y(x) \hline 0& 0&-1,!0000&-1& 0,!00000& 1,!00000& 0& 1,!8648& 2,!0000\hline 1& 1& 1,!72584& 1& 0,!27415& 1,!37771&-0,!37770& 1,!8648& 1,!8666\hline 2& 1& 1,!72584& 1& 0,!27415& 2,!87240&-1,!87242& 1,!6277& 1,!5000\hline 3& 1& 0,!47640&-& 1,!04200&-& 1,!21853& 1,!21853& 1,!0000\hline end[/math]

В силу того, что краевые условия аппроксимированы с первым порядком относительно [math]h[/math] , в данном случае получена разностная схема первого порядка, так как порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.

Воспользуемся вторым способом аппроксимации краевых условий для построения разностной схемы второго порядка аппроксимации. Разложим [math]y(x)[/math] в точке [math]x=x_1[/math] относительно точки [math]x_0[/math] по формуле Тейлора:

Выразим из этого соотношения [math]y'(x_0)[/math] и подставим в него вместо [math]y»(x_0)[/math] выражение [math]y»(x_0)=1-y(x_0)=1-y_0[/math] , определяемое исходным дифференциальным уравнением:

Как показывает это соотношение, дифференциальное условие на левой границе аппроксимируется на двухточечном шаблоне [math](x_0,x_1)[/math] со вторым порядком аппроксимации двухточечным алгебраическим уравнением:

Аналогично получается двухточечное алгебраическое уравнение при / [math]i=n-1[/math] и [math]i=n[/math] . Разложение [math]y(x)[/math] в точке [math]x=x_[/math] относительно точки [math]x_n[/math] по формуле Тейлора имеет вид

Выражая отсюда [math]y'(x_n)[/math] с учетом связи [math]y»(x_n)=1-y(x_n)=1-y_n[/math] , следующей из исходного дифференциального уравнения, получаем

Подставим это выражение в граничное условие:

Таким образом, система линейных алгебраических уравнений в окончательном виде записывается следующим образом:

Эта трехдиагональная система, отличающаяся от полученной первым способом только первым и последним уравнениями, решается численно методом прогонки.

Применим третий способ аппроксимации краевых условий для построения разностной схемы второго порядка. Так, для крайней левой точки используется левосторонняя формула (5.8):

Тогда получается трехточечное алгебраическое уравнение:

Аппроксимация производной [math]y’! left(fracright)[/math] в крайней правой точке по правосторонней формуле [math]widehat,’_= frac bigl(widehat_-4widehat_+ 3widehat_bigr)[/math] приводит к трехточечному алгебраическому уравнению:

Тогда в этом случае получается следующая система линейных алгебраических уравнений:

Здесь [math]widehat_[/math] в первом уравнении и [math]widehat_[/math] в последнем нарушают ее трехдиагональный характер. В этом случае система приводится к трехдиагональному виду путем исключения [math]widehat_[/math] и [math]widehat_[/math] из первых двух и последних двух уравнений системы и после этого решается методом прогонки.

Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

Методы минимизации невязки

Описываемые здесь методы относятся к приближенно-аналитическим и могут применяться при решении достаточно широкого класса задач. На основе одного из приближенно-аналитических методов (метода Галеркина) строится метод конечных элементов, излагаемый в разд. 7.5.

Рассмотрим линейную краевую задачу (7.3),(7.4). Ее решение будем искать в виде

где [math]varphi_0(x), varphi_1(x), ldots, varphi_m(x)[/math] — элементы заданной системы функций; [math]a_1,ldots,a_m[/math] — неопределенные коэффициенты. Заданная система функций называется базисной, и ее элементы должны удовлетворять условиям:

а) [math]varphi_(x)in C_2[a,b],

б) при любом конечном [math]m[/math] функции [math]varphi_1(x), ldots, varphi_m(x)[/math] линейно независимы на отрезке [math][a,b][/math] ;

в) [math]varphi_0(x)[/math] удовлетворяет краевым условиям (7.4)

г) [math]varphi_1(x), ldots, varphi_m(x)[/math] удовлетворяют условиям

называется невязкой . Она равна разности левой и правой частей уравнения (7.3), образующейся при подстановке [math]widehat_(x)[/math] вместо [math]y(x)[/math] в дифференциальное уравнение, и характеризует степень отклонения функции [math]widehat_(x)[/math] от точного решения краевой задачи. Если при некоторых значениях коэффициентов [math]a_1,ldots,a_m[/math] невязка тождественно равна нулю на отрезке [math][a,b][/math] , а именно

то функция [math]widehat_(x)[/math] совпадает с точным решением краевой задачи (7.3),(7.4), так как удовлетворяются и уравнение, и краевые условия.

Однако при решении краевых задач, как правило, не удается получить невязку тождественно равной нулю. Поэтому ставится задача: вычислить коэффициенты [math]a_1,ldots,a_m[/math] таким образом, чтобы невязка в каком-либо смысле стала меньшей. Полученные в результате коэффициенты определяют приближенное решение (7.11).

Выражение для невязки [math]varepsilon(x; a_1,ldots, a_m)[/math] с учетом (7.11) удобно записывать в следующей эквивалентной форме:

где [math]Lwidehat_equiv widehat,»_(x)+ p(x)widehat,’_(x)-q(x) widehat_(x),

L[/math] — линейный оператор задачи (7.3),(7.4) (выполняются равенства [math]L(y+z)= Ly+Lz,[/math] [math]L(Cy)=Ccdot Ly[/math] для любых [math]y,,z[/math] и постоянной [math]C[/math] ).

Рассмотрим различные методы, минимизирующие невязку .

А. Метод коллокации. На интервале [math](a,b)[/math] задаются т точек [math]x_1,ldots, x_n[/math] (точек коллокации) и требуется, чтобы в каждой из них невязка (7.14) обращалась в нуль:

С учетом (7.16) эта система принимает вид

Если полученная система [math]m[/math] линейных уравнений совместна, то из нее определяются коэффициенты [math]a_1,ldots, a_m[/math] , которые затем подставляются в (7.11).

Б. Метод наименьших квадратов (непрерывный вариант). Неизвестные коэффициенты [math]a_1,ldots, a_m[/math] должны обеспечивать минимум интеграла от квадрата невязки:

Для решения задачи применяются необходимые условия безусловного экстремум:

Подставляя (7.16) в (7.19), получаем систему [math]m[/math] линейных алгебраических уравнений для нахождения коэффициентов [math]a_1,ldots, a_mcolon[/math]

В. Метод наименьших квадратов (дискретный вариант). Неизвестные коэффициенты [math]a_1,ldots,a_m[/math] должны обеспечивать минимум суммы квадратов значений невязки в заданном наборе точек [math]x_1,ldots,x_n;

n geqslant m[/math] , то есть [math]x_in (a,b),

Для решения задачи применяются необходимые условия безусловного экстремума

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов [math]a_1,ldots,a_m[/math] , которая по форме записи совпадает с (7.20), но скалярное произведение определяется по формуле [math]textstyle<(f,g)= sumlimits_^ f(x_)g(x_)>[/math] .

Замечание. При [math]n=m[/math] результаты, полученные точечным методом наименьших квадратов и методом коллокации, совпадают. В этом случае точки [math]x_1,ldots, x_n[/math] являются точками коллокации.

Г. Метод моментов (взвешенных невязок). Неизвестные коэффициенты ах. ат находятся из условия равенства нулю /и моментов невязки:

j=overline[/math] — функции, удовлетворяющие условиям:

б) функции [math]psi_(x)[/math] являются элементами системы степеней [math]x[/math] или системы тригонометрических функций.

j=overline[/math] называются весовыми, а условие (7.22) является условием ортогональности невязки к весовым функциям.

Д. Метод Галсркина. Он является частным случаем метода моментов, когда в качестве весовых функций используются базисные. Коэффициенты [math]a_1,ldots,a_m[/math] находятся из условия ортогональности функций базисной системы [math]varphi_1(x),ldots, varphi_(x)[/math] к невязке:

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов:

Известно, что при достаточно большом [math]m[/math] условие (7.23) обеспечивает малость невязки в среднем.

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Алгоритм применения методов минимизации невязки

1. В выражении (7.11) выбрать систему базисных функций, задать число [math]m[/math] в зависимости от требуемой точности.

2. Найти коэффициенты [math]a_1,ldots,a_m[/math] путем решения одной из систем алгебраических уравнений (7.18),(7.20),(7.24) в зависимости от выбранного метода.

3. Выписать приближенное решение краевой задачи по формуле (7.11).

Пример 7.3. Найти приближенное решение краевой задачи [math]y»+y=-x,

0 leqslant x leqslant 1,[/math] [math]y(0)=0,

y(1)=0[/math] методом коллокации, интегральным методом наименьших квадратов, методом Галеркина

В поставленной задаче

Точное решение найдено в примере 7.1.

Воспользуемся сначала методом коллокации.

1. Зададим [math]m=2[/math] и будем искать решение в виде

где [math]varphi_0(x)equiv0[/math] (эта функция удовлетворяет каждому из краевых условий, т.е. [math]varphi_0(0)=0,

varphi_0(1)=0[/math] ), функции [math]varphi_1(x)= x(1-x),

varphi_2(x)= x^2(1-x)[/math] . Функции [math]varphi_1(x),, varphi_2(x)[/math] линейно независимые, дважды непрерывно дифференцируемые и удовлетворяют условию (7.13). Действительно,

Таким образом, решение краевой задачи ищется в форме

2. Так как [math]m=2[/math] и [math]varphi_0(x)equiv 0[/math] , то система (7.18) имеет вид

Выберем узлы коллокации: [math]x_1=1!!not<phantom>,4,

Таким образом, имеем линейную систему относительно [math]a_1[/math] и [math]a_2colon[/math]

3. Приближенное решение задачи: [math]widehat_2(x)= frac(42+40x)[/math] .

Решим теперь задачу методом наименьших квадратов (см. непрерывный вариант).

1. Решение краевой задачи ищется в форме [math]widehat_2(x)= a_1cdot x(1-x)+ a_2cdot x^2(1-x)[/math] .

2. Так как [math]f(x)=-x,

varphi_0(x)equiv 0[/math] , то система (7.20) имеет вид

Итак, имеем линейную систему относительно [math]a_1[/math] и [math]a_2colon[/math]

Приближенное решение задачи: [math]widehat_2(x)=0,!1875419x(1-x)+ 0,!1694707x^2(1-x).[/math] .

Решим задачу методом Галеркина.

1. Пусть сначала [math]m=1[/math] . Решение ищется в форме [math]widehat_1(x)= a_1cdot x(1-x)[/math] .

2. Тогда система (7.24) преобразуется к виду

Так как [math]varphi_1(x)= x(1-x),

Lvarphi_1(x)= varphi»_1(x)+ varphi_1(x)=-2+x(1-x)[/math] , получаем

После вычисления интегралов имеем уравнение [math]-frac,a_1=-frac[/math] , откуда [math]a_1=frac[/math] .

3. Приближенное решение краевой задачи: [math]widehat_1(x)=frac,x(1-x)[/math] . Пусть теперь [math]m=2[/math] .

1. Решение краевой задачи ищется в форме [math]widehat_2(x)=a_1cdot x(1-x)+ a_2cdot x^2(1-x)[/math] .

2. Тогда система (7.24) имеет вид

Вычисляя интегралы, находим

3. Приближенное решение краевой задачи: [math]widehat_2(x)= x(1-x)! left(frac+ frac,xright)[/math] .

Сопоставим полученные решения с точным (табл. 7.2).

7.2>>\hline x& y_<text>& y_<text>& y_<text>& text \hline 0,!25& 0,!045& 0,!04311& 0,!0440& 0,!044014 \hline 0,!50& 0,!071& 0,!06807& 0,!0698& 0,!069747 \hline 0,!75& 0,!062& 0,!05899& 0,!0600& 0,!060050 \hline end[/math]

Очевидно, метод Галеркина дал более точный результат.

Пример 7.4. Найти приближенное решение краевой задачи [math]y»+2xy’-2y=2x^2,

0 leqslant x leqslant 1,[/math] [math]y'(0)=-2,

y(1)+y'(1)=0[/math] методом Галеркина.

В поставленной задаче

1. Зададим [math]m=2[/math] и подберем функции [math]varphi_0(x),, varphi_1(x),, varphi_2(x)[/math] , используя систему [math]1,x,x^2,ldots[/math] . Функция [math]varphi_0(x)[/math] должна удовлетворять условиям (7.12):

Пусть [math]varphi_0(x)=b+cx[/math] , где [math]b,,c[/math] — неопределенные коэффициенты. Тогда

Отсюда [math]b=4[/math] и [math]varphi_0(x)=4-2x[/math] .

Функции [math]varphi_1(x),, varphi_2(x)[/math] должны удовлетворять условиям (7.13):

Первое условие выполняется для функций вида [math]varphi_= x^+b_[/math] . Значения [math]b_[/math] находятся из второго условия [math]1+b_+j+1=0[/math] , откуда [math]b_=-j-2[/math] . Тогда получаем [math]varphi_1(x)=x^2-3,

Таким образом, решение краевой задачи ищется в форме

2. Тогда система (7.24) имеет вид

3. Приближенное решение краевой задачи [math]widehat_2(x)= x^2-2x+1[/math] .

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Методы сведения краевой задачи к задаче Коши

Метод стрельбы. Суть этого метода заключается в сведении решения краевой задачи к многократному решению задачи Коши. Принцип построения метода стрельбы рассмотрим на примере нелинейной краевой задачи:

где [math]f(x,y,y’)[/math] — нелинейная функция, обусловливающая нелинейность дифференциального уравнения (7.25).

При введении новой переменой [math]z=y'[/math] уравнение (7.25) записывается в нормальной форме Коши, а краевые условия видоизменяются:

где [math]eta=y'(a)=operatornamealpha[/math] — параметр, равный тангенсу угла наклона интегральной кривой в точке [math]x=a[/math] . Угол [math]alpha[/math] (параметр [math]eta[/math] ) в процессе многократного решения краевой задачи должен принять такое значение, чтобы интегральная кривая «попала в цель», т.е. в точку [math](b,B)[/math] (рис.7.2 ,а). В общем случае полученное при некотором значении [math]eta[/math] решение [math]y(x,eta)[/math] не будет удовлетворять условию [math]y(b,eta)=B[/math] на правом конце отрезка.

Следовательно, требуется найти такое значение параметра [math]eta[/math] , чтобы оно было корнем нелинейного уравнения [math]Phi(eta)= y(b,n)-B=0[/math] . Для решения этого уравнения, как правило, используются методы половинного деления или секущих. В случае использования метода половинного деления сначала делают «пробные» выстрелы при выбранных наугад или в соответствии с некоторым алгоритмом значениях [math]eta[/math] до тех пор, пока среди значений [math]Phi(eta)[/math] не окажется двух противоположных по знаку. Им соответствует начальный интервал неопределенности, который далее последовательно сокращается путем деления пополам. При применении метода секущих используется формула

где [math]eta^,,eta^[/math] — начальные значения параметра, [math]k[/math] — номер итерации. Итерации прекращаются при выполнении условия окончания [math]bigl|Phi(eta^)bigr| leqslant varepsilon[/math] или [math]bigl|eta^-eta^bigr| leqslant varepsilon[/math] с некоторым положительным [math]varepsilon[/math] , характеризующим точность решения задачи.

Замечание. Точность решения краевой задачи зависит не только от точности определения параметра [math]eta[/math] , но также и от точности решения соответствующей задачи Коши. Поэтому одновременно с уточнением параметра [math]eta[/math] рекомендуется уменьшать шаг при решении задачи Коши, либо выбирать более точный метод.

Рассмотрим применение метода стрельбы для решения линейной краевой задачи (7.3),(7.4):

Видео:Самый сложный элемент в настольном теннисе. Обучение. Срезка или подрезка справа.#настольныйтеннисСкачать

Системы уравнений с частными производными. Характеристики

Для решения систем уравнений с частными производными первого порядка могут быть использованы различные разностные схемы метода сеток, разработанные для одного уравнения. С этой целью формально систему уравнений можно записать в векторной форме с помощью одного уравнения, и тогда вид разностных формул сохраняется таким же, как и для скалярного уравнения. Разница состоит в том, что вместо скалярной сеточной функции вводится векторная.

Рассмотрим систему двух квазилинейных уравнений относительно искомых функций :

(2.60)

Коэффициенты этой системы переменные и зависят от х, t, U, V. Введем следующие обозначения: U — искомый вектор; F — вектор правой части; А, В — матрицы коэффициентов:

Запишем систему уравнений (2.60) в векторном виде:

Для решения этого квазилинейного векторного уравнения могут быть использованы различные разностные схемы, которые применяются для решения одного уравнения.

Мы не будем повторять сказанное ранее для одного уравнения, а остановимся на одном частном случае системы (2.60), важном для приложений. Речь идет о системах гиперболического типа. Введем матрицу С где α, β — некоторые числа. Тогда определитель этой матрицы

(2.61)

является квадратичной формой относительно α и β,т.е.

(2.62)

где коэффициенты q1, q2, q3, легко выразить через элементы матриц А, В, раскрывая определитель (2.61).

Система уравнений с частными производными первого порядка (2.60) называется гиперболической,если квадратичная форма (2.62) разлагается на вещественные линейные множители:

причем векторы неколлинеарны. Эти векторы в каждой точке плоскости (х,t) образуют два направления, которые называются характеристическими. Линия, касательная к которой в каждой точке имеет характеристическое направление, называется характеристикой. Через каждую точку проходят две характеристики, соответствующие двум характеристическим направлениям. Таким образом, всю плоскость (х, t) можно покрыть двумя семействами характеристик (рис. 2.18).

Рис. 2.18. Характеристики

Заметим, что в случае системы уравнений (2.60) с постоянными коэффициентами характеристические направления, если они существуют, постоянны для всех точек плоскости. Им соответствуют два семейства прямолинейных характеристик. В самом общем случае, когда коэффициенты системы (2.60) зависят от х, t, U, V, характеристики могут существовать в одной части плоскости (х, t) и отсутствовать в другой. Следовательно, гиперболичность системы (2.60) может быть не на всей плоскости, а лишь в некоторой области.

Наряду с гиперболическими системами существуют также параболические (с одним семейством характеристик) и эллиптические (действительных характеристик нет) системы.

Характеристики можно использовать для построения алгоритма численного решения системы уравнений с частными производными в области ее гиперболичности. Такой способ решения называется методом характеристик.

Не приводя подробных выкладок и опуская сами формулы, изложим идею метода характеристик. Рассмотрим задачу Коши. Пусть при t = 0 заданы начальные значения функций . Выбираем любой отрезок [а,b] на оси х и разбиваем его на части точками (рис. 2.19). В данном случае принято n= 4.

Рис. 2.19. К решению задачи Коши методом характеристик

Из точки А0 проводим характеристику первого семейства, из А1 — второго. Находим точку пересечения В0. Используя некоторые соотношения (характеристические) вдоль отрезков характеристик А0В0 и А1В0,заменяющие исходные уравнения, вычисляем искомые функции в точке В0. Аналогично находим решение в других точках слоя В. При этом в отличие от метода сеток этот слой не является прямолинейным отрезком t= const, а определяется точками пересечения характеристик.

Далее вычисляем искомые значения в точках слоев С, Dи т.д. При этом каждый раз (при решении задачи Коши) при переходе от слоя к слою число узлов уменьшается на единицу, так что на последнем слое получается лишь один узел. Область решения задачи Коши представляет собой криволинейный треугольник с кусочно гладкими сторонами.

При решении краевой задачи используют значения искомых функций на границах. В этом случае расчетная область изменяется: она прилегает к границе х = const, на которой заданы значения функций U(x), V(x). При этом вблизи границы используют характеристики одного семейства, выходящие из границы и попадающие в расчетную область. Если граничные условия задают при двух значениях х, то алгоритм метода характеристик значительно усложняется.

Достоинством метода характеристик является то, что он основан на физической сущности задачи, поскольку возмущения распространяются по характеристикам. Метод позволяет выявить разрывы в решении. Недостатком метода является нерегулярность получаемой сетки, поскольку узлы располагаются неравномерно (в точках пересечения характеристик).

Для устранения этого недостатка разработаны так называемые сеточно-характеристические методы. Их идея состоит в том, что сетка фиксируется заранее, а характеристики проводятся «назад» из узлов (j+ 1)-ого слоя до пересечения с j-ым слоем. Значения U, Vв точках пересечения вычисляются путем интерполяции по ранее найденному решению в узлах j-ого слоя.

Геометрическая интерпретация сеточно-характеристического метода показана на рис. 2.20. Здесь точками отмечены заранее выбранные узлы; штриховые линии — отрезки характеристик. Значения функций в точках пересечения А и В находятся интерполированием решения в узлах и Эти значения используют для определения решения в расчетном узле (i, j+1).

Рис. 2.20. Геометрическая интерпретация сеточно-характеристического метода

🎥 Видео

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

1. Уравнения в частных производных первого порядка (уравнения переноса)Скачать

Линейные дифференциальные уравнения в частных производныхСкачать

Ali Riyaziyyat Dərs 70(Birinci və ikinci tərtib xüsusi törəməli diferensial tənliklər)Скачать

Сарсимбаева С.М. Численные методы анализа и алгебры. Лекция 14-15. (Метод сеток).Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Найти общее решение уравнения в частных производных первого порядка.Скачать

2. Приведение уравнений второго порядка к каноническому видуСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Решение уравнений в частных производныхСкачать

Приведение уравнений в частных производных к безразмерному виду.Скачать