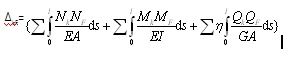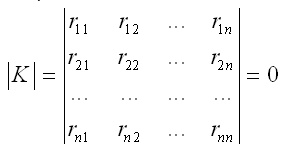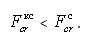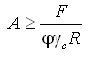Уравнение устойчивости на основе метода перемещений

Главное меню

Присоединяйтесь

Видео:основная система и канонические уравнения метода перемещенийСкачать

Устойчивость рам

Расчет на устойчивость деформируемых систем проводится в основном методом перемещений с помощью ЭВМ. В основе метода перемещений при расчете стержневых систем на устойчивость лежит дифференциальное уравнение изгиба сжатого прямолинейного стержня постоянного сечения.

Предварительно необходимо выполнить статический расчет сооружения, целью которого является определение перемещений узлов сооружения и внутренних сил в его элементах.

Внешние нагрузки исходного состояния, вызвавшие продольные силы, в дальнейшем расчете не участвуют.

Основная система и основные неизвестные метода перемещений выбираются в обычном порядке. Т.к., дополнительные узловые нагрузки при исследовании устойчивости полагаются нулевыми, то канонические уравнения метода перемещений принимают вид:

где R – матрица мгновенной жесткости, элементы которой, реакции r_ik во введенных дополнительных связях, зависят от продольных сил в стержнях системы.

Расчет элементов матрицы мгновенной жесткости осуществляется как и в методе перемещений. Основная особенность метода перемещений в расчетах на устойчивость состоит в том, что в сжатых стержнях эпюры изгибающих моментов от единичных перемещений получаются криволинейными за счет дополнительного изгибающего действия продольных сил. А выражения для вычисления реакций в опорах сжатых стержней содержат поправочные множители в виде специальных функций от безразмерных параметров ν.

В несжатых стержнях построение единичных эпюр изгибающих моментов и вычисление реакций выполняется в обычном порядке.

Следовательно, коэффициенты канонических уравнений метода перемещений зависят от безразмерных параметров ν:

Критическим состояниям равновесия отвечают ненулевые перемещения узлов деформируемой системы:

Это возможно, если определитель матрицы мгновенной жесткости равен нулю, что и соответствует моменту потери устойчивости:

Раскрытие определителя приводит к уравнению, называемому уравнением устойчивости.

Дальнейшее решение задачи состоит в определении значений нагрузок на раму, удовлетворяющих уравнению устойчивости. Наименьшая из них является критической нагрузкой.

Критическое значение сжимающей силы определяется по формуле:

Критерием глобальной устойчивости сооружения является положительная определенность матрицы мгновенной жесткости деформированной системы:

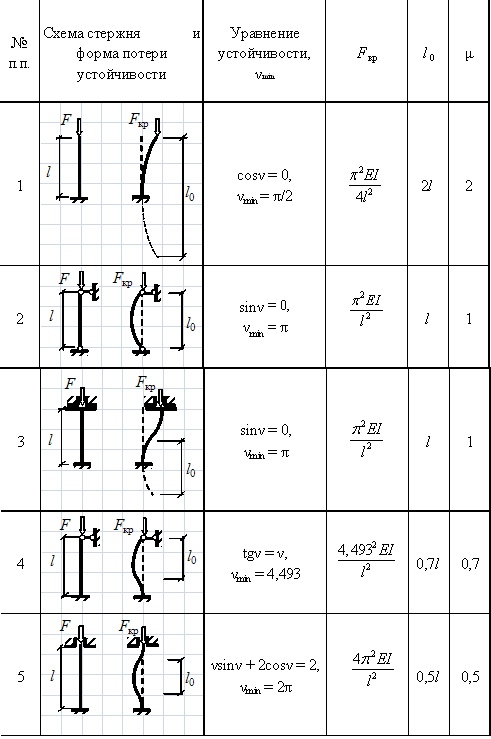
Таблица эпюр изгибающих моментов и реакций для прямых сжатых балок с разными условиями закрепления и значения специальных функций в зависимости от безразмерных параметров ν :

Видео:Расчет на устойчивость методом перемещений ( угловое перемещение)Скачать

Методические указания к расчетно-графической работе “Расчет рамно-балочных систем на устойчивость”

Министерство образования и науки

Казанский государственный архитектурно-строительный университет

Кафедра строительной механики

Видео:Расчет рамы на устойчивость методом перемещений. Строительная механика.Скачать

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к расчетно-графической работе

“Расчет рамно-балочных систем

Ш17 Методические указания к расчетно-графической работе “Расчет рамно-балочных систем на устойчивость” / Шакирзянов, . – Казань: КГАСУ, 2011. – 16 с.

Печатается по решению редакционно-издательского совета Казан-ского государственного архитектурно-строительного университета.

Методические указания предназначены для успешного усвоения теоретических знаний, закрепления навыков по расчету сооружений на устойчивость и выполнения расчетно-графической работы (РГР) по устойчивости сооружений.

Определяются общая схема и последовательность выполнения РГР, даются рекомендации для ее самостоятельного выполнения и примеры решения задач расчета рамно-балочных систем на устойчивость методом перемещений.

Кандидат физико-математических наук, профессор кафедры теоретической механики КГАСУ

Ó Казанский государственный

Строительная механика − это наука о принципах и методах расчета сооружений на прочность, жесткость и устойчивость. Поэтому бакалавры и магистры, обучающиеся по направлению “Строительство” и изучающие курс строительной механики, а также аспиранты и специалисты-строители, повышающие квалификацию по этому направлению должны знать теоретические положения, принципы и методы расчета сооружений на устойчивость.

Под воздействием внешней нагрузки в рамно-балочных системах (рис. 1 а) могут возникать большие продольные усилия (рис. 1 б), приводящие к потере устойчивости системы. В таких случаях (рис. 1 в), а также при узловом воздействии нагрузки (рис. 1 г) может ставиться задача проверки этих систем на устойчивость.

Обе эти задачи можно решать методом перемещений по единой методике, если принять упрощающие гипотезы:

– нагрузка прикладывается только в узлах;

– продольные силы вызывают только центральное сжатие;

– при потере устойчивости напряжения остаются в упругой зоне;

– деформации малы и расстояния между узлами сохраняются.

Алгоритм расчета на устойчивость методом перемещений

1. Определение числа неизвестных.

2. Выбор основной системы.

3. Построение эпюры продольных сил N0 в основной системе.

4. Определение параметров устойчивости стержней

.

Все параметры устойчивости необходимо выразить через максимальный из них и обозначить v=max vi , а остальные определить как , где коэффициенты .

5. Запись канонических уравнений.

6. Рассмотрение единичных состояний основной системы.

7. Построение эпюр изгибающих моментов в единичных состояниях.

8. Определение коэффициентов канонических уравнений.

9. Решение уравнения устойчивости .

10. Определение критических сил и приведенных длин сжатых стержней по формулам

, .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. На одноэтажную раму действует сосредоточенная сила, направленная вдоль оси одной из стоек (рис. 2 а). Определить величину этой силы, при которой рама достигает критического состояния.

1. Определяем число неизвестных по методу перемещений:

2. Выбираем основную систему (рис. 2 б).

3. Строим эпюру продольных сил в основной системе (рис. 2 в).

4. Параметры устойчивости стержней:

, .

5. Каноническое уравнение будет

(так внешняя нагрузка до момента потери устойчивости не вызывает изгиба элементов, то ).

6. Рассмотрим единичное состояние основной системы (рис. 3 а).

7. В единичном состоянии строим эпюру изгибающих моментов. При этом надо помнить следующее: в стержне 3 в основной системе имеется сжимающие усилие (рис. 2 в), поэтому при построении эпюры изгибающих моментов в этом стержне надо пользоваться специальной таблицей метода перемещений (табл. 2 в приложении), а в стержнях 1 и 2 сжимающие силы отсутствуют, поэтому при построении эпюр моментов в этих стержнях надо использовать обычную таблицу метода перемещений (табл. 3). Тогда эпюра моментов для стержня 3 будет криволинейной, а для стержня 1 будет прямолинейной (рис. 3 б). Следует отметить, что в данной задаче построение этой эпюры не обязательно.

8. По рис. 3 в определяем коэффициент канонического уравнения:

.

9. Каноническое уравнение имеет два решения:

1) , 2) .

Согласно основной системе (рис. 2 б), второе решение соответствует закреплению 3-го стержня в горизонтальном направлении. Поэтому этот стержень, подвергнутый воздействию сжимающей силы P, можно рассматривать отдельно (рис. 3 г).

Такие задачи решаются теоретически, результаты их расчета приведены в приложении в табл. 1. Нашему случаю соответствует 4-ая схема этой таблицы, из которого определяем коэффициент приведенной длины стержня μ=0,7. Тогда

.

Если рассматривать первое решение, то

.

Из него получаем уравнение или .

Тогда, используя табл. 4, определяем корень уравнения .

Итак, получили два решения: 1) , 2) . По критерию Эйлера, критической является наименьшая из них. Поэтому .

10. Определяем величину критической силы и коэффициент приведенной длины стержня. Принимая

,

, .

Как видно из данного примера, уравнение дает завышенное значение приведенной длины стержня (а значит и критической силы). При решении других задач получаются аналогичные результаты. Поэтому в дальнейшем решения типа рассматривать не будем.

Задача 2. Провести расчет рамы, представленной на рис. 4 а, на устойчивость методом перемещений.

1. Определяем число неизвестных по методу перемещений:

2. Выберем основную систему (ОС). Она получается введением двух условных связей − заделки и опоры (рис. 4 б).

3. Строим эпюру продольных сил в основной системе (рис. 4 в). В ней имеются два стержня, в которых есть сжимающие продольные усилия.

4. Параметры устойчивости стержней рамы будут:

, , .

Наибольший из них соответствует 1-му стержню. Поэтому примем его параметр устойчивости за основной и обозначим

.

,

имеем .

5. Запишем систему канонических уравнений:

Эта однородная система уравнений имеет два решения:

1) 2) .

Второе решение, как дающее завышенное значение критического корня, рассматривать не будем. А первое решение с учетом принимает вид

.

Это и есть уравнение устойчивости.

6. Рассмотрим два единичных состояния основной системы, в которых обозначим деформации элементов и реактивные усилия (рис. 5):

7. Используя таблицы метода перемещений, в обоих состояниях строим эпюры изгибающих моментов (рис. 6 а, б).

При этом при построении эпюр в стержнях 1 и 2 (в них учитывается сжатие) основной системы используем специальную таблицу метода перемещений (табл. 2), а при построении эпюр в стержнях 3 и 4 (где сжимающие силы отсутствуют) используем обычную таблицу метода перемещений (табл. 3). Поэтому эпюры моментов для стержней 1 и 2 них будут криволинейными, а для стержней 3 и 4 − прямолинейными.

8. Коэффициенты системы канонических уравнений определяем согласно единичным состояниям (рис. 5) и по рис. 6 а, б:

;

;

9. Решаем уравнение устойчивости. Для этого подставим найденные коэффициенты в уравнение устойчивости и сократим его на EI. Получим трансцендентное уравнение (уравнение с бесконечным числом корней). С целью определения наименьшего положительного корня этого уравнения вначале определим интервал, в котором этот корень находится. Для этого проведем следующие рассуждения:

1) уравнение устойчивости зависит от параметра устойчивости 1-го стержня рамы , поэтому исследуем поведение этого стержня;

2) в состоянии “малой жесткости” рамы, когда изгибные жесткости всех стержней (кроме 1-го) равны нулю (рис. 7 а), стержень 1 можно рассматривать отдельно как показано на рис. 7 б. В этом случае по табл. 1 имеем . Тогда ;

3) в состоянии “большой жесткости”, когда изгибные жесткости всех стержней (кроме 1-го) равны бесконечности (рис. 7 в), стержень 1 можно рассматривать отдельно как показано на рис. 7 г. По табл. 1 принимаем . Тогда, ;

4) в действительности жесткость 1-го стержня находится в интервале от нуля до бесконечности. Следовательно, искомый корень уравнения устойчивости находится между найденными крайними величинами, т. е.

.

Теперь уточним его. Это удобно проводить в следующей табличной форме (значения специальных функций берутся из табл. 4):

Видео:С.М. Задача №8.1 расчёт рамы на устойчивость методом перемещенийСкачать

Уравнение устойчивости на основе метода перемещений

114) Что представляют собой дополнительные связи основной системы метода перемещений?

Линейные связи по направлению линейных смещений и плавающие заделки по направлению поворота жёстких узлов.

115) Как вводятся дополнительные угловые связи при получении основной системы метода перемещений?

Определяется степень кинематической неопределимости, узлы, способные к повороту, и в эти места вводится плавающая заделка. (n_у)

116) Как вводятся дополнительные линейные связи при получении основной системы метода перемещений?

Определяется степень кинематической неопределимости, узлы, способные к линейным перемещениям, и в эти места вводятся линейные связи по направлению перемещения. (n_л)

117) Каким требованиям должна удовлетворять основная система метода перемещений?

Все узлы становятся неподвижными, каждый стержень представляет собой простую статически определимую балку.

118) Сформулируйте физический смысл канонических уравнений метода перемещений?

Сумма реакций в дополнительных связях от смещения этих связей и внешнего воздействия равна нулю.

119) Какими особенностями обладает система канонических уравнений метода перемещений?

Порядок системы равен степени кинематической неопределимости. В системе канонических уравнений коэффициенты при неизвест­ных с одинаковыми индексами называются главными коэффициентами, и они всегда положительны r_ii > 0. Остальные коэффициенты называются побочными, и для них выполняется теорема о взаимности воз­можных реакций r_ik = r_ki. Размерности коэффициентов при неизвестных и свободных членов сис­темы канонических уравнений легко определяются на основании их статического смысла, сформулированного выше.

120) Что представляют собой коэффициенты при неизвестных системы канонических уравнений метода перемещений?

Реакция в связи i от единичного смещения связи k.

121) Что представляют собой свободные члены системы канонических уравнений метода перемещений?

Реакции в введённых дополнительных угловых связях и в линейных от действующей нагрузки.

122) Какая теорема строительной механики используется при определении коэффициентов при неизвестных системы канонических уравнений метода перемещений?

Теорема о взаимности возможных реакций r_ik = r_ki.

123) Какие размерности могут иметь коэффициенты при неизвестных системы канонических уравнений метода перемещений?

(кН*м)/рад; кН; кН/рад; кН/м

124) Какие размерности могут иметь свободные члены системы канонических уравнений метода перемещений?

125) Какими особенностями обладают стержни основной системы метода перемещений?

Каждый стержень представляет собой простую статически определимую балку.

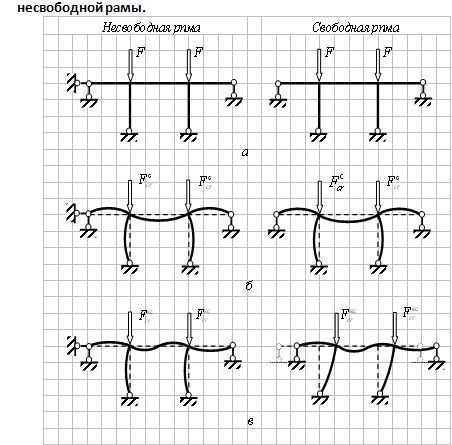
126) Что понимают под термином «свободные» и» несвободные» рамы?

Свободная рама — рама, которая не закреплена от линейных смещений. Несвободная — закреплена.

127) Как получить эпюру изгибающих моментов в заданной схеме на основе метода перемещений?

на основании принципа независимости действия сил.

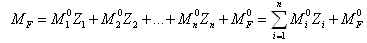
128) Как определяются знаки реакций в дополнительных связях основной системы метода перемещений?

Реакция считается положительной, если они её направление совпадает с направлением задаваемого перемещения.

129) Как определяются реакции в дополнительных связях основной системы метода перемещений?

Способом сечений и вырезанием узлов.

130) Как определяются реакции в дополнительных линейных связях основной системы метода перемещений?

Способом сечений, которые проводят параллельно оси связи через все стержни схемы, деформируемые при принудительном смещении этой связи.

131) Как определяются реакции в дополнительных угловых связях основной системы метода перемещений?

Из условия равновесия узла, в который введена дополнительная связь.

132) Как определяются усилия в стержнях основной системы метода перемещений от действия внешней нагрузки?

По таблице в зависимости от типа закрепления и вида нагрузки.

133) Как определяются усилия в стержнях основной системы метода перемещений от смещения дополнительных связей?

По таблице, с учетом заданного перемещения и соответствующей ему деформационной схемы.

134) В каких случаях действия внешней нагрузки усилия от нее в стержнях основной системы метода перемещений будут нулевыми?

При действии узловых нагрузок.

135) Что принимают за неизвестные при расчете методом перемещений?

Реакции в дополнительных связях.

136) Какую последовательность расчета необходимо соблюсти, чтобы получить систему канонических уравнений метода перемещений в численном виде?

Определить степень кинематической неопределимости, выбрать О.С.М.П., записать систему канонических уравнений в общем виде, рассмотреть её состояния, построить эпюры, рассмотреть равновесие узлов (или сечения), найти коэффициенты и свободные члены.

137) Как получить эпюру поперечных сил в заданной статически неопределимой системе, если получена эпюра изгибающих моментов?

Смотри метод сил.

138) Как получить эпюру продольных сил, если получена эпюра поперечных сил?

Смотри метод сил (условие равновесия узлов).

139) На каком этапе расчета методом перемещений учитываются внешние узловые нагрузки?

В методе сечений; при подсчёте продольных сил.

140) Как производятся проверки расчета методом перемещений?

По эпюре моментов проверяют жёсткие узлы, статическая проверка, деформационная.

141) Как по построенным эпюрам усилий определить опорные реакции?

Подставить значения эпюр в соответствующие опорные реакции, соблюдая направление. Значение эпюры, – есть значение опорных реакций. Направление, – по правилу знаков.

142) Как определяются усилия в стержнях основной системы метода перемещений?

По таблицам реакций и усилий.

143) В каких случаях можно использовать основную систему метода перемещений без постановки дополнительных линейных связей?

В случае, если в стойках поперечные силы могут быть определены непосредственно из уравнения равновесия ∑x = 0.

144) Какими особенностями обладает основная система метода перемещений без постановки дополнительных линейных связей?

В стойках поперечные силы могут быть определены непосредственно из уравнения равновесия ∑x = 0, понижение порядка канонических уравнений, при расчёте стержней применяются дополнительные таблицы реакций для стержней двух типов, учитывающие смещение «плавающих» заделок при повороте самой связи и действии внешней нагрузки.

145) Сформулируйте особенности построения эпюр усилий в стержнях основной системы метода перемещений без дополнительных линейных связей, имеющих линейные смещения, при задании единичных углов поворота дополнительным угловым связям.

Так как дополнительных линейных связей мы не ставим, следовательно, при расчёте стержней применяются дополнительные таблицы реакций, учитывающие смещение «плавающих» заделок при повороте самой связи.

147) Сформулируйте особенности построения эпюр усилий в стержнях основной системы метода перемещений без дополнительных линейных связей, имеющих линейные смещения, при действии внешней нагрузки.

Так как дополнительных линейных связей мы не ставим, следовательно, при расчёте стержней применяются дополнительные таблицы реакций, учитывающие смещение «плавающих» заделок при действии внешней нагрузки. Для горизонтально загруженных стержней основной системы эпюра М_F 0 строится по старым таблицам, для вертикальных — по новым с учётом вышележащих горизонтальных нагрузок.

148) Какие упрощения возможны при расчете методом перемещений симметричных расчетных схем?

Способом группировки представить углы поворота связей как сумму и разность двух неизвестных. Или с помощью способа разложения нагрузки и с учётом свойства 1 рассматривать только симметричную часть.

149) Сформулируйте принципы определения перемещений в статически неопределимых расчетных схемах.

Для определения перемещений в статически неопределимых расчётных схемах одна из эпюр, входящих под знак интеграла Максвелла-Мора, может быть взята в любой статически определимой основной системе метода сил.

150) Что называют потерей устойчивости?

Потеря устойчивости — явление внезапного перехода из одного напряжённо-деформированного состояния в качественно новое.

151) Что такое критическая сила?

Наибольшее значение силы, при которой расчётная схема ещё сохраняет своё первоначальное напряжённо-деформированное состояние, называют критической силой (или критической нагрузкой).

152) Сформулируйте допущения при расчете на устойчивость.

1) Нагрузки считаются только узловые, центральные приложены без эксцентриситета.

2) Материал считают идеально упругим.

3)Местным ослаблением поперечных сечений пренебрегают, т. е. А — брутто.

4) Если на расчётную схему действует несколько сжимающих сил, то соотношение между ними сохраняется и после потери устойчивости.

153) Укажите и сформулируйте типы задач при расчете стержней на устойчивость.

1) Проверка прочности центрально сжатых стержней

2) Определение несущей способности при продольном изгибе

3) Подбор сечения стержня при продольном изгибе

154) Покажите, какие виды потери устойчивости Вы знаете.

См. вопросы 158-162.

155) Что называют расчетной длиной центрально сжатого стержня?

Выражается длиной синусоиды в этой форме потери устойчивости, некоторая условная длина шарнирно опёртого по концам стержня, для которого критическая сила равна критической силе для данного загружения.

156) Что такое Эйлерова критическая сила?

Наименьшее значение критической силы для шарнирно опертого стержня .

157) Как зависит значение критической силы от типа закрепления концов центрально сжатого стержня.

Чем жёстче защемлён стержень, тем больше критическая сила.

158) Покажите значение критической силы и расчетную длину для стержня с двумя защемленными концами.

159) Покажите значение критической силы и расчетную длину для стержня с защемленным и шарнирным концами.

160) Покажите значение критической силы и расчетную длину для стержня с защемленным и свободным концами.

161) Покажите значение критической силы и расчетную длину для стержня с двумя шарнирными концами.

162) Покажите значение критической силы и расчетную длину для стержня, у которого один конец защемлен жестко, а защемление на другом конце имеет подвижность перпендикулярно оси стержня.

163) Сформулируйте принцип статического способа для определения критической силы.

Рассматривают новое равновесное состояние после потери устойчивости, из которого и находят величины критической нагрузки. Для изгибаемых стержней этот способ — метод непосредственного интегрирования оси статически изогнутого стержня.

164) Как записывается уравнение устойчивости для расчетной схемы на основе метода перемещений?

Определитель, состоящий из коэффициентов при неизвестных, равный 0.

165) Какие упрощения возможны при расчете на устойчивость методом перемещений симметричных рам?

Без постановки линейных связей + учёт симметрии.

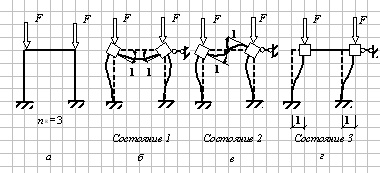
166) Какие формы потери устойчивости возможны в симметричных расчетных схемах?

Могут быть симметричные и кососимметричные формы потери устойчивости.

167) Покажите примеры потери устойчивости симметричной свободной рамы.

168) Покажите примеры потери устойчивости симметричной несвободной рамы.

169) При какой форме потери устойчивости симметричной свободной рамы критические силы будут наименьшими?

2. для свободных рам

170) При какой форме потери устойчивости симметричной несвободной рамы критические силы будут наименьшими?

1. для несвободных рам Напряжение, возникающее в стержне при приложении к нему критической силы: ,где – радиус инерции поперечного сечения стержня, λ = l₀/i – гибкость стержня.

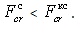
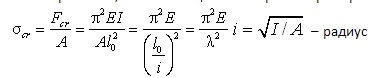
172) Что называют коэффициентом продольного изгиба?

φ — учитывает возможность появления продольного изгиба в стержне, определяет степень снижения расчётного сопротивления материала при продольном изгибе.

173) Что такое гибкость стержня?

λ = l₀/i, где l₀ — расчётная длина центрально сжатого стержня, i — радиус сечения

174) Сформулируйте пределы применимости формулы Эйлера.

При λ >λ_cr для определения критических напряжений и, следовательно, и критических сил можно пользоваться формулой Эйлера

175) В каких случаях при определении критического напряжения используется формула Ясинского?

В случае, если λ 2 , где a, b и c – экспериментально определяемые коэффициенты, зависящие от материала

176) Как определить допускаемую нагрузку при расчете устойчивость?

177) Как подобрать сечение стержня при продольном изгибе?

178) Как проверить работу центрально сжатых стержней на устойчивость?

💡 Видео

Основная система метода перемещенийСкачать

расчет рамы на устойчивость методом перемещений (линейное перемещение) / строительная механикаСкачать

Метод перемещений: степень кинематической неопределимостиСкачать

Устойчивость. Метод перемещений - 2.Скачать

С.М. Тема №8 Расчёт на устойчивость методом перемещенийСкачать

Расчет рамы методом перемещенийСкачать

Расчет плоских статически неопределимых рам на устойчивость методом перемещений (1 часть)Скачать

Метод перемещений. Линейное перемещениеСкачать

Основы метода перемещенийСкачать

Устойчивость. Лекция 1. ТеорияСкачать

Расчет симметричных систем методом перемещений (ч 1)Скачать

С.М. Задача №8.3 (начало) расчёт рам на устойчивость методом перемещенийСкачать

Метод перемещений Часть 1Скачать

Строительная механика. Расчет рамы методом перемещений. Часть 1.Скачать