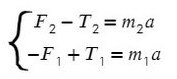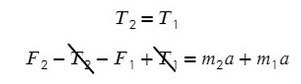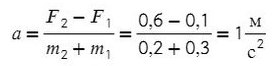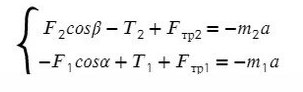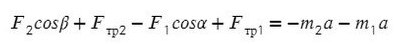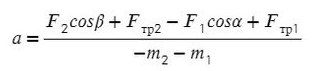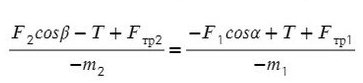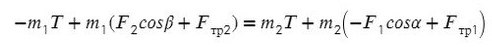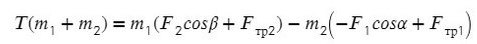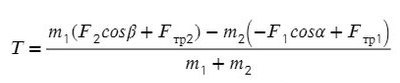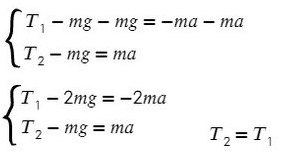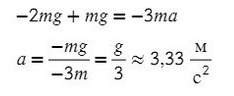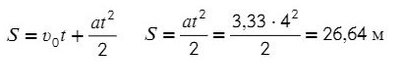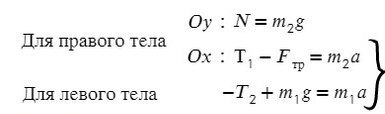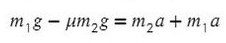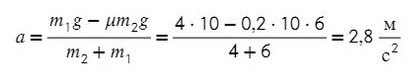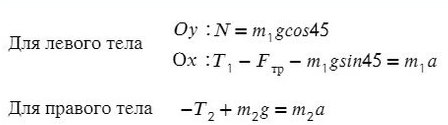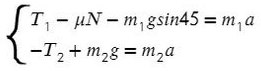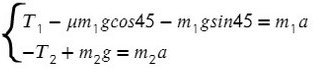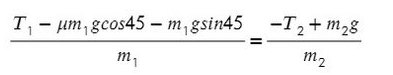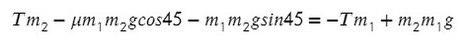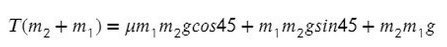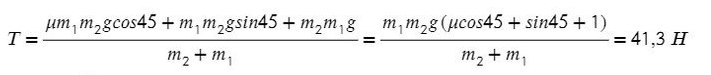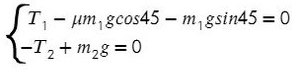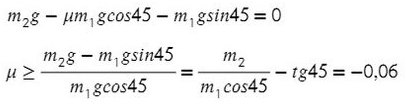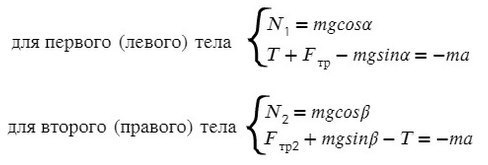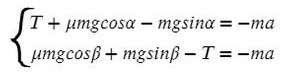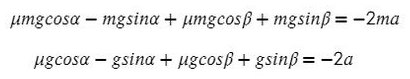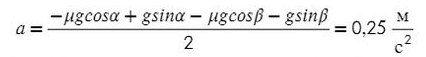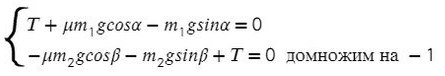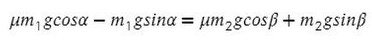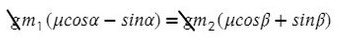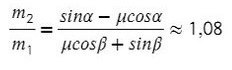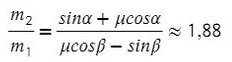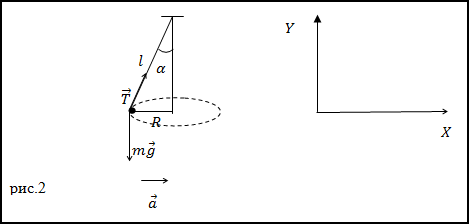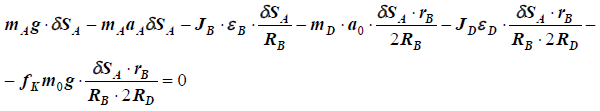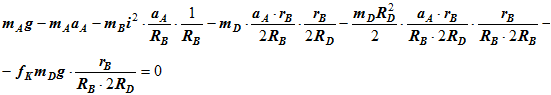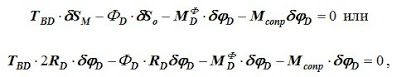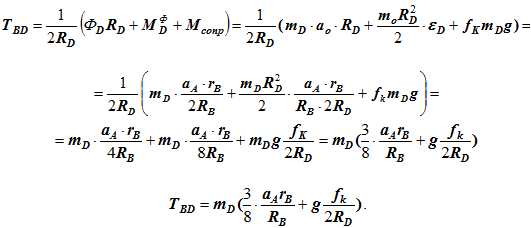Уравнение ускорения и натяжения нити (7 видео)

Уравнение ускорения и натяжения нити

Динамика: движения системы связанных тел.

Проецирование сил нескольких объектов.

Действие второго закона Ньютона на тела, которые скреплены нитью

Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.

А для тех, кто все помнит, поехали!

Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?

Движение происходит только на оси X.

Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.

По II з. Ньютона спроецируем силы обоих тел на Ох:

Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T ₁ и Т ₂.

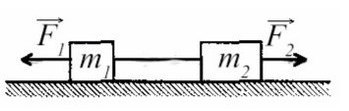
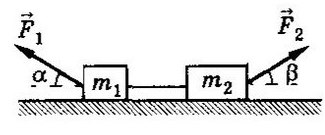
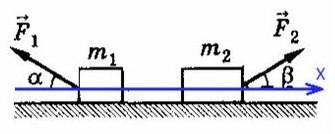
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.

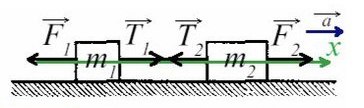
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).

По II з. Ньютона спроецируем силы обоих тел на Ох:

Сложим уравнения и выразим ускорение:

Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:

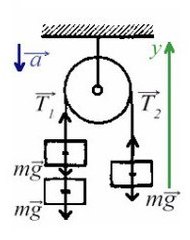
Задача 3 . Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?

В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.

Вычтем из первого уравнения второе:

Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:

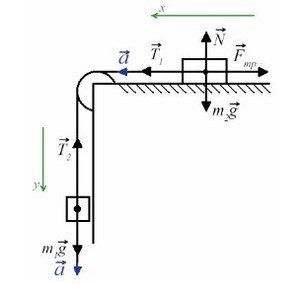
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.

Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):

(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)

Сложим два нижних уравнения для того, чтобы T сократилось:

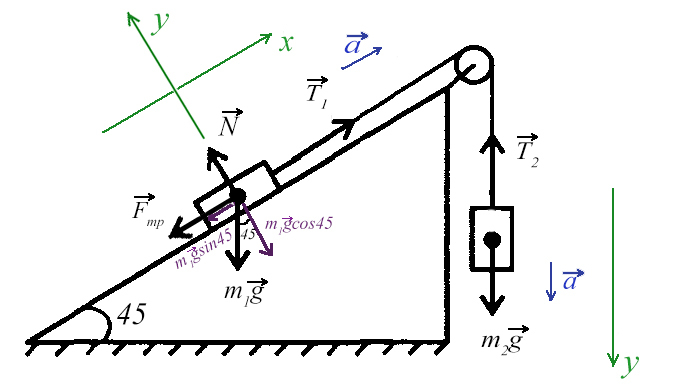
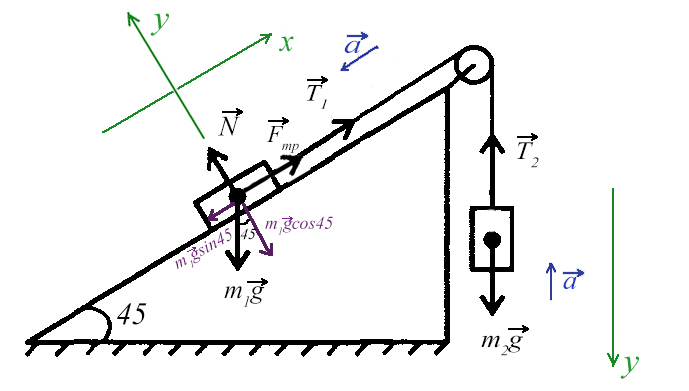
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?

Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.

Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):

Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:

Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:

Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:

Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.

Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.

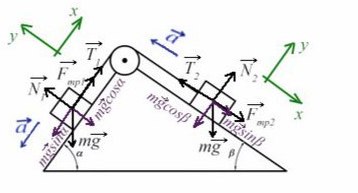
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.

В данной задаче уже потребуются все уравнения на обе оси для каждого тела:

Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:

Сложим уравнения и сократим на массу:

Подставив в любое уравнение найденное ускорение, найдем Т:

А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:

Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:

Получили, что отношение масс должно быть таким:

Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:

Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.

У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.

В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.

Содержание

Формула силы натяжения нити
Определение и формула силы натяжения нити
Единицы измерения силы натяжения нити
Примеры решения задач
iSopromat.ru
Условие задачи
Пример решения
📹 Видео

Видео:Определить ускорение грузов массы m1, m2 и m3, а также силу натяжения нитей: Волькенштейн 2.12*Скачать

Формула силы натяжения нити

Видео:Сила натяжения нити (видео 26) | Силы. Законы Ньютона | ФизикаСкачать

Определение и формула силы натяжения нити

Силу натяжения определяют как равнодействующую сил $(bar)$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar$ и $bar$, и $bar$ . Математически определение для силы натяжения нити можно записать как:

где $bar$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:

где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.

Видео:Урок 315. Решение задач динамикиСкачать

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

Видео:Физика.Решение задач.Выполнялка 1Скачать

Примеры решения задач

Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

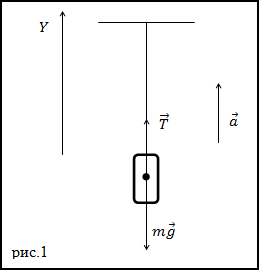
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

где $bar$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:

Из выражения (1.2) получим ускорение:

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

Ответ. a=1,2м/с 2

Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

$$ begin X: quad T sin alpha=m a=m omega^ R(2.2) \ Y: quad-m g+T cos alpha=0 end $$

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

Из рис.2 видно, что:

Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

Видео:Математика это не ИсламСкачать

iSopromat.ru

Пример расчета ускорения груза и натяжения нитей для заданной механической системы, движущейся из состояния покоя, без учета моментов сопротивления в подшипниках и массы нерастяжимых нитей.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Условие задачи

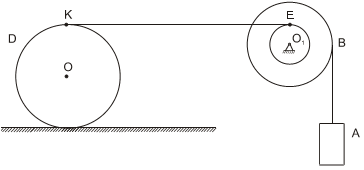
Для заданной механической системы определить ускорение груза и натяжения нитей.

Система движется из состояния покоя, моменты сопротивления в подшипниках не учитывать, массами нитей пренебречь, нити не растяжимы (рис. 2.1).

Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Пример решения

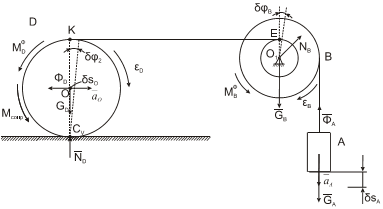
Определим направление движения системы, указав направление ускорения груза A, покажем на рис. 2.2. задаваемые силы: G_A, G_B, G_D реакции связей N_B, N_D (направление N_B пока неизвестно). Силы инерции для тела A приводятся к главному вектору сил инерции Ф_А=m_A∙a_A, для тела B к главному моменту сил инерции M_B Ф =J_B∙ε_B, для тела D, совершающего плоское движение к главному вектору сил инерции Ф_D=m_D∙a_D и к главному моменту сил инерции M_D Ф =J_D∙ε_D. Коэффициент трения качения определяет наличие момента сопротивления

Ускорения и перемещения точек системы получаются дифференцированием и интегрированием зависимостей между линейными и угловыми скоростями точек системы.

Приняв скорость груза V_A, получим соотношения

Можно продифференцировать и проинтегрировать выше приведенные формулы и получить выражения

Сообщим системе возможное перемещение в направлении ее действительного движения. Силы и моменты, действующие на систему, совершат элементарную работу. Сумма всех работ должна быть равна нолю. Момент сопротивления отнесем к внешним воздействиям. Это позволит считать данную систему идеальной. Составим общее уравнение динамики (уравнение работ):

Подставим данные задачи и получим:

Сократив на δS_A — задаваемое нами возможное перемещение груза А получим:

Из этого соотношения определим ускорение груза

Из найденных ранее соотношений можно определить: ε_B, a₀, ε_D.

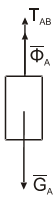
При решении задачи этим методом внутренние силы в уравнения не входят. Для определения натяжения нитей нужно сделать эти силы внешними, для чего разделяем систему на части. Рассмотрим отдельно груз А, на который действуют силы Ф_A, G_A и сила T_AB, ставшая внешней (рис. 2.3). Для этой системы можно написать или принцип Даламбера или общее уравнение динамики.

Находим натяжение нити:

Для определения натяжения нити между телами B и D можно составить общее уравнение динамики (или написать принцип Даламбера) для тела B или D.

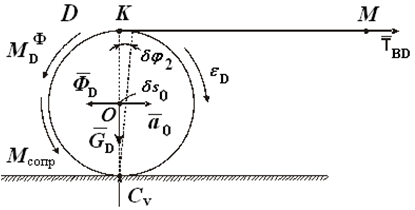
Рассмотрим тело D (рис. 2.4). Покажем действующие внешние силы и силы инерции. Натяжение нити Т_BD стало внешней силой. Приняв за возможное перемещение угол поворота тела D — δφ_D составим уравнение работ.

Для проверки результатов можно написать общее уравнение динамики (или принцип Даламбера) для блока B.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах