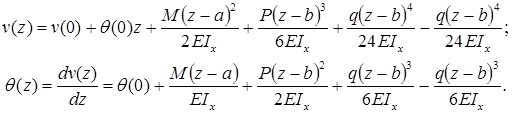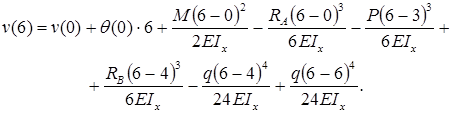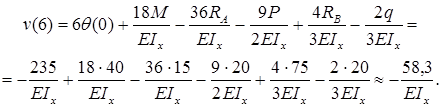Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
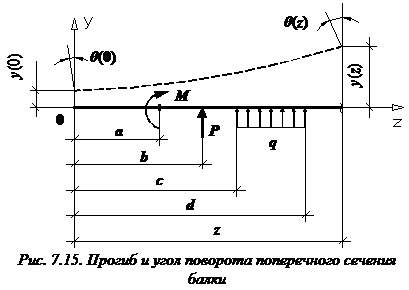
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 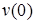
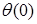
- Уравнение упругой линии балки на примере
- Дифференциальное уравнение упругой линии балки и его интегрирование
- Метод интегрирования дифференциального уравнения изгиба балки
- Консольная балка с силой на конце
- Шарнирно закрепленная балка с силой посередине
- Консольная балка с равномерно распределенной нагрузкой
- 🔍 Видео
Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при 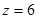
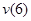
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 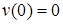
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
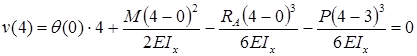
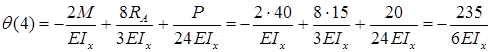
Прогиб консоли при z=6м:
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
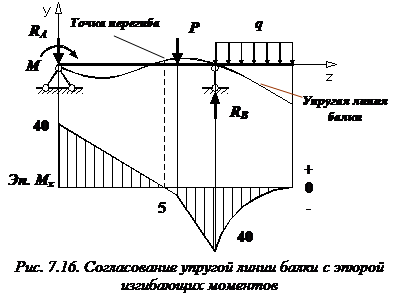
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Дифференциальное уравнение упругой линии балки и его интегрирование
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений

а после второго интегрирования – прогибы балки

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

Метод интегрирования дифференциального уравнения изгиба балки
Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.
$EI,y»(x) = M(x)$ – полученное дифференциальное уравнение;
$EI,y'(x) = EI,varphi (x) = int dx + C$ – первый интеграл (уравнение углов поворота);
$EI,y(x) = int dx = iint dxdx + C,x + D$ – второй интеграл (уравнение прогибов).
Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).
Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI,varphi (0) = C$, а прогиб $EI,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.
Видео:Построение эпюры прогибов балкиСкачать

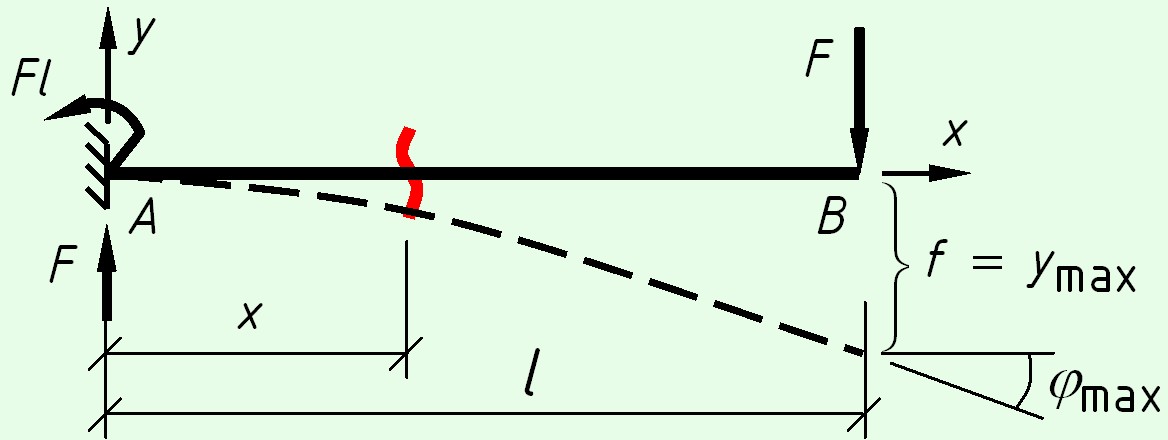
Консольная балка с силой на конце
На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F cdot l$.
Уравнения изгибающих моментов
$M(x) = — Fl + Fx = F(x — l)$
Уравнение углов поворота
$EI,y'(x) = EI,varphi (x) = int dx + C = F(frac<<>> — lx) + C$
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$left < beginEI,varphi (0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$
Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = frac<<F,>><>$.
Максимальный угол поворота сечения также будет иметь место при $x = l$
знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.
Видео:Построение эпюр в консольной балкеСкачать

Шарнирно закрепленная балка с силой посередине
На опорах возникают вертикальные реакции $ = = F/2$.
Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид
$M(x) = fracx$, то есть $EI,y»(x) = fracx$, интегрируем дважды
Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l/2$
Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).
Видео:Понимание напряжений в балкахСкачать

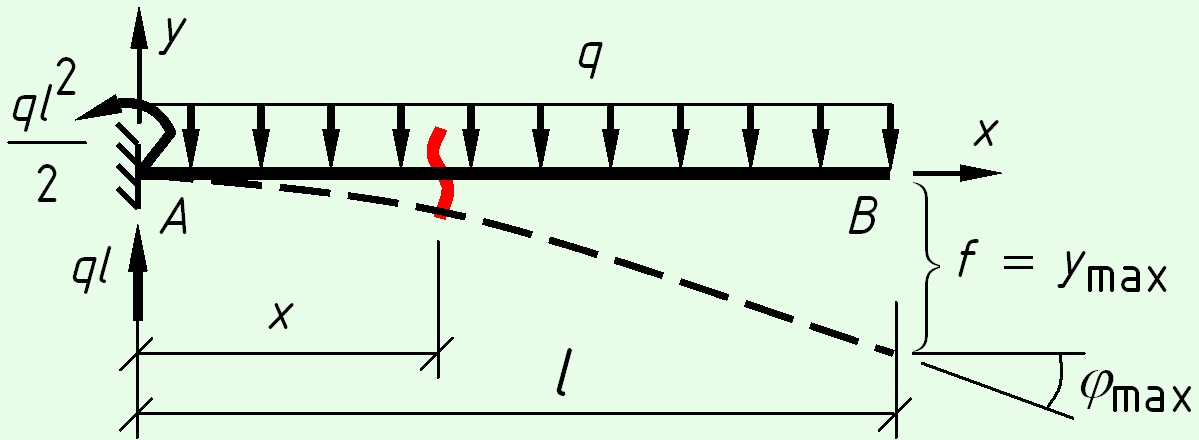
Консольная балка с равномерно распределенной нагрузкой
На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = frac<<q>>$.
$M(x) = — frac<<q>> + ql cdot x — frac<<q>>$, дважды интегрируем
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$left < beginEI,y'(0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$
Решение системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
Максимальный угол поворота сечения также будет иметь место при $x = l$
🔍 Видео
Прогиб консоли (2). Уравнение осиСкачать

Изгиб Л.4 \ ДУ изогнутой оси (метод Коши-Крылова)Скачать

Определение реакций опор в жесткой заделке консольной балкиСкачать

Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать

Определение реакций опор в балке. Сопромат.Скачать

Построение эпюр при изгибе. Часть 1. Консольная балкаСкачать
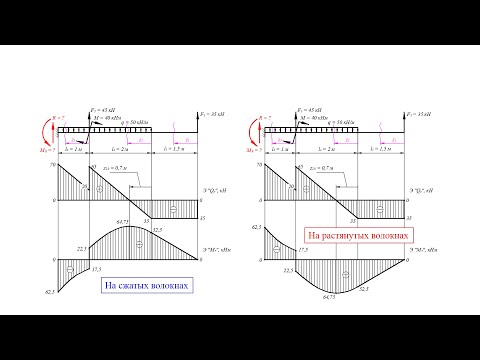
БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Определение опорных реакций в заделке консольной балкиСкачать

Построение эпюр в консольной балке ▶️ Расчет консольной балки на изгибСкачать

Метод начальных параметров ( МНП ). СопроматСкачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Определение опорных реакций в заделке ( балка ). СопроматСкачать

13. Метод начальных параметров ( практический курс по сопромату )Скачать

Расчет консольной балки на изгибСкачать

Изгиб балкиСкачать