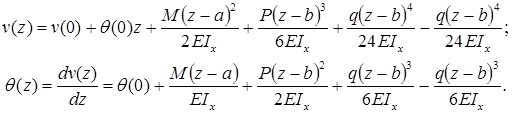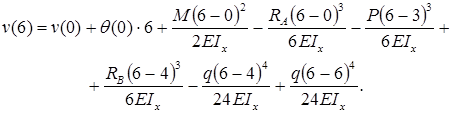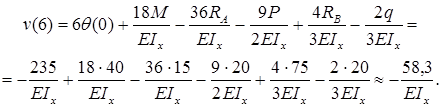Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

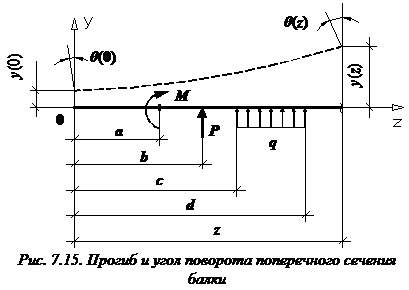
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 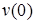и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Содержание

Уравнение упругой линии балки на примере
Дифференциальное уравнение упругой линии балки и его интегрирование
Перемещения в балках при изгибе
Виды перемещений при изгибе
Цель определения перемещений
Дифференциальное уравнение упругой линии (изогнутой оси) балки
📽️ Видео

Видео:Построение эпюры прогибов балкиСкачать

Уравнение упругой линии балки на примере

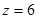
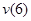
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .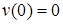

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

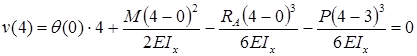
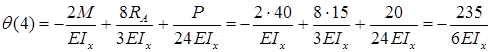
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

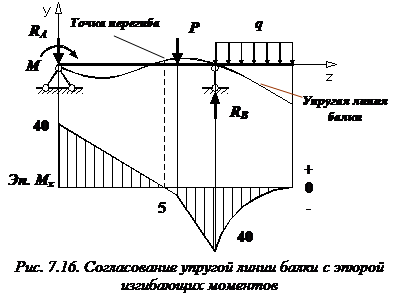
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

а после второго интегрирования – прогибы балки

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

Перемещения в балках при изгибе

Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Виды перемещений при изгибе

Упругая линия балки – ось балки после деформации.

Прогиб балки $y$ – поступательное перемещение центра тяжести в поперечном направлении балки. Прогиб вверх считаем положительным, вниз – ’ емким.

Уравнение упругой линии – математическая запись зависимости $y(x)$ (прогиба по длине балки).

Стрела прогиба $f = <y_>$ – максимальное по длине значение прогиба балки.

Угол поворота сечения $varphi $ – угол, на который поворачивается сечение в процессе деформирования балки. Угол поворота считаем положительным, если сечение поворачивается против часовой стрелки, и наоборот.

Угол поворота сечения равен углу наклона упругой линии. Таким образом, функция изменения угла поворота по длине балки равна первой производной от функции прогибов $varphi (x) = y'(x)$.

Таким образом, при изгибе рассматриваем два вида перемещений – прогиб и угол поворота сечения.

Видео:Определение реакций опор в балке. Сопромат.Скачать

Цель определения перемещений

Перемещение в стержневых системах (в частности в балках) определяются для обеспечения условий жесткости (прогибы ограничиваются строительными нормами).

Кроме этого, определение перемещений необходимо для расчета прочности статически невыдающихся систем.

Видео:БАЛКА С СИЛОЙ ПОД УГЛОМ. Реакции опор. Техническая механикаСкачать

Дифференциальное уравнение упругой линии (изогнутой оси) балки

На данном этапе необходимо установить зависимость перемещений в балке от внешних нагрузок, способа закрепления, размеров балки и материала. Для полного решения задачи необходимо получить функцию прогибов $y(x)$ по всей длине балки. Вполне очевидно, что перемещения в балке зависят от деформаций каждого сечения. Ранее нами была получена зависимость кривизны сечения балки от изгибающего момента, действующего в этом сечении.

Кривизна линии определяется ее уравнением $y(x)$ так

где $y’$ и $y$ – соответственно, первая и вторая производная от функции прогибов с координатой x.

С практической точки зрения эту запись можно упростить. На самом деле $y’ = varphi $ – угол поворота сечения в реальных конструкциях не может быть большим, как правило не больше 1град = 0,017рад . Тогда $1 + <left( right)^2> = 1 + = 1.000289 approx 1$, то есть можно считать, что $frac = y» = frac<<y>><<d>>$. Таким образом, мы получили уравнение упругой линии балки (дифференциальное уравнение изогнутой оси балки). Это уравнение впервые получено Эйлером.

Получена дифференциальная зависимость показывает взаимосвязи между перемещениями и внутренними усилиями в балках. Учитывая дифференциальную зависимость между поперечной силой, изгибающим моментом и поперечной нагрузкой, покажем содержание производных от функции прогибов.

$y(x)$ – функция прогибов;

$y'(x) = varphi (x)$ – функция углов поворота;

$EI cdot y»(x) = M(x)$ – функция изменения изгибающего момента;

$EI cdot y»‘(x) = M'(x) = Q(x)$ – функция изменения поперечной силы;

$EI cdot <y^>(x) = M»(x) = q(x)$ – функция изменения поперечной нагрузки.