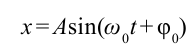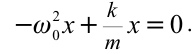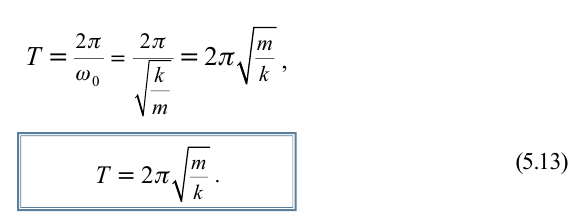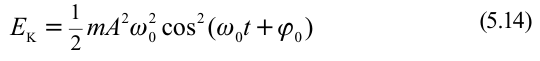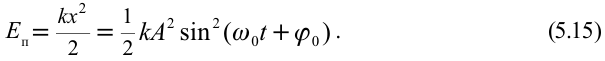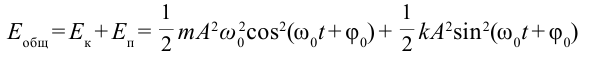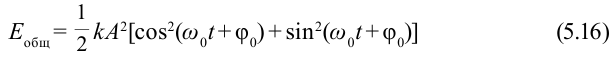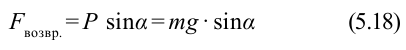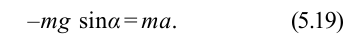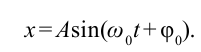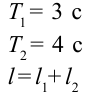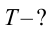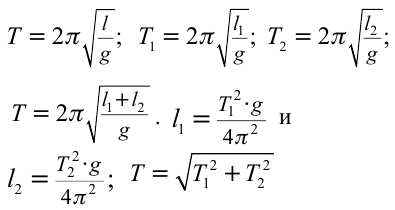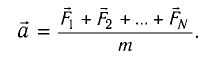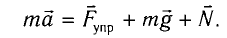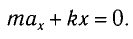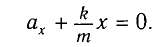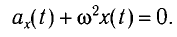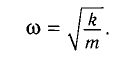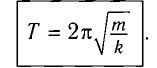- Определение и формулы математического маятника
- Уравнение движения математического маятника
- Циклическая частота и период колебаний математического маятника
- Уравнение энергии для математического маятника
- Примеры задач с решением
- Математический маятник: период, ускорение и формулы
- Общие сведения о механической системе
- Свойства маятника
- Период математического маятника
- Колебания математического маятника
- Колебательные движения маятника
- Математический маятник (формулы для больших амплитуд)
- Пружинные и математические маятники в физике — виды, формулы и определения с примерами
- Пружинный и математический маятники
- 🔍 Видео
Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Определение и формулы математического маятника
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.
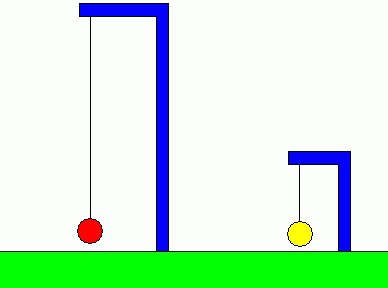
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Видео:Математический маятник или откуда формула периодаСкачать

Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
где $alpha $ — начальная фаза колебаний; $_0$ — амплитуда колебаний; $_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Видео:Колебания математического маятникаСкачать

Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
Период колебаний математического маятника ($T$) в этом случае равен:
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
Максимальное значение потенциальной энергии математического маятника равно:
Максимальная величина кинетической энергии:
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=_0x_m$ — максимальная скорость.
Видео:Почти всё о маятникеСкачать

Примеры задач с решением
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
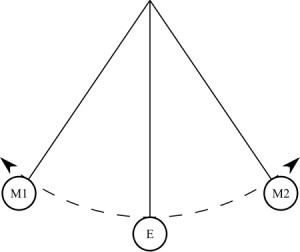
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
Из уравнения (1.1) найдем искомую высоту:
Ответ. $h=frac$
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
Выразим из нее ускорение:
Проведем вычисления ускорения силы тяжести:
Ответ. $g=9,87 frac$
Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Математический маятник: период, ускорение и формулы
Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень. Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.
Видео:Период математического маятника. В школе обманывали?Скачать

Общие сведения о механической системе
Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос. В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название. Ее называют маятником Капицы.
Видео:Теормех. 2021-окт-18. Группа ПМФ. Двойной маятникСкачать

Свойства маятника
• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.
• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» — время, «изос» — равный).
Видео:Откуда берётся формула математического маятника?🤯🤯🤯Скачать

Период математического маятника
Этот показатель представляет собой период собственных колебаний. Несмотря на сложную формулировку, сам процесс очень прост. Если длина нити математического маятника L, а ускорение свободного падения g, то эта величина равна:
Период малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.
Видео:Урок 94 (осн). Задачи на колебательное движениеСкачать

Колебания математического маятника
Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:
где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так:
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Колебательные движения маятника
Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:
где θ0 – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.
Видео:Миноры и алгебраические дополненияСкачать

Математический маятник (формулы для больших амплитуд)
Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле:
sin x/2 = u * sn(ωt/u),
где sn — синус Якоби, который для u 2 августа, 2014
Видео:Математические и пружинные маятники. 11 класс.Скачать

Пружинные и математические маятники в физике — виды, формулы и определения с примерами
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
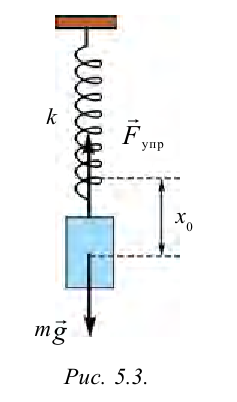
Система, состоящая из груза массой
Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
Если учесть, что ускорение тела, совершающего гармонические колебания 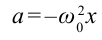
Из этого уравнения мы имеем:
Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника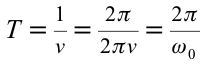
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 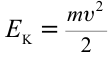
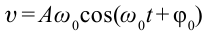
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
В большинстве случаев важно знать полную энергию системы:
Если учесть, что 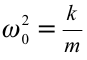
Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
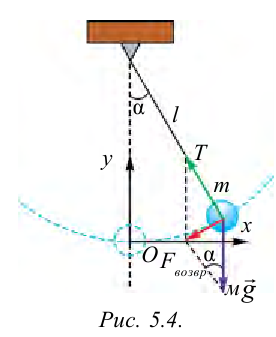
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 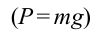

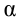
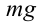

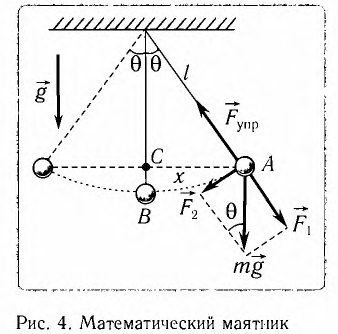
Из рис. 5.4. видим, что:
Согласно второму закону Ньютона, сила 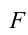
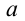
Из-за того, что угол наклона очень маленький 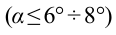
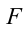
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 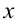
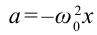
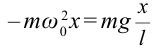
Следовательно 
Исходя из смысла периода колебания и учитывая, что 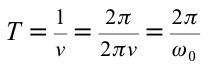
Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 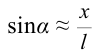
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Решение: 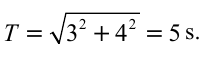
Ответ: 5 cек.
Видео:Теормех. 2021-окт-15. Группа РФЗ. Уравнения Лагранжа.Скачать

Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 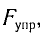
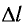
где k — жесткость тела, 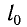
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
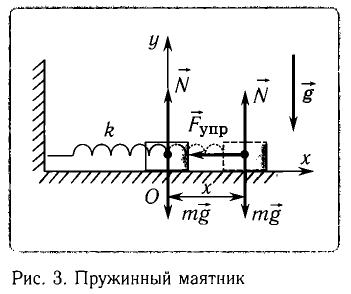
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 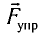
Запишем второй закон Ньютона для движения груза:
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
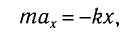
Это уравнение аналогично уравнению гармонических колебаний
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
Тогда период колебаний пружинного маятника можно найти по формуле
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 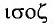
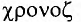
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Колебания математического маятникаСкачать

Период колебаний математического маятника 🧬 #shorts #умскул_физика #егэ2023 #егэфизикаСкачать

9. Колебания физического маятникаСкачать

ЧЕМ МОЖЕТ ОБЕРНУТЬСЯ ГАДАНИЕ НА МАЯТНИКЕСкачать

Урок 327. Гармонические колебанияСкачать

Негармонические колебания физического маятникаСкачать