С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.
Пусть в пространстве задана прямоугольная декартова система координат.
Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида
в котором хотя бы один из коэффициентов 
Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.
Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.
Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллипсоидом (рис. 2.22) .
1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что 
2. Эллипсоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно координатных осей,
· плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.
Примечание. Сфера является частным случаем эллипсоида при а= b =с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R 2 принимает вид 
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллиптическим параболоидом (рис. 2.23) .
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных осей 0xz и 0yz .
3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23).
Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.
Если полуоси равны a = b , то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0z , получается окружность.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется гиперболическим параболоидом (рис . 2.24).
Свойства гиперболического параболоида.
1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Гиперболический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных плоскостей 0xz и 0yz .
4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется однополостным гиперболоидом (рис. 2.25) .
Свойства однополостного гиперболоида.
1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25).
Если в уравнении (2.52) a = b , то сечения однополостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется двуполостным гиперболоидом (рис. 2.26) .
1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.
2. Двуполостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , при | z |> c получается эллипс, при | z |= c – точка, а в сечении плоскостями, перпендикулярными осям 0x и 0y , – гипербола (см. рис. 2.26).
Если в уравнении (2.53) a = b , то сечения двуполостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения.
Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х
С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.
Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.
Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости х0у. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости х0z или у0z.
Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:
1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение
2) круговые – нормальное сечение круг, при a = b = r уравнение
3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение
4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение
5) общего вида – нормальное сечение кривая случайного вида.
Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.
Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).
Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.
Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.
В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.
Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:

При а = b конус становится круговым.
Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии
Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядка. Цилиндрические поверхности.
Поверхность S называется цилиндрической поверхностью с образующей 
этой поверхности прямая, проходящая через эту точку параллельно образующей 
Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность 
уравнение f(x,y)=0, то S — цилиндрическая поверхность с образующей, параллельной оси OZ.
Кривая, задаваемая уравнением f(x,y)=0 в плоскости z=0, называется направляющей цилиндрической
поверхности.
Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность
называется цилиндрической поверхностью второго порядка.
Видео:Цилиндрические поверхностиСкачать
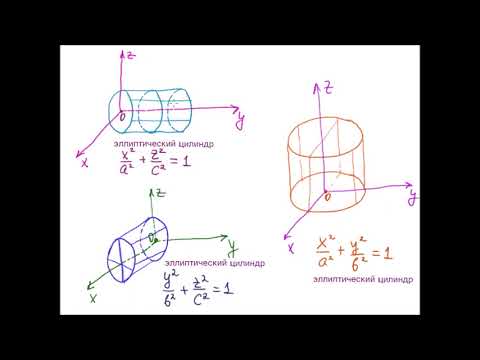
6.2. Цилиндрические поверхности
Или цилиндры. Под цилиндром также понимают геометрическое тело.
И это не совсем то, что обычно подразумевает обыватель – класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:
Задача 167
Построить поверхность, заданную уравнением
…что за дела?! Не опечатка ли здесь? Вроде как дано уравнение эллипса…
Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что использовали для плоскостей. Перепишем уравнение в виде 



Данная поверхность называется эллиптическим цилиндром. Эллипс 
Ось 
Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению 
Пространственное неравенство 

В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:
Задача 168
Построить поверхность, заданную уравнением
Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».
Сначала удобно построить окружность радиуса 

Полученные окружности (направляющие цилиндра) аккуратно соединяем 4 параллельными прямыми (образующими цилиндра):
Не забываем использовать пунктир для невидимых нам линий!
Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению 


Часто эту поверхность некорректно называют круговым цилиндром. Круглым! Круговой цилиндр, строго говоря – есть тело, по той причине, что его направляющей является круг. И тело, кстати, определяется неравенством 
Задача 169
Построить поверхность 
Перепишем уравнение в виде 




На этот раз я ограничился кусочком цилиндра на промежутке 
Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.
Теперь разбираемся с проекцией цилиндра на плоскость 
Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси 




Давайте заодно проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси 




А вот проекция на плоскость 


Задача 170
Построить поверхность 
Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат – выясните, какую именно часть цилиндра задаёт функция 
Цилиндрические поверхности могут быть смещены относительно координатных осей, например:



Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.
Параболические цилиндры
Как следует из названия, направляющей такого цилиндра является парабола.
Задача 171
Построить поверхность 
Не мог удержаться от этого примера =)
Решение: идём проторенной тропой. Перепишем уравнение в виде 





Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.
Теперь вторая часть задания, отыскание проекций:
1) Проекцией цилиндра на плоскость 

2) Проекция цилиндра на плоскость 

3) И, наконец, проекцией цилиндра на плоскость 

Задача 172
Построить параболические цилиндры:
а) 
б) 
В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину.
Я и сам особо не заморачиваюсь над красотой линий – если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉
Гиперболические цилиндры
Направляющими таких цилиндров являются гиперболы.
Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, и поэтому я ограничился единственным схематическим чертежом гиперболического цилиндра 
Принцип рассуждения здесь точно такой же – обычная «школьная» гипербола 

📹 Видео
Математика без Ху!ни. Уравнение плоскости.Скачать

Поверхности второго порядкаСкачать

553. Уравнение цилиндрической поверхности.Скачать

§63 Цилиндрические поверхностиСкачать

11 класс, 20 урок, Уравнение сферыСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости. 11 класс.Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Поверхности второго порядка. Поверхности вращенияСкачать
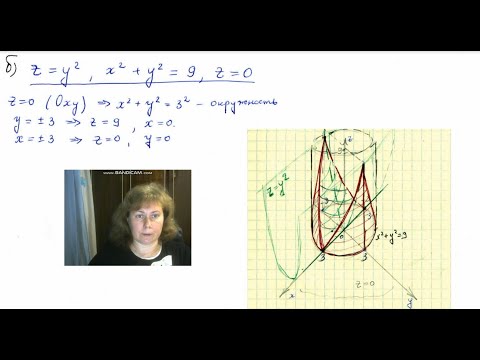
Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Объём цилиндраСкачать

Подготовка к зачету по аналитической геометрииСкачать

Уравнения кривых в пространствеСкачать

§55 Цилиндрическая система координатСкачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать

















