5. Параметрическое уравнение циклоиды и уравнение в декартовых координатах
Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.
Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:
х= OF = ON — NF = NM — MG = at-a sin t,
y= FM = NG = ND – GD = a – a cos t
Итак параметрические уравнения циклоиды имеют вид:
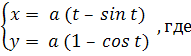
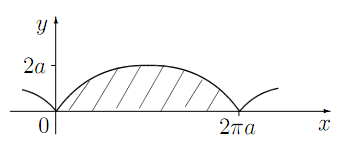
При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.
Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:
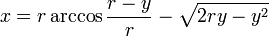
6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой
Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически
Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:
Площадь криволинейного сектора.
Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].
Будем считать, что r и ϕ — полярные координаты точки. Тогда любому
r0 — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную
уравнением r = r(ϕ).
Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных
координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.
Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь
криволинейного сектора вычисляется по формуле:
Эта теорема была доказана ранее в теме определенного интеграла.
Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.
Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,
Задача №2. Найти длину одной арки циклоиды
Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.
Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на [a, b], то AB является спрямляемой и
Следствие. Пусть AB задана параметрически
LAB = 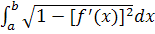
Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда
формулу (1) можно записать так
Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= 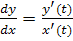
dx= x’(t)dt и, следовательно:
А теперь вернемся к решении нашей задачи.
Решение. Имеем 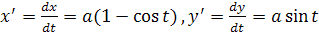
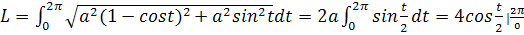
Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды
В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке [a,b] параметрически: x=φ(t), y=ψ(t) (t0 ≤t ≤t1)
|S|=
Применяя эту формулу для нашего уравнения циклоиды получаем:
Задача №4. Найти объем тела, полученного при вращении арки циклоиды
В интегральном исчислении при изучении объемов есть следующее замечание:
Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле
Воспользуемся этой формулой для нахождения нужного нам объема.
Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.
1. Берман Г.Н. Циклоида. – М., 1980
2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. — №5
3. Веров С.Г. Тайны циклоиды// Квант. – 1975. — №8.
4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.
5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. — №6.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969
[1] Такая линия и называется «огибающей». Всякая кривая линия есть огибающая своих касательных.
Видео:Кривые, заданные параметрическиСкачать

Уравнения кривых. Циклоида.
Циклоида (от греческого — круглый). – кривая которую формирует фиксированная точка окружности радиуса r, катящейся без скольжения по неподвижной прямой. Термин «циклоида» предложил Г. Галилей.
Точки, в которых циклоида пересекается с прямой, по которой катится окружность (эту окружность обозначают как производящую, а прямую, по которой она катится, – направляющую), обозначают как точки возврата, а самые высокие точки на циклоиде, размещенные посредине между соседними точками возврата, именуют вершинами циклоиды,
Обозначим горизонтальную ось координат как прямую, по которой катится формирующая окружность радиуса r. Тогда имеем нижеследующие уравнения в прямоугольной системе координат:
.
Циклоида характеризуется параметрическими уравнениями:
Циклоиду можно получить в результате решения дифференциального уравнения:
Видео:Кардиоида и нефроида, в общем - эпициклоида. Вывод параметрического уравнения.Скачать

Курсовая работа: Циклоида
| Название: Циклоида Раздел: Рефераты по математике Тип: курсовая работа Добавлен 01:30:14 21 января 2011 Похожие работы Просмотров: 2868 Комментариев: 22 Оценило: 6 человек Средний балл: 4.8 Оценка: 5 Скачать | ||
 |
3. Основные свойства касательной и нормали к циклоиде
Непосредственно очевидно, что ∟DOM равен 90° — φ.
Значит, ∟OMP = 90° — φ. Таким образом, получаем:
∟РМТ = ∟ОМТ — ∟ ОМР = 90° — 

Получается замечательный результат: угол РМТ оказывается равным углу РМЕ (см. теорему 2). Следовательно, прямые ME и МТ сольются! Наш рис. 18 сделан не совсем правильно! Правильное расположение линий дано на рис. 19.
Сформулируем полученный результат виде теоремы 3.
Теорема 3 (первое основное свойство циклоиды). Нормаль к циклоиде проходит через «нижнюю» точку производящего круга.
Из этой теоремы получается простое следствие. Угол между касательной и нормалью, по определению, — прямой. Это угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга. Итак, ТТ1 — диаметр, и T1 — «верхняя» точка производящего круга. Сформулируем полученный результат.
Следствие (второе основное свойство циклоиды). Касательная к циклоиде проходит через «верхнюю» точку производящего круга.
Что бы объяснить это свойство нам необходимо построить циклоиду.
Построение циклоиды производится в следующей последовательности:
1. На направляющей горизонтальной прямой откладывают отрезок АА12 , равный длине производящей окружности радиуса r, (2πr);
2. Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;
3. Окружность и отрезок АА12 делят на несколько равных частей, например на 12;
4. Из точек делений 1 1 , 2 1 , . 12 1 восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01 , 02 , . 012 ;
5. Из точек деления окружности 1, 2, . 12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;
6. Полученные точки А1 , А2 , . А12 принадлежат циклоиде.
На рис. 20 основание циклоиды разделено на 6 равных частей;
 |
чем число делений будет больше, тем, как мы знаем, чертеж получится точнее. В каждой точке циклоиды, построенной нами, проведем касательную, соединяя точку кривой с «верхней» точкой производящего круга. На нашем чертеже получилось семь касательных (из них две — вертикальные). Проводя теперь циклоиду от руки, будем заботиться, чтобы она действительно касалась каждой из этих касательных: это значительно увеличит точность чертежа. При этом сама циклоида будет огибать все эти касательные [1] ).
Проведем на том же рис. 20 нормали во всех найденных точках циклоиды. Всего будет, не считая направляющей, пять нормалей. Можно построить от руки сгибающую этих нормалей. Если бы мы вместо шести взяли 12 или 16 точек деления, то нормалей на чертеже было бы больше, и огибающая наметилась бы ясней. Такая огибающая всех нормалей играет важную роль при изучении свойств любой кривой линии. В случае циклоиды обнаруживается любопытный факт: огибающей нормалей циклоиды служит точно такая же циклоида, только сдвинутая на 2а вниз и на πа вправо. Этот факт характерен именно для циклоиды.
Теперь мы дадим определение циклоиды как геометрического места точек, не пользуясь механикой. Проще всего поступить так. Рассмотрим произвольную прямую АВ (будем условно считать ее направление горизонтальным) и на ней точку М0 . Далее рассмотрим всевозможные круги определенного радиуса, касающиеся этой прямой и расположенные по одну сторону от нее. На каждом круге от точки Т касания его с прямой АВ отложим (в направлении к точке М0 ) дугу ТМ, по длине равную отрезку М0 Т. Геометрическое место точек М (взятых на всех упомянутых нами кругах) и будет циклоидой.
Установим еще одно важное свойство циклоиды и попробуем именно его положить в основу изучения этой кривой.
Рассмотрим треугольник МТТ1 (рис. 21), образованный вертикальным диаметром производящего круга, касательной к циклоиде и нормалью к ней.
Связь между «высотой» и наклоном касательной
Угол МТ1 Т, как вписанный в окружность, равен половине центрального угла, опирающегося на ту же дугу, т. е. равен 
Обратим внимание на угол КМТ. Он равен углу МТ1 Т. Из треугольника ТМТ1 получаем:
МТ = 2а sin
а из треугольника ТКМ:
КТ = МТ sin-
Сопоставляя эти результаты и замечая, что КТ = h, получим окончательно:
h = 2asin 2
Мы выразили высоту точки М через угол между касательной в точке М и вертикалью (горизонталью мы по-прежнему считаем направление прямой АВ). Теперь выразим синус этого угла через «высоту». Получим, очевидно:
где черезk обозначена постоянная для данной циклоиды величина
Теорема 4. Синус угла между касательной к циклоиде в точке М и вертикалью пропорционален корню квадратному из «высоты» точки М.
Этим свойством обладает, очевидно, любая циклоида. Возникает вопрос: в какой мере это свойство характеризует именно циклоиду: будет ли всякая кривая, обладающая этим свойством, непременно циклоидой? Можно доказать, что это будет именно так, — что верна и следующая (обратная) теорема:
Теорема 5. Если даны прямая АВ и точка М, то единственной кривой, удовлетворяющей условиям теоремы 4 и проходящей через точку М, будет циклоида.
При этом радиус производящего круга этой циклоиды связан с коэффициентом k, о котором говорится в теореме 4, следующим соотношением:
 |
(Разумеется, расстояние точки М от АВ должно быть меньше, чем 2а.)
Строгое доказательство этой теоремы средствами элементарной математики очень громоздко, и мы его приводить здесь не будем.
Если в условии теоремы 5 не оговорить, что искомая кривая проходит через наперед указанную точку М, то получится не одна, а бесконечное множество циклоид, которые получаются друг из друга параллельным сдвигом по направлению прямой АВ (одна из них проходит через точку М, другая — через М1 третья — через М2 и т. д.). Это множество, или, как его называют, семейство циклоид изображено на рис. 22.
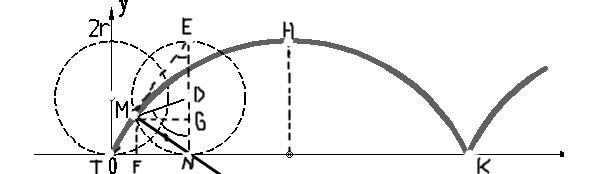
Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.
Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:
х= OF = ON — NF = NM — MG = at-a sin t,
y= FM = NG = ND – GD = a – a cos t
Итак параметрические уравнения циклоиды имеют вид:

Видео:§4 ЦиклоидаСкачать
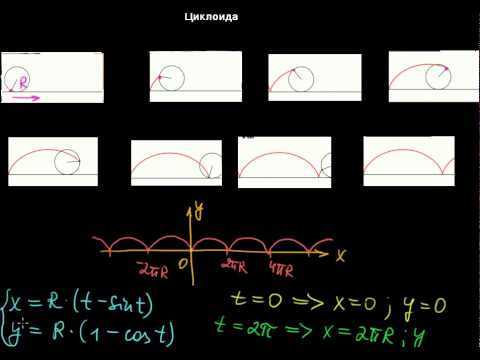
При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.
Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:

6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой
Задача №1 . Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически
Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:
Площадь криволинейного сектора.
Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].
Будем считать, что r и ϕ — полярные координаты точки. Тогда любому
r0 — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную
уравнением r = r(ϕ).
Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных
координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.
Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь
криволинейного сектора вычисляется по формуле:
Эта теорема была доказана ранее в теме определенного интеграла.
Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sint) , y= a (1 – cost) , и осью Ох, сводится к следующему решению.
Решение . Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,
Задача №2. Найти длину одной арки циклоиды
Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.
Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на [a, b], то AB является спрямляемой и
Следствие. Пусть AB задана параметрически
LAB = 
Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда
формулу (1) можно записать так
Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= 
dx= x’(t)dt и, следовательно:
А теперь вернемся к решении нашей задачи.
Решение . Имеем 

Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды
В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке [a,b] параметрически: x=φ(t), y=ψ(t) (t0 ≤t ≤t1 )
|S|=
Применяя эту формулу для нашего уравнения циклоиды получаем:
Задача №4. Найти объем тела, полученного при вращении арки циклоиды
В интегральном исчислении при изучении объемов есть следующее замечание:
Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле
Воспользуемся этой формулой для нахождения нужного нам объема.
Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.
1. Берман Г.Н. Циклоида. – М., 1980
2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. — №5
3. Веров С.Г. Тайны циклоиды// Квант. – 1975. — №8.
4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.
5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. — №6.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969
[1] Такая линия и называется «огибающей». Всякая кривая линия есть огибающая своих касательных.
💥 Видео
4K Что такое циклоида, cycloid curve constructionСкачать

14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

Площадь циклоиды.ЦиклоидаСкачать

построение циклоидыСкачать

Циклоида и сложение движенийСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Parametric curve: cycloid (Python, VGL, MoviePY)Скачать

Длина циклоидыСкачать

1695. Длина одной арки циклоиды.Скачать

Площадь под аркой циклоиды без интеграла и байки про ДекартаСкачать

Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Équations paramétriques, cycloïde, cardioïde et astroïdeСкачать

Как построить кривую, заданную параметрическиСкачать

Параметрические уравнения (часть 1)Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математика | Параметр. Система уравнений с параметромСкачать

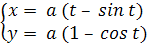
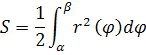
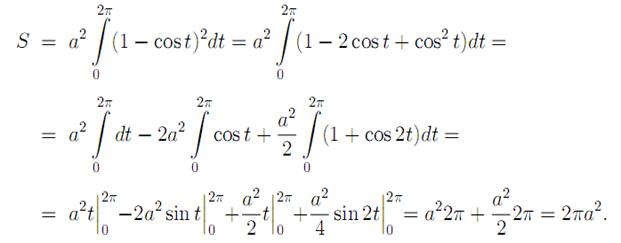
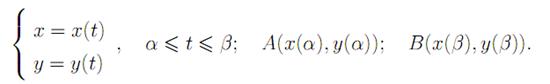
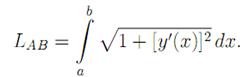
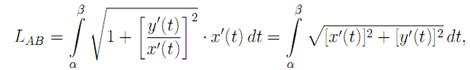
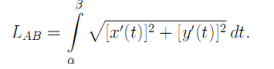
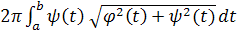
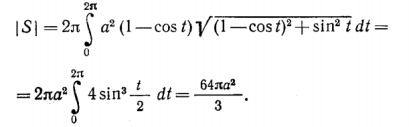
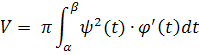
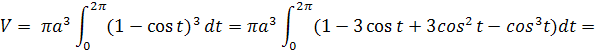
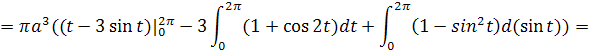
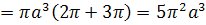



 Изучив движения по наклонным плоскостям, Галилей перешел к рассмотрению движения материальной точки под действием силы тяжести по ломаным линиям. Сравнивая времена движения по различным ломаным, соединяющим фиксированную пару точек А и В , Галилей заметил, что если через эти две точки А, В провести четверть окружности и вписать в нее две ломаные М иL , такие, что ломанаяL «вписана» в ломаную М, то материальная точка из А в В быстрее попадает по ломаной М, чем по ломаной L. Увеличивая у ломаной число звеньев и переходя к пределу, Галилей получил, что по четверти окружности, соединяющей две заданные точки, материальная точка спустится быстрее, чем по любой вписанной в эту четверть окружности ломаной. Из этого Галилей сделал ничем не аргументированный вывод, что четверть окружности, соединяющая пару заданных точек А, В (не лежащих на одной вертикали), и будет для материальной точки, движущейся под действием силы тяжести, линией наискорейшего спуска (позже линию наискорейшего спуска стали называть брахистохроной). Впоследствии выяснилось, что это утверждение Галилея было не только необоснованным, но и ошибочным.
Изучив движения по наклонным плоскостям, Галилей перешел к рассмотрению движения материальной точки под действием силы тяжести по ломаным линиям. Сравнивая времена движения по различным ломаным, соединяющим фиксированную пару точек А и В , Галилей заметил, что если через эти две точки А, В провести четверть окружности и вписать в нее две ломаные М иL , такие, что ломанаяL «вписана» в ломаную М, то материальная точка из А в В быстрее попадает по ломаной М, чем по ломаной L. Увеличивая у ломаной число звеньев и переходя к пределу, Галилей получил, что по четверти окружности, соединяющей две заданные точки, материальная точка спустится быстрее, чем по любой вписанной в эту четверть окружности ломаной. Из этого Галилей сделал ничем не аргументированный вывод, что четверть окружности, соединяющая пару заданных точек А, В (не лежащих на одной вертикали), и будет для материальной точки, движущейся под действием силы тяжести, линией наискорейшего спуска (позже линию наискорейшего спуска стали называть брахистохроной). Впоследствии выяснилось, что это утверждение Галилея было не только необоснованным, но и ошибочным.

 или
или .
. поворота радиуса производящего круга называть «основным углом». Значит, угол МОТ на рис. 17 — основной угол. Будем считать основной угол острым. Читатель сам видоизменит рассуждения для случая тупого угла, т. е. для случая, когда катящийся круг сделает больше четверти полного оборота.
поворота радиуса производящего круга называть «основным углом». Значит, угол МОТ на рис. 17 — основной угол. Будем считать основной угол острым. Читатель сам видоизменит рассуждения для случая тупого угла, т. е. для случая, когда катящийся круг сделает больше четверти полного оборота. что и требовалось доказать.
что и требовалось доказать.
 , а каждый из углов при основании — половике этой суммы. Итак,
, а каждый из углов при основании — половике этой суммы. Итак,

















