Уравнение тренда описывает тенденцию развития изучаемого показателя в зависимости от времени декан (2 видео)

Анализ тенденций развития показателей

Теоретические аспекты анализа тенденций развития

Показателей

Анализ тенденции развития показателя является вариантом горизонтального анализа, при котором определение изменений производится за несколько последовательных периодов.

Для отображения процесса развития экономических явлений во времени строят ряды динамики. Важным направлением в исследовании закономерностей динамики экономических процессов предприятия является изучение общей тенденции развития. Тенденция – направление, в котором совершается развитие какого-либо явления. Анализ тенденции развития позволяет выявить основное направление, в котором совершается развитие показателя во времени: рост, снижение, устойчивость, колебание.

В рыночной экономике анализ экономических показателей обязательно требует не только выявления, но и измерения закономерностей их развития во времени.

Потребность квалифицированного управления развитием коммерческой деятельности обуславливает необходимость придания основной тенденции развития обобщающей количественной оценки. Это можно осуществить, применяя специальные приемы анализа рядов динамики. Конкретное их использование предопределяется задачами анализа.

Более точно основную тенденцию развития показателя можно описать с помощью тренда. Под трендом понимают расчетную спрямляемую кривую изменения экономического показателя, параметры которого определяют путем математической обработки данных ряда динамики.

При наличии ряда наблюдаемых значений для различных моментов времени следует найти подходящую трендовую кривую, которая сгладила бы все остальные колебания. Прежде чем вычислить параметры уравнения тренда, необходимо выявить тип тенденции. Свойства развития отражает тип уравнения тренда, который может иметь прямолинейную, параболическую, гиперболическую и т.д. форму. Установление типа тренда выполняется разными способами. В современных ЭВМ алгоритмы определения параметров различных математических функций составляют содержание стандартных программ машинной обработки рядов динамики при анализе тренда.

На основе анализа тенденций можно делать выводы о ходе экономических процессов в будущем, поскольку полученные количественные оценки основной тенденции развитияпозволяют прогнозировать значения финансовых показателей.

Выявление и измерение закономерностей развития

Показателя во времени

Анализ тенденции развития выполните по одному из показателей, который был использован для расчета финансового коэффициента первого класса.

На первом этапе проведите анализ тенденции развития показателя с использованием статистических характеристик.

Для этого в табличном виде представьте изучаемый ряд динамики и его некоторые статистические характеристики:

1. Абсолютные изменения и темпы динамики показателя по сравнению с предыдущим годом

2. Среднегодовое абсолютное изменение и среднегодовой темп динамики за период;

При заполнении таблицы 10 в названии конкретизируйте наименование изучаемого показателя.

Таблица 10- Сведения о динамике показателя

Год	Значение показателя, млн руб.	Изменение (+, -) по сравнению с предыдущим годом, млн руб.	Цепной темп динамики, %
х	х

Для придания основной тенденции развития обобщающей количественной оценки рассчитайте среднегодовой абсолютный прирост и среднегодовой темп динамики показателя. Не забывайте везде писать название анализируемого показателя.

По исходным данным среднегодовое абсолютное изменение показателя за пять лет определите по формуле:

где значение исследуемого показателя на конец первого года;

значение исследуемого показателя на конец пятого года.

Обратите внимание на то, что среднегодовое абсолютное изменение показателя принято рассчитать с точностью, которая на один десятичный знак больше точности исходных данных.

По абсолютным уровням ряда динамики среднегодовой темп динамики показателя по данным предприятия за 5 лет определяется по формуле:

где значение исследуемого показателя на конец первого года;

значение исследуемого показателя на конец пятого года.

Среднегодовой темп динамики показателя рассчитайте с точностью до десятых долей процента.

На основе информации таблицы 10 и результатов дополнительно выполненных расчетов напишите выводы по анализу тенденции развития конкретного показателя за изучаемый период времени.

Во-первых, укажите общее направление изменения показателя за анализируемый период.

Во-вторых, уточните, в какие годы происходили наибольшие изменения.

В-третьих, раскройте экономический смысл абсолютного среднегодового изменения показателя, используя результат его расчета.

В-четвертых, охарактеризуйте, на сколько процентов в среднем ежегодно увеличивался (снижался) показатель за анализируемый период.

В-пятых, сравните абсолютное и относительное изменения показателя за последний год со среднегодовыми за период.

На втором этапе основную тенденцию развития показателя охарактеризуйте с помощью аналитического выражения тренда.

Математическую обработку данных ряда динамики желательно провести, используя знания, полученные при изучении дисциплины «Эконометрика».

В работе можно использовать «примитивный» вариант расчетов, условно считая, что динамика развития анализируемого показателя близка к прямолинейной. В этом случае тренд описывается уравнением прямой линии:

где свободный член уравнения,

коэффициент при переменной,

номер даты в ряду динамики (1,2,3 и т.д.).

Параметры тренда (уравнения регрессии) рассчитайте исходя из фактических значений показателя, используя метод наименьших квадратов.

Для прямолинейной зависимости параметры тренда можно установить, решив систему нормальных уравнений:

Для составления и решения данной системы уравнений предварительно следует подготовить информацию в таблице 11.

Таблица 11 — Информация для установления параметров тренда методом наименьших квадратов при прямолинейной зависимости

Номер года в ряду динамики ( )	Значение исследуемого показателя ( )
Сумма

Заполнив таблицу 11, используйте данные итоговой строки для составления системы уравнений.

Затем решите систему уравнений, т.е. найдите значения параметров «а» и «в» линейного уравнения с точностью до десятых (один знак после запятой). Обязательно приведите решение системы уравнений, поскольку Вы выполняете расчетно-графическую работу.

Определив значения параметров, запишите полученное уравнение регрессии, характеризующее изменение исследуемого показателя во времени.

Раскройте экономический смысл полученного числового коэффициента при переменной в полученном уравнении регрессии.

На рисунке 4 представьте фактическую динамику исследуемого показателя за анализируемый период и тренд.

Под рисунком напишите вывод о том, правильно ли отражают рассчитанные параметры уравнения регрессии (тренд) фактическую динамику показателя.

Полученные количественные оценки основной тенденции развития показателя, запишите в сводную таблицу 12.

Таблица 12 — Результаты анализа основной тенденции развития показателя

Показатель	Значение
Среднегодовой прирост, млн руб.
Среднегодовой темп динамики, %
Уравнение изменения показателя во времени (тренд)

При оформлении этой таблицы не забудьте указать точное название исследуемого показателя.

Содержание

Уравнение тренда описывает тенденцию развития изучаемого показателя в зависимости от времени декан
Тенденция во временном ряду
Линейный тренд
Параметры тренда
🎬 Видео

Видео:Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать

Уравнение тренда описывает тенденцию развития изучаемого показателя в зависимости от времени декан

Трендовая модель описывает изменение прогнозируемого или анализируемого показателя в зависимости только от времени, имеет вид у = f(t)- Неплохо описывает развитие (изменение) достаточно стабильной во времени социально-экономической системы, особенно таких агрегированных показателей развития, как ВНП (ВВП), МНП, НД, уровень инфляции, безработицы и т.п. [c.127]

Способ, использующий трендовые модели в прогнозировании, называется методом экстраполяции тренда. Это один из пассивных способов прогнозирования так называемый наивный про- [c.133]

Анализ движения процентных ставок и проверка их колебаний на случайность позволяют определить общую тенденцию развития показателя во времени с помощью построения трендовых моделей. Построение тренда состоит в аналитическом выравнивании эмпирических данных с целью сглаживания колебаний значений признака. Полученная таким образом общая тенденция развития явления трактуется как эволюционное изменение показателя во времени, свободное от воздействия случайных колебаний. [c.611]

Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов [c.612]

Для того чтобы получить максимально точный результат аналитического выравнивания эмпирических данных, характеризующих уровень процентных ставок, строят несколько трендовых моделей с применением различных аппроксимирующих функций. Далее, фактические и теоретические данные наносят на график и получают информацию о том, какая из выбранных функций наиболее реально отражает общую тенденцию развития исследуемого показателя. [c.613]

При моделировании уровней процентных ставок основной задачей является подбор типа функции, которая максимально точно описывает тенденцию развития изучаемого показателя. Механизм определения функции аналогичен выбору типа уравнения при построении трендовых моделей. На практике для решения этой задачи используют следующие правила. [c.619]

Q прогнозировать значение экономических показателей (построение трендовых моделей) [c.472]

Более надежный способ выявления основной тенденции развития рынка заключается в построении и графическом изображении трендовых моделей (так называемый метод статистического, или аналитического, выравнивания). [c.148]

К числу наиболее употребительных трендовых моделей относятся следующие [c.150]

Рис. 4.5. Трендовая модель тенденции развития рынка по прямой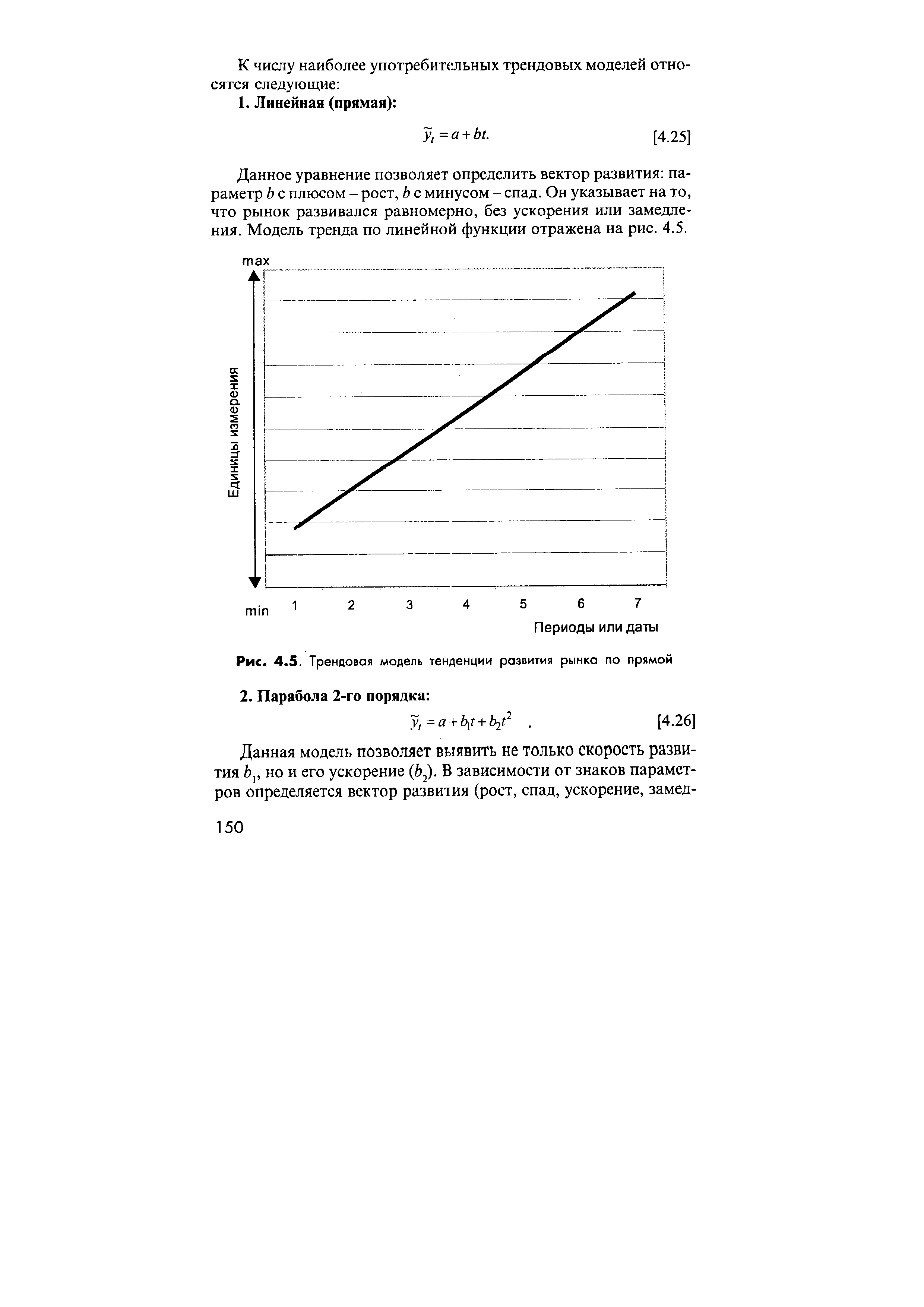

Уравнение тренда описывает тенденцию развития изучаемого показателя в зависимости от времени декан

Рис. 4.7. Трендовая модель тенденции развития рынка по экспоненте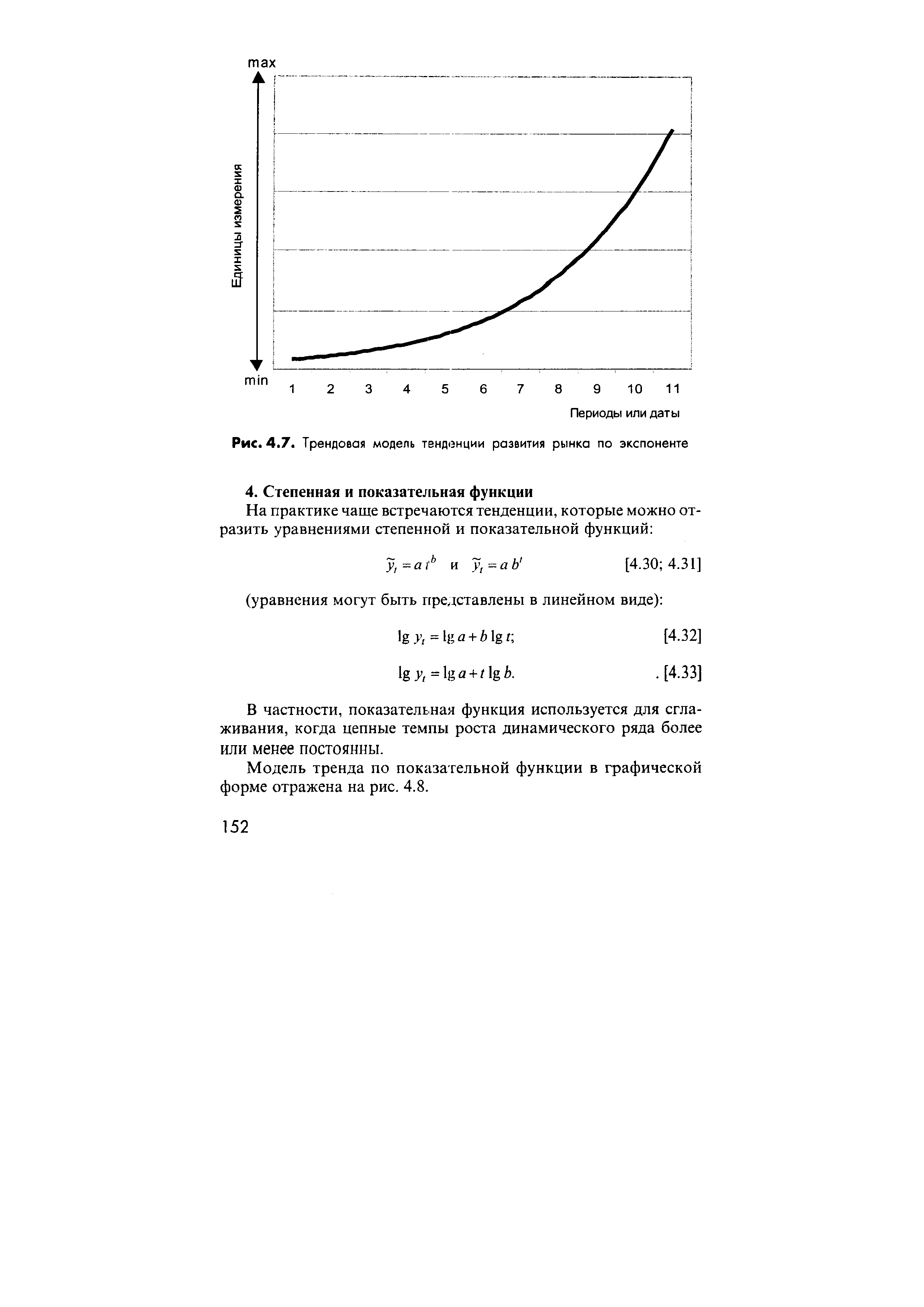

Рис. 4.9. Трендовая модель тенденции развития рынка по логарифмической функции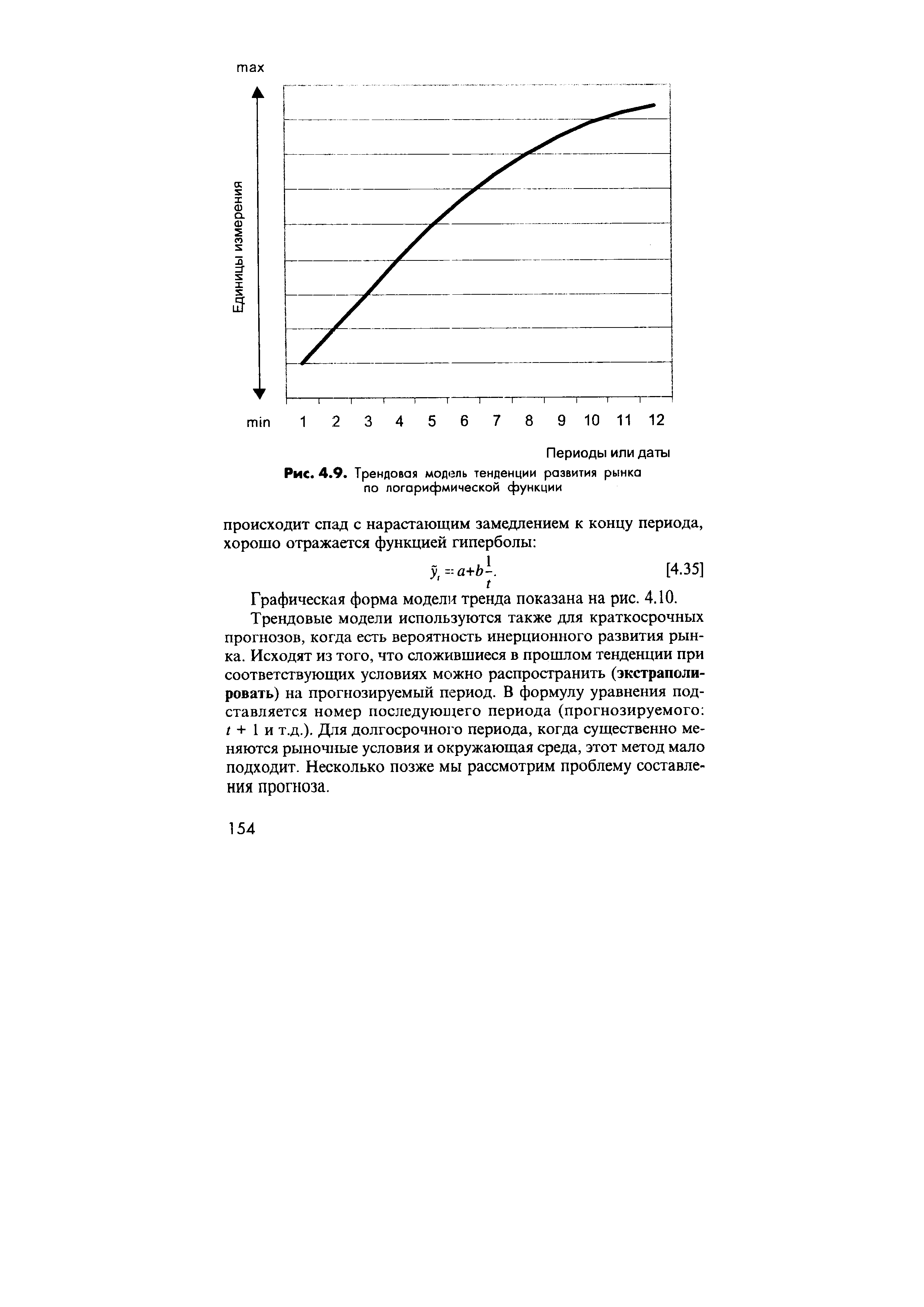

Трендовые модели используются также для краткосрочных прогнозов, когда есть вероятность инерционного развития рынка. Исходят из того, что сложившиеся в прошлом тенденции при соответствующих условиях можно распространить (экстраполировать) на прогнозируемый период. В формулу уравнения подставляется номер последующего периода (прогнозируемого t + 1 и т.д.). Для долгосрочного периода, когда существенно меняются рыночные условия и окружающая среда, этот метод мало подходит. Несколько позже мы рассмотрим проблему составления прогноза. [c.154]

Что собой представляет трендовая модель развития рынка [c.168]

Каковы различия экономической интерпретации прямолинейной и криволинейной трендовых моделей развития рынка [c.168]

Разработка стратегических трендовых моделей имеет ряд особенностей. Во-первых, должна быть обеспечена надежная долговременная информационная база расчета во-вторых, необходимо исключить внутригодовые сезонные и другие малые цикличные колебания, а также нерегулярные колебания в-третьих, допускается осуществление экстраполяции, которая при соблюдении определенных правил может рассматриваться как предварительный прогноз. [c.196]

Выбор функции для трендовой модели обусловлен характером динамического ряда, т.е. вектором развития спроса, скоростью его развития и колеблемостью эмпирических данных. В 3.2.4 приведены формулы основных функций, по которым строятся модели тренда. [c.196]

Прогнозирование рынка ценных бумаг с помощью трендовых моделей основано на разложении показателей, представленных вре- [c.263]

Трендовые модели. Правила построения и анализа. Подтверждения [c.39]

Если и линия сопротивления и линия поддержки сильные и достаточно долго удерживаются, то в зависимости от их сочетания возникают различные образы и ассоциации, которые и дают название трендовым моделям и фигурам. [c.40]

Общие черты и противоречия трендовых моделей [c.60]

Ниже мы рассмотрим на примерах все возможности, предоставляемые анализом средней. Важно при этом помнить, что данные правила будут хорошо работать только на правильно подобранных порядках средних Правильность выбора порядка средней проверяется на просмотре исторических данных — насколько информативной была данная средняя на предыдущем периоде времени, и обязательно практикой. Но если вы все сделали правильно, то результаты не замедлят себя показать. Метод анализа средних можно соотнести по значимости с анализом трендовых линий и моделей, если не больше. Вы будете получать выводы по направлению тренда, его силе и амплитуде, а также о ЖЦГ тренда. При этом метод анализа средних имеет очень важное преимущество перед анализом трендовых моделей, заключающееся в том, что средняя покажет вам раньше об изменениях, происходящих с трендом. Но старайтесь не строить свои решения на основе обычного анализа средних, когда тренд вялый или боковой. Запаздывание средних сведет на нет все ваши усилия по извлечению [c.67]

На рис. 22 представлен график зависимости курса GBP/USD 5 min от времени. На нем кривые скользящие средние тА(5) и тА(34) вычерчивают интересную фигуру, которую я назвал вентилятором. Ее особенность в том, что наблюдается определенная симметрия составных частей этой фигуры относительно точки пересечения (точка О на рис.22). Как известно из физики атомного ядра и элементарных частиц, законы симметрии (и подобия) универсальны в природе. Эти законы с успехом переносятся на различные трендовые модели в анализе рынка Форекс. Как видно из рис. 22, указанная выше симметрия позволяет сравнить ценовые проекции точек экстремума (максимальных отклонений быстрой скользящей тА(5) от медленной тА(34) величины АВ и А В ). Оказалось, что АВ приблизительно равна А В и чем горизонтальнее располагается медленная скользящая средняя (тА(34)), чем точнее выполняется это равенство. Исследования более 100 вентиляторов дало совпадение величин таких ценовых проекторов с точностью 38%. [c.45]

Еще раз напомню (и это очень важно), что доверять сигналам осцилляторов (из — за их вторичное относительно трендовых моделей) нужно только в направлении господствующей тенденции. [c.67]

Объем часто используют в качестве подтверждающего индикатора в анализе трендовых моделей (в частности, см. анализ поворотной модели голова — плечи в разделе 1.2.1). [c.70]

Теперь перейдем к поисковому прогнозу, который фактически решает задачу прогнозирования и отвечает на вопрос Что вероятнее всего произойдет при условии сохранения существующих тенденций . Для реализации поискового подхода часто используются различные статистические методы. В качестве примера рассмотрим схему прогнозирования по общей трендовой модели с использованием непротиворечивых экспертных оценок [9.18]. [c.350]

Прогноз спроса и предложения для газа строится на основе результатов расчетов макроэкономических показателей на предыдущем шаге (по годам), а не задается как внешний управляющий параметр. Это существенное отличие от имеющихся многочисленных упрощенных трендовых моделей прогнозов. [c.10]

Анализ тенденций развития рынка. Использование графиков (технического сглаживания) и трендовых моделей. Построение и интерпретация трендовых моделей. Цели и методы оценки устойчивости развития рынка. Оценки территориальной вариации параметров рынка. Характеристика сегментов рынка с позиции привлекательности для фирмы. Оценки соответствия правилу «тяжелой половины» Твельда или правилу «20 — 80» Парето. [c.150]

БШ — блоки статистических моделей. В таких блоках могут объединяться расчеты по моделям вида Б3.1 и Б3.2. Например, в блоке прогнозирования урожайности могут объединяться трендовые модели прогноза отдельных факторов изменения урожайности с много-факторной моделью прогнозирования урожайности. Примером более сложного блока статистических моделей являются эконометрические модели народнохозяйственного, регионального или отраслевого уровня, в которых при помощи экстраполяционных полиномов, корреляционных функций и регрессионных зависимостей устанавливается статистическая взаимосвязь между совокупностью характеризующих данный объект планирования экзогенных и эндогенных показателей. К таким моделям относятся, в частности, модели, разработанные в Украинском филиале НИИПиНа (УКР-1 и УКР-2), в НИИЭПе Госплана Литовской ССР и др. [c.136]

Используются и однофакторные модели, как например, модель. выражающая зависимости показателя экономегрического роста от времени (трендовая модель), или модель, выражающая зависимость показателя эконометрического роста только от величины трудовых ресурсов (L) для анализа и прогнозирования в краткосрочном периоде, когда изменение производственных фондов, т.е. капитала (К) незначительно по сравнению с предыдущим годом. [c.139]

Первым этапом построения тренда является выбор типа аналитической функции. В нашем примере основанием для применения линейного уравнения в качестве трендовой модели является существующая тенденция снижения уровня процентных ставок без наличия каких-либо осциллятивных колебаний. [c.612]

Для определенных видов диаграмм может быть вставлена линия тренда, с помощью которой выявляется тенденция изменения значений ряда. К линии тренда может быть выведено уравнение трендовой модели и рассчитан коэффициент аннрокеимации тренда, показаны прогнозные значения ряда. [c.476]

Наиболее широко в перечне методов маркетингового анализа представлена статистика. Методология маркетингового анализа использует следующие статистические методы абсолютные, средние, относительные величины, динамические ряды и ряды распределения, группировки, индексы, вариационный и дисперсионный анализ, корреляционно-регрессионный и многомерный анализ, графический метод, трендовые модели, методы экспертных оценок. Эконометрика в маркетинге представлена методами линейного и нелинейного моделирования, а также динамического программирования, моделями, базирующимися на теории массового обслуживания (теория очередей) и теории принятия решений (теория риска), имитационными моделями. Самостоятельное значение придается логистическим моделям управления г отоками товаров и денег и оптимизации товарных запасов. В маркетинговом анализе широко используются квалиметрические методы, а также методы социометрии. Стратегические матрицы (решетки), используемые в маркетинговом планировании для целей разработки оптимальной стратегии, могут найти применение и в маркетинговом анализе — для определения рейтинга фирмы и ее позиции на рынке, для прогноза риска и т.п. Немаловажное значение придается также неформальному описательному и качественному анализу, сценариям развития и т.п. [c.100]

Однако, как правило, динамика рынка изучается с помощью статистических методов обработки динамических рядов, позволяющих не только точно определить скорость и вектор развития, но и с помощью трендовых моделей выявить его основную тенденцию (тренд). Важную роль в анализе динамики рыночных процессов играет индексный метод, который обеспечивает возможность интегрированной оценки общего изменения сложных многоструктурных явлений (например, товарооборота) и позволяет выявить некоторые факторы развития (например, количественный и ценностный). Для анализа причинно-следственных связей в динамике целесообразно применять многофакторные статистические модели, которые могут быть использованы еще и для прогнозирования. В некоторых случаях используются методы многомерного анализа. Динамические процессы, структурные сдвиги, соотношения и т.п. легко проиллюстрировать методами графического анализа. [c.102]

Напомним, что линия тренда как бы осредняет колебания, равно удалена (в идеале) от точек, характеризующих эмпирические уровни динамического ряда. Это дает возможность использовать трендовую модель в целях измерения устойчивости раз- [c.158]

График 3. Обе линии BolHnger поднимаются вверх с незначительным расхождением. При такой динамике BolHnger курс может двигаться между средней (1.5050) и верхней линией ВВ (1.5750). По RSI трендовых моделей нет. Единственно можно предположить образование фигуры голова-плечи, но такая фигура подтвердится только при недостижении текущих значений RSI предыдущего максимума (81.5) и возврата к линии шеи (58.5). [c.116]

График З. Линии Bellinger незначительно расходятся в разных направлениях. Это сигнал усиления динамики курса. Но определенного бычьего тренда нет. При такой динамике линий курс может двигаться между средней (1.5150) и верхней линией ВВ (1.55). По RSI трендовых моделей нет. Только можно отметить параллельность динамики RSI и курса — в данной интерпретации это сигнал бычьего рынка. [c.118]

График 3. Линии Bellinger достаточно значительно расходятся. Курс вышел за верхнюю линию ВВ (1.5350). При такой динамике Bellinger курс может двигаться между средней (1.52) и верхней линией ВВ (1.54). По RSI трендовых моделей нет. [c.119]

Фурье анализе /51/. Если, к примеру, мы имеем некоторую слабо изменяющую функцию во времени (скажем курс валюты от времени во флэте), то для улавливания ее небольших изменений эту функцию пропускают через дифференциальный усилитель, а затем с помощью фазового детектора извлекают нужный сигнал. Другими словами, необходимо курс валюты во флэте продифференцировать, а затем с помощью подбора различных нормировочных коэффициентов фазового сдвига (во времени) придать полученной кривой индикативный вид. Именно в этом и заключается смысл осцилляторов это производная цены по времени, с каким — то временным сдвигом. Отсюда ясно, что осцилляторы на рынке Форекс по своей сути вторичны, т. е. любой их сигнал требует нескольких подтверждений, причем не других осцилляторов, а каких — то более — менее независимых от них индикаторов из трендовых моделей. [c.57]

ТРЕНДОВАЯ МОДЕЛЬ [trend model] — динамическая модель, в которой развитие моделируемой экономической системы отражается через тренд ее основных показателей (в частности, тренд средних величин этих показателей, их дисперсии, минимальных или максимальных уровней). [c.368]

Трендовая модель 368 Трение 368, 417 Треугольная матрица 368 Треугольная матрица МОБ 368 Трехиндексные задачи 123 Триангуляция матрицы МОБ 368 Труд 368 [c.492]

Видео:Аналитическое выравниваниеСкачать

Тенденция во временном ряду

Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.

Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.

Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.

К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Линейный тренд

Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.

Параметры тренда

Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.

Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.

Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.

По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста

При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.

Иллюстрация возможного появления ошибки спецификации приведем на рисунке

Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.