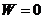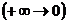12.1. Сохранение момента импульса в центральном поле.
Сила называется центральной, если для всех точек поля она направлена к одной и той же точке (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил, или силовым центром.
Уже из определения следует, что центральные силы консервативны.
Итак, центральная сила:
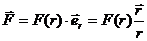
Поскольку эта сила консервативна, то можно ввести потенциальную энергию:
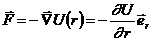
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:
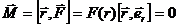
Тогда из уравнения моментов (11.5) получаем, что момент импульса есть постоянная величина.
При движении частицы в центральном поле полный момент импульса сохраняется, несмотря на то, что система (одна частица) не является замкнутой.

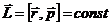
Так как 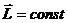
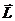
перпендикулярен к векторам 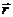
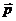
происходит в плоскости, перпендикулярной к 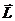
что частица в поле центральных сил движется по плоской орбите.
Если ось 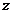
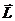
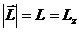
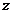
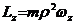
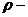
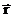
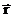
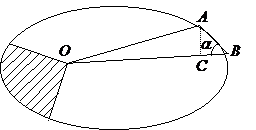 |
Пусть частица движется в в поле центральных сил по плоской траектории, представляющей собой замкнутую кривую.
Площадь 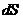
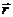
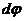
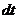
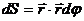
Выберем за начало отсчета точку О и найдем площадь сектора 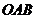
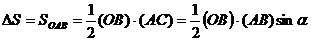
Здесь 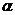
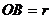
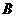
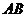
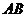
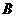
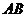
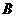
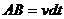
Тогда можем записать
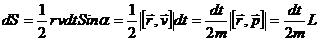
Вводя понятие секториальной скорости как площади, описываемой радиусом-вектором 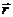
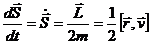
Т.о., мы получили математическое выражение 2-го закона Кеплера, устанавливающего постоянство секториальной скорости планеты 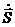
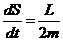
Этому закону подчиняется, например, движение планет по эллиптическим орбитам.
Примечание: Закон сохранения момента импульса частицы, движущейся в центральном поле иногда
называют “интегралом площадей”.
Итак, свойства движения частицы в центральном поле:
1) движение плоское, плоскость проходит через точку 0, определенный относительно которой момент импульса частицы сохраняется.
2) секториальная скорость постоянна (II закон Кеплера).
12.2. Закон сохранения энергии в центральном поле.
Центральные силы консервативны, следовательно, полная энергия частицы в системе «силовой центр – частица» (замкнутая система) сохраняется.
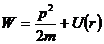
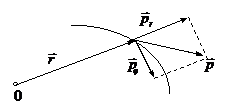
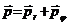
В полярных координатах выражения для момента импульса 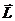
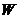
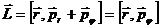
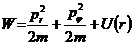
В выражении (12.10) 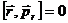
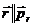
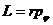
т.к. траектория частицы плоская и 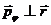
Если, воспользовавшись (12.10), исключить из уравнения (12.11) азимутальную составляющую импульса частицы 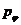
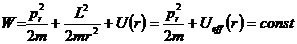
Примечание. Величину 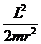
Уравнение (12.12) содержит только одну неизвестную – радиальную компоненту импульса 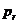
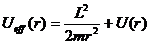
Т.о., можно сказать, что задача о движении частицы в центральном поле сводится к нахождению условий финитности (инфинитности) одномерного движения частицы в радиальном направлении в поле, описываемом эффективной потенциальной функцией 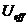
12.3. О траектории движения частицы.
Представим компоненты импульса, записанного в полярных координатах, следующим образом:
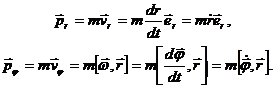
Далее, т.к. угол между вектором угловой скорости 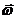
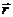
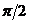
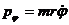
Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем
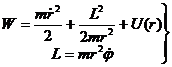
Из второго уравнения (12.15) получаем
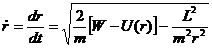
Разделяя переменные, находим в неявном виде зависимость 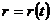
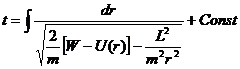
Из первого уравнения (12.15) имеем
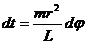
Исключив из уравнений (12.15) время 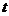
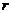
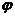
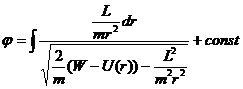
Значения 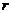
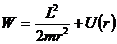
определяют границы области движения по расстоянию от центра поля. При выполнении равенства (12.18) радиальная скорость 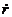
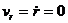
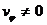
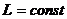
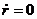
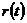
Если область допустимого изменения 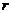
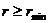
Если область изменения 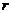
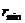
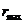
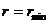
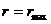
За время прохождения одной петли (от 
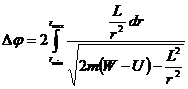
Условие замкнутости траектории: траектория будет замкнутой, если 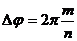
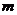
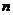
на угол, равный рациональной части от 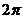
Тогда через 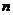
вектор точки, сделав 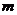
первоначальным значением, т.е. траектория замкнется.
Однако такой исход является скорее исключением,
нежели правилом. Существуют лишь два типа центральных
полей, в которых все траектории финитных движений
замкнуты. Это поля, где зависимость потенциальной энергии
от расстояния от центра поля имеет вид:
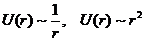
Задача Кеплера (Кеплерова задача) — задача о движении частицы в поле центральных сил, убывающих обратно пропорционально квадрату расстояния от центра поля. Этому закону подчиняются силы гравитационного притяжения между точечными массами (или телами, обладающими сферической симметрией), а также кулоновские силы, действующие между точечными электрическими зарядами. Поэтому такие поля являются важнейшим случаем центральных полей.
В таком поле потенциальная энергия частицы определяется выражением
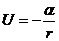
где 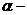
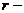
Рассмотрим случай, когда 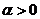

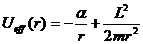
от расстояния от центра поля показана на рисунке.
При 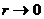
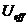
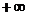
она стремится к нулю со стороны отрицательных
значений; при 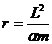
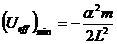
Из рисунка видно, что движение частицы будет инфинитным при 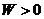
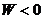
Форму траектории получаем интегрированием формулы (12.15) после подстановки 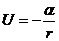
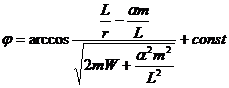
Выбирая начало отсчета угла 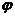
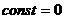
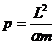
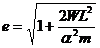
получим уравнение траектории в виде:
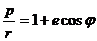
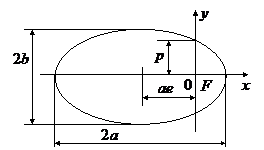
Приложение. Выражение (13.6) – уравнение конического сечения с фокусом в начале координат в полярных координатах; 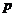
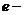
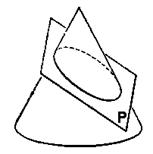
Коническими сечениями называют эллипс, параболу и гиперболу, т.к. их можно получить на поверхности
круглого конуса в пересечении с плоскостью 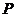
вершину конуса. При этом поверхность конуса предполагается
неограниченно продолженной в обе стороны от вершины.
Если плоскость 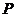
коническое сечение есть эллипс. Эллипсом называется геометрическое
место точек, сумма расстояний от которых до двух данных точек,
называемых его фокусами, есть величина постоянная. Отношение
фокусного расстояния эллипса к длине его большой оси называется
эксцентриситетом эллипса 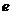
Если плоскость 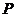
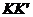
называют геометрическое место точек, равноотстоящих
от данной точки, называемой фокусом, и данной прямой
называемой директрисой. Исходя из её определения,
эксцентриситет параболы принимают равным единице
( 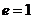
Если плоскость 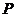
( 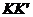
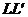
Гиперболой называется геометрическое место точек, разность
расстояний от которых до двух данных точек, называемых
фокусами, есть величина постоянная. Величина, определяемая
как отношение фокусного расстояния к длине действительной
оси (длина отрезка, соединяющего вершины гиперболы), называется
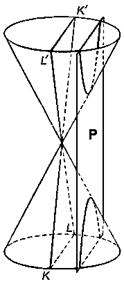
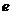
Из аналитической геометрии известно, что все эллипсы (кроме
окружности), параболы и гиперболы обладают следующим свойством: для
каждой из этих линий остается неизменным отношение
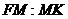
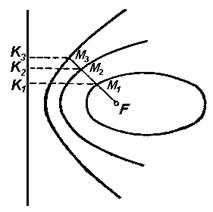
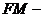
произвольной её точки 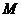
данной точки 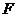
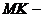
до данной прямой
Обобщая сказанное, можно дать
общее определение конического
сечения (эллипса, гиперболы и
параболы): коническое сечение есть
геометрическое место точек, отношение
расстояний которых до данной точки
(фокуса) и до данной прямой (директрисы) есть величина постоянная 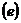
для эллипса 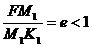
для параболы 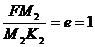
для гиперболы 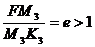
Из (13.5) следует, что при 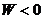
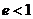
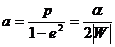
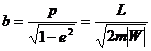
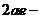
Из уравнения (13.6) следует, что точка с 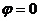
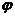
Наименьшее и наибольшее расстояния частицы от центра поля (фокуса эллипса) составляют (из 13.6)
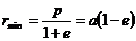
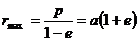
и зависят только от энергии частицы, поскольку из (13.7),
следует, что большая полуось эллипса 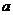
энергии, но не от момента импульса частицы).
Примечание. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце –
первый закон Кеплера.
Время обращения по эллиптической орбите (период 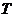
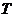
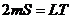
где 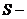
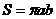
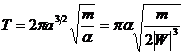
Тот факт, что квадрат периода обращения должен быть пропорционален кубу линейных размеров орбиты, составляет содержание третьего закона Кеплера.
Отметим, что период обращения, как следует из (13.11) зависит только от энергии частицы.
При 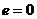
В случае если энергия частицы 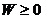
Если энергия частицы положительна 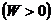
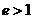
поля определяется выражением
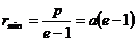
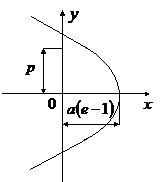
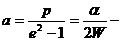
В случае, когда полная энергия частицы
эксцентриситет кривой 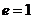
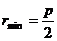
Этот случай реализуется, если частица начинает свое движение
из состояния покоя на бесконечности.
Используя выражение (13.9, 13.12 и 13.14) и соответствующие значения эксцентриситета, можно найти скорость частицы в перигелии при движении по всем рассмотренным траекториям. В точке поворота (перигелии) 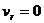
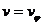
По окружности ( 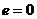
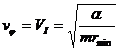
движению по параболе ( 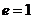
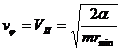
Если скорость частицы лежит в интервале
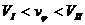
то её траекторией является эллипс ( 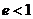
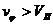
то траектория частицы имеет форму гиперболы ( 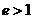
В небесной механике 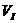
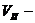
Обратимся теперь к движению в поле отталкивания, в котором потенциальная энергия частицы определяется выражением
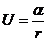
где 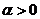
В этом случае эффективная потенциальная энергия частицы
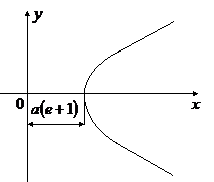
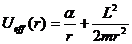
монотонно убывает от бесконечности до нуля
при изменении расстояния от центра поля от нуля до
бесконечности 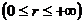
энергия частицы 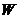
и её движение инфинитно. Все вычисления в этом случае
полностью аналогичны приведенным выше.
Траектория частицы является гиперболой
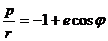
где характеристики кривой по-прежнему определяются
Двигаясь по такой траектории, частица проходит мимо центра поля, как показано на рисунке. Расстояние
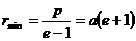
В заключение рассмотрения задачи Кеплера укажем, что при движении в поле центральных сил, котором потенциальная энергия частицы определяется выражением 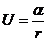
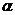
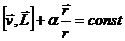
что легко проверить непосредственным вычислением, взяв от него производную по времени.
Сохраняющийся вектор (13.19) направлен вдоль большой оси от фокуса к перигелию и равен по величине 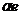
Интеграл движения, наряду с такими сохраняющимися величинами, полная энергия 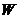
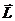
Видео:Кеплерова задача. Часть 1. Уравнение траекторииСкачать

Движение в центральном поле в физике







Видео:Траектория и уравнения движения точки. Задача 1Скачать

Движение в центральном поле в физике
- Перемещение центра поля Проблема движения двух объектов была сведена к проблеме движения одного объекта, что привело к проблеме определения движения частицы во внешнем поле, где существует потенциальная энергия.
Зависит только от определенного фиксированного расстояния r Точка; такое поле называется центральным. прочность F _ DU (G) _ DU R доктор др г Действуя на частицы, абсолютное значение Это также только от r и направлено на каждую точку вдоль радиус-вектора. При перемещении в центр, как уже указано в §9 Поле содержит момент системы относительно центра поля.
траектория частицы в центральном поле полностью находится в одной плоскости Людмила Фирмаль
Для одной частицы это М = [г]. Поскольку векторы M и r перпендикулярны друг другу, инвариантность m означает, что радиус-вектор всегда остается в одной плоскости (плоскости, перпендикулярной M) при движении частицы. Следовательно, .
Введите полярные координаты r и cp и запишите функцию Лагранжа в следующем формате (ср. (4.5)) L = ^ (r2 + r2cp2) -C / (r). (14.1) Эта функция явно не включает координаты cf. Обобщенные координаты, явно не включенные в Лагранжева функция называется патруль. Благодаря уравнению Лагранжа вы можете сделать следующее для этих координат: d d _ dL _ q dt dqi dqi ’ Таким образом, соответствующий обобщенный импульс p1 = db / dcc является интегралом движения.
- Эта ситуация значительно упрощает задачу интегрирования уравнений движения при наличии периодических координат. В этом случае обобщенный импульс = tg2f Соответствует моменту Mz = M (см. (9.6)), поэтому вернемся к известному закону сохранения момента M = gag2p = const. (14-2) Для плоского движения одной частицы в центре Районы, разрешенные этим законом Геометрическая интерпретация.
Формула (l / 2) r * rdcp представляет площадь сформированного сектора Два почти бесконечных радиуса вектора и элементы орбитальной дуги (рисунок 8). С этим? И мы пишем момент частицы на форме М = 2 т /, (14,3) Здесь производная / называется скоростью сектора.
сохранение импульса означает постоянство скорости сектора Людмила Фирмаль
по Напротив, — за тот же период радиус-вектор движущейся точки описывает равную площадь (так называемый Второй закон Кеплера) Полное решение проблемы движения центральной частицы Проще всего получить поле по закону сохранения энергии и импульса, не выписывая само уравнение движения.
Из (14.2), выражая φ через M и подставляя энергию в уравнение, E = (f2 + rV) + и (r) = ^ + J ^ + и (r). (14.4) Отсюда r = ± = J ^ [E-U (r) — ^ (14,5) дт в т т2г2 Или разделить и объединить переменные = [dr = + const. (14,6) J / 2, YYY 77, W м — [E-U (r)] Кроме того, напишите (14.2) в форме dip = -m ^ r2z dti Подставляя dt из (14.5) здесь, φ = [(М / г) др конст. (14-7) J y / 2t [E-U (g)] -M 2 / r2 V ‘ Уравнения (14.6) и (14.7) решают общую сформулированную задачу.
Второй из них определяет отношения между гифами. Орбитальное уравнение. Уравнение (14.6) неявно определяет расстояние r движущейся точки от центра как функцию Время. Обратите внимание, что угол φ всегда изменяется монотонно со временем — (14.2) показывает, что φ не меняет знак. Уравнение (14.4) показывает, что радиальная часть движется Его можно рассматривать как одномерное движение в поле с «эффективной» потенциальной энергией.
= Гг) + (14,8) Значение M2 / (2tr2) называется центробежной энергией. значение г Италбо йцинарг тюялеропо + & * = E ′ Перемещение расстояния от центра. Если выполнено уравнение (14.9), лучевая скорость r Она исчезнет. Это не означает остановку частиц Поскольку угловая скорость φ не исчезает, это истинное одномерное движение). Уравнение r = 0 означает «точку поворота» орбиты, где функция r (t) возрастает с ростом.
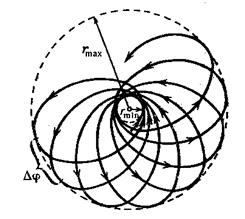
Уменьшить или наоборот. Если допустимая область изменения r ограничена только одним условием r ^ rmin, движение частицы бесконечно Траектория исходит из бесконечности и уходит к дьяволу Руки и ноги. Если есть две границы rmin и rmax в области флуктуаций r, Движение конечно и траектория полностью лежит В кольце, окруженном кружками r = rmax и r = = ^ min-
Однако это не означает, что траектория действительно является замкнутой кривой. р от При переходе от rmax к rmin, а затем к rmax радиус-вектор поворачивается на равный угол Df в соответствии с (14.7). Макс Der = 2 f, (M / r2) dr (14.10) J d / 2t (E-U) -M2 / g2 V 7 T минут Состояние закрытия орбиты Этот угол равен рациональному числу 2тг, т.е. была форма Df = 2 м / n, где w, n- Целое число Тогда н
Повторите этот период Завершить радиус-вектор момента времени, около t Компания соответствует ему Начальная стоимость То есть путь закрыт. Однако это исключение и для любой формы U (r) угол Не разумно Часть 2тг. Поэтому в общем случае орбита фи Движение пряжи не закрыто.
Она проходит минимальные и максимальные расстояния много раз Все кольцо между двумя граничными кругами заполняется за бесконечное время (например, как на рисунке 9). Есть только два типа в центральном поле. Все компактно поддерживаемые траектории замкнуты. Это поля, в которых потенциальная энергия частиц пропорциональна г Или г2.
Первый из этих случаев будет обсуждаться в следующем разделе, а второй случай соответствует так называемому пространственному осциллятору (см. Вопрос 3, §23). В точке поворота квадратный корень (14,5) (и И подынтегральные выражения (14.6) и (14.7) меняют знак.
Считая угол cp от направления вектора радиуса, нарисованного в точке поворота, отрезок траектории, примыкающий к этой точке с обеих сторон, отличается только знаком cp для всех одинаковых значений r.
Это означает, что траектория симметрична относительно указанного направления. введение Пройдите отрезок от одной из точек r = rmax локус к точке r = rmin, то есть симметрия Тот же сегмент до следующей точки Повторяя один и тот же отрезок в прямом и обратном направлениях, например, r = rmax, получается вся траектория.
Это Относится к двум бесконечным трекам Симметричная ветвь, отходящая от точки поворота Реклама бесконечна. Наличие центробежной энергии (при переходе от М ф 0), r- »0 до бесконечности, как smallfraclr2 Обычно перемещение делает вторжение невозможным Последние частицы в центре поля, даже если они сами обладают привлекательными свойствами.
«Падение» частиц в центр возможно только в том случае, если потенциальная энергия имеет тенденцию быть достаточно быстрой. k — для m — y0. Из неравенства V ^ — = E-U (r) -> 0 2 v ‘2mr2 или r2U (r) + Другими словами, U (r) должен стремиться -о либо-> ca> либо g2 2t Пропорционально —n> 2. Задание 1. Интегрировать уравнение движения шарикового маятника. Точка массы w движется вдоль поверхности сферы радиуса I Гравитационное поле.
Решения. Сферические координаты, начиная с центра сферы, Если полярная ось направлена вертикально вниз, функция Лагранжа Ник Координаты (р периодическая, поэтому обобщенный импульс сохраняется Rf, который соответствует мгновенному компоненту z: Интеграции (3) и (4) сводятся к эллиптическим интегралам соответственно. Но первый и третий вид.
Область движения вдоль угла 0 определяется условием E> Ј / eff и его гра. по ница-уравнению E = TJ3f. Последний куб Уравнение cos0 имеет два корня в интервале от -1 до +1, определенно Положение двух параллельных кругов на сфере, Вся траектория теперь закончилась. 2. Интегрировать уравнение движения массы Ожог вдоль поверхности конуса (угол 2а на вершине) Вертикально, сверху вниз, в гравитационном поле. Решения.
Функция Лагранжа L = t2 (02 + sin2 0 • ф2) + mgl cos 0. ml2 sin2 0 • ф = Mz = const. (I) Энергия-мгл cos0. (2) Определите 0 отсюда и отделите и получите переменную (3) Где вводится «эффективная потенциальная энергия» Интегралы (3) и (4) сводятся к эллиптическим интегралам типа 1 и типа 3 соответственно.
Область движения вдоль угла 0 определяется условием E> Ј / eff, а ее граница определяется уравнением E = TJ3ph. Последний куб Уравнение cos0. С двумя маршрутами, определяющими расположение двух параллельных окружностей на сфере, с интервалом от -1 до +1 Вся траектория теперь закончилась.
2. Интегрирует уравнение движения материальной точки, движущейся вдоль поверхности размещенного конуса (угол 2а у вершины) Вертикально, сверху вниз, в гравитационном поле. Решения. Функция Лагранжа Аналогично вопросу 1, PhD т = / ^ [E-eef (г)] Mz F Dr Фsin2 al / 2m: J / r2 JE-U3ф (r) ‘ + мср cos a- ML 2mr2 sin2 oc Условие E = ief (g) является кубическим уравнением для g (в случае Mz 0 0) и имеет два положительных корня.
Определите положение двух горизонтальных кругов на поверхности конуса. Траектория теперь закончена. 3. Объедините уравнение движения плоского маятника с точкой подвеса (с массой w ), которая может двигаться горизонтально (см. Рисунок 2). Решения. В функции Лагранжа в задаче 2 из § 5 координата x является периодической.
Следовательно, обобщенный импульс Px, который соответствует горизонтальной составляющей полного импульса системы, сохраняется. Px = (m i + GP2) x + 777-2 / f COS f = C Onst (1) Вы можете просмотреть всю систему в любое время. Тогда const = 0 и Интеграл уравнения (1) дает соотношение (T 1 + m2) х + m21 sinф = const, (2) Указывает, что центр инерции системы не перемещается горизонтально.
Используйте (1), чтобы получить энергию в следующем формате: ITI2I2 dcp. 11 (7771 + 7772) J VÅ + 7772 г / COSф 2 Координата X2 = x + lsin (p, 2/2 = lcos ((2) представляет p частицы m2, используя φ, траектория этой частицы — горизонтальная ось / 7771 / (7771 + m2) и вершина Вы можете видеть, что это эллиптический сегмент с I. I. 777-> oo, чтобы вернуться к нормальной математике Маятник, который рисует дугу круга.
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Ирина Пономарева — Орбитальная механика: уравнения движения в центральном полеСкачать

Реферат на тему «Движение в центральном симметричном поле»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

На тему «Движение в центральном симметричном поле»
Центральным называют такое силовое поле, в котором потенциальная энергия частицы является функцией только от расстояния r до определенной точки — центра поля: U = U ( r ). Сила, действующая на частицу в таком поле, тоже зависит лишь от расстояния r и направлена в каждой точке пространства вдоль радиуса, проведенного в эту точку из центра поля.
Хотя частица, движущаяся в таком поле, и не представляет собой замкнутую систему, тем не менее для нее выполняется закон сохранения момента импульса, если определять момент по отношению к центру поля. Действительно, поскольку направление действующей на частицу силы проходит через центр поля, то равно нулю плечо силы относительно этой точки, а потому равен нулю и момент силы. Согласно уравнению отсюда следует, что L = const .
(где L – вектор момента импульса, а K момент силы K = [ rF ]. Уравнение получается из уравнения L = [ rp ]. Определим производную по времени от момента импульса частицы. Согласно правилу дифференцирования произведения имеем
Так как — есть скорость v частицы, а p = m v , то первый член есть m [ vv ] и равен нулю, поскольку равно нулю векторное произведение любого вектора самого на себя. Во втором члене производная — есть, как мы знаем, действующая на частицу сила F . Таким образом, .)
Поскольку момент L = m [ rv ] перпендикулярен направлению радиуса-вектора r , то из постоянства направления L следует, что при движении частицы ее радиус-вектор должен оставаться все время в одной плоскости — плоскости, перпендикулярной направлению L. Таким образом, в центральном поле частицы движутся по плоским орбитам — орбитам, лежащим в плоскостях, проходящих через центр поля.
Данное уравнение можно записать в виде:
где ds — вектор перемещения материальной точки за время dt . Величина векторного произведешь двух векторов геометрически представляет собой лощадь построенного на них параллелограмма. Площадь же параллелограмма, построенного на векторах ds и r , есть удвоенная площадь бесконечно узкого сектора OAA ’ , описанного радиусом-вектором движущейся точки за время dt . Обозначив эту площадь через dS , можно записать величину момента в виде
Величина называется секториальной скоростью.
Задача о движении в центральном поле в особенности важна потому, что к ней сводится задача об относительном движении двух взаимодействующих друг с другом материальных точек — так называемая задача двух тел.
Если рассмотреть это движение в системе центра инерции обеих частиц. В этой системе отсчета суммарный импульс частиц равен нулю:
Из этих двух равенств получаются следующие формулы формулы
выражающие скорости каждой из частиц через их относительную скорость.
Подставив эти формулы в выражение полной энергии частиц получим
где U ( r ) — взаимная потенциальная энергия частиц как функция их относительного расстояния r . После простого приведения членов получим
где m обозначает величину
называемую приведенной массой частиц.
Мы видим, что энергия относительного движения двух частиц такая же, как если бы одна частица с массой m двигалась со скоростью в центральном внешнем поле с потенциальной энергией U ( r ). Другими словами, задача о движении двух частиц сводится к задаче о движении одной «приведенной» частицы во внешнем поле.
Видео:Курс «Баллистика и орбитальная механика» — «Уравнения движения тела в центральном поле»Скачать

Постановка задачи.
Видео:Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Движение в центральном полеСкачать

Рассмотрим энергию материальной точки в центральном поле сил.
, представим (скорость) в полярных координатах
📸 Видео
Лекция №8 "Движение точки в центральном поле"Скачать

Аналитическая механика 5. Движение точки в центральном поле.Скачать

Теоретическая механика. Лекция №5. Движение в центральном полеСкачать

Халилов В. Р. - Теоретическая механика - Движение в центрально-симметричном полеСкачать

Механика - Движение в поле центральных сил. Момент импульсаСкачать

Теормех. 2021-ноя-17. Движение в центральном полеСкачать

Кинематика точки Задание К1Скачать

ТЕОРМЕХСкачать

Теор.мех. 8. Движение в центральном полеСкачать

Лекция №5 "Момент импульса в квантовой механике. Движение в центральном поле"Скачать

Теормех. Центральное полеСкачать

Движение в центральных полях. Первые интегралы.Скачать

Степаньянц К. В. - Теоретическая механика I - Задача КеплераСкачать

Теормех. 2021-ноя-15. Группа ПМФСкачать