




Видео:Построение кривой в полярной системе координатСкачать

Скорость и ускорение точки в полярных координатах
- Рассмотрим движение точек на плоскости. В этом случае движение может быть задано в полярных координатах. Для этого возьмите точку O на плоскости в качестве полюса и нарисуйте от нее полярную ось, например, ось быка (рис. 22). Если радиус-вектор r и полярный угол = f2 (t) — (23). Полярный угол считается положительным, если он простирается от полярной оси против часовой стрелки до радиус-вектора. Радиус-вектор как расстояние от точки О до точки М принимает только положительные значения.
Уравнение (23) называется уравнением движения для полярных точек. Это также параметрические точечные траекторные уравнения. Исключение параметра-времени t из (23) дает орбитальное уравнение в полярных координатах. F (r, r = rr °, gr = gfr °. Для проекции скорости на ось, положительное направление которой совпадает с направлением единичного вектора r ° и jr с (24), vr = r, gr = gf. (26) Их называют лучевой и боковой скоростями соответственно. В зависимости от знака производной мицелия лучевая и боковая скорости являются как положительными, так и отрицательными. Используйте (24), чтобы определить ускорение точки в полярных координатах. У нас есть a = dv / dl = (d / d /) (rr 0 + gfr °).
Потенциальная энергия N материальной точки в мыслимой точке силового поля M осуществляется силой поля, действующей на материальную точку при перемещении из точки M в начальную точку Mo, т. Людмила Фирмаль
Проведите дифференциацию и получите a = rf ° + r + r fr 0 + r fr 0 + r f. Для производной по времени единичного вектора p ° dp0 / d ^ = φ (-r0), Вектор p ° вращается с той же угловой скоростью φ, что и вектор r °, поэтому единичным вектором, на который направлен вектор dp ° / dt, является вектор (-r °). Ускоряя производную единичного вектора и подставляя ее в уравнение, объединяющее члены, получаем в = (r-rf2) r ° + (rf + 2rf) p °. (27) Получены точечные ускорения разложения на радиальные ар и боковые ап компоненты. a = a, + ap, ar = (r-rf2) r °, ar = (rf + 2rf) p °. Для проекции ускорений на оси Or и Op получаем a, = r-rp2, ap = rp + 2rp. (28).
Ускорение ar называется радиальным, поперечным направлением. Боковое ускорение также может быть выражено в следующем формате: Эта формула для бокового ускорения широко используется при рассмотрении движения планет и искусственных спутников Земли. Рисунок 23 Равные производные по Поскольку радиальная и боковая составляющие ускорения перпендикулярны друг другу, Для фиксированных координатных осей Ox, Oy и Oz формула ax = dvx / dt, ay = dvy / dt, a2 = dv: / dt. Для подвижных осей Or и Op, как видно из (26) и (28), a и ap не являются временами от vr и vp. Особый случай.
- В этих уравнениях φ — угловая скорость вращения радиус-вектора, а φ — его угловое ускорение. Пример 1. Движение точки — это уравнение r = / (l + COSOH), φ = ШГ, Где я и со постоянные значения. Определить скорость и ускорение точки в полярных координатах траектории уравнения, времени t и момента Решения. Из уравнения движения уберите следующее уравнение для орбиты в полярных координатах: r = f (1 + C0 $ f). Это кардиоидное уравнение (рис. 24).
Проекции скорости и ускорения на полярную ось определяются уравнениями (26) и (28). У нас есть: Мы получаем «, = / = — / Eosin South. 1> = Гф = / ш (1 + COSO) /), t> = + = к ^ 2 (1 + 008 J = ^ 39» 6,2 м / с Прогноз ускорения всегда определяется по формуле а = -2 м / с2; ау = -6 м / с2; а =. > / ai + a * = s / 40×6,3 м / с2, ускорение геля n -2coszsinz + 36-2sin2 (i Ускорение при 2 ^ / 16 cos2 / + 36 sin2 2 / — ^ / 3 / 5® — 0,3 м / с. Далее для r = n / 6 с Скорость предопределена Боковая скорость при =, л / 6 с — по формуле х = 4sin / | Координаты движущейся точки при t = n / 6 на / 6 / 6м. y = 3cos2r | / 6 = 1,5 м. Отметьте положение движущейся точки на траектории в соответствии с координатами, выберите масштаб и нарисуйте векторы скорости и ускорения из проекции на ось.
Таким образом, принцип возможного смещения не является в действительности активной силой, и помимо сил реакции идеального соотношения, для которых задача не определена, определяются все силы энергосистемы. Людмила Фирмаль
Для радиальной составляющей скорости в рассматривается направление, противоположное единичному вектору r °. Это потому, что v был найден со знаком минус. Только числовое значение определяется для боковой составляющей скорости. Из рисунка 25 видно, что направление вектора противоположно направлению единичного вектора p ° (направление p ° получается поворотом вектора r ° на 90 ° против часовой стрелки). Следовательно, в рассматриваемом случае вы должны использовать знак минус для vp, то есть c, = -b, 2 м / с.
Для проверки правильности определения vp вы можете использовать следующую формулу «F. Нормальное ускорение всегда направлено внутрь вогнутой поверхности дорожки. Оказывается, что направление тангенциального ускорения а определяется а и направлено вдоль вектора скорости. В результате точка в определенной точке ускоряется. Определить радиус кривизны орбиты в момент времени t = 1/6 с. Все необходимые для этого количества уже доступны. получить = — = 39/5 «7,8
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координатах.
Если движение точки происходит в некоторой плоскости, то иногда целесообразно использовать полярную систему координат. Положение точки М в ней определяется координатами r и «фи», являющимися скалярными величинами.
Расположение полярной оси (луча, проведенного на плоскости из некоторой точки О) выбирают в плоскости движения точки, исходя из удобства решения задачи.
Полярный радиус r — скалярный неотрицательный параметр, равный длине отрезка ОМ, т.е. расстоянию от начала координат (точки О) до точки М.
Полярный угол «фи» — это угол между полярной осью и илнией ОМ (за положительное значение значение угла принимают направление, противоположное направлению движения часовой стрелки).
Для задания движения точки в полярной системе коодинат необходимо иметь уравнение движения в виде: 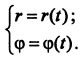
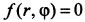
В полярной системе координат радиус-вектор точки, проведенный из центра О, равен 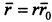
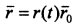
Вектор скоростипредставляется в виде суммы двух векторов, каждый из которых является составляющей скорости по направлению, задаваемому векторами r0 и p0 соответственно. Первое слагаемое называется радиальной составляющей, а второе — трансверсальной составляющей скорости точки: 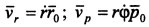
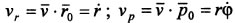
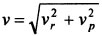
Ускорение точки: 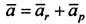
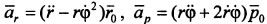
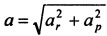
Дата добавления: 2018-11-26 ; просмотров: 1246 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔥 Видео
Полярная система координатСкачать

Видеоурок "Полярная система координат"Скачать

Скорость и ускорение точки в полярных координатахСкачать

Полярные координаты. Полярное уравнение эллипса.Скачать

Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Глаза гипножабы и площадь фигур в полярной системе координатСкачать

§30 Уравнения кривых второго порядка в полярных координатахСкачать

Полярная система координатСкачать

Оператор Лапласа в полярных координатахСкачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Площадь фигуры, заданной в полярной системе координатСкачать

§12 Полярное уравнение прямойСкачать

Построение графика функции в полярных координатахСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Двойной интеграл в полярных координатахСкачать

Овчинников А. В. - Аналитическая геометрия - Уравнения линий второго порядка в полярных координатахСкачать



