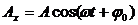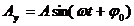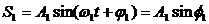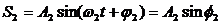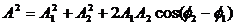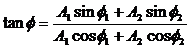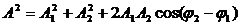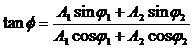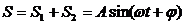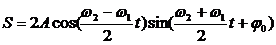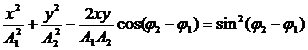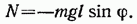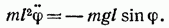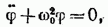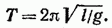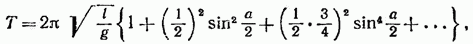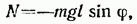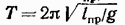Уравнение траектории точки участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты (3 видео)

Сложение гармонических колебаний

Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.

Содержание

Метод векторных диаграмм
Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты
Сложение взаимно перпендикулярных гармонических колебаний с кратными частотами
Дифференциальные уравнения колебаний
🔥 Видео

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Метод векторных диаграмм

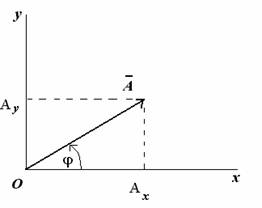
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j₀ где j₀ — начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

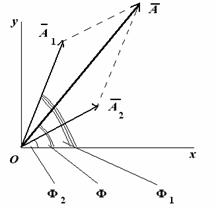
Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 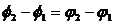, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

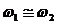
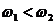
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

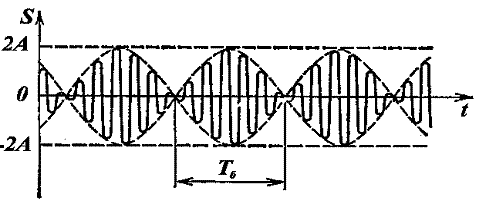
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 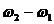— частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это — уравнение эллипса. При A₁=A₂ — окружность, при 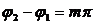(m — целое) — отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Видео:Сложение взаимно перпендикулярных гармонических колебанийСкачать

Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты

Два гармонических колебания с одинаковыми частотами происходят во взаимно перпендикулярных направлениях (по осям ОХ и OY):

В зависимости от соотношения амплитуд А,, А₂ и начальных фаз (pj, ф₂ складываемых колебаний точка будет двигаться или по эллипсу или по окружности или по прямым линиям (в 1,3 или 2,4 четвертях).

А) Пусть А, Ф А₂ и разность фаз Д(р = ф, — ф₂ = ±—, тогда

Возводим уравнения в квадрат и исключаем время:

Полученное уравнение или траектория движения точки является эллипсом с полуосями А, и А,. Если Aj = А₂, то эллипс превращается в окружность. Таким образом, результирующее движение точки — это движение с постоянной угловой скоростью со по эллипсу с полуосями А, и А2 (рис. 26,а) или по окружности с радиусом А = Aj = А₂ (рис. 26,6).

Рис. 26. Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты и с разностью фаз Л (р = ± 7Т 2: а — амплитуды колебаний различны: А2 >А у, б — амплитуды колебаний одинаковы: A i = А2 А

Б) Пусть Aj ф А₂ и разность фаз А А 2

ся в 1,3 четвертях координатной плоскости XOY (рис. 27).

Если Aj ф А₂ и разность фаз Аср = а₂ фа₁ : а — разность фаз А (р = 0; б- разность фаз Д 2 + А, .

Видео:Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать

Сложение взаимно перпендикулярных гармонических колебаний с кратными частотами

Пусть точка совершает одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях, но с различными частотами Oj ф од, • Если частоты или периоды Т_рТт этих колебаний относятся как целые числа:

(n, m — целые числа), то через промежуток времени, равный наименьшему общему кратному [1] обоих периодов, движущаяся точка снова возвращается в начальное положение. Определение уравнения траектории точки, участвующей в данных колебаниях в общем случае является трудной в математическом отношении задачей.

Траектория точки представляет сложную петлеобразную кривую. В общем случае вид траекторий зависит от соотношения между частотами, фазами и амплитудами колебаний.

Если периоды обоих колебаний совпадают неточно, то разность фаз все время меняется, вследствие чего траектория все время деформируется.

Если частоты обоих колебаний существенно отличаются друг от друга, то фигуры Лиссажу не наблюдаются.

Ниже на рис. 28 приведены фигуры Лиссажу для некоторых не очень сложных случаев, отличающихся разностью фаз и соотношением

Видео:Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Дифференциальные уравнения колебаний

— гармонические,

— затухающие,

— вынужденные.

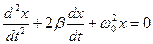
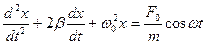
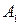
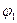
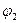
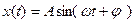
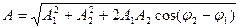
· Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых и , а начальные фазы и ,

, где

—

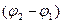
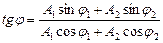
амплитуда результирующего колебания, — разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой

· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами

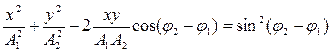
а) если 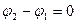, то — уравнение прямой,

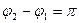
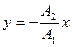
б) если , то — уравнение прямой,

в) если 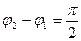, то — уравнение эллипса, приведённого к осям,

г) если и , то — уравнение окружности, где — радиус окружности.

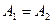
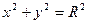
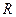
МЕХАНИЧЕСКИЕ ВОЛНЫ

· Длина волны, т.е расстояние между ближайшими частицами, колеблющимися в одинаковой фазе

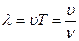
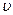
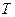
где — скорость волны, — период, — частота.

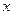
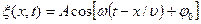
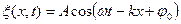
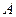
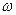
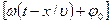
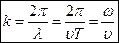
· Уравнение бегущей волны, распространяющейся вдоль положительного направления оси в среде, не поглощающей энергию,

или

, где

— амплитуда волны, — циклическая частота, -фаза волны, — начальная фаза, — волновое число.

Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Волна называется поперечной, если частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.

Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела. Продольные волны могут распространяться как в твердых телах, так и в жидких и газообразных средах.

Маятник

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.

Отклонение маятника от положения равновесия будем характеризовать углом образованным нитью с вертикалью (рис. 54.1). При отклонении маятника от положения равновесия возникает вращательный момент N, равный по величине — масса, a l — длина маятника). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписывать противоположные знаки 1). Следовательно, выражение для вращательного момента имеет вид

Напишем для маятника уравнение динамики вращательного движения. Обозначив угловое ускорение через и учитывая, что момент инерции маятника равен получаем:

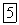
Последнее уравнение можно привести к виду

(54.2)

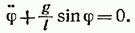
Ограничимся рассмотрением малых колебаний. В этом случае можно положить Введя, кроме того, обозначение

придем к уравнению

к зторое идентично с уравнением (53.1). Его решение имеет вид

Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону.

Как следует из (54.3), частота колебаний математического маятника зависит только от длины маятника и от ускорения силы тяжести и не зависит от массы маятника. По формуле (53.8) с учетом (54.3) получается известное из школьного курса выражение для периода колебаний математического маятника:

Отметим, что, решив уравнение (54.2), можно найти для периода колебаний следующую формулу:

где а — амплитуда колебаний, т. е. наибольший угол, на который отклоняется маятник из положения равновесия.

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m — масса маятника, а l — расстояние между точкой подвеса О и центром масс С маятника (рис. 54.2). Знак «—» имеет то же значение, что и в случае формулы (54.1).

Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать:

В случае малых колебаний (54.8) переходит в уже известное нам уравнение:

Через обозначена в данном случае следующая величина:

(54.10)

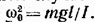
Из уравнений (54.9) и (54.10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника. В соответствии с (54.10) период колебаний физического маятника определяется выражением

(54.11)

Из сопоставления формул (54.6) и (54.11) получается, что математический маятник с длиной

(54.12)

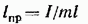
будет иметь такой период колебаний, как и данный физический маятник. Величину (54.12) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника — это длина такого математического маятника, период колебании которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.точку О на рис. 54.2).

Можно показать (рекомендуем это сделать в порядке упражнения), что при подвешивании маятника в центре качания О приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится нозым центром качания.

На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно Измерив период колебаний маятника и зная можно по формуле