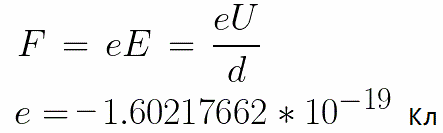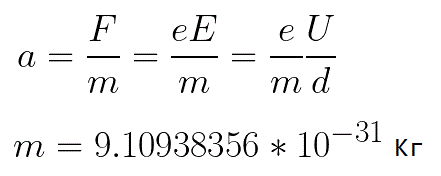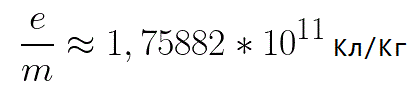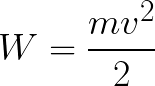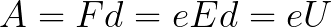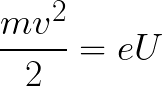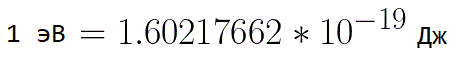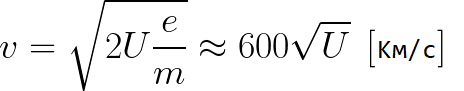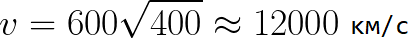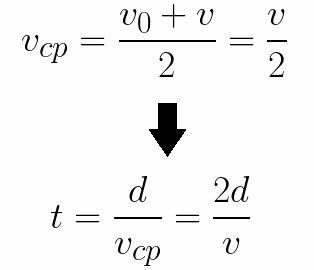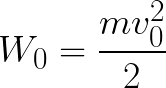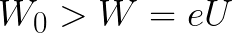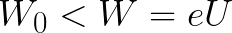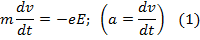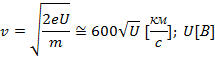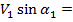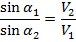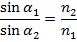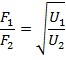Электрон в электрическом поле
Движение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле.
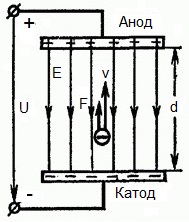
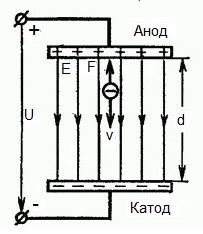
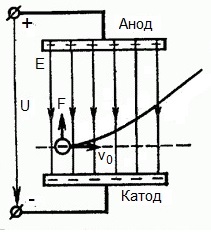
На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами.
К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля:
Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться.
Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так:
В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой:
Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна:
Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна:
Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом:
То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U.
В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина:
Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь:
Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути.
Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна:
Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно:
Теперь рассмотрим пример когда электрон движется в тормозящем однородном электрическом поле. То есть поле направлено как и прежде, но электрон начинает двигаться наоборот — от анода к катоду.
Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду.
Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле».
От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону.
Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение.
Если же начальная кинетическая энергия электрона меньше данной критической величины, то электрон не достигнет катода. В определенный момент он остановится, затем начнет равноускоренное движение обратно — к аноду. В итоге поле вернет ему энергию, которая израсходовалась в процессе торможения.
А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E.
Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду.
Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории.
Видео:Урок 227. Проводники в электрическом полеСкачать

Движение электрона в однородном электрическом поле.
В электрическом поле с напряженностью E на электрон действует сила:
Поскольку при движении в вакууме электрон не испытывает столкновений, приводящих к изменению величины и направления его скорости, то уравнение движения электрона выглядит так:
Где: 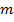



Это уравнение позволяет полностью описать движение электрона, найти его траекторию и скорость в любой точке, если известны начальные условия:
— координаты, величина и направление скорости в начале пути и если известна картина поля, т.е. заданы в виде функции координат векторы напряженности электрического поля E. Представим уравнение (1) в виде:
Проинтегрируем по пути от точки 1 до точки 2:
Электрическое поле влияет на кинетическую энергию электрона и на правление его движения. При движении в однородном электрическом поле напряженностью 



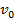

Здесь 



Если начальная скорость была невелика, то
Так если
Таким образом, приобретенная электроном энергия однозначно определяет его скорость. При скоростях электрона, близких к скорости света, во всех приведенных уравнениях должна быть учтена релятивистская масса электрона.
Релятивистский эффект нужно учитывать при анализе движения электрона, ускоряемого разностью потенциалов более 100 киловольт, как в приведённом примере.
В первом приближении можно считать массу электрона постоянной и,
что электроны ускоряются в однородном электрическом поле в межэлектродном пространстве. Однако вблизи отверстия в аноде электрическое поле неоднородно и обладает фокусирующим действием.
Движение электронов вблизи отверстия можно представить с помощью принципов «электронной оптики».
Рассмотрим прохождение заряженной частицы через границу двух эквипотенциальных областей.
Рис. 8 Прохождение заряженной частицы через границу двух эквипотенциальных областей
Предположим, что заряженная частица движется в пространстве, в котором имеется скачок потенциала на некоторой границе. Такой скачок потенциала, конечно, нельзя осуществить технически, так как ему соответствует бесконечно большая величина напряженности поля.
Наилучшим приближением будет система, состоящая из двух близко расположенных чрезвычайно тонких слоев металлической фольги (конденсатора), прозрачных для рассматриваемых частиц и заряженных до соответствующих потенциалов. Проходя через границу раздела, заряженная частица испытывает действие силы, направленной по нормали к этой границе. Поэтому нормальная составляющая скорости изменяется, а тангенциальная составляющая остается неизменной.
Последнее условие дает:
где v1 и v2 — значения скорости частицы до и после прохождения через поверхность раздела, а углы 

Если, как обычно, считать, что величина скорости частицы определяется значением потенциала в данной точке, то равенство может быть записано в следующем виде:
Написанное равенство полностью совпадает с обычной формулировкой закона преломления в оптике:
где — 

Роль коэффициента преломления играет квадратный корень из значения
потенциала в данной точке.
Рисунок 9 Преломление траектории электрона на эквипотенциальных поверхностях
Электростатическое поле всегда может быть изображено с помощью системы эквипотенциальных поверхностей (рисунок).
Если эти поверхности проведены достаточно близко друг к другу, то при рассмотрении движения частицы можно считать, что потенциал в пространстве между двумя соседними эквипотенциалями постоянен и все изменение потенциала происходит маленькими скачками на самих эквипотенциальных поверхностях. Таким образом, траектория движения электрона в неоднородном электрическом поле подобна траектории распространения светового луча в среде с переменным коэффициентом преломления.
Следует указать отличия, обычной оптики от электронной:
— в электронной оптике неосуществимы скачкообразные изменения коэффициента преломления, которые являются характерными для обычных линз;
— вследствие плавного изменения коэффициента преломления в электронной оптике электроны движутся вдоль кривых, в обычной оптике световые лучи распространяются вдоль прямых линий;
— коэффициент преломления в электронной оптике ограничен только электрической прочностью среды и может достигать 8-9, в то время, как в обычной – 1,1 – 1,4. Следовательно, оптическая сила электронных линз многократно превышает оптическую силу обычных линз.
Аналогом оптической линзы в электронной оптике служит электрическое поле, обладающее аксиальной (осевой) симметрией. Аксиально-симметричное поле может быть создано различными способами: коаксиальные цилиндры, диафрагмы с круглыми отверстиями, электроды, имеющие форму кольца. Каждая эквипотенциальная поверхность в такой системе вблизи оси будет иметь сферическую форму. Параксиальный пучок электронов (т.е. движущийся на небольшом расстоянии от оси и под малыми углами к ней), будет вести себя подобно пучку световых лучей в сложной оптической линзе, склеенной из бесконечно большого числа тонких менисков с постепенно изменяющимися коэффициентами преломления. Электростатические линзы обладают свойствами собирать (фокусировать) или рассеивать проходящие сквозь них пучки заряженных частиц. Существуют линзы различных типов. Рассмотрим действие линзы на электроны на примере иммерсионной линзы, состоящей из двух заряженных цилиндров:
Рисунок 10 Иммерсионная линза. Эквипотенциальные поверхности и изменение потенциала на оси.
Рассмотрим параксиальный пучок электронов, т.е. пучок, движущийся на небольшом расстоянии от оси и под малыми углами к ней и проходящий через зазор между двумя коаксиальными цилиндрами, потенциалы которых равны соответственно 

Рисунок 11 Иммерсионная линза, образованная двумя цилиндрами.
Электронные траектории, входящие в линзу параллельно оптической оси, пересекают ось после прохождения линзы в главных фокусах 

Силу, действующую на электрон в каждой точке его пути, можно разложить на две составляющие: параллельную оси и перпендикулярную к ней. На участке траектории до середины зазора радиальная составляющая силы направлена к оси. После прохождения через середину зазора радиальная сила стремится отклонить его от оси. Фокусирующее действие радиальной составляющей на первой половине пути не может быть скомпенсировано дефокусирующим действием на второй половине пути. Это объясняется тем, что первую часть пути электрон движется с меньшей скоростью и, следовательно, дольше находится под действием сил, прижимающей его к оси. В результате электронная траектория пересекает ось в некоторой точке 



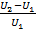
где 

Общие свойства иммерсионных линз:
— иммерсионные линзы всегда собирающие;
— иммерсионные линзы несимметричны, их фокусные расстояния 

Иммерсионная линза, создавая электронное изображение, всегда изменяет
энергию электронного пучка.
Прохождение электронного луча через отверстие в аноде можно уподобить прохождению его через иммерсионную линзу. В результате траектории большинства электронов стягиваются к центру отверстия, электроны пролетают сквозь него и попадают в пространство за анодном. Так как потенциалы анода и мишени одинаковы, электрическое поле в пространстве за анодом отсутствует, и дальнейшее движение электронов происходит по инерции. Степень фокусировки электронов электростатическим полем не велика, и диаметр луча в наименьшем сечении лежит в интервале от долей до единиц миллиметров. В дальнейшем электронный поток формируется, и фокусируются электромагнитной системой на малую площади обрабатываемой заготовки. Наименьший диаметр площади фокусировки зависит от тока луча и может составлять сотые доли миллиметра.
Видео:Электрон в электрическом полеСкачать

Тема: Определение удельного заряда электрона методом магнетрона
Тема: Определение удельного заряда электрона методом магнетрона.
Цель работы: познакомиться с законами движения заряженных частиц в электрическом и магнитном полях, определить удельный заряд электрона с помощью цилиндрического магнетрона.
Краткие теоретические сведения: магнетроном называется электро-вакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.

При этом силовые линии электрического поля имеют радиальное направление, а линии магнитной индукции совпадают с осью электродов (рис.2).
Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:

где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.
Траектория движения заряженной частицы в электромагнитном поле существенно зависит от величины удельного заряда — отношения заряда к массе частицы. Уравнение траектории можно получить из решения уравнения (1), но даже в случае цилиндрической симметрии это уравнение не имеет решения в аналитическом виде.
Рассмотрим на качественном уровне движение электрона в цилиндрическом магнетроне. Для упрощения предположим, что электроны вылетают из катода с нулевой начальной скоростью, их движение происходит в плоскости, перпендикулярной оси электродов, а радиус катода много меньше радиуса анода.
При протекании тока в цепи накала, в результате термоэлектронной эмиссии с катода, в лампе образуются свободные электроны. Эмитированные катодом электроны под действием электрического поля движутся к аноду, и в анодной цепи возникает электрический ток. Постоянный ток в обмотке соленоида создает магнитное поле, искривляющее траекторию движения электронов.
Выясним характер движения электронов в магнетроне. В электрическом поле на электрон действует сила F = eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

где Ua — анодное напряжение лампы.
В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

Отсюда выразим радиус окружности:


Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод, как на рис 3в. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода

где значение скорости в соответствии с формулой (2) равно

Анодный ток при этом прекращается.
Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (5) и (6) можно рассчитать удельный заряд электрона:

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода, как показано на рис. 3г.
Для определения удельного заряда электрона по формуле (7) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением

где N — число витков, l — длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:




Соленоид подключается к источнику постоянного напряжения, а ток соленоида фиксируется амперметром. Справа изображены источник напряжения и приборы, регистрирующие параметры анодной цепи.
Подаем на лампу анодное напряжение 20В. Получили значение анодного тока Іа=0,5834.
Изменяя силу тока в соленоиде, снимаем зависимость анодного тока от тока соленоида. Данные заносим в таблицу:
По данным таблицы построим зависимость анодного тока от тока соленоида.
Графически продифференцируем эту зависимость и определим критическое значение тока соленоида. Максимум построенной функции соответствует критической силе тока в соленоиде.
Таким образом, критическое значение тока соленоида составляет Іс(кр)=320А.
По формуле 
Выводы: в выполненной работе мы познакомились с законами движения заряженных частиц в электрическом и магнитном полях, определили удельный заряд электрона с помощью цилиндрического магнетрона.
1. Что такое магнетрон и как он работает?
Ответ: Магнетроном называется электровакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.
В работе магнетрона используется процесс движения электронов при наличии двух полей — магнитного и электрического, перпендикулярных друг другу. Магнетрон представляет собой двухэлектродную лампу или диод, содержащий накаливаемый катод, испускающий электроны, и холодный анод. Магнетрон помещается во внешнее магнитное поле. Анод (анодный блок) магнетрона имеет довольно сложную монолитную конструкцию с системой резонаторов, необходимых для усложнения структуры электрического поля внутри магнетрона. Магнитное поле создается либо катушками с током (электромагнит), либо постоянным магнитом, между полюсами которого помещается магнетрон. Если бы магнитного поля не было, то электроны, вылетающие из катода практически без начальной скорости, двигались бы в электрическом поле вдоль прямых 
Траектория электрона есть циклоида, описываемая точкой, лежащей на окружности круга, равномерно катящегося по катоду. При прохождении циклоидного потока электронов мимо щелей резонаторов анодного блока, в них возбуждаются мощные электромагнитные СВЧ колебания. Высокочастотная энергия из прибора обычно выводится с помощью петли или отверстия связи, помещенных в периферийной части одного из резонаторов анодного блока.
Магнетрон разрабатывался как мощный генератор электромагнитных колебаний СВЧ диапазона для использования в системах РЛС. Эффект нагревания предметов микроволнами нашел применение в микроволновых (СВЧ) печах.
2. Изобразите направление электрического и магнитного полей в магнетроне и траектории движения электронов.
Ответ: В магнетроне электрон движется в скрещенных электрическом и магнитном полях. В отсутствии магнитного поля траектории движения электронов приведены на рис. 3а. При наложении «слабого» магнитного поля траектории электронов искривляются, но все электроны долетают до анода, как показано на рис. 3б.
3. Какие силы действуют на электрон в магнетроне? Укажите направление сил, действующих на электрон в магнетроне. Запишите второй закон Ньютона для электрона в магнетроне.

Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:
где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.
4. Сделайте вывод рабочей формулы.
Ответ: в электрическом поле на электрон действует сила F=eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

где Ua — анодное напряжение лампы. В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

Отсюда выразим радиус окружности:

Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода:

где значение скорости в соответствии с формулой (1) равно:

Анодный ток при этом прекращается.
Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (4) и (5) можно рассчитать удельный заряд электрона

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода.
Для определения удельного заряда электрона по формуле (6) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением:


где N-число витков, l-длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:
5. Какие графики нужно построить в данной работе? Поясните ход экспериментальных кривых.
Ответ: в данной лабораторной работе нужно построить график зависимости анодного тока от тока соленоида и график зависимости скорости изменения анодного тока от тока соленоида. Первый график показывает, что при увеличении тока соленоида и соответственно значения вектора магнитной индукции анодный ток прекращается, т. к. радиус движения электронов уменьшается, и они не достигают анода. Второй график позволяет определить ток соленоида, при котором электроны перестают долетать до анода.
1. Савельев общей физики, 1978, т2, §§50,72
📹 Видео
Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

ФИЗИКА 8 класс : Электрическое поле | ВидеоурокСкачать

Электрическое поле. Откуда берется ток.Скачать

Электрон в электрическом полеСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Урок 137 (осн). Электрическое поле. Делимость электрического заряда. Опыт Милликена-ИоффеСкачать

Электростатика, движение электрона в электрическом полеСкачать

Диэлектрики в электрическом полеСкачать

Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Проводники и диэлектрики. Делимость электрических зарядов | Физика 8 класс #9 | ИнфоурокСкачать

Все виды движения в электрическом поле | Физика ЕГЭ 2023 | УмскулСкачать

Электрический ток в металлахСкачать
Движение электронов в атоме. 1 часть. 8 класс.Скачать

Урок 280. Подготовка к контрольной работеСкачать

Физика - Магнитное полеСкачать