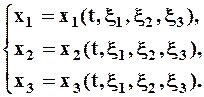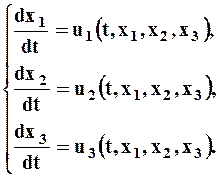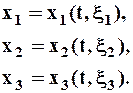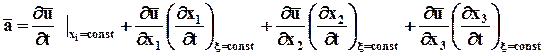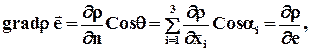2017-05-07 
Частица движется в плоскости $xy$ с постоянным ускорением $vec$, направление которого противоположно положительному направлению оси $y$. Уравнение траектории частицы имеет вид $y = ax — bx^$, где $a$ и $b$ — положительные постоянные. Найти скорость частицы в начале координат.
В соответствии с проблемой $vec = w (- vec)$
Дифференцируя уравнение траектории, $y = ax — bx^$, по времени
Получаем, $left . frac
Опять дифференцируя по времени
или, $- w = a(0) — 2b left ( frac
Используя (3) в (2) $left . frac
Следовательно, скорость частицы в начале координат
Видео:Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Траектория движения
Видео:кинематика точкиСкачать

Определение и основные понятия траектории движения
Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория — кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение траектории движения
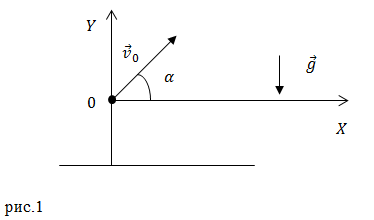
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
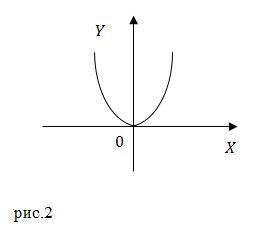
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.
Видео:Кинематика точки Задание К1Скачать

Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
- Третьим способом описания движения является описание с помощью параметров траектории.
Путь — это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Примеры задач с решением
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit
Решение: Рассмотрим уравнение изменения скорости частицы:
Из этого уравнения следует, что:
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
Видео:Физика элементарных частиц – курс Дмитрия Казакова / ПостНаукаСкачать

МЕТОДЫ ОПИСАНИЯ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
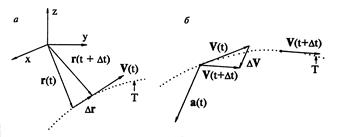 Рис. 3.1. Скорость и ускорение материальной точки. Пунктиром показана её траектория Рис. 3.1. Скорость и ускорение материальной точки. Пунктиром показана её траектория |
При изучении движения сплошной среды можно также выделить бесконечно малые объёмы, положение которых характеризуется в пространстве тремя координатами или величиной одного радиус-вектора 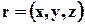
Метод Лагранжа. Обозначим координаты начального (в момент времени 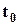
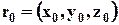
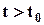
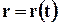
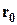
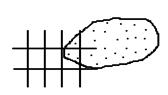 Рис.3.2. Задание координат методом Лагранжа Рис.3.2. Задание координат методом Лагранжа |
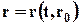
Такой подход к описанию движения сплошной среды называется методом Лагранжа, а характеристики сплошной среды (скорость, плотность, давление и т.п.), связанные с движущимися элементарными объёмами сплошной среды, равно как и координаты этого объёма, называются лагранжевыми переменными.
Лагранжевы координаты — это параметры, которые характеризуют каждую точку среды и не меняются в процессе. Таким образом, точка зрения Лагранжа опирается на описание истории движения каждой точки сплошной среды в отдельности. Такое описание на практике оказывается слишком подробным и сложным, оно всегда подразумевается при формулировке физических законов.
Используя равенства, введённые в теоретической механике
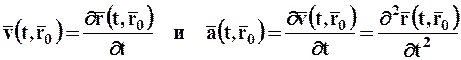
можно вычислить скорость и ускорение каждой частицы, а затем, определив величину внешних (поверхностных и объёмных) сил, действующих на каждую частицу, записать уравнения движения для сплошной среды.
Несмотря на кажущуюся простоту метода Лагранжа, уравнения движения, получаемые на основе этого метода, очень сложны, и он используется сравнительно редко.
Более удобен и потому гораздо шире используется другой подход к описанию движения сплошной среды, называемый методом Эйлера.
Согласно этому методу фиксируют не частицы жидкости, а точки пространства, через которые проходят в разные моменты времени различные элементарные объёмы жидкости, т.е. жидкие частицы. В этих точках определяются значения скорости движения сплошной среды. Таким образом, средством описания движения сплошной среды является поле скорости движения жидких частиц в фиксированных точках пространства:
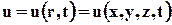
Характеристики сплошной среды (поле скорости, поле давлений, поле напряжений и т.п.), отнесённые к фиксированным неподвижным элементам геометрического пространства (точкам, линиям, поверхностям, объёмам), и сами эти элементы называют эйлеровыми переменными.
Этот метод удобен благодаря следующим преимуществам.
· Во-первых, наблюдать за движущимися (например, в трубе) фиксированными (мечеными) жидкими частицами значительно сложнее, чем за характеристиками движения сплошной среды.
· Во-вторых, соответствующие этому методу уравнения оказываются проще для анализа.
Подчеркнём, что, если в методе Лагранжа 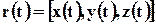
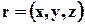
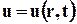
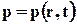
Учитывая, что в методе Эйлера описание движения отличается от принятого в теоретической механике, существуют некоторые отличия в определении ускорения, которое входит во второй закон Ньютона. В это уравнение входит ускорение материальной точки, которое для сплошной среды определяется, как и в теоретической механике, второй производной пути по времени только при использовании метода Лагранжа. В случае метода Эйлера ускорение, а также другие гидромеханические величины, которые меняются вместе с движением объёма жидкости, выражаются через специальный вид производной, которая определённым образом связана с полем скорости (3.2.2). Вместе с тем эта производная должна быть связана с движением частиц жидкости или газа (субстанции). Такую производную называют полной или субстанциальной.
Скорость. Пусть некоторая точка сплошной среды в момент t находится в точке М пространства, а в момент t + Dt в точке M´, и 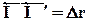
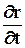
Радиус-вектор r зависит в общем случае от трёх параметров x, y, z , индивидуализирующих точку сплошной среды, и времени t. Скорость вычисляется для индивидуальной точки сплошной среды, т.е. при фиксированных x, y, z , поэтому и берётся частная производная от rпо t: 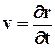
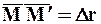
Dr = Dx×i + Dy×j + Dz×k,
где Dx, Dy, Dz являются компонентами перемещения Dr.Или, переписывая в обобщённом и сокращённом виде, будем иметь
Dr = S Dx i еi = Dx i еi (*)
(В последнем выражении знак суммы опущен).
Поделив (*) на элемент времени Dt,соответствующий перемещению точки сплошной среды из точки Мв точку M´ пространства наблюдателя, и взяв предел при Dt® 0, получим по определению скорость точки сплошной среды : 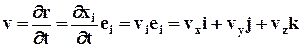
откуда 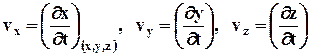
индексы 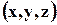
vx = vx (x, y, z, t),
vy = vy (x, y, z, t),
vz = vz (x, y, z, t).
Запишем проекции скоростей и ускорений точек среды на обобщённые оси координат хi, которые определяются обычными равенствами:
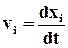
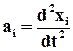
Таким образом, в методе Эйлера задаются перемещение, скорость, ускорение в точке пространства (неподвижная система отсчёта), мимо которой в данный момент проходят частицы среды как функции координат точек пространства xi и времени t:
Совокупность параметров хi и tназывают переменными Эйлера.
Ввиду того, что в механике сплошной среды могут встретиться оба метода, необходимо научиться осуществлять переход от одних переменных к другим.
Переход от переменных Лагранжа к переменным Эйлера.Предположим, что у нас всё известно о среде с точки зрения Лагранжа, то есть, мы имеем 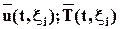
Для того, чтобы перейти к переменным Эйлера нам необходимо:
· разрешить уравнения относительно xi. При фиксированных координатах хi эти соотношения указывают те точки xi сплошной среды, которые в разные моменты времени проходят через данную точку пространства.
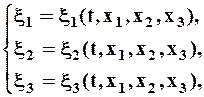
· подставить это в выражения по Эйлеру:
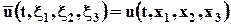
 Рис. 3.3. Переход от координат Эйлера к координатам Лагранжа Рис. 3.3. Переход от координат Эйлера к координатам Лагранжа |
Для перехода от переменных Эйлера к переменным Лагранжаимеем:
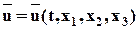
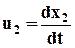
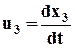
Для начальных условий при t = 0:
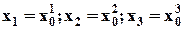
· получим систему обыкновенных дифференциальных уравнений относительно хi: 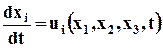
· Решая эту систему, определим хi = хi(С1, С2, С3, t),где — С1, С2, С3-постоянные, определяемые по хi при t = t0;
· подставив (**) в (*),получим лагранжевы координаты.
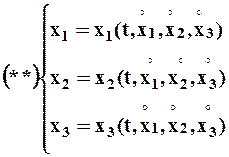
Ускорение и его вычисление по скорости.Ускорение – это скорость изменения скорости индивидуальной частицы. Если скорость задана по Лагранжу, т.е.
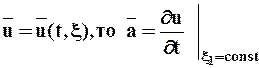
Если скорость задана по Эйлеру, то 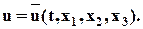
Поэтому 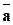
Окончательная формула по Эйлеру будет выглядеть:
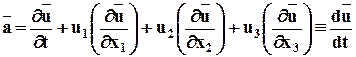
Это полная (материальная) производная скорости по времени, индивидуальная производная по времени, субстанциальная производная.
По Эйлеру 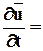
Если 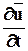
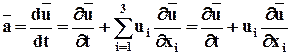
В декартовых координатах x,y,z:
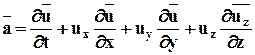
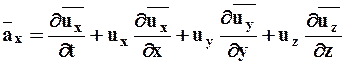
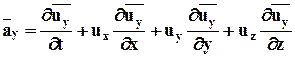
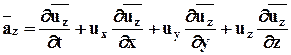
Материальная (полная) или индивидуальная производная по t от любой величины (например, плотности r) определится следующим образом:
· Если используется способ Лагранжа, т.е. если 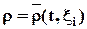
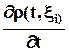
· Если используется способ Эйлера, т.е. 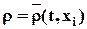
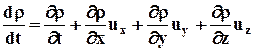
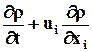
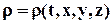
Для несжимаемой среды 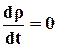

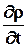
Таким образом, если функция задана в переменных Эйлера: r = r (x1, x2, x3, t), необходимо
· перейти к переменным Лагранжа;
· воспользоваться правилом дифференцирования сложной функции, в результате чего получим
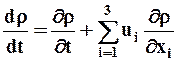
Производная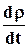
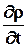
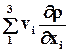
Рассмотрим полную производную по времени от температуры. По Эйлеру это будет выглядеть следующим образом:
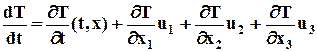
Физический смысл (по Эйлеру) – это производная температуры по времени в какой-либо фиксированной точке пространства x = const. В координатах Лагранжа 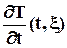
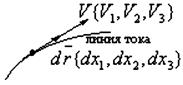 Рис.3.4. Векторные линии или линии тока Рис.3.4. Векторные линии или линии тока |
Линия тока и траектория. Линией тока в поле скорости сплошной среды (в фиксированный момент времени) называется такая кривая, в каждой точке которой вектор скорости направлен по касательной к ней. Линия тока является эйлеровой характеристикой потока; её не следует отождествлять с траекторией — геометрическим местом последовательных положений материальной точки (элементарной жидкой частицы) при её движении в пространстве, которая является лагранжевой характеристикой потока. Траектория — это путь индивидуальной частицы. Поэтому эти линии совпадают только при установившемся движении, когда поле скорости не меняется во времени, т.е. u = u (r). Если же движение неустановившееся, u = u(r,t), то эти линии не совпадают.
Важной особенностью совокупности линий тока в фиксированный момент времени является то, что они никогда не пересекаются друг с другом, за исключением особых точек (например, в случае источника — фонтана). Это следует из того, что скорость в данной точке не может быть касательной одновременно к двум пересекающимся кривым.
 Рис. 3.5. Траектория движения частицы Рис. 3.5. Траектория движения частицы |
Если элементарный вектор, касательный к линии тока, обозначить через 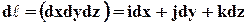
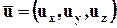
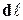
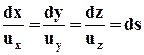
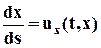
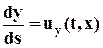
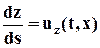
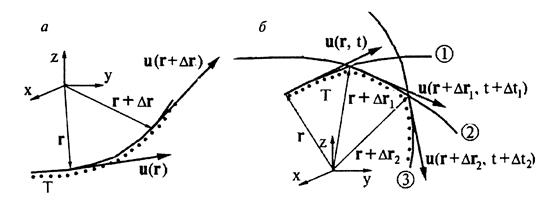 Рис.3.6. Линии тока и траектории: а — при установившемся движении совпадают; б — при неустановившемся движении 1,2.3 — линии тока в моменты времени t, t + Dt1, t + Dt2. Т — траектории элементарного жидкого объёма показаны пунктиром Рис.3.6. Линии тока и траектории: а — при установившемся движении совпадают; б — при неустановившемся движении 1,2.3 — линии тока в моменты времени t, t + Dt1, t + Dt2. Т — траектории элементарного жидкого объёма показаны пунктиром |
Особенности лагранжева и эйлерова методов описания движения сплошной среды продемонстрируем на примере установившегося движения жидкости (рис.3.6), при котором траектория и линия тока совпадают.
При лагранжевом методе (рис.3.4,а) жидкая частица, имеющая при t = t0 начальную координату r0 = (x0, y0, z0), движется по траектории, занимая в моменты времени t0, t0 +Dt, t0 + 2Dt, t0 + 3Dt положения в пространстве, отмеченные на рисунке точками, то есть в параметрическом виде будем иметь 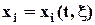
Скорость этой частицы изменяется со временем; картина течения представляется набором траекторий различных частиц жидкости. При эйлеровом подходе тот же поток (рис.3.6,б) описывается полем скорости u = u(r,t); при установившемся движении, когда 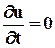
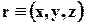
Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую её точку провести линию тока, то образуется поверхность тока. Если кривая С замкнута, поверхность тока превращается в трубку тока.
Аналитически семейство линий тока в проекциях выглядит следующим образом:
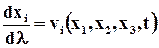
Где dl — скалярный параметр. Выражение (3.2.8) – это дифференциальные уравнения линий тока.
Они отличаются от уравнений, описывающих закон движения или траектории движения частиц сплошной среды:
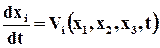
тем, что в уравнениях (3.2.8) t –параметр, а в(3.2.9) t — переменная величина.
Итак, линии тока не совпадают с траекториями. Совпадать они могут только в двух случаях:
1. При установившихся движениях (тогда между двумя последними уравнениями нет различия).
2. При неустановившихся течениях (когда поле скоростей меняется по величине, но не меняется по направлению).
Если какая-либо скалярная величина задана как функция переменных Эйлера, то в каждый момент времени можно рассматривать
Эта поверхность называется поверхностью равного уровня или эквипотенциальной поверхностью. Вектор, направленный по нормали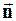
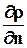
Вектор-градиент обозначается как grad r и вычисляется по формуле:
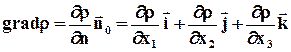
где 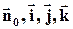
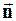
Проекция вектора grad r на некоторое направление 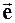
где q — угол между направлениями 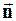
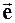
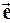
Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (3.2.10).
📹 Видео
Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Кинематика точки в плоскости. ТермехСкачать

Рубцов А. Н. - Введение в квантовую физику - Частица в потенциальной ямеСкачать

Халилов В. Р. - Теоретическая механика - Задача КеплераСкачать

ЧК_МИФ_ФМЛ_30 . УРАВНЕНИЕ ДВИЖЕНИЯ ДЛЯ КЛАССИЧЕСКОЙ ЧАСТИЦЫСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точкиСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать
Теоретическая механика. Лекция №8. Рассеяние частицСкачать

Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Теория поля 5. Четырехмерное уравнение движения. Тензор ЭМ поля. 1-ая пара уравнений МаксвеллаСкачать