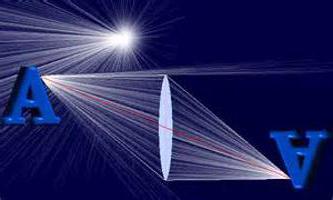
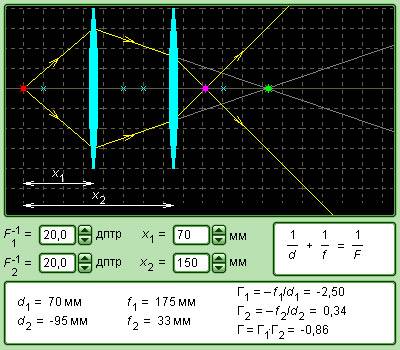
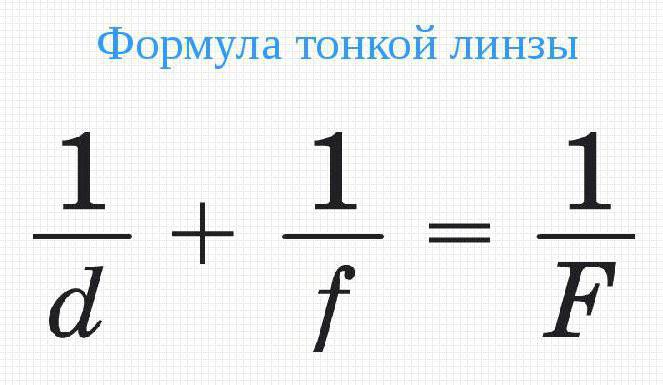Сейчас речь пойдет о геометрической оптике. В этом разделе много времени уделяется такому объекту, как линза. Ведь она может быть разной. При этом формула тонкой линзы одна на все случаи. Только нужно знать, как ее правильно применить.
- Виды линз
- Общие характеристики
- Какие еще обозначения есть в формуле тонкой линзы
- Что нужно для построения изображения в тонкой линзе
- Как построить изображение в тонкой линзе
- Вывод формулы тонкой линзы
- Задача о нахождении увеличения линзы
- Задача, в которой нужно найти фокус
- Задача о нахождении расстояния до изображения
- Задача о расстоянии между предметом и его изображением
- Вместо заключения
- Тонкие линзы
- Построение изображения в линзах
- Астрономическая труба Кеплера и земная труба Галилея
- Что представляет собой фотоаппарат
- Формула тонкой линзы
- теория по физике 🧲 оптика
- Вывод формулы
- Увеличение линзы
- 📽️ Видео
Видео:Линзы, оптическая сила линзы, формула тонкой линзы.Построение изображений в линзах. 8 класс.Скачать

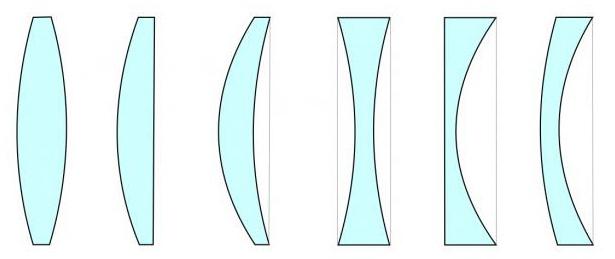
Виды линз
Ею всегда является прозрачное для световых лучей тело, которое имеет особенную форму. Внешний вид объекта диктуют две сферические поверхности. Одну из них допускается заменить на плоскую.
Причем у линзы может оказаться толще середина или края. В первом случае она будет называться выпуклой, во втором — вогнутой. Причем в зависимости от того, как сочетаются вогнутые, выпуклые и плоские поверхности, линзы тоже могут быть разными. А именно: двояковыпуклыми и двояковогнутыми, плосковыпуклыми и плосковогнутыми, выпукло-вогнутыми и вогнуто-выпуклыми.
В обычных условиях эти объекты используются в воздухе. Изготавливают их из вещества, оптическая плотность которого больше, чем у воздуха. Поэтому выпуклая линза будет собирающей, а вогнутая — рассеивающей.
Видео:Линзы, оптическая сила линзы, формула тонкой линзы.Построение изображений в линзах. 8 класс.Скачать

Общие характеристики
До того, как говорить о формуле тонкой линзы , нужно определиться с основными понятиями. Их обязательно нужно знать. Поскольку к ним постоянно будут обращаться различные задачи.
Главная оптическая ось — это прямая. Она проведена через центры обеих сферических поверхностей и определяет место, где находится центр линзы. Существуют еще дополнительные оптические оси. Они проводятся через точку, являющуюся центром линзы, но не содержат центры сферических поверхностей.
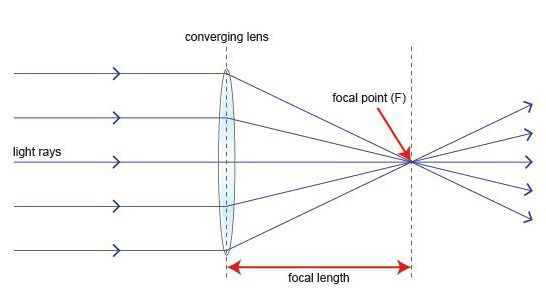
В формуле тонкой линзы есть величина, определяющая ее фокусное расстояние. Так, фокусом является точка на главной оптической оси. В ней пересекаются лучи, идущие параллельно указанной оси.
Причем фокусов у каждой тонкой линзы всегда два. Они расположены по обе стороны от ее поверхностей. Оба фокуса у собирающей действительные. У рассеивающей — мнимые.
Расстояние от линзы до точки фокуса — это фокусное расстояние (буква F ) . Причем его значение может быть положительным (в случае собирающей) или отрицательным (для рассеивающей).
С фокусным расстоянием связана еще одна характеристика — оптическая сила. Ее принято обозначать D. Ее значение всегда — величина, обратная фокусу, то есть D = 1/ F. Измеряется оптическая сила в диоптриях (сокращенно, дптр).
Видео:Формула тонкой линзы наглядно! Как понять оптику?Скачать

Какие еще обозначения есть в формуле тонкой линзы
Помимо уже указанного фокусного расстояния, потребуется знать несколько расстояний и размеров. Для всех видов линз они одинаковые и представлены в таблице.
| Обозначение | Название |
| d | расстояние до предмета |
| h | высота изучаемого предмета |
| f | расстояние до изображения |
| H | высота получившегося изображения |
Все указанные расстояния и высоты принято измерять в метрах.
В физике с формулой тонкой линзы связано еще понятие увеличения. Оно определяется как отношение размеров изображения к высоте предмета, то есть H/h . Его можно обозначить буквой Г.
Видео:Урок 397. Формула тонкой линзы. Линейное увеличение линзыСкачать

Что нужно для построения изображения в тонкой линзе
Это необходимо знать, чтобы получить формулу тонкой линзы, собирающей или рассеивающей. Чертеж начинается с того, что обе линзы имеют свое схематическое изображение. Обе они выглядят как отрезок. Только у собирающей на его концах стрелки направлены наружу, а у рассеивающей — внутрь этого отрезка.
Теперь к этому отрезку необходимо провести перпендикуляр к его середине. Так будет изображена главная оптическая ось. На ней с обеих сторон от линзы на одинаковом расстоянии полагается отметить фокусы.
Предмет, изображение которого требуется построить, рисуется в виде стрелки. Она показывает, где находится верх предмета. В общем случае предмет помещается параллельно линзе.
Видео:26 задание ЕГЭ | Формула тонкой линзы | Собирающая линза | ЕГЭ по физике 2023Скачать

Как построить изображение в тонкой линзе
Для того чтобы построить изображение предмета, достаточно найти точки концов изображения, а потом их соединить. Каждая из этих двух точек может получиться от пересечения двух лучей. Наиболее простыми в построении являются два из них.
Идущий из указанной точки параллельно главной оптической оси. После соприкосновения с линзой он идет через главный фокус. Если речь идет о собирающей линзе, то этот фокус находится за линзой и луч идет через него. Когда рассматривается рассеивающая, то луч нужно провести так, чтобы его продолжение проходило через фокус перед линзой.
Идущий непосредственно через оптический центр линзы. Он не изменяет за ней своего направления.
Бывают ситуации, когда предмет поставлен перпендикулярно главной оптической оси и заканчивается на ней. Тогда достаточно построить изображение точки, которая соответствует краю стрелки, не лежащей на оси. А потом провести из нее перпендикуляр к оси. Это и будет изображение предмета.
Пересечение построенных точек дает изображение. В тонкой собирающей линзе получается действительное изображение. То есть оно получается непосредственно на пересечении лучей. Исключением является ситуация, когда предмет помещен между линзой и фокусом (как в лупе), тогда изображение оказывается мнимым. У рассеивающей же оно всегда получается мнимым. Ведь оно получается на пересечении не самих лучей, а их продолжений.
Действительное изображение принято чертить сплошной линией. А вот мнимое — пунктиром. Связано это с тем, что первое на самом деле там присутствует, а второе только видится.
Видео:Линза. Построение изображений в линзе. Формула тонкой линзы | Физика 11 класс #29 | ИнфоурокСкачать

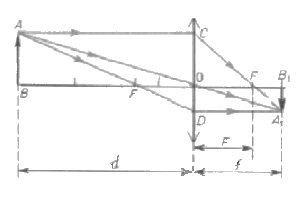
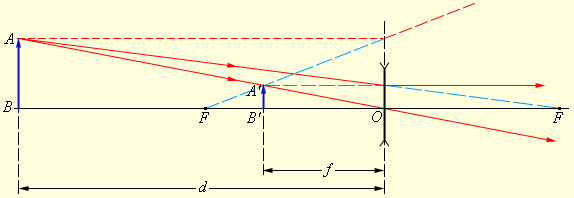
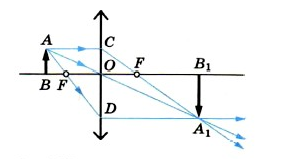
Вывод формулы тонкой линзы
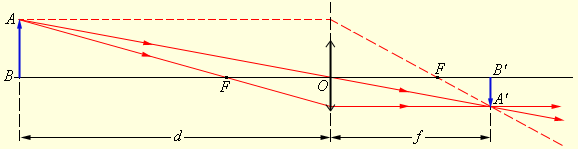
Это удобно сделать на основе чертежа, иллюстрирующего построение действительного изображения в собирающей линзе. Обозначение отрезков указано на чертеже.
Раздел оптики не зря называется геометрической. Потребуются знания именно из этого раздела математики. Для начала необходимо рассмотреть треугольники АОВ и А 1 ОВ 1 . Они подобны, поскольку в них имеется по два равных угла (прямые и вертикальные). Из их подобия следует, что модули отрезков А 1 В 1 и АВ относятся как модули отрезков ОВ 1 и ОВ.
Подобными (на основании того же принципа по двум углам) оказываются еще два треугольника: COF и A 1 FB 1 . В них равны отношения уже таких модулей отрезков: А 1 В 1 с СО и FB 1 с OF. Исходя из построения равными будут отрезки АВ и СО. Поэтому левые части указанных равенств отношений одинаковые. Поэтому равны и правые. То есть ОВ 1 / ОВ равно FB 1 / OF.
В указанном равенстве отрезки, обозначенные точками, можно заменить на соответствующие физические понятия. Так ОВ 1 — это расстояние от линзы до изображения. ОВ является расстоянием от предмета до линзы. OF — фокусное расстояние. А отрезок FB 1 равен разности расстояния до изображения и фокуса. Поэтому его можно переписать по-другому:
f / d = ( f – F ) / F или Ff = df – dF.
Для вывода формулы тонкой линзы последнее равенство необходимо разделить на dfF. Тогда получается:
Это у есть формула тонкой собирающей линзы. У рассеивающей фокусное расстояние отрицательное. Это приводит к изменению равенства. Правда, оно незначительное. Просто в формуле тонкой рассеивающей линзы стоит минус перед отношением 1/ F. То есть:
Видео:8 класс, 29 урок, Линзы. Построение изображений в линзахСкачать

Задача о нахождении увеличения линзы
Условие. Фокусное расстояние собирающей линзы равно 0,26 м. Требуется вычислить ее увеличение, если предмет находится на расстоянии 30 см.
Решение. Его начать стоит с введения обозначений и перевода единиц в Си. Так, известны d = 30 см = 0,3 м и F = 0,26 м. Теперь нужно выбрать формулы, основная из них та, которая указана для увеличения, вторая — для тонкой собирающей линзы.
Их нужно как-то объединить. Для этого придется рассмотреть чертеж построения изображения в собирающей линзе. Из подобных треугольников видно, что Г = H/h = f/d. То есть для того, чтобы найти увеличение, придется вычислить отношение расстояния до изображения к расстоянию до предмета.
Второе известно. А вот расстояние до изображения полагается вывести из формулы, указанной ранее. Получается, что
Теперь эти две формулы необходимо объединить.
Г = dF / ( d ( d — F )) = F / ( d — F ).
В этот момент решение задачи на формулу тонкой линзы сводится к элементарным расчетам. Осталось подставить известные величины:
Г = 0,26 / (0,3 — 0,26) = 0,26 / 0,04 = 6,5.
Ответ: линза дает увеличение в 6,5 раз.
Видео:Формула тонкой линзыСкачать

Задача, в которой нужно найти фокус
Условие. Лампа расположена в одном метре от собирающей линзы. Изображение ее спирали получается на экране, отстоящем от линзы на 25 см. Вычислите фокусное расстояние указанной линзы.
Решение. В данные полагается записать такие величины: d =1 м и f = 25 см = 0,25 м. Этих сведений достаточно, чтобы из формулы тонкой линзы вычислить фокусное расстояние.
Так 1/ F = 1/1 + 1/0,25 = 1 + 4 = 5. Но в задаче требуется узнать фокус, а не оптическую силу. Поэтому остается только разделить 1 на 5, и получится фокусное расстояние:
Ответ: фокусное расстояние собирающей линзы равно 0,2 м.
Видео:Линзы, оптическая сила линзы, формула тонкой линзы.Построение изображений в линзах.Прак.ч. 8 класс.Скачать

Задача о нахождении расстояния до изображения
Условие. Свечку поставили на расстоянии 15 см от собирающей линзы. Ее оптическая сила равна 10 дптр. Экран за линзой поставлен так, что на нем получается четкое изображение свечи. Чему равно это расстояние?
Решение. В краткую запись полагается записать такие данные: d = 15 см = 0,15 м, D = 10 дптр. Формулу, выведенную выше, нужно записать с небольшим изменением. А именно, в правой части равенства поставить D вместо 1/ F.
После нескольких преобразований получается такая формула для расстояния от линзы до изображения:
Теперь необходимо подставить все числа и сосчитать. Получается такое значение для f: 0,3 м.
Ответ: расстояние от линзы до экрана равно 0,3 м.
Видео:Лаб. раб. по теме: "Определение фокусного расстояния и оптической силы собирающей линзы" (Физика 9)Скачать

Задача о расстоянии между предметом и его изображением
Условие. Предмет и его изображение отстоят друг от друга на 11 см. Собирающая линза дает увеличение в 3 раза. Найти ее фокусное расстояние.
Решение. Расстояние между предметом и его изображением удобно обозначить буквой L = 72 см = 0,72 м. Увеличение Г = 3.
Здесь возможны две ситуации. Первая — предмет стоит за фокусом, то есть изображение получается действительное. Во второй — предмет между фокусом и линзой. Тогда изображение с той же стороны, что и предмет, причем мнимое.
Рассмотрим первую ситуацию. Предмет и изображение находятся по разные стороны от собирающей линзы. Здесь можно записать такую формулу: L = d + f. Вторым уравнением полагается записать: Г = f / d. Необходимо решить систему этих уравнений с двумя неизвестными. Для этого заменить L на 0,72 м, а Г на 3.
Из второго уравнения получается, что f = 3 d. Тогда первое преобразуется так: 0,72 = 4 d. Из него легко сосчитать d = 0, 18 (м). Теперь легко определить f = 0,54 (м).
Осталось воспользоваться формулой тонкой линзы, чтобы вычислить фокусное расстояние. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (м). Это ответ для первого случая.
Во второй ситуации — изображение мнимое, и формула для L будет другой: L = f — d. Второе уравнение для системы будет тем же. Аналогично рассуждая, получим, что d = 0, 36 (м), а f = 1,08 (м). Подобный расчет фокусного расстояния даст такой результат: 0,54 (м).
Ответ: фокусное расстояние линзы равно 0,135 м или 0,54 м.
Видео:Урок 214 (осн). Задачи на формулу тонкой линзы - 1Скачать

Вместо заключения
Ход лучей в тонкой линзе — это важное практическое приложение геометрической оптики. Ведь их используют во многих приборах от простой лупы до точных микроскопов и телескопов. Поэтому знать о них необходимо.
Выведенная формула тонкой линзы позволяет решать множество задач. Причем она позволяет делать выводы о том, какое изображение дают разные виды линз. При этом достаточно знать ее фокусное расстояние и расстояние до предмета.
Видео:Линзы,формула тонкой линзы,построение изображения в линзах.(8,11 класс)Скачать

Тонкие линзы
Линза – это прозрачное тело, имеющая 2 сферические поверхности. Она, является тонкой, если ее толщина меньше радиусов кривизны сферических поверхностей.
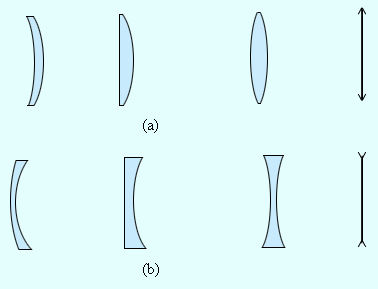
Линза — это составляющая часть почти каждого оптического прибора. Линзы бывают по своему определению собирающие и рассеивающие (рис. 3 . 3 . 1 ).
Собирающая линза — это линза, которая в середине толще, чем по краям.
Линза, имеющая большую толщину по краям, называется рассеивающей.
Рисунок 3 . 3 . 1 . Собирающие ( a ) и рассеивающие ( b ) линзы и их условные обозначения.
Главная оптическая ось – это прямая, которая проходит через центры кривизны O 1 и O 2 сферических поверхностей.
В тонкой линзе главная оптическая ось пересекается в одной точке – оптическом центре линзы O . Световой луч проходит через оптический центр линзы, не отклоняясь от своего первоначального направления.
Побочные оптические оси – это прямые, проходящие через оптический центр.
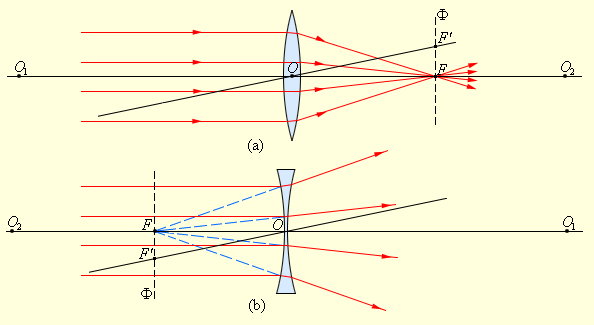
Если к линзе направить пучок лучей, которые расположены параллельно главной оптической оси, тогда после прохождения через линзу лучи (либо их продолжения) сосредоточатся в одной точке F .
Эта точка получила название главный фокус линзы.
Тонкая линза имеет два главных фокуса, которые располагаются симметрично на главной оптической оси по отношению к линзе.
Фокус собирающей линзы – действительный, а у рассеивающей – мнимый.
Пучки лучей, параллельные одной из всей совокупности побочных оптических осей, после прохождения через линзу тоже нацелены на точку F ‘ , расположенную на пересечении побочной оси с фокальной плоскостью Ф .
Фокальная плоскость – это плоскость, перпендикулярная главной оптической оси и проходящая через главный фокус (рис. 3 . 3 . 2 ).
Расстояние между главным фокусом F и оптическим центром линзы О , называется фокусным ( F ) .
Рисунок 3 . 3 . 2 . Преломление параллельного пучка лучей в собирающей ( a ) и рассеивающей ( b ) линзах. O 1 и O 2 – центры сферических поверхностей, O 1 O 2 – главная оптическая ось, О – оптический центр, F – главный фокус, F ‘ – фокус, O F ‘ – побочная оптическая ось, Ф – фокальная плоскость.
Главным свойством линз является способность передавать изображения предметов. Они, в свою очередь, бывают:
- Действительные и мнимые;
- Прямые и перевернутые;
- Увеличенные и уменьшенные.
Видео:Формула тонкой линзы | 26 задание ЕГЭ | Рассеивающая линза | Оптика 11 классСкачать

Построение изображения в линзах
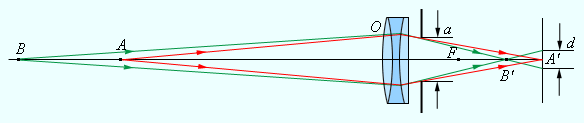
Геометрические построения помогают определить положение изображения, а также его характер. Для этой цели применяют свойства стандартных лучей, направление которых определено. Это лучи, которые проходят через оптический центр либо один из фокусов линзы, и лучи, параллельно расположенные главной либо одной из побочных оптических осей. Рисунки 3 . 3 . 3 и 3 . 3 . 4 демонстрируют данные построения.
Рисунок 3 . 3 . 3 . Построение изображения в собирающей линзе.
Рисунок 3 . 3 . 4 . Построение изображения в рассеивающей линзе.
Стоит выделить то, что стандартные лучи, использованные на рисунках 3 . 3 . 3 и 3 . 3 . 4 для построения изображений, не проходят через линзу. Данные лучи не используются в построении изображения, но могут быть использованы в этом процессе.
Для расчета положения изображения и его характера используется формула тонкой линзы. Если записать расстояние от предмета до линзы как d , а от линзы до изображения как f , то формула тонкой линзы имеет вид:
1 d + 1 f + 1 F = D.
Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию.
Диоптрия ( д п т р ) является единицей измерения оптической силы, фокусное расстояние которой равно 1 м : 1 д п т р = м — 1 .
Формула тонкой линзы аналогична формуле сферического зеркала. Можно вывести ее для параксиальных лучей из подобия треугольников на рисунках 3 . 3 . 3 либо 3 . 3 . 4 .
Фокусное расстояние линз записывается с определенными знаками: собирающая линза F > 0 , рассеивающая F 0 .
Величина d и f тоже подчиняются определенным знакам:
- d > 0 и f > 0 – применительно к действительным предметам (то есть реальным источникам света) и изображений;
- d 0 и f 0 – применительно к мнимым источникам и изображениям.
Для случая на рисунке 3 . 3 . 3 F > 0 (линза собирающая), d = 3 F > 0 (действительный предмет).
Из формулы тонкой линзы получаем: f = 3 2 F > 0 , означает, что изображение действительное.
Для случая на рисунке 3 . 3 . 4 F 0 (линза рассеивающая), d = 2 | F | > 0 (действительный предмет), справедлива формула f = — 2 3 F 0 , следовательно, изображение мнимое.
Линейные размеры изображения зависят от положения предмета по отношению к линзе.
Линейное увеличение линзы Г – это отношение линейных размеров изображения h ‘ и предмета h .
Величину h ‘ удобно записывать со знаками плюс или минус, в зависимости от того, прямое оно или перевернутое. Она всегда положительна. Потому для прямых изображений применяется условие Γ > 0 , для перевернутых Γ 0 . Из подобия треугольников на рисунках 3 . 3 . 3 и 3 . 3 . 4 нетрудно вывести формулу для расчета линейного увеличения тонкой линзы:
В примере с собирающей линзой на рисунке 3 . 3 . 3 при d = 3 F > 0 , f = 3 2 F > 0 .
Значит, Г = — 1 2 0 – изображение перевернутое и уменьшенное в два раза.
В примере с рассеивающей линзой на рисунке 3 . 3 . 4 при d = 2 | F | > 0 , справедлива формула f = — 2 3 F 0 ; значит, Г = 1 3 > 0 – изображение прямое и уменьшенное в три раза.
Оптическая сила D линзы находится в зависимости от радиусов кривизны R 1 и R 2 , ее сферических поверхностей, а также и от показателя преломления n материала линзы. В теории оптики имеет место следующее выражение:
D = 1 F = ( n — 1 ) 1 R 1 + 1 R 2 .
Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.
Многие оптические приборы устроены таким образом, что свет последовательно проходит через 2 или несколько линз. Изображение предмета от 1 -й линзы служит предметом (действительным или мнимым) для 2 -й линзы, выстраивающей, в свою очередь, 2 -е изображение предмета, которое также может быть действительным либо мнимым. Расчет оптической системы из 2 -х тонких линз состоит в
2 -кратном применении формулы линзы, причем расстояние d 2 от 1 -го изображения до 2 -й линзы следует предложить равное величине l – f 1 , где l – это расстояние между линзами.
Вычисленная, по формуле линзы, величина f 2 предопределяет положение 2 -го изображения, а также его характер ( f 2 > 0 – действительное изображение, f 2 0 – мнимое). Общее линейное увеличение Γ системы из 2 -х линз равняется произведению линейных увеличений 2 -х линз, то есть Γ = Γ 1 · Γ 2 . Если предмет либо его изображение находятся в бесконечности, тогда линейное увеличение не имеет смысла.
Видео:7.6 Формула тонкой линзыСкачать

Астрономическая труба Кеплера и земная труба Галилея
Рассмотрим частный случай – телескопический ход лучей в системе из 2 -х линз, когда и предмет, и 2 -е изображение расположены на бесконечно больших расстояниях друг от друга. Телескопический ход лучей выполняется в зрительных трубах: земной трубе Галилея и астрономической трубе Кеплера.
Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.
Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.
Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто.
Смысл хроматической аберрации в том, что на показатель преломления материала линзы влияет длина световой волны λ . Данное свойство прозрачных сред называют дисперсией. Фокусное расстояние линзы различно для света с различными длинами волн. Данный факт приводит к размытию изображения при излучении немонохроматического света.
Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.
В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.
Видео:10 км классика. Лента Optiwax, руки на расслабоне.Скачать

Что представляет собой фотоаппарат
Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.
Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер d данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия a F , как показано на рисунке 3 . 3 . 5 . Это в результате увеличивает глубину резкости.
Рисунок 3 . 3 . 5 . Фотоаппарат.
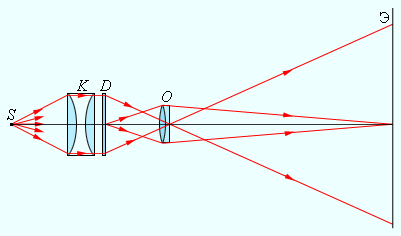
С помощью проекционного аппарата удается снять масштабные изображения. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D ) на удаленном экране Э (рисунок 3 . 3 . 6 ). Система линз K (конденсор) используется для концентрации света источника S на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом D и объективом O .
Рисунок 3 . 3 . 6 . Проекционный аппарат.
Рисунок 3 . 3 . 7 . Модель тонкой линзы.
Рисунок 3 . 3 . 8 . Модель системы из двух линз.
Видео:Урок 212 (осн). Формула тонкой линзыСкачать

Формула тонкой линзы
теория по физике 🧲 оптика
Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.
- расстояние от предмета до линзы — d (м);
- расстояние от изображения до линзы— f (м);
- фокусное расстояние линзы — F (м).
Видео:Урок 398. Задачи на формулу тонкой линзы - 1Скачать

Вывод формулы
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
B O O B 1 . . = A B A 1 B 1 . .
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
C O A 1 B 1 . . = O F F B 1 . .
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
A B A 1 B 1 . . = C O A 1 B 1 . .
Отсюда следует, что:
B O O B 1 . . = O F F B 1 . .
B O является расстоянием от предмета до линзы. Обозначим его за d. O B 1 является расстоянием от линзы до изображения. Обозначим его за f. O F является фокусным расстоянием линзы. Обозначим его за F. F B 1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
Избавимся от знаменателей и получим:
Или можно записать так:
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Формула тонкой линзы
1 d . . + 1 f . . = 1 F . .
Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:
1 d . . + 1 f . . = D
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Правила расстановки знаков перед членами уравнения в формуле линзы
- Если линза собирающая, то ее фокус действительный, и перед членом 1 F . . ставят знак «плюс» ( 1 F . . ) .
- Если линза рассеивающая, то ее фокус мнимый, и перед членом 1 F . . ставят знак «минус» ( − 1 F . . ) .
- Если изображение действительное, то перед величиной 1 d . . ставят знак «плюс» ( 1 d . . ) .
- Если изображение мнимое, то перед величиной 1 d . . ставят знак «минус» ( − 1 d . . ) .
- Величина 1 f . . всегда имеет знак «плюс», поскольку расстояние от предмета до линзы всегда положительное.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
1 d . . + 1 f . . = 1 F . .
1 d . . + 1 15 . . = 1 10 . .
Умножим выражение на 150d:
150 + 10 d = 15 d
Видео:Урок 211 (осн). Задачи на построение изображений с помощью линзСкачать

Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
Линейное увеличение — отношение линейного размера изображения к линейному размеру предмета. Линейное увеличение обозначают буквой Γ .
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
Сначала применим формулы тонкой линзы:
1 d . . + 1 f . . = 1 F . .
Она необходима, чтобы выразить фокусное расстояние линзы:
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Отсюда это расстояние равно:
Подставим полученное выражение в формулу фокусного расстояния линзы:
F = f h H . . f f h H . . + f . . = f 2 h H . · H f h + f H . . = f h H + h . .
F = f h H + h . . = 4 · 0 , 02 1 + 0 , 02 . . ≈ 0 , 08 ( м ) = 8 ( с м )

📽️ Видео
Формула тонкой линзыСкачать

Урок 396. Построение изображений с помощью линзСкачать