Уравнение термодинамики в открытой системе

Внутренняя энергия – не единственный вид энергии, которым может обладать термодинамическая система. Рассмотрим небольшой объем жидкости, движущейся вместе с окружающим ее потоком. Такая жидкая частица обладает кинетической энергией, потенциальной энергией в поле сил тяжести и, наконец, внутренней энергией. Сумма этих трех энергий есть полная энергия системы. Из сказанного ясно, что к внутренней энергии относится та часть полной энергии термодинамической системы, которая не связана с движением системы как целого и с положением системы в поле сил тяжести.

В этой связи открытые системы имеют ряд особенностей, отличающих их от закрытых систем.

1. В общем балансе энергии дополнительно к изменению внутренней энергии необходимо учитывать изменение кинетической энергии, которой обладает рабочее тело, двигающееся относительно границ системы.

2. При вводе рабочего тела необходимо преодолевать действие внутреннего давления в системе, то есть совершать работу проталкивания.

3. Рабочее тело, находясь в пределах системы, может производить работу, не связанную с деформацией системы, то есть с изменением ее объема. Это работа, например, совершаемая газом при вращении ротора турбины. Работа рабочего тела в проточной системе, не связанная с деформацией границ, называется технической работой L_т.

4. В некоторых случаях может играть существенную роль изменение потенциальной энергии рабочего тела в поле внешних сил.

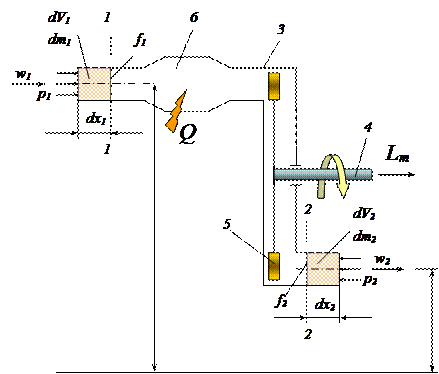
Для учета особенностей открытых термодинамических систем в уравнении первого закона термодинамики рассмотрим схему такой системы (рис. 2.7). Границы системы образованы сечением 1-1 (вход рабочего тела в систему), сечением 2-2 (выход рабочего тела), жесткими стенками 3 и сечением 4 вращающегося вала. Вал передает в окружающую среду (потребителю) техническую работу L_т, совершаемую в системе при взаимодействии потока рабочего тела с лопатками 5 ротора турбины. Рабочее тело может получать некоторое количество теплоты Q, например, за счет сжигания топлива в камере сгорания 6. Потенциальная энергия рабочего тела при его движении изменяется, так как центры тяжести входного и выходного сечений расположены на разной высоте.

Рис. 2.7. Схема открытой термодинамической системы.

Изменение энергии системы за малый промежуток времени dt составит:

где dE – изменение полной энергии системы;

dE_п – количество энергии, поступающей в систему из окружающей среды;

dЕ_р – количество энергии, отдаваемой системой в окружающую среду.

За рассматриваемый промежуток времени в систему через сечение 1-1 со скоростью w₁ входит рабочее тело массой dm₁, обладающее удельной внутренней энергией u₁, и вносит в систему: собственную внутреннюю энергию u₁dm₁, кинетическую энергию dm₁w₁ 2 /2, потенциальную энергию gz₁dm₁.

При вводе рабочего тела силы внешнего давления р₁ совершают над системой работу ввода dL_вв. Давление р₁, действуя на сечение площадью f₁, создает силу р₁f₁, точка приложения которой перемещается на расстояние dx₁, необходимое для того, чтобы элементарная масса dm₁ оказалась введенной в систему через сечение 1-1. Таким образом, работа ввода равна:

Кроме того, находясь в системе, рабочее тело за время dt получит количество теплоты dQ.

В итоге количество энергии, поступающей в систему, выразится суммой:

Аналогично определяется и расход энергии, но с некоторыми отличиями:

— во-первых, будет совершаться не работа ввода, а работа вывода р₂dV₂;

— во-вторых, место подведенной теплоты займет отводимая техническая работа;

— в-третьих, одновременно с совершением технической работы dL_т, может совершаться работа расширения dL = рdV, связанная со смещением границ системы.

Тогда изменение полной энергии системы будет равно:

Если осуществляется стационарный процесс, то поступление массы рабочего тела и энергии в систему равно их расходу, а объем системы постоянен.

При этих условиях деление всех членов уравнения на dm дает удельные величины, отнесенные к 1 кг рабочего тела, прошедшего через систему:

Перепишем это уравнение иначе:

Сумма внутренней энергии и произведения давления на объем рабочего тела, называется энтальпией h:

Так как эта сумма выражена через параметры состояния, то энтальпия также является функцией состояния. Физический смысл энтальпии рассматривается при анализе конкретных явлений.

Тогда, уравнение первого закона термодинамики для конечного изменения состояния рабочего тела в проточной термодинамической системе (интегральная форма) можно представить в виде:

где Dh = h₂ – h₁ – изменение удельной энтальпии рабочего тела (РТ);

D(w 2 /2) = w₂ 2 /2 – w₁ 2 /2 – изменение удельной кинетической энергии РТ;

D(gz) = gz₂ – gz₁ – изменение удельной потенциальной энергии РТ.

Для бесконечно малого изменения состояния РТ в элементарном процессе первый закон термодинамики в проточной термодинамической системе (дифференциальная форма) имеет вид:

Техническая работа l_т, изменение кинетической энергии D(w 2 /2) и изменение потенциальной энергии D(gz) представляют собой величины механической природы. В пределах термодинамической системы эти количества могут претерпевать взаимное преобразование. Так, например, техническая работа в турбине может совершаться за счет уменьшения кинетической энергии потока или уменьшения его потенциальной энергии (при падении с верхнего уровня на нижний). В связи с этим: сумма технической работы, изменения кинетической энергии и изменения потенциальной энергии называется располагаемой работой l_о:

Тогда уравнения первого закона термодинамики для стационарной проточной системы могут быть записаны в виде:

Для равновесных термодинамических процессов указанные выражения можно выразить через изменение параметров состояния рабочего тела в процессе. Но в начале установим, как рассчитывается располагаемая работа. Продифференцируем выражение энтальпии:

Изменение внутренней энергии заменим уравнением первого закона термодинамики для закрытых систем: du = dq – dl = dq – рdu. А дифференциал d(рu) представляет собой дифференциал сложной функции: d(рu) = рdu + udр. Тогда,

Заменив левую часть полученного выражения уравнением первого закона термодинамики для открытой системы, получим выражение для расчета располагаемой работы:

Следовательно, элементарная располагаемая работа определяется произведением объема на изменение давления, взятым с обратным знаком.

В конечном процессе располагаемая работа находится интегрированием от начального 1 до конечного 2 состояния рабочего тела в процессе:

.

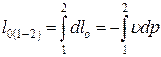
Таким образом, уравнения первого закона термодинамики для проточной системы могут быть записаны так:

Dh = q – l_о Þ .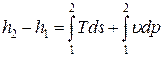

Тема: «ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ»(2 часа)

1. Общие положения второго закона термодинамика.

2. Прямой термодинамический цикл.

3. Обратный термодинамический цикл.

4. Формулировки второго закона термодинамики.

Основная литература

1. Амерханов Р.А., Драганов Б.Х. Теплотехника. — М.: Энергоатомиздат, 2006. – 432 с.

Дополнительная литература

1. Теплотехника. /А.П. Баскаков, Б.В. Берг и др. – М.: Энергатомиздат, 1991. – 224 с.

2. Техническая термодинамика. / Кириллин В.А., Сычев В.В., Шейндлин А.Е. – М.: Издательский дом МЭИ, 2008. – 496 с.

Общие положения второго закона термодинамика

Первый закон термодинамики, закон сохранения и превращения энергии, дают количественную характеристику превращения энергии. Однако первый закон термодинамики не указывает направления процессов и не имеет в этом отношении ограничений. Так, первый закон термодинамики не делает различий между преобразованием работы в теплоту (l ® q) и теплоты в работу (q ® l). Хотя количественные соотношения при том и другом преобразовании одинаковы, между этими преобразованиями имеется существенное различие. Превращение работы в теплоту – положительное превращение энергии, идущее естественным путем. Превращение теплоты в работу – отрицательное превращение энергии, которое осуществляется при особых условиях. Вот об этих условиях и говорит второй закон термодинамики.

Прежде чем непосредственно перейти ко второму закону термодинамики остановимся на понятиях об обратимых и необратимых процессах.

Обратимыми называются процессы, в результате совершения которых в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние. Следовательно, совокупность прямого и обратного процессов не вызывает в окружающей среде никаких изменений.

В случае обратимых процессов обратный процесс представляет собой, так называемое «зеркальное отображение» прямого процесса. Если, например, в прямом процессе к системе подводится какое-то количество теплоты, то в обратном процессе от системы отводится точно такое же количество теплоты. Если в прямом процессе система совершает работу над окружающей средой, то в обратном процессе окружающая среда производит над системой работу, равную по абсолютной величине работе в прямом процессе.

Необратимыми называются процессы, при проведении которых в прямом и затем в обратном направлении система не возвращается в исходное состояние. Из повседневной практики известно, что все естественные самопроизвольные процессы, происходящие в природе, являются необратимыми. Обратимых процессов в природе не существует.

Кроме того, опыт показывает, что реальные процессы имеют определенную направленность передачи энергии. Так известно, что непосредственная самопроизвольная передача энергии между двумя системами в виде работы происходит только тогда, когда давление в системах разное. И энергия передается от системы с большим давлением к системе с меньшим давлением и никогда наоборот. Аналогичная картина наблюдается и при передаче энергии в форме теплоты: теплота сама собой переходит только от тела с большей температурой к телу с меньшей температурой. Процессы эти являются неравновесными и тем больше, чем больше разность давлений или соответственно температур между взаимодействующими телами.

Таким образом, при непосредственном взаимодействии между телами с разными давлениями и температурами энергия передается только необратимо и обязательно в направлении меньшего давления (передача энергии в форме работы) и меньшей температуры (передача энергии в форме теплоты).

Вместе с тем, самопроизвольные процессы окружающей нас действительности идут в направлении перехода системы от менее вероятных состояний к состояниям более вероятным. Наиболее вероятным состоянием является такое, при котором изолированная система находится в полном равновесии. Полное равновесие означает отсутствие условий для протекания какого-либо процесса в системе. Отсутствие разности давлений, температур, т.е. все интенсивные свойства такой системы выравнены.

Можно утверждать и обратное, если в изолированной системе протекают процессы, приводящие систему от менее вероятных состояний к более вероятным, то такие процессы являются естественными, необратимыми.

В рассмотренных положениях заключается наиболее общая сущность второго закона термодинамики:

1. Не все процессы, не противоречащие первому закону термодинамики, протекают в действительности самопроизвольно с положительным превращением энергии. Есть процессы с отрицательным превращением энергии (q ® l), которые самопроизвольно идти не могут.

2. Все реальные процессы протекают в определенном направлении, задаваемом условиями равновесия. Все они идут в одном направлении – направлении достижения равновесия системы, как наиболее вероятного состояния.

3. Процессы идут до установления равновесия системы, т.е. до момента выравнивания интенсивных свойств системы (температуры, давлений).

Видео:Термодинамические системы, параметры. Равновесное, неравновесное состояния терм. систем. 10 класс.Скачать

Термодинамика открытых систем

Вы будете перенаправлены на Автор24

В термодинамике под открытой понимается такая термодинамическая система, которая обладает способностью к обмену с окружающей средой массой, работой и теплотой. Системами открытого типа считаются живые системы, которые также называют неравновесными.

Живой организм может получать пищу, воду и кислород из внешней среды, при этом он выделяет в нее разные вещества. Теплообмен осуществляется между средой и организмом.

Видео:Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Открытые системы

Рисунок 1. Термодинамика для открытых систем. Автор24 — интернет-биржа студенческих работ

Открытые системы способны производить непосредственный энергообмен с окружающей средой посредством вещества, информации и импульса. Все реальные системы будут считаться при этом открытыми. К самому значимому типу открытых систем относятся химические, в пределах которых осуществляются определенные реакции.

Живые организмы и экосистемы также можно рассматривать как открытые химические системы. Такой подход позволяет проводить важные исследования процессов их жизнедеятельности и активного развития на платформе законов неравновесной термодинамики, физической и химической кинетики. Открытые системы в условиях неорганической природы осуществляют определенный обмен с внешней средой, состоящей из разных систем. Этим системам свойственны вещество и энергия.

Неравновесное состояние в этом случае будет характеризоваться параметрами, аналогичными равновесным:

• определенной температурой;
• химическим потенциалом компонентов системы.

Энтропия в открытых системах также сохранит свою неизменность. Это объясняется тем, что в них осуществляются необратимые процессы, но при этом энтропия накапливаться не будет. Она выводится в окружающую среду.

Готовые работы на аналогичную тему

Видео:ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать

Свойства открытых систем в термодинамике

В открытых системах наиболее уникальные свойства будут проявляться в условиях нелинейных процессов (когда в них мы наблюдаем вероятность появления термодинамических, устойчивых неравновесных состояний). При этом их характеризует определенная временная (пространственная) упорядоченность. Это диссипативная структура, само существование которой подразумевает наличие факта непрерывного обмена окружающей среды с веществом (энергией).

Автором первого определения открытой системы стал австрийский физик Э. Шредингер. Он сделал акцент на особенности биологических систем, которая должна заключаться в непосредственном энерго-вещественном обмене с окружающей средой. Система, взаимодействующая со средой, не способна сохранять свою замкнутость. Это объясняется тем, что она должна получать новые вещества или энергию. При этом данная система должна одновременно выводить в пространство отработанную энергию (использованное вещество).

При поступлении энергии (или вещества) неравновесность в системе растет. Следствием этого становится процесс разрушения прежних связей элементов системы друг с другом, которые определяют ее структуру. В такой ситуации возникают новые связи между элементами, они способствуют кооперативным процессам.

В качестве примера наглядной демонстрации процессов самоорганизации можно рассмотреть работу лазера. Хаотические колебательные движения, которые совершают частицы кристалла, будут приводиться в движение за счет энергии, поступающей извне. Это провоцирует повышение мощности лазерного излучения. Г. Хакен, исследуя процессы самоорганизации в лазере, охарактеризовал новое направление исследований – синергетическое.

В качестве еще одного примера можно рассматривать самоорганизацию в химических реакциях. Она связана с поступлением извне новых реагентов – веществ. Эти вещества отвечают за обеспечение продолжения реакции и за выведение в окружающую среду ее продуктов.

В формате открытых систем нелинейные процессы изучаются на базе уравнений химической кинетики. Накапливающиеся в открытых системах активные продукты реакции (теплоты) могут спровоцировать автоколебательный режим реакций. Для этого будет нужна реализация в системе обратной связи. Это, в свою очередь, характеризуется ускорением реакции под воздействием или продукта, или теплоты, выделяющейся при реакции.

Что касается открытой химической системы, то в ней (с наличием положительной обратной связи) возникают саморегулирующиеся непрекращающиеся химические реакции. Внешне самоорганизация проявляется с возникновением концентрических волн в жидкой среде. Это особенно заметно в автоколебательных реакциях, открытых Б. Белоусовым.

На основании проводимых Р. Пригожиным экспериментов с периодическими реакциями, ему удалось построить брюсселятор (теоретическую модель, положенную впоследствии в основу нелинейной или неравновесной термодинамики).

Рисунок 2. Энтропия в открытых системах. Автор24 — интернет-биржа студенческих работ

Нелинейность в термодинамике означает задействование в ней нелинейных математических уравнений, где содержатся переменные во второй или выше степени. Открытие самоорганизации системы в условиях простейшей неорганической природы играет существенную роль в научном и мировоззренческом понимании. Это демонстрирует вероятность осуществления процессов в основе материи и рассматривает взаимосвязь органической и неорганической природы.

С позиции самоорганизации весь окружающий мир и Вселенная будут представлять собой комплекс разносторонних и самоорганизующихся процессов, выступающих основанием для любой эволюции.

Видео:Первый закон термодинамики. 10 класс.Скачать

Энтропия открытых систем в термодинамических процессах

При неравновесном состоянии энтропия открытых систем определяется суммой значений энтропий отдельных малых элементов в системе. Эти элементы пребывают в состоянии локального равновесия (следствие аддитивности энтропии).

Потоки энергии и вещества в системе провоцируются процессом отклонений параметров термодинамики от их равновесных значений. Повышение энтропии системы становится возможным за счет процессов переноса. Энтропия в рамках замкнутых систем будет расти и при этом стремиться к своему максимуму и равновесному значению.

В открытой системе допускается вероятность стационарных состояний с постоянной энтропией (при условии ее постоянного производства). При этом энтропия должна быть отведена от системы. В термодинамике открытых систем стационарному состоянию отводится роль, аналогичная термодинамическому равновесию (термодинамика равновесных процессов в отношении изолированных систем).

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Первый закон термодинамики

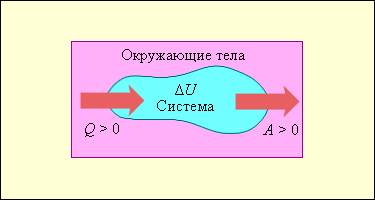
На рисунке 3 . 9 . 1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q > 0 , если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A > 0 .

Рисунок 3 . 9 . 1 . Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы Δ U .

Видео:ФИЗИКА ЗА 5 МИНУТ - ТЕРМОДИНАМИКАСкачать

Определение 1 -го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Видео:Законы Термодинамики. Что Такое Термодинамика?Скачать

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В изохорном процессе, то есть в условиях неизменного объема ( V = c o n s t ) , газ не совершает работы, A = 0 .

В этом случае справедливой будет формула внутренней энергии газа:

Q = ∆ U = U ( T 2 ) — U ( T 1 ) .

В данном выражении U ( T 1 ) и U ( T 2 ) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло ( Q > 0 ) , чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам ( Q 0 ) .

В изобарном процессе, предполагающем постоянность значения давления ( p = c o n s t ) , работа, совершаемая газом, выражается в виде соотношения:

A = p ( V 2 — V 1 ) = p ∆ V .

Первый закон термодинамики для изобарного процесса дает:

Q = U ( T 2 ) — U ( T 1 ) + p ( V 2 — V 1 ) = ∆ U + p ∆ V .

При изобарном расширении Q > 0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q 0 тепло переходит внешним телам. В таком случае A 0 . При изобарном сжатии уменьшаются температура газа T 2 T 1 и значение внутренней энергии Δ U 0 .

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0 .

Первый закон термодинамики для изотермического процесса выражается соотношением

Теплота Q , приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

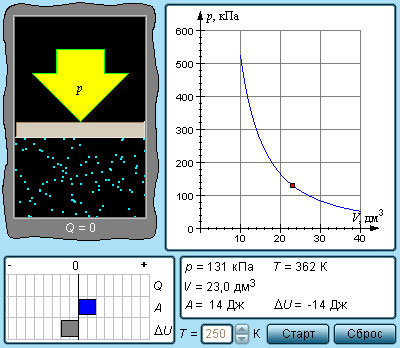
Рисунок 3 . 9 . 2 . Модель адиабатического процесса.

В адиабатическом процессе Q = 0 . По данной причине первый закон термодинамики принимает вид:

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Расширение или сжатие газа на плоскости p , V проиллюстрирована кривой, называемой адиабатой.

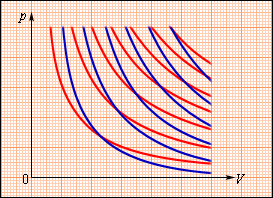
В процессе адиабатического расширения газом совершается положительная работа A > 0 , что является причиной понижения значения внутренней энергии Δ U 0 . Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3 . 9 . 3 ).

Рисунок 3 . 9 . 3 . Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат ( p , V ) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид:

p V γ = c o n s t .

Данное выражение, в котором γ = C p C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ = 5 3 = 1 , 67 , двухатомного γ = 7 5 = 1 , 4 , многоатомного γ = 1 , 33 .

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

A = C V ( T 2 — T 1 )

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу Δ Q T . Так как на каждом участке адиабатического процесса Δ Q = 0 , энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

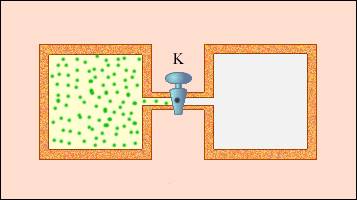
Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3 . 9 . 3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q = 0 , по той причине, что исключен теплообмен с окружающими телами, и A = 0 , так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что Δ U = 0 , то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости ( p , V ) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Рисунок 3 . 9 . 4 . Расширение газа в пустоту.

🔥 Видео

Основы химической термодинамикиСкачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Энтропия и второй закон термодинамики (видео 6) | Энергия| БиологияСкачать

Что такое Энтропия?Скачать

Термодинамика | уравнение состояния термодинамической системыСкачать

Урок 171. Простейшие задачи на 1-й закон термодинамикиСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Первый закон термодинамикиСкачать

Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать

Коробов М. В. - Физическая химия. Часть 1 - Теплота и работа. Первый закон термодинамикиСкачать