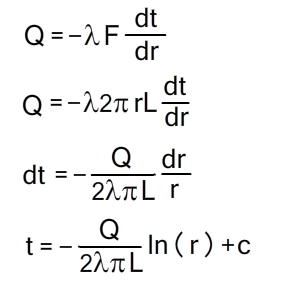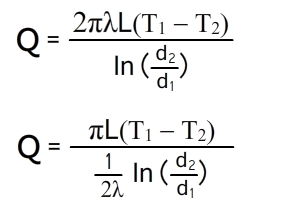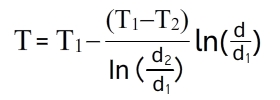Уравнение термическое сопротивление для плоской стенки (4 видео)

Теплопроводность через стенку

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.

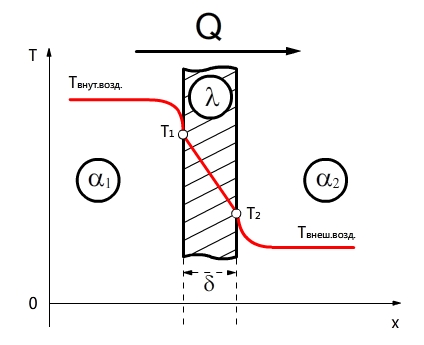
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.

Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).

Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.

Теплопередача через непроницаемую стенку включает в себя следующие процессы:

теплоотдачу от горячей среды к стенке;
теплопроводность внутри стенки;
теплоотдачу от стенки к холодной среде.

Содержание

Теплопередача через плоскую стенку (граничные условия первого рода)
Распределение температуры в плоской стенке
Теплопроводность через многослойную стенку
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Тема 12.Теплопередача
12.1. Теплопередача через плоскую стенку
Лекция 13. Теплопроводность при стационарном режиме. Плоская стенка. Термическое сопротивление. Коэффициент теплопередачи.
💥 Видео

Видео:Видео лекция.Теплопроводность через плоскую стенкуСкачать

Теплопередача через плоскую стенку (граничные условия первого рода)

Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.

Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.

Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).

Поверхностная плотность теплового потока рассчитывается по формуле:

где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].

На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:

где δ = dx — толщина стенки, λ

λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.

а обратная величина —

R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.

Для теплового потока формулу так же можно представить в виде:

Общее количество теплоты проходящее через площадь стены S за время t можно представить как:

Видео:Теплопередача через плоскую стенкуСкачать

Распределение температуры в плоской стенке

Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C₁; T=C₁х+С₂ (1). Определим С₁ и С₂ через граничные условия.

При х=0 T=T₁, подставим в уравнение (1) и получим T₁=С₂.
При х=δ T=T₂, подставим в уравнение (1) и получим T₂=С₁*δ+С₂, T₂=С₁*δ+T₁, получим: С₁=(Т₂-T₁)/δ. Теперь подставим в уравнение (1) найденные С₁ и С₂, получим следующее распределение температуры в нашей стене:

Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:

Видео:Теплопроводность плоской стенкиСкачать

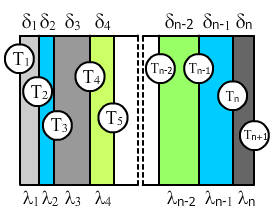
Теплопроводность через многослойную стенку

Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λ_i и разной толщиной δ_i.

Термическое сопротивление стенки считается так:

Для теплового потока формула будет иметь вид:

Температура на границе слоя вычисляется по следующей формуле:

Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:

Эквивалентная теплопроводность многослойной стенки:

Видео:Теплотехнический расчет стеныСкачать

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

q = k * (T_{возд.внутри} — T_{возд.снаружи}); Вт/м 2

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

Видео:Передача тепла теплопроводностьюСкачать

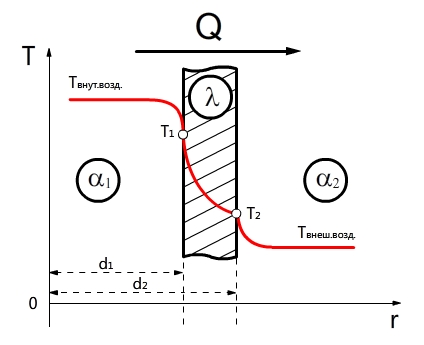
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Видео:Тепловая задача - Многослойная плоская стенкаСкачать

Тема 12.Теплопередача

Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

12.1. Теплопередача через плоскую стенку

Теплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители.

Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена.

При передаче теплоты от стенки к окружающей среде в основном преобладает конвективный теплообмен, поэтому будут рассматриваться такие задачи.

1). Теплопередача через плоскую стенку.

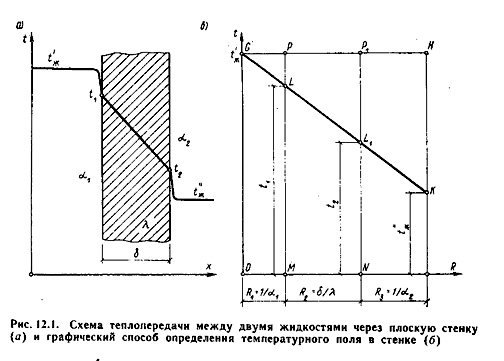
Рассмотрим однослойную плоскую стенку толщиной d и теплопроводностью l (рис12.1).

Температура горячей жидкости (среды) t ‘ _ж, холодной жидкости (среды) t » _ж.

Количество теплоты, переданной от горячей жидкости (среды) к стенке по закону Ньютона-Рихмана имеет вид:

где a ₁ – коэффициент теплоотдачи от горячей среды с температурой t ‘ _ж к поверхности стенки• с температурой t₁;

F – расчетная поверхность плоской стенки.

Тепловой поток, переданный через стенку определяется по уравнению:

Тепловой поток от второй поверхности стенки к холодной среде определяется по формуле:

где a ₂ – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t » _ж.

Решая эти три уравнения получаем:

где К = 1 / (1/ a ₁ + / l + 1/ a ₂) – коэффициент теплопередачи, (12.5)

R₀ = 1/К = (1/ a ₁ + d / l + 1/ a ₂) – полное термическое сопротивление теплопередачи через однослойную плоскую стенку. (12.6)

1/ a ₁, 1/ a ₂ – термические сопротивления теплоотдачи поверхностей стенки;

d / l — термическое сопротивление стенки.

Для многослойной плоской стенки полное термическое сопротивление будет определяться по следующей формуле:

Видео:Теплоотдача и теплопередача.Скачать

Лекция 13. Теплопроводность при стационарном режиме. Плоская стенка. Термическое сопротивление. Коэффициент теплопередачи.

Теплопроводность —один из видов переноса теплоты (энергии теплового движения микрочастиц) от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры. При Т. перенос энергии в теле осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией.

Стационарный режим— режим функционирования системы, который устанавливается с течением времени, в дальнейшем его характеристики остаются неизменными.

Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным: t = f(x,y,z) , ∂t/∂i= 0

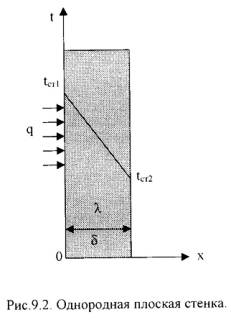
1).Однородная плоская стенка (Рис.13.1)

Рис.13.1 Однородная плоская стенка

Температуры поверхностей стенки –t_ст1 и t_ст2.Плотность теплового потока:

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м 2 ∙К)/Вт], то плотность теплового потока:

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Температура тела в точке с координатой х находится по формуле:

2).Многослойная плоская стенка.

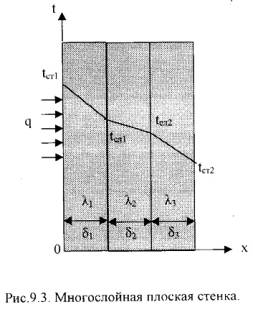
Рассмотрим 3-х слойную стенку (Рис.13.2). Температура наружных поверхностей стенокt_ст1и t_ст2, коэффициенты теплопроводностислоевλ₁, λ₂, λ₃, толщина слоевδ₁, δ₂, δ₃.

Рис.13.2 Многослойная плоская стенка

Плотности тепловых потоков через каждый слой стенки:

Решая эти уравнения, относительно разности температур и складывая, получаем:

где: R_o= (δ₁/λ₁+ δ₂/λ₂ + δ₃/λ₃) – общее термическое сопротивление теплопроводности многослойной стенки. Температура слоев определяется по следующим формулам: