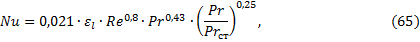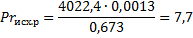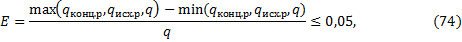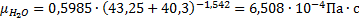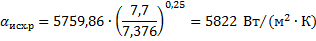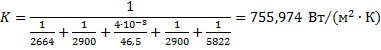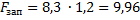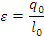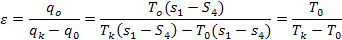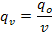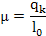Уравнение теплового баланса холодильной установки (8 видео)

Тепловой баланс холодильника

Количество теплоты, которое необходимо отвести от раствора для его охлаждения:

G_кон — расход упаренного раствора, (кг/с);

с_кон — удельная теплоёмкость упаренного раствора при t_ср и x_кон,(Дж/кг·К);

с_в — удельная теплоёмкость воды, (Дж/кг·К).

Зададим начальную температуру воды:

Конечная температура раствора:

Принимаем t_к.в.из интервала 25– 30 (°С):

Рассчитаем среднюю разность температур ∆t_ср:

Dt_ср = (34)

Dt_ср = = 29,31( ̊С).

Среднюю температуру t_в найдём как среднее арифметическое:

t_в =

t_в = = 20(°С)

Средняя температура упаренного раствора t_cp_.конц._p:

Для этого рассчитаем теплоёмкость воды при t_cp_.конц._p:(Приложение А,3)

с₀ = 4223,6 + 2,476·49,31·log(49,31/100) = 4,186·10 3 Дж/(кг·К);

c_кон=4186+(-5297,21+6942,68·0,1+14,84·49,31-14,15·10 -3 ·49,31 2 )·0,1

Тогда по формуле (31) количество теплоты равно:

Q = 0,38·3,795·10 3 ·(80,7-25) =0,8·10 5 (Вт)

Найдем расход воды по формуле:

Рассчитаем с_в(Приложение А,3):

с_в = 4223,6 + 2,476·20·log(20 /100) = 4,188·10 3 ( Дж/(кг·К));

G_в = 0,8·10 5 /4,188·10 3 ·(30-10)=0,95 (кг/с)

Ориентировочный расчёт и выбор холодильника

Зададим ориентировочный коэффициентом теплопередачи от жидкости к жидкости [2], c.172:

Рассчитаем ориентировочную площадь теплообмена по формуле (30) :

F = 0,8·10 5 / ( 1250·23,78) = 2,6(м 2 )

С учётом запаса :

F = 1.1 ·2,6= 2,86(м 2 )

Рассчитаем скорость течения раствора w_трпо трубному пространству холодильника с диаметром труб d = 25×2 мм и площадь сечения трубного пространства, необходимая для обеспечения необходимого режима течения.

Re = = 10000 (36)

r_кон — плотность раствора при температуре t_cp_.конц._p и x_кон, (кг/м 3 );

d_э – эквивалентный диаметр, (м);

w_тр –скорость течения раствора в трубном пространстве, (м/с).

m_в = 0.59849·(43.252 +49,31) -1.5423 = 5,54·10 -4 (Па·с)

m_кон=

Найдём r_кон – плотность раствора при t_cp_.конц._pи x_кон(Приложение А.1) :

r_в = 1000 – 0,062· – 0,00355· 2 = 989,53(кг/м 3 )

r_кон=

Примем эквивалентный диаметр равным d_э = 0,021 м

Скорость течения раствора в аппарате вычисляется по формуле:

W_тр= 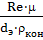(37)

W_тр= = 0,1(м/с)

Площадь проходного сечения трубного пространства s_трвычисляется по формуле:

s_тр = (38)

s_тр = = 3,4·10 -3 (м 2 )

Наименьший кожухотрубчатый холодильник диаметра 159(мм) имеет s_тр = 0,5 ·10 -2 (м 2 ).

Следовательно, для обеспечения турбулентного режима течения раствора необходим аппарат с меньшим сечением трубного пространства, т.е. теплообменник «труба в трубе».

Выбор аппарата:

Эквивалентный диаметр трубного пространства

Исходя из расчётных данных , проходное сечение трубного пространства s_трстандартного аппарата может быть принято для расчётов :

Тогда , скорость течения раствора в трубном пространстве может быть вычислена по формуле:

w_тр = (39)

w_тр = = 0,277(м/с)

Эквивалентный диаметр межтрубного пространства

d_э = 0,108–0,01 – 0,048 = 0,05(м)

Исходя из расчётных данных, проходное сечение межтрубного пространства s_меж_трстандартного аппарата может быть принято для расчётов:

Тогда , скорость течения раствора в межтрубном пространстве может быть вычислена по формуле:

w_межтр = (40)

w_межтр= = 0,152( м/с)

Значение Re_трвычислим по формуле (36):

Re_тр = = 51548

Значение Re_межтр вычислим по формуле :

Re_межтр = (41)

Re_межтр = = 35811

После ориентировочного расчёта холодильника исходя из площади теплообмена , площади проходных сечений и значений критерия Рейнольдса , мы должны сделать вывод о правильности выбора теплообменника. Проанализировав данные расчёта , делаем вывод , что для обеспечения требуемых параметров подходит следующий теплообменный аппарат , выбранный по каталогу :

Таблица 2 – Параметры холодильной установки (теплообменник «труба в трубе»)

Диаметр тубы , мм	Площадь проходного сечения , S·10 -4 , м 2	Поверхность теплообмена
Теплообменной	Кожуховой	Внутри теплообменной трубы	В кольцевом пространстве	Длина теплообменной трубы L = 6 м
48 х 4	108 х 5	12,6	57,3	0,890

Расчёт количества элементов

Определим число элементов n :

4.4.2 Подробный расчет холодильника

Коэффициенты теплоотдачи для конечного и исходного растворов определим из критериальной зависимости, полученной для теплоотдачи при развитом турбулентном течении в прямых трубах и каналах [6]:

где критерий Нуссельта, который можно рассчитать по следующей формуле:

По таблице 4.3 [6] значение поправочного коэффициента , учитывающего влияние на коэффициент теплоотдачи отношения длины трубы к ее диаметру ( ), принимаем равным единице.

критерий Прандтля, равный:

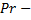
где параметры теплоносителя при его средней температуре.

критерий Прандтля, равный:

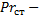
где параметры теплоносителя при температуре стенки.

Для того чтобы определить значение критерия Прандтля 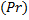для конечного и исходного растворов, необходимо рассчитать их теплопроводность при их средней температуре.

Теплопроводность конечного раствора при и рассчитывается по формулам (32) и (31):

Теплопроводность исходного раствора при и рассчитывается по формулам (32) и (31):

Зная параметры теплоносителей при их средних температурах вычислим критерий Прандтля (67):

Как и для ВА, задача определения коэффициентов теплоотдачи решается методом последовательных приближений. Для этого соотношение (65) приводят к виду:

где коэффициент, равный:

Для концентрированного раствора:

Для исходного раствора:

Для определения коэффициентов теплоотдачи методом последовательных приближений воспользуемся следующим алгоритмом:

1) Задать значение температуры стенки со стороны концентрированного раствора и значение температуры стенки со стороны исходного раствора .

2) Определить вязкость, теплопроводность и теплоемкость для концентрированного и исходного растворов при температурах стенок.

3) По формуле (67) рассчитать критерий Прандтля для концентрированного и исходного растворов , при температурах стенок.

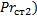
4) По формуле (69) определить коэффициенты теплоотдачи для концентрированного и исходного растворов 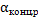и .

5) Определить коэффициент теплопередачи по следующей формуле:

где термическое сопротивление стенки со стороны концентрированного раствора, ;

термическое сопротивление стенки трубки, ;

термическое сопротивление стенки со стороны исходного раствора, ;

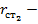
По таблице 31 [6] принимаем .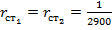

6) Найти поверхностные плотности тепловых потоков по формулам:

7) Определить расхождение плотностей тепловых потоков:

8) Если расхождение тепловых потоков более 5% необходимо определить температуры стенок по следующим уравнениям:

В первом приближении температуру стенки со стороны конечного раствора можно принять , со стороны исходного .

1) , .

2) Определим вязкость, теплопроводность и теплоемкость для концентрированного и при температуре стенки и :

Рассчитаем вязкость по формулам (35) и (34) :

Рассчитаем теплопроводность по формулам (32) и (31) :

Рассчитаем теплоемкость по формулам (19) и (18) :

Аналогично для исходно раствора при и :

3) Определим критерий Прандтля (67) при температурах стенок для концентрированного и исходного растворов:

4) По формуле (69) рассчитаем коэффициенты теплоотдачи для концентрированного и исходного растворов:

5) Зная коэффициенты теплоотдачи, по формуле (70) определим значение коэффициента теплопередачи:

6) Найдем поверхностную плотность теплового потока от концентрированного раствора к стенке (71):

Найдем поверхностную плотность теплового потока от стенки к исходному раствору (72):

Найдем поверхностную плотность теплового потока от концентрированного раствора к исходному раствору (73):

7) Определим расхождение плотностей тепловых потоков (74):

Расхождение тепловых потоков менее 5%, следовательно, требуемая точность достигнута, и расчет коэффициента теплопередачи окончен: .

По формуле (61) площадь поверхности теплообмена равна:

Поверхности теплопередачи принято принимать с запасом 20-30%, что дает следующее значение:

Определим количество элементов:

Проанализировав данные подробного расчета, можно сделать вывод, что выбранный ранее теплообменник типа «труба в трубе» удовлетворяет нашему расчету .

Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

Термодинамические основы холодильных машин

Принцип действия холодильной машин основан на втором законе термодинамики: для передачи теплоты ох холодного тела к теплому необходима затрата некоторой внешней работы.

Математически второй закон термодинамики выражается уравнением:

где|Q|— абсолютное значение теплоты, переданной теплому телу, Дж;

|Q₀| — абсолютное значение теплоты, отведенной от холодного тела, Дж;

|L| — внешняя работа, затраченная на передачу теплоты, Дж.

Машины, отбирающие теплоту от холодного тела и передающие ее нагретому, называются холодильными. Теплота от тела с низкой температурой переносится к телу с высокой температурой рабочим телом, циркулирующим в холодильной машине.

Холодильные машины, на работу которых затрачивается механическая энергия, относятся к компрессионным холодильным машинам, а в которых затрачивается тепловая энергия, к абсорбционным и пароэжекторным. В качестве рабочего тела могут быть использованы холодильные агенты и воздух. В первом случае холодильный эффект получают вследствие изменения агрегатного состояния рабочего тела – кипения жидкого холодильного агента при низких температурах. Холодильные машины, работающие с использованием холодильных агентов, называют паровыми. Во втором случае охлаждение достигается в результате перехода теплоты от охлаждаемой среды к холодному воздуху. Холодильные машины, работающие по этому принципу, являются воздушными. Преимущественно применяются паровые холодильные машины.

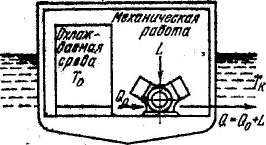
На рисунке 1.2 показан принцип работы холодильной машины. Рабочее тело отводит от холодного (охлаждаемой среды) теплоту Q₀ и передает ее нагретому, в качестве которого используют окружающий воздух или воду. По второму закону термодинамики для такого переноса следует затратить работу L.

Рисунок 1.2 — Принцип работы холодильной машины

Отдав нагретому телу теплоту Q = Q₀ + L, рабочее тело способно вновь отвести от холодного тела теплоту Qо, и процесс повторяется. Таким образом, рабочее тело в холодильной машине совершает круговой процесс или цикл. Цикл, на осуществление которого затрачивается работа, а результатом является перенос теплоты от холодного тела к теплому, называется обратным циклом. Холодильная машина работает по обратному циклу.

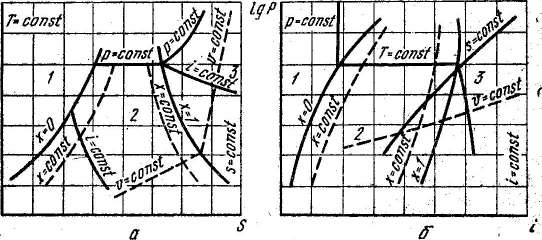
Тепловые диаграммы s — Т и i — lg р.Тепловые диаграммы служат для определения параметров рабочего тела при расчетах циклов холодильных машин. Наиболее распространенные диаграммы с осями: энтропия

В s—T-диаграмме (рисунок 1.3 (а)) на оси абсцисс откладывают энтропию, по оси ординат – абсолютную температуру, соответственно сетка диаграммы образована адиабатами 5=соп5т (вертикальные прямые) и изотермами Т=соп51: (горизонтальные прямые).

Рис. 1.3 – Принцип работы холодильной машины. Диаграмма состояния холодильного агента

а — диаграмма s — энтропия, Т — температура; б — диаграмма i — энтальпия,

lg р — давление; 1 — область жидкости; 2 — область влажного пара; 3 — область перегретого пара.(S) — абсолютная температура (T) и энтальпия (i) — логарифм давления (lg p).

По сетке наносят пограничные кривые: левую, или нижнюю, пограничную кривую, обозначаемую х=0 (х – паросодержание), и правую, или верхнюю, пограничную кривую, обозначаемую х=1. Точки нижней пограничной кривой характеризуют состояние насыщенной жидкости, т. е. жидкости, доведенной до температуры кипения. Точки, лежащие на верхней пограничной кривой, характеризуют состояние сухого насыщенного пара. Слева от нижней пограничной кривой находится область жидкости, между пограничными кривыми – область влажного пара, справа от верхней пограничной кривой – область перегретого пара. На диаграмму нанесены изобары р=const, изохоры V=const, линии постоянной энтальпии i-const, для области влажного пара – линии постоянного паросодержания х=const. Для области влажного пара линии р=constи T= const совпадают.

В диаграмме s – Т теплота, подведенная к рабочему телу или отведенная в процессе от рабочего тела, эквивалентна площади, ограниченной линией процесса, осью абсцисс и крайними ординатами. В диаграмме i – lg р (рисунок 1.3, а) сетку диаграммы образуют линии постоянной энтальпии, или изоэнтальпы (вертикальные прямые) и изобары (горизонтальные прямые); приэтом по оси ординат принят логарифмический масштаб lg р.На диаграмме нанесены пограничные кривые, а также изобары p=const, изотермы T=const, изохоры V=const, изоэнтальпы i=const , адиабаты s=const, линии постоянного паросодержания =const. В этой диаграмме тепло-подведенная в изобарном процессе и равная разности эн-1ьпий, изображается отрезком оси абсцисс.

Обратный цикл Карно. Обратный цикл Карно (рисунок 1.4) является идеальным циклом холодильной машины.

Рисунок 1.3 – Обратный цикл Карно

В качестве рабочего тела в цикле принят идеальный газ. Допущено, что подвод теплоты от источника низкой температуры к рабочему телу (процесс 4 – 1) происходит при отсутствии разности температур между ними, т. е. источник низкой температуры, и рабочее тело имеют температуру Т_о. Аналогично происходит отвод теплоты рабочего тела к источнику высокой температуры (процесс 2 – 3) при одинаковой температуре Т_к. Практически переход теплоты при таких условиях невозможен. Изучение цикла Карно очень важно, так как он показывает какое наибольшее количество холода может быть при наименьшей затрате работы в условиях Т_о и Т_к.

Цикл Карно состоит из двух адиабат и двух изотерм. В изотермическом процессе 4-1 от источника низкой температуры (охлаждаемой среды) при температуре То и давлении ро к рабочему телу подводится теплота q0. эквивалентная площади в — 4—1—а.

В адиабатном процессе 1 – 2 рабочее тело сжимается от начального давления р₀ до давления р_к, при этом температура его повышается от T_о до T_к, на сжатие затрачивается работа l_сж. В изотермическом процессе 2—3 при температуре T_к и давлении р_к рабочее тело отдает источнику высокой температуры (нагретому телу) теплоту ц_к, эквивалентную площади в—3—2—а. В процессе 3—4 рабочее тело адиабатно расширяется, совершая работу lрасш . При этом давление уменьшается от р_к до р0, а температура понижается от T_к до T₀ в результате чего рабочее тело вновь приобретает способность отводить теплоту от источника низкой температуры, и цикл повторяется. Для переноса теплоты q₀ от источника низкой температуры к источнику высокой температуры требуется работа lo=l_сжат – _lрасш. В соответствии со вторым законом термодинамики тепловой баланс холодильной машины выражается уравнением

Работа l₀ может быть выражена площадью 1-2-3-4

Эффективность холодильного цикла определяется холодильным коэффициентом

Холодильный коэффициент — это отношение количества теплоты, отведенной от источника низкой температуры, к затраченной в цикле работе, которая может быть выражена формулой

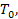
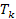
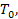
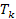
Как видно из формулы (1.2), холодильный коэффициент цикла Карно не зависит от физических свойств рабочего тела, а является лишь функцией температур и будет тем больше, чем выше и ниже . Чем больше холодильный коэффициент, тем экономичнее работа холодильной машины, т. е. тем меньше работы затрачивается для получения единицы холода. Количество теплоты qо кДж/кг, подведенной к 1 кг «холодильного агента от источника низкой температуры При работе холодильной машины, называется удельной массовой холодопроизводительностью холодильного агента.

Количество теплоты qv (в кДж/м 3 ), которое отбирает холодильный агент от источника низкой температуры, в результате чего образуется 1 м 3 пара, представляет собой объемную холодопроизводительность

где v —удельный объем образующихся паров холодильного агента, м 3 /кг.

Удельная и объемная холодопроизводительность зависят от условий работы холодильной машины, и значение их тем больше, чем выше Т_о и ниже Т’_к,

Машины, работающие по обратному циклу Карно, могут быть использованы для отопления помещений. В этом случае теплота при температуре T_о отводится от окружающей среды, а теплота q_К при температуре T_к подводится к воздуху отапливаемого помещения. Такая машина называется тепловым насосом, а цикл, по которому она работает, – циклом теплового насоса. Естественно, что цикл теплового насоса осуществляется при более высоких температурах, чем цикл холодильной машины. Эффективность этого цикла оценивается коэффициентом отопления µ

Дата добавления: 2015-11-12 ; просмотров: 7019 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

ЦИКЛЫ ХОЛОДИЛЬНЫХ УСТАНОВОК

4.1. Принцип работы холодильных установок

Холодильная установка создаёт и поддерживает в теплоизолированном помещении (холодильной камере) температуру Т₀, которая ниже температуры окружающей среды Т_C. При наличии разности температур через изоляцию в холодильную камеру поступает теплота из окружающей среды в результате естественного теплообмена, поэтому холодильная установка для поддержания температуры Т₀ должна отводить эту теплоту. Таким образом, холодильная установка должна отбирать теплоту при низкой температуре и передавать её окружающей среде при более высокой температуре.

Для отвода теплоты из охлаждаемого помещения необходимо затрачивать работу либо теплоту. Если в холодильной установке затрачивается механическая (электрическая) энергия для работы компрессора, установка называется компрессорной, а в случае затраты теплоты –– теплоиспользующей.

Уравнение теплового баланса холодильной установки

Рис. 4.1. Обратимый обратный цикл Карно в координатах T,s.

Для минимизации работы, затрачиваемой на перенос теплоты от более холодного тела к более нагретому, все термодинамические процессы в установке должны быть обратимыми. Поэтому если температура охлаждаемого объекта Т₀ постоянна, то идеальным циклом холодильной установки является обратимый обратный цикл Карно, протекающий между температурами Т₀ и Т_C (рис 4.1). Если же холод требуется при переменных температурах, то цикл Карно, в котором подвод теплоты должен происходить при постоянной и наиболее низкой температуре, не будет идеальным. В последнем случае цикл Карно требует больше работы, чем цикл, в котором теплота подводится обратимо при переменной температуре.

Из диаграммы Т,s (рис. 4.1) видно, что для обратимого обратного цикла Карно теплота, подводимая к рабочему телу, равна q₀ = T₀(s₁–s₄), а отводимая от рабочего тела в окружающую среду по абсолютной величине равна |q₂| = T_С(s₂–s₃). В соответствии с первым законом термодинамики абсолютная величина работы, затраченной в этом цикле, равна

(4.1)

то есть эквивалентна площади цикла 1–2–3–4–1.

Эффективность работы холодильной установки характеризует холодильный коэффициент ε=q₀/|l|, который для обратимого обратного цикла Карно равен

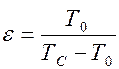(4.2)

Для теплообмена между охлаждаемым помещением и рабочим телом температура последнего должна быть ниже, чем T₀, а при отдаче теплоты окружающей среде температура рабочего тела должна быть больше Т_С. Вследствие конечной разности температур при теплообмене возникает внешняя необратимость холодильного цикла. Кроме того, сжатие и расширение рабочего тела нельзя осуществлять изоэнтропно ввиду потерь на трение при течении рабочего тела в элементах установки. Эти потери приводят к внутренней необратимость цикла. По указанным причинам затрачиваемая работа в действительном холодильном цикле больше, а холодильный коэффициент меньше, чем в обратимом цикле Карно.

Холодильная установка работает в направлении, противоположном естественному процессу теплообмена, но эффект

её работы не является количественно прямо противоположным эффекту теплообмена. При естественном теплообмене от окружающей среды в охлаждаемое помещение необратимо передаётся теплота q₀, а холодильная установка передаёт окружающей среде бὀльшее количество теплоты: q₂ = q₀ + |l|.

4.2 Схема и цикл воздушной холодильной установки

Принципиальная схема холодильной установки, в которой рабочим телом является воздух (либо другой идеальный газ), представлена на рис. 4.2. Основными элементами установки являются два механизма: компрессор 1 и детандер 3, а также два теплообменных аппарата: холодильник 2 и рефрижератор 4. В современных воздушных холодильных установках используются турбокомпрессоры и турбодетандеры.

Компрессор сжимает изоэнтропно воздух, имеющий параметры р₁ и Т₁, до давления р₂ и температуры Т₂, превышающей температуру окружающей среды Т₃. Сжатый воздух в холодильнике отдаёт теплоту охлаждающей среде, и его температура в становится равной Т₃. Затем воздух расширяется изоэнтропно в детандере до давления р₁, при этом его температура уменьшается до значения Т₄ и становится ниже, чем температура Т₁ в охлаждаемом помещении. После детандера воздух подаётся в рефрижератор, где при давлении р₁ отбирает теплоту из охлаждаемого помещения, нагреваясь в пределе до температуры Т_1, а затем всасывается компрессором.

Теоретический цикл воздушной холодильной установки 1–2–3–4, состоящий из двух изобар и двух изоэнтроп (цикл Лоренца), изображён в координатах p,v и Т,s на рис. 4.3. Его можно рассматривать как обратный цикл газотурбинной установки с подводом теплоты при постоянном давлении и адиабатным сжатием воздуха в компрессоре (цикл Брайтона).

Приняв изобарную теплоемкость воздуха с_р0 постоянной, получим следующие выражения для величин, характеризующих цикл Лоренца:

– количество теплоты, отбираемое 1 килограммом рабочего тела, подаваемого в охлаждаемое помещение (удельная массовая холодопроизводительность):

;

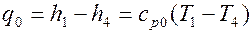(4.3)

– работа, затрачиваемая в цикле (по абсолютной величине):

;

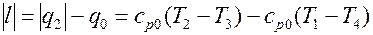(4.4)

– холодильный коэффициент цикла

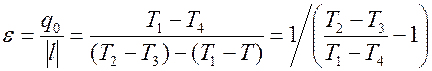(4.5)

Поскольку изоэнтропы 1–2 и 3–4 расположены между одинаковыми изобарами, справедливо следующее равенство

Рис. 4.3. Цикл воздушной холодильной установки.

(4.6)

С учетом (4.6) можно представить выражение (4.5) в виде

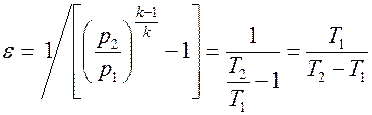(4.7)

Следовательно, холодильный коэффициент ε газовой холодильной установки зависит только от отношения давлений (либо температур) рабочего тела при изоэнтропном сжатии в компрессоре: чем меньше это отношение, тем выше ε.

Уравнение (4.7) имеет такой же вид, как и уравнение (4.2) для холодильного коэффициента обратимого обратного цикла Карно. Однако это сходство внешнее, так как в обратном цикле Карно Т_С –– температура окружающей среды, а в цикле воздушной холодильной машины Т₂ –– температура газа после компрессора, которая выше температуры окружа-ющей среды Т_3. Поэтому при равных температурах охлаждаемого объекта Т₁ холодильный коэффициент обратного цикла Карно выше такого коэффициента цикла Лоренца. Этот же вывод можно сделать из совместного изображения обоих циклов на диаграмме Т,s: при одинаковых значениях Т₁ и Т₃ у цикла Карно 1–2’–3–-4′ удельная холодопроизводительность q₀ больше, а затрачиваемая работа меньше (см. рис. 4.3б).

В обычной газовой холодильной установке нельзя осуществить обратный цикл Карно, так как изобарные процессы теплообмена в холодильнике и рефрижераторе протекают при переменной температуре газа. В принципе возможен обобщенный обратный цикл Карно, если ввести регенеративный теплообмен между потоками газа, выходящими из компрессора и детандера, и поддерживать постоянные значения температуры газа при сжатии и расширении в этих механизмах, но обеспечить в детандере такое условие трудно.

При постоянных температурах окружающей среды Т₃ и охлаждаемого помещения Т₁ процессы теплообмена в газовой установке протекают при конечной переменной разности температур. Поэтому цикл Лоренца внешне необратим, хотя процессы сжатия и расширения газа –– изоэнтропные.

Действительный холодильный коэффициент данного цикла меньше теоретического, так как потери в компрессоре и детандере увеличивают затрату работы. К тому же потери в детандере снижают удельную холодопроизводительность, поскольку реальная температура газа в конце расширения выше теоретической. Газовые холодильные установки используются для получения холода при низких и при переменных температурах, в частности, для сжижения и разделения газовых смесей, которые кипят на изобаре при переменной температуре. Эффективность этих установок повышается при использовании регенеративного теплообмена между потоками газа, выходящим из рефрижератора и поступающим в детандер.

4.3. Схема и цикл парокомпрессорной холодильной

Недостатки газовых холодильных установок устранены в парокомпрессорных, где рабочее тело –– реальный газ. Изобарные процессы теплообмена при испарении (кипении) и конденсации реального газа протекают при постоянных температурах, что приближает теоретический цикл установки к обратному циклу Карно. Благодаря фазовым превращениям рабочего тела теплообменные аппараты могут работать при небольших разностях температур теплообменивающихся сред, и это уменьшает внешнюю необратимость цикла.

Парокомпрессорные холодильные установки компактнее газовых, так как благодаря высокой плотности насыщенного пара хладагента (по сравнению с плотностью газа) количество теплоты, воспринимаемое 1м 3 рабочего тела, поступающего в компрессор (удельная объёмная холодопроизводительность), в парокомпрессорных установках больше, чем в газовых. К тому же в парокомпрессорных установках не применяются детандеры, так как работа расширения жидкости в детандере мала и ею можно пренебречь, заменив изоэнтропное расширение жидкости процессом её дросселирования.

Хладагенты, используемые в парокомпрессорных холодильных установках, должны иметь температуру кипения при атмосферном давлении от –20 до –50ºС для того, чтобы в установке при обычных условиях работы не было вакуума, способствующего попаданию воздуха в систему. Критическая температура хладагента должна быть выше температуры окружающей среды, чтобы процесс отвода теплоты в эту среду протекал преимущественно в двухфазной области при Т = const. Критическое давление хладагента должно быть умеренным во избежание высокого давления сжатия пара.

Помимо термодинамических требований хладагентам предъявляют экологические требования. При попадании в атмосферу они не должны разрушать её озоновый слой и создавать парниковый эффект. Удовлетворить этим требованиям сложно, так как многие хладагенты, безопасные для озонового слоя, имеют плохие показатели по парниковому эффекту. Поэтому продолжаются поиски оптимальных рабочих тел для парокомпрессорных холодильных установок, основанные на использовании природных (NH₃, CO₂, C₃H₈) и озонобезопасных (CH₂F_2, CH₂F₄, C₂HF₅) хладагентов и их смесей.

Рис. 4.4. Схема одноступенчатой парокомпрессорной холодильной установки холодильной установки.

На рис. 4.4 приведена принципиальная схема простейшей одноступенчатой парокомпрессорной холодильной установки, состоящей из четырёх основных элементов: компрессора 1, конденсатора 2, дроссельного вентиля 3 и испарителя 4. В конденсаторе благодаря работе компрессора и наличию дроссельного вентиля поддерживается давление р₂, которому соответствует температура конденсации хладагента, превышающая температуру охлаждающей среды на 5–8ºС. В испарителе давление должно быть таким, чтобы температура кипения хладагента была ниже температуры охлаждаемого объекта на 8–16ºС (в зависимости от системы охлаждения).

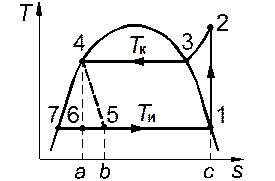Рис.4.5. Цикл одноступенчатой парокомпрессорной холодильной установки.

Процессы в простейшей холодильной установке протекают следующим образом. Компрессор всасывает из испарителя насыщенный пар хладагента при давлении р₁ и изоэнтропно сжимает его до давления р₂ (процесс 1–2, рис. 4.5). Из компрессора перегретый пар поступает в конденсатор, где сначала охлаждается до температуры насыщения, соответствующей давлению р₂ (процесс 2–3), а затем конденсируется (процесс 3–4). При этом теплота отдаётся охлаждающий воде либо воздуху, то есть окружающей среде. Жидкий хладагент в состоянии насыщения подаётся в дроссельный вентиль, где его давление понижается до давления р₁, поддерживаемого в испарителе (процесс 4–5). При адиабатном дросселировании температура хладагента понижается, а значения его энтальпии в начале и в конце процесса совпадают, поэтому точки 4 и 5 соединены кривой h = const. После дроссельного вентиля влажный пар хладагента поступает в испаритель, где превращается в насыщенный пар (процесс 5–1) за счёт подвода теплоты, отбираемой от охлаждаемого объекта.

Цикл парокомпрессорной холодильной установки 1–2–3–4–5–1 (см. рис. 4.5) рассматривают как условный, так как среди его процессов есть неравновесный процесс дросселирования 4–5. Площадь цикла не соответствует затрачиваемой работе, равной технической работе компрессора |l_к| = h₂ – h₁. При умеренных давлениях, характерных для парокомпрессорных установок, изобары жидкости можно считать совпадающими с пограничной кривой жидкости. Тогда работа компрессора изображается на диаграмме T,s площадью 1–2–3–4–7–1, которая больше площади цикла. Теплота, подводимая к килограмму рабочего тела в испарителе (удельная массовая холодопроизводительность) равна q₀ = h₁ – h₅ = h₁–h₄. Холодильный коэффициент данного цикла равен:

(4.8)

Значение ε цикла парокомпрессионных установок на 15÷20 % меньше значения ε обратного цикла Карно при тех же температурах испарения и конденсации.

Замена в парокомпрессорной установке детандера дроссельным вентилем уменьшает удельную холодопроизводительность, так как необратимый процесс дросселирования 4–5 приводит к росту энтропии. Эта замена также увеличивает работу, затрачиваемую в цикле. Совместное действие двух факторов уменьшает холодильный коэффициент. В то же время из диаграммы T,s видно (см. рис. 4.5), что для условного цикла с дросселированием 1–2–3–4–5–1 и цикла 1–2–3–4–6–1 с изоэнтропным расширением насыщенной жидкости в детандере количество теплоты q₂, отводимой в конденсаторе в окружающую среду, одинаково. В соответствии со первым законом термодинамики |q₂|=q₀+|l|. Поэтому уменьшение удельной холодопроизводительности вследствие дросселирования равно дополнительно затрачиваемой работе (то есть работе детандера, теряемой в цикле с дросселированием).

Несмотря на потери от дросселирования, цикл с дросселированием рентабельнее цикла с детандером, если учесть затраты на изготовление установки, трудности эксплуатации и регулирования. К тому же при дросселировании в двухфазной области энтропия хладагента возрастает незначительно, то есть потеря холодопроизводительности, которой на диаграмме T,s соответствует площадь а-6-5-b, относительно невелика. Поэтому только в установках большой холодопроизводительности заменяют дроссельный вентиль турбодетандером.

Эффективно повышает удельную холодопроизводительность переохлаждение жидкого хладагента перед дросселированием путём регенеративного теплообмена между жидкостью, выходящей из конденсатора, и паром, поступающим в компрессор. Принципиальная схема такой установки представлена на рис. 4.6. По сравнению с простейшей схемой здесь добавлен регенеративный теплообменник 5, остальные элементы те же, что и на рис. 4.4. Регенеративный теплообмен применяется в большинстве холодильных установок, так как он не только повышает холодопроизводительность, но и улучшает условия работы компрессора, предотвращая возможность возникновения так называемого “влажного хода”, приводящего к гидравлическому удару в компрессоре.

Рис. 4.6. Схема парокомпрессорной холодильной установки с регенерацией теплоты.

Цикл рассматриваемой холодильной установки представлен на рис. 4.7. На участках 4–5 изобары р₂ и 7–1 изобары р₁ осуществляется регенеративный теплообмен между жидкостью и паром хладагента. Поэтому удельная холодопроизводительность в этом цикле равна h₇ – h₆ и изображается площадью а–6–7–с под изобарой р₁, а её увеличение по сравнению с обычным циклом –– площадью а–6–4′–b. Холодильный коэффициент рассматриваемого цикла равен

(4.9)

Рис. 4.7. Цикл парокомпрессорной холодильной установки с регенерацией теплоты.

Значение h₇ для пара определяют по таблице термодинамических свойств хладагента в состоянии насыщения при давлении р₁, значение h₅ для жидкости –– по этой же таблице при температуре t₅ (так как свойства жидкости мало зависят от давления). Значение h₁ рассчитывают из уравнения теплового баланса регенеративного теплообменника

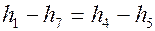(4.10)

Рассчитав значение h₁, находят точку 1 на изобаре р₁, проводят из неё изоэнтропу до пересечения с изобарой р₂, определяют точку 2 и значение энтальпии h₂ . Значение h₂ можно определить также по таблице термодинамических свойств перегретого пара хладагента из условия s₂=s₁ при известном давлении конденсации. В результате получают все данные, необходимые для расчёта холодильного коэффициента.

Повышение температуры пара перед компрессором при регенеративном теплообмене приводит к росту температуры конца сжатия и увеличению работы компрессора. Поэтому применение регенеративного теплообмена может увеличить либо уменьшить теоретическое значение холодильного коэффициента в зависимости от термодинамических свойств хладагента и интервала температур, в котором работает холодильная установка. В то же время регенеративный теплообмен однозначно улучшает эксплутационные показатели холодильных установок и повышает действительное значение ε.

4.4. Теплоиспользующие холодильные установки

В теплоиспользующих холодильных установках для получения холода используется непосредственно теплота низкого потенциала. Это возможно потому, что тепловая энергия источника, температура которого выше температуры окружающей среды, обладает работоспособностью (по отношению к окружающей среде). Как правило, источниками теплоты для этих установок являются так называемые вторичные энергоресурсы. В судовых условиях используется теплота, отводимая от уходящих газов двигателей внутреннего сгорания и котельных установок либо от воды, охлаждающей теплообменные аппараты энергетической установки.

К теплоиспользующим холодильным установкам относятся пароэжекторные и абсорбционные. В пароэжекторной установке процесс отсасывания пара из испарителя и его сжатия протекает в струйном насосе (эжекторе);её принципиальная схема представлена на рис.4.8. Основные элементы установки: парогенератор 1, насос 2, дроссельный вентиль 3, испаритель 4, эжектор 5 и конденсатор 6. Рабочий пар (давления 0,5–0,8 МПа) из парогенератора 1 поступает в сопло Лаваля эжектора 5. Там потенциальная энергия давления пара преобразуется в кинетическую энергию потока, скорость которого достигает 1000–1200 м/с. При этом давление пара, выходящего из сопла в смесительную камеру эжектора, понижается до значения, которое меньше давления в испарителе. Благодаря этому холодный пар, образующийся в испарителе 4, поступает в смесительную камеру и смешивается с рабочим паром.

Рис. 4.8. Принципиальная схема пароэжекторной холодильной установки.

Смесь паров поступает в диффузор эжектора, где кинетическая энергия потока преобразуется в потенциальную. При этом скорость потока уменьшается, а давление повышается до значения, соответствующего температуре конденсации (которая выше температуры окружающей среды). Затем смесь конденсируется в конденсаторе 6 и на выходе из него разделяется на два потока. Один поток насосом 2 подаётся в парогенератор 1, а второй через дроссельный вентиль 3 поступает в испаритель 4, где кипит при температуре, которая ниже температуры охлаждаемого объекта, и отбирает теплоту от него.

Итак, в пароэжекторной холодильной установке отсасывание пара из испарителя и его сжатие до давления конденсации осуществляется не компрессором, а паровым эжектором. Если для привода компрессора используется механическая (электрическая) энергия, то для работы эжектора –– кинетическая энергия пара, образующегося в парогенераторе за счёт подвода теплоты. Следовательно, в пароэжекторной установке исключён ряд ступеней преобразования энергии, имеющих место в парокомпрессорной: тепловая – механическая – электрическая – механическая – тепловая. Как известно, всякий процесс преобразования энергии сопровождается потерями, отрицательно влияющими на конечный эффект.

В данной установке, по существу, совмещены прямой и обратный циклы. В прямом тепловая энергия, отданная отработавшими газами либо охлаждающей водой рабочему пару, преобразуется в кинетическую энергию потока пара. В обратном цикле эта энергия используется для отсасывания пара из испарителя и повышения давления смеси паров, подаваемой в конденсатор. Таким образом, тепловая энергия низкого потенциала непосредственно используется для переноса теплоты от охлаждаемого объекта в окружающую среду.

Процессы теплопередачи в установке происходят на трёх температурных уровнях: низком –– при подводе теплоты к хладагенту в испарителе, среднем –– при отводе теплоты в окружающую среду в конденсаторе и высоком –– при подводе теплоты к рабочему пару в парогенераторе.

Рабочим телом пароэжекторных холодильных установок чаще всего является водяной пар, удельный объём которого при температурах, близких к 0ºС, весьма велик. Всасывание больших объёмов пара поршневыми либо центробежными компрессорами проблематично, поэтому в таких установках применяется компактный аппарат –– эжектор. С термодинамической точки зрения цикл пароэжекторной холодильной установки менее совершенен, чем цикл парокомпрессорной установки, в связи с необратимостью процесса смешения потоков пара в эжекторе. Однако благодаря простоте, компактности и возможности использования вторичных энергоресурсов пароэжекторные установки находят применение в системах кондиционирования воздуха. В качестве хладагента в таких установках могут также применяться фреоны, что позволит уменьшить размеры установок и эффективнее использовать теплоту низкого потенциала (порядка 70ºС).

Термодинамическую эффективность цикла пароэжекторной установки характеризует коэффициент теплоиспользования (тепловой коэффициент). Если пренебречь работой насоса, которая в данном цикле незначительна, то тепловой коэффициент определяется по формуле:

(4.11)

где Q₀ –– теплота, отводимая от охлаждаемого объекта,

Q₁ –– теплота, подводимая к пару в парогенераторе.

Выражение (4.1) можно преобразовать к виду:

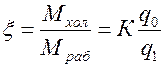(4.12)

где К –– коэффициент эжекции (отношение количеств холод- ного и рабочего пара),

q₀ –– удельная холодопроизводительность,

q₁ –– удельная затрата теплоты.

В действительном цикле значение К меньше теоретического в основном вследствие необратимости процессов в эжекторе.

В абсорбционных холодильных установках используется способность жидкого раствора абсорбировать (поглощать всем объёмом) пар низкокипящего растворяемого вещества, даже если температура ненасыщенного жидкого раствора выше температуры пара. В качестве рабочих веществ в этих установках применяют бинарные растворы, удовлетворяющие требованиям неограниченной растворимости компонентов друг в друге и возможно бὀльшей разности температур кипения компонентов при одинаковом давлении. Компонент, кипящий при более низкой температуре, выполняет функции хладагента, а кипящий при более высокой температуре –– функции абсорбента. Пар, образующийся при кипении раствора, содержит в основном низкокипящий компонент –– хладагент, а жидкость, образующаяся при конденсации раствора, содержит в основном высококипящий компонент.

Рис. 4.9. Принципиальная схема абсорбционной холодильной установки.

Схема абсорбционной холодильной установки приведена на рис. 4.9. В качестве рабочего тела часто используется водо-аммиачный раствор, а хладагентом является аммиак. Жидкий аммиак поступает из конденсатора 1 в дроссельный вентиль 2 при температуре конденсации Т₁ и соответствующем давлении р₁. При дросселировании до давления р₂, поддерживаемого в испарителе 3, температура аммиака снижается до значения Т₂, соответствующего этому давлению. В испарителе влажный пар аммиака превращается в насыщенный за счёт притока теплоты Q₀ от охлаждаемого объекта.

Насыщенный пар аммиака при температуре Т₂ поступает в абсорбер 4, куда из парогенератора 6 через дроссельный вентиль 7 подаётся обеднённый раствор аммиака в воде, имеющий более высокую температуру Т₄. Этот раствор с незначительным содержанием легкокипящего компонента абсорбирует пар аммиака. При абсорбции выделяется теплота q_абс, которая отводится охлаждающей водой во избежание повышения температуры раствора и уменьшения растворимости аммиака в нём. Из абсорбера выходит обогащённый раствор при температуре Т₃ (Т₂ 0 С.

4.5. Тепловые насосы и теплофикационные

Одной из разновидностей холодильных установок являются тепловые насосы –– холодильные установки, используемые для подвода теплоты к обогреваемому объекту (помещению). Такие установки как бы «перекачивают» теплоту из холодного источника в горячий. По существу, всякая холодильная установка является тепловым насосом, но так называют те установки, которые предназначены для нагрева теплоприёмника (помещения). Тепловые насосы отбирают от окружающей среды теплоту q₀, за счёт затраты работы в цикле повышают её температурный потенциал и отдают теплоприёмнику, добавляя теплоту, равную затрачиваемой работе.

Эффективность теплового насоса оценивается отопительным коэффициентом μ, представляющим собой отношение количества теплоты q₂, отданной нагреваемому объекту, к работе |l|, затраченной в цикле

(4.15)

Из соотношения (4.15) следует, что эффективность теплового насоса значительно выше эффективности обычных электронагревательных приборов, у которых μ = 1. Так, если в тепловом насосе осуществляется обратный обратимый цикл Карно при температуре окружающей среды 0ºС и температуре нагреваемого помещения 25ºС, то отопительный коэффициент равен 11,9. Значения отопительного коэффициента реальных тепловых насосов вследствие осуществления менее совершенных циклов, характеризуемых внешней и внутренней необратимостью, составляют от 3 до 5, уменьшаясь по мере понижения температуры окружающей среды.

Идея теплового насоса была высказана английским физиком Кельвиным еще в 1852 г., а начало их применения относится к 30-тым годам прошлого столетия. Широкому внедрению столь эффективного метода отопления помещений препятствуют две причины. Первая –– необходимость капиталовложений на изготовление тепловых насосов. Вторая причина –– то обстоятельство, что при получении электроэнергии, обеспечивающей работу теплового насоса, эффективный к.п.д. составляет примерно 35%. При таком значении к.п.д. фактическая экономия исходного топлива (угля, газа) от использования тепловых насосов, потребляющих электроэнергию, оказывается втрое меньше значения, определяемого на основании отопительного коэффициента.

Весьма эффективным с практической и термодинамической точек зрения является комбинированный цикл трансформатора теплоты –– теплофикационный холодильный цикл. В этом цикле одновременно получают и используют холод на низкотемпературном уровне и теплоту на высокотемпературном. Теплота q₀, отбираемая от охлаждаемого объекта, отдаётся не окружающей среде, а потребителю (например, обогреваемому помещению) при температуре, превышающей тем-пературу окружающей среды. При этом обеспечиваются отопление помещений, технологические нужды и другие аналогичные потребности в теплоте. Отданная потребителю при конденсации хладагента теплота q₂ равна сумме q₀+|l|.

Поскольку в комбинированном цикле одновременно получают холод и теплоту, его термодинамическую эффективность характеризуют два коэффициента –– холодильный и отопительный. Холодильный коэффициент такого цикла меньше, чем цикла с конденсацией хладагента при температуре, близкой к температуре окружающей среды (в связи с бὀльшей затратой работы). Однако это вполне компенсируется тем, что теплота конденсации хладагента не отдаётся окружающей среде, а полезно используется потребителем.