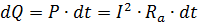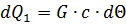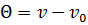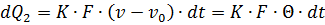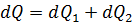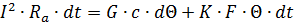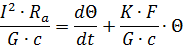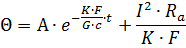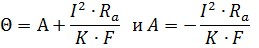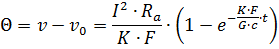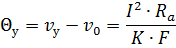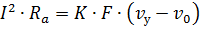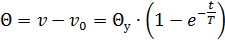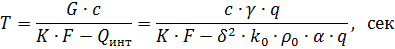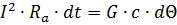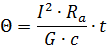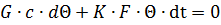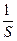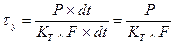Нагрев токоведущих частей и уравнение теплового баланса

При работе токоведущих частей выделяют продолжительный и кратковременный режимы нагрева. Оборудование электростанций и подстанций в нормальных условиях работает в продолжительном режиме, а при коротких замыканиях в кратковременном режиме нагрева.

Процесс нагрева проводников в этих режимах можно описать с помощью уравнения теплового баланса. Составим это уравнение.

Пусть по длинному проводнику, имеющему сопротивление R, удельную теплоёмкость c, массу m и помещённому во внешнюю среду с температурой θ_ср протекает ток I. Для малого интервала времени dt можно составить уравнение теплового баланса:

. (1)

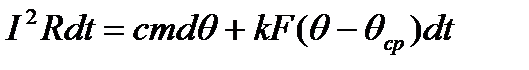
Здесь левая часть уравнения определяет тепло, которое выделилось в проводнике за время dt, первый член правой части определяет тепло расходованное на повышение температуры проводника на dθ градусов за время dt. Второй член правой части определяет тепло выделившееся в окружающую среду за время dt при условии, что k – коэффициент теплоотдачи, учитывающий все её виды (теплопроводность, конвекция, излучение), F – поверхность проводника, а θ – температура проводника.

Продолжительный режим нагрева – это режим с постоянной нагрузкой в течение неограниченного времени, когда проводник или аппарат находится в установившемся тепловом состоянии, достигая неизменной температуры.

Каждый проводник и изоляционный материал имеют допустимые температуры в продолжительном режиме θ_доп.дл. Например, изоляция в зависимости от класса имеет следующие допустимые температуры:

класс	У	А	Е	В	Р	Н	G
θ_доп.дл , 0 С	>180

Для неизолированных медных и алюминиевых проводников длительно допустимая температура 70 о С.

Уравнение теплового баланса в продолжительном режиме примет вид:

. (2), т.к. при некоторой установившейся температуре проводника θ_уст его температура не изменяется и, следовательно, dθ=0. На основании (2) можно получить связь между током в проводнике I в установившемся режиме и его температурой θ_уст:

.(3)

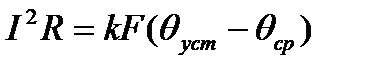
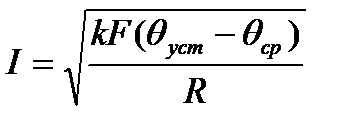
Номинальным называют длительно допустимый ток проводника, при котором проводник достигает длительно допустимой температуры θ_доп.дл при стандартизированной температуре окружающей среды θ_ср.ст.

Среда	_{СТАНДАРТИЗИРОВАННАЯ ТЕМПЕРАТУРА θср.ст}, о С
Воздух для проводников	+25
Воздух для аппаратов	+35
Земля	+15
Вода	+15

На основании (3) можно получить выражение для I_ном:

. (4)

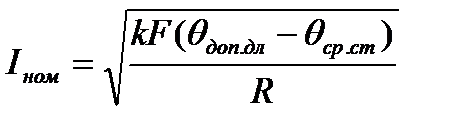
Если температура окружающей среды не равна стандартной, то говорят о допустимом токе проводника при данных условиях:

. (5)

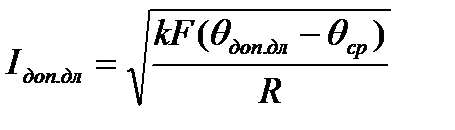
Если взять отношение допустимо длительного и номинального токов, то можно получить связь между этими токами:

. (6)

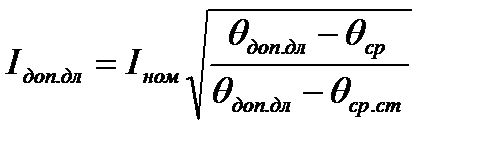
Из отношения произвольного тока в проводнике I и номинального тока можно определить установившуюся температуру проводника θ_уст при произвольной температуре среды θ_ср, отличной от стандартной:

. (7)

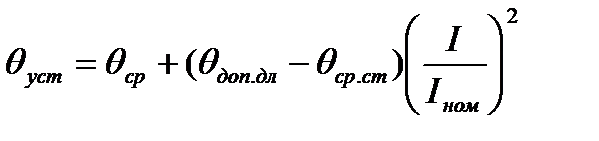
Нагрев проводников в кратковременном режиме. Критерием термической стойкости проводника в этом режиме является температура его нагрева токами КЗ. Проводники (и аппараты) считаются термически стойкими, если их конечная температура в процессе КЗ не превышает допустимой величины θ_{к доп}.

Определить конечную температуру нагрева проводника θ_к в процессе КЗ можно с помощью уравнения теплового баланса, которое из-за краткости режима КЗ, когда можно пренебречь выделением тепла в окружающую среду, примет вид:

. (8)

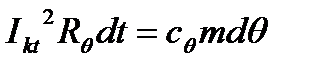
Здесь I_kt – ток КЗ (действующее значение), который с течением времени t может изменяться;

— активное сопротивление проводника при текущей температуре θ,

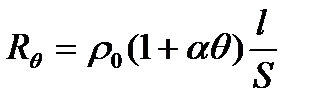
ρ₀ – удельное сопротивление проводника при θ=0 0 С;

l и S – длина и сечение проводника;

α – температурный коэффициент сопротивления;

— теплоёмкость проводника при температуре θ,

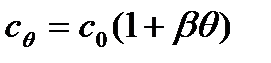
β – температурный коэффициент теплоёмкости;

m=γlS – масса проводника,

γ – плотность проводника.

Произведем подстановку в уравнение (8) рассмотренных выражений и проинтегрируем по соответствующим переменным:

. (9)

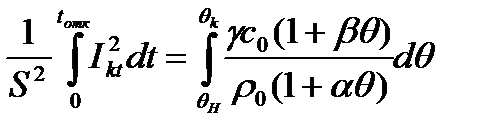
Здесь t_отк – время с начала КЗ до отключения,

Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

θ_н – начальная температура проводника (перед КЗ),

θ_к – конечная температура проводника (в момент отключения КЗ).

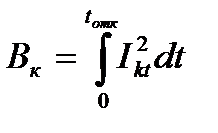
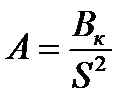
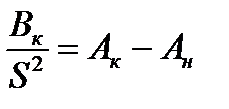
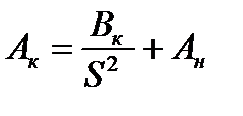
Величина пропорциональная количеству тепла, выделенного при КЗ, носит название теплового импульса, а величина носит название удельного теплового импульса. Значение интеграла в правой части соответствующее начальной температуре θ_н обозначим А_н, а конечной θ_k – А_к. Теперь можно записать:

или .

Величина А есть сложная функция температуры проводника и приводится в справочниках в виде графиков для проводников из различных материалов.

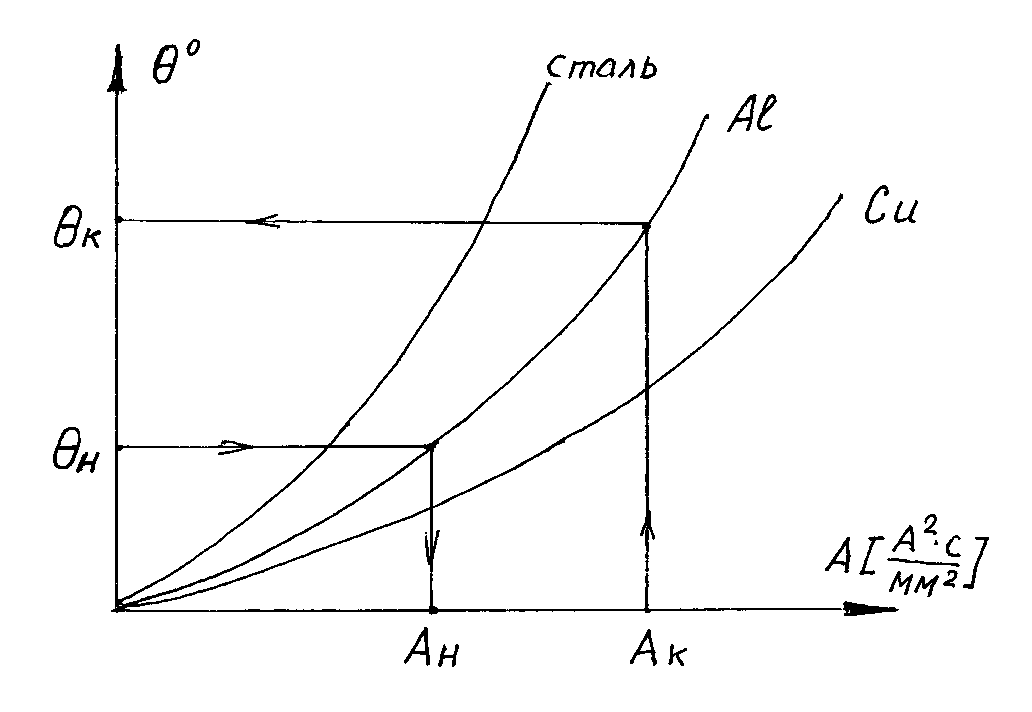
Рассмотрим, как с помощью этих графических зависимостей (Рис.9.1) определить конечную температуру проводника.

Рис. 9.1 Кривые для определения конечной температуры проводников.

В качестве начальной температуры θ_н принимаемустановившуюся температуру θ_уст проводника перед КЗ, которую вычисляем по ранее приведенной формуле (7), где I максимальный ток нагрузки в проводнике.

Зная θ_н, по кривой A=f(θ) определим А_н. Вычислив В_к, определим 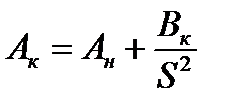, а затем по кривой определим конечную температуру θ_к.Если будет выполняться условие θ_к≤θ_{к доп}, то проводник в данных условиях будет термически стоек.

Таким образом, чтобы с помощью кривых A=f(θ) определить термическую стойкость проводников необходимо уметь вычислять тепловой импульс тока КЗ В_к. Так как ток КЗ в общем случае содержит периодическую и апериодическую составляющие, то и тепловой импульс В_к представляют состоящим из двух составляющих: В_кп – определяется переменной составляющей тока КЗ и В_ка – определяется апериодической составляющей тока КЗ. В_к≈В_{к п}+В_{к а}.

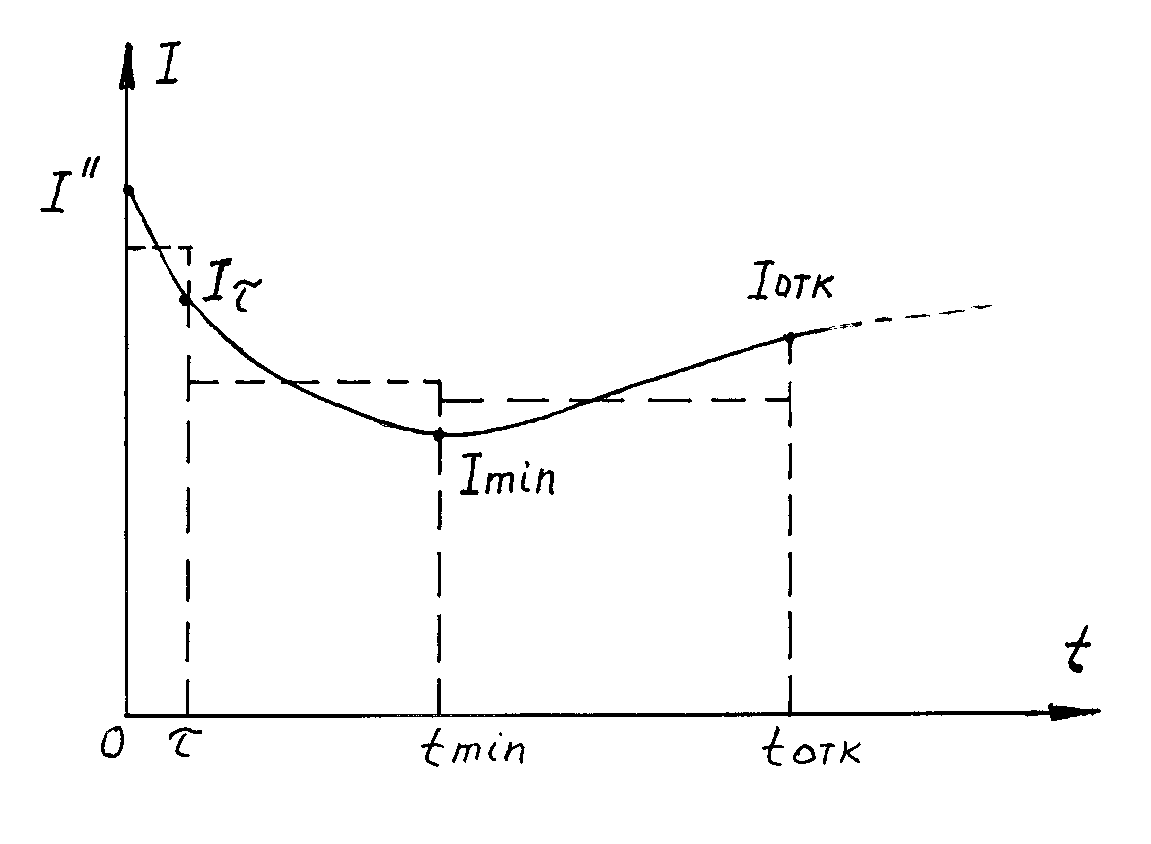
При КЗ недалеко от генераторов (КЗ на выводах генераторов, на сборных шинах распредустройств станций) действующее значение периодической составляющей тока КЗ из-за переходных процессов в генераторах и действия систем возбуждения генераторов изменяется во времени (Рис9.2). Это изменение необходимо учитывать при расчёте теплового импульса от периодической составляющей тока КЗ В_{к п}.

Рис. 9.2 Кривая изменения переменной составляющей тока КЗ для вычисления В_кп.

В расчете В_{к п} участвуют в общем случае следующие токи:

I ’’ – сверхпереходный ток КЗ;

I_τ – периодический ток КЗ в момент начала расхождения контактов выключателя;

I_min – минимальное значение периодического тока КЗ;

I_отк – периодический ток КЗ на момент отключения.

Время начала расхождения контактов выключателя τ=t_св+t_рз _min, здесь t_св – собственное время выключателя, а t_рз _min – минимальное время срабатывания основных защит в цепи выключателя (при отсутствии данных принимается 0,01 с).

Время отключения КЗ t_отк=t_во+t_рз _max, здесь t_во – время отключения выключателя t_рз _max – максимальное время срабатывания резервных защит в цепи выключателя.

Расчет В_кп основан на аппроксимации площади под кривой I 2 (t) прямоугольниками. При этом рассматриваются два случая:

;

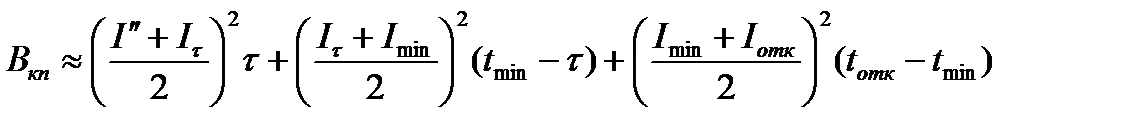
Апериодическая составляющая тока КЗ, возникнув в первый момент КЗ, затухает по экспоненциальному закону с постоянной времени петли КЗ Т_а. Можно показать, что при t_отк>Т_а тепловой импульс от апериодической составляющей можно принять В_ка≈I ’’2 Т_а.

Проверка термической стойкости аппаратов производится не по допустимой температуре, а по допустимому тепловому импульсу. Для этого в справочниках приводится ток термической стойкости I_тер и время его протекания t_тер. По ним можно вычислить допустимый тепловой импульс B_кдоп=I 2 _тер t_тер. Условием термической стойкости аппарата будет выполнение соотношения В_к≤В_{к доп}.

Аппараты и токоведущие части в цепях генераторов из-за длительного процесса гашения поля генератора при его отключении проверяют при условии, что t_отк=4с.

\|	следующая лекция ==>
Основные свойства связующих	\|	Мұғалімнің кәсіби өзін-өзі тәрбиелеуі

Дата добавления: 2016-02-09 ; просмотров: 5437 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Нагрев токоведущих частей при длительном протекании тока

Основные условия нагрева и охлаждения электрооборудования рассмотрим на примере однородного проводника, охлаждающегося равномерно со всех сторон.

Если через проводник, имеющий температуру окружающей среды, проходит ток, то температура проводника постепенно повышается, так как вся энергия потерь при прохождении тока переходит в тепло.

Скорость нарастания температуры проводника при нагреве током зависит от соотношения между количеством выделяющегося тепла и интенсивностью его отвода, а также теплопоглощающей способности проводника.

Количество тепла, выделенного в проводнике в течение времени dt, будет составлять:

Видео:ЕГЭ физика. Уравнение теплового баланса (термодинамика)Скачать

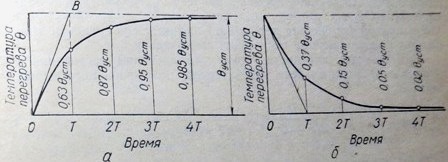
где I — действующее значение тока, проходящего по проводнику, а; Ra — активное сопротивление проводника при переменном токе, ом; Р—мощность потерь, переходящих в тепло, вm. Часть этого тепла идет на нагрев проводника и повышение его температуры, а остальное тепло отводится с поверхности проводника за счет теплоотдачи.

Энергия, идущая на нагрев проводника, равна

где G — вес токоведущего проводника, кг; с — удельная теплоемкость материала проводника, em•сек/кг•град; Θ — перегрев — превышение температуры проводника по отношению к окружающей среде:

v и vо—температуры проводника и окружающей среды, °С.

Энергия, отводимая с поверхности проводника в течение времени dt за счет теплоотдачи, пропорциональна превышению температуры проводника над температурой окружающей среды:

где К — общий коэффициент теплоотдачи, учитывающий все виды теплоотдачи, Вm/см2 °С; F — поверхность охлаждения проводника, см2,

Уравнение теплового баланса за время неустановившегося теплового процесса можно записать в следующем виде:

Для условий нормального режима, когда температура проводника изменяется в небольших пределах, можно принять, что R, с, К представляют собой постоянные величины. Кроме того, следует учесть, что до включения тока проводник имел температуру окружающей среды, т. е. начальное превышение температуры проводника над температурой окружающей среды равно нулю.

Решение этого дифференциального уравнения нагрева проводника будет

где А — постоянная интегрирования, зависящая от начальных условий.

При t = 0 Θ = 0, т. е. в начальный момент нагреваемый проводник имеет температуру окружающей среды.

Тогда для t = 0 получаем

Подставляя значение постоянной интегрирования А, получаем

Из этого уравнения следует, что нагрев токоведущего проводника происходят по экспоненциальной кривой (рис. 1). Как видно, с изменением времени подъем температуры проводника замедляется и температура достигает установившегося значения.

Это уравнение дает температуру проводника в любой момент времени t с начала прохождения тока.

Величина установившегося перегрева может быть получена, если в уравнении нагрева принять время t =∞

где vу — установившаяся температура поверхности проводника; Θу — установившееся значение превышения температуры проводника над температурой окружающей среды.

Рис. 1. Кривые нагрева и охлаждения электрооборудования: а — изменение температуры однородного проводника при длительном нагреве; б — изменение температуры при охлаждении

На основании этого уравнения можно написать, что

Отсюда видно, что при достижении установившегося режима все выделяющееся в проводнике тепло будет отдаваться в окружающее пространство.

Вводя в основное уравнение нагрева Θу и обозначая через T =Gc/KF получим то же уравнение в более простом виде:

Величина T =Gc/KF называется постоянной времени нагрева и представляет собой отношение теплопоглощающей способности тела к его теплоотдающей способности. Она зависит от размеров, поверхности и свойств проводника или тела и не зависит от времени и температуры.

Для данного проводника или аппарата эта величина характеризует время достижения установившегося режима нагрева и принимается за масштаб измерения времени на диаграммах нагрева.

Хотя из уравнения нагрева следует, что установившийся режим наступает через неограниченно длительное время, на практике время достижения установившейся температуры принимают равным (3—4)•T, так как при этом температура нагрева превышает 98% своего окончательного значения Θу.

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Постоянную времени нагрева для простых токоведущих конструкций можно легко вычислить, а для аппаратов и машин она определяется путем тепловых испытаний и последующих графических построений. Постоянная времени нагрева определяется как подкасательная ОТ, построенная по кривой нагрева, а сама касательная ОВ к кривой (от начала координат) характеризует подъем температуры проводника при отсутствии теплоотдачи.

При больших плотностях тока и интенсивном нагревании постоянную времени нагрева рассчитывают по уточненному выражению:

Если предположить, что процесс нагрева проводника происходит без отдачи тепла в окружающее пространство, то уравнение нагрева будет иметь следующий вид:

и температура перегрева будет нарастать по линейному закону, пропорционально времени:

Если в последнее уравнение подставить t =T, то видно, что за период, равный постоянной времени нагрева T =Gc/KF проводник нагревается до установившейся температуры Θу=I2Ra/KF, если за это время не будет происходить теплоотдача.

Величина постоянной времени нагрева для электрического оборудования колеблется от нескольких минут у шин до нескольких часов у мощных трансформаторов и генераторов.

В табл. 1 приводятся значения постоянных времени нагрева для шин некоторых типовых размеров.

При отключении тока прекращается подвод энергии к проводнику, т. е. Pdt=0, поэтому, начиная с момента выключения тока, проводник будет охлаждаться.

Основное уравнение нагрева для этого случая следующее:

Таблица 1. Постоянные времени нагрева медных и алюминиевых шин

Нагрев электрических аппаратов

Источники тепловой энергии в электрических аппаратах:

1) Нагрев проводников с током, обычно он называется нагревом методом электрического сопротивления.

W_Q = I 2 _* R _* t — закон Джоуля — Ленца.

Закон Джоуля — Ленца гласит, что в любом теле, обладающем электрическим сопротивлением, выделяется тепловая энергия пропорциональная квадрату тока, сопротивления электрического тела и времени протекания тока.

На постоянном токе — R₌ = r _*

К_Д — Коэффициент добавочных потерь.

К_П -коэффициент поверхностного эффекта

К_Б — коэффициент близости.

Данная энергия идет на нагрев самого аппарата (токоведущих частей), нагрев прилегающих материалов и нагрев окружающей среды по законам теплопередачи (теплопроводности, конвекции и теплового излучения).

2) Энергия, выделяющаяся в деталях их ферромагнитных материалов (в нетоковедущих частях):

2.1. Магнитопроводы, предназначенные для усиления магнитного поля, создаваемого проводником с током.

Причина нагрева:

а) Потери от вихревых токов

Рассмотрим элемент магнитопровода.

Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

При прохождении переменного магнитного потока по магнитопроводу в нем появляется ЭДС согласно закону электромагнитной индукции:

e =

Под действием этой ЭДС появляется ток, который называется вихревым, такого направления при котором создаваемые им магнитные потоки противодействуют изменению основного магнитного потока (правило Ленца).

При протекании вихревых токов по магнитопроводу, согласно закону Джоуля – Ленца, происходит преобразование электрической энергии в тепловую.

Для уменьшения потерь данного вида, магнитопроводы выполняются шихтованными из пластин электротехнической стали толщиной 0,2 ¸ 0,5 мм, тщательно изолированных друг от друга. Этим самым исключается контур протекания вихревого тока.

б) Потери на гистерезис — это энергия, затраченная на поворот доменов.

Полные потери в магнитопроводе вычисляются по формуле:

P_Ж =

P_Ж — мощность железа

K_T = 1,9 ¸ 2,6 — коэффициент потерь на гистерезис ;

K_В = 0,4 ¸ 1,2 — коэффициент потерь на вихревые токи;

f — частота сети;

Bm — амплитуда вектора магнитной индукции;

G_T — масса магнитопровода [кг].

2.2. Потери в конструкциях аппарата.

Выделение потерь в стальных элементах конструкции происходит аналогично, что и в магнитопроводе.

Для снижения потерь используются следующие мероприятия:

а) Введение немагнитных зазоров на пути магнитного потока.

б) За счет надевания на стальные конструкции короткозамкнутого витка с малым активным сопротивлением. При этом в нем индуцируется ЭДС, протекает ток, от которого возникают магнитные потоки, направленные встречно основному.

в)При токах выше 1000 А не должно быть стальных деталей, а все детали должны быть изготовлены из немагнитных материалов (алюминий, бронза, немагнитные чугуны, пластмассы).

3)Выделение энергии в диэлектрике.

Изоляция моделируется следующей схемой замещения:

С — ёмкость изоляции; tg(d) = 0,005 ¸ 0,0001

При появлении дефектов в отдельных местах изоляции возникают местные тепловые выделения, которые способны вызвать тепловой пробой изоляции (изоляция обугливается и становится проводящей).

4) Другие виды источников теплоты в электрических аппаратах:

4.1. Энергия выделяемая в электрических дугах.

Видео:ИЗИ Физика. Уравнение теплового баланса. Фазовые переходыСкачать

4.2. При трении между собой отдельных элементов электрических аппаратов.

Нагрев электрических аппаратов вызывает ускоренное старение изоляции и повышает скорость окисления электрических контактов, что в конечном итоге снижает срок службы электрического аппарата.

Уравнение теплового баланса при нагреве однородного проводника во времени при продолжительном режиме работы.

Тепловая энергия, выделяемая в проводнике с током может быть разделена на две составляющие:

1.Нагрев самого проводника

2.Нагрев окружающей среды.

Уравнение теплового баланса в дифференциальной форме:

(*)

С — удельная теплоемкость [Дж/кг´град]

G — масса проводника [кг]

F — поверхность проводника, т.е. поверхность теплоотдачи [м 2 ]

Кт — коэффициент теплоотдачи [Вт/м 2 ´град]

Коэффициент теплоотдачи определяет то количество теплоты, которое отдается за 1с всеми видами теплопередачи с 1 м 2 теплоотдающей поверхности при разности температуры нагретого тела и окружающего пространства в 1°С

Кт = 10 ¸ 16 на воздухе

Кт = 25 ¸ 100 в масле.

t — это превышение температуры проводника над температурой окружающей среды. Эта величина является переменной (различна для каждого момента времени при нагреве).

dt — приращение данного превышения за время dt.

Разделим каждый член уравнения ( * ) на C ´ G ´ dt

t₀ — превышение температуры проводника над температурой окружающей среды в начале процесса нагрева при t = 0.

t_У — установившееся превышение температуры. Ищется из уравнения теплового баланса, поскольку в установившемся режиме dt = 0. Тогда:

T — постоянная времени нагрева

Т = [ c ]- это время, за которое нагревался бы проводник до значения Q_УСТ (установившееся температура), если бы отдачи тепла в окружающую среду не было.

Уравнение теплового баланса электрического аппарата

В установившемся режиме все выделяемое тепло отдается в окружающую среду. В обоих случаях нагрева нагрев до установившейся температуры происходит за одно и то же время, изменяется лишь скорость нагрева.

Т — всегда может быть рассчитана.

Если время нагрева не превышает 0.1*T (t_нагр. -t/T

При t_O = t_y кривая охлаждения является зеркальным отображением кривой нагревания.

Каждый электрический аппарат имеет какую-то свою допустимую температуру, т.е.

Q_ДОП — Q_ОПР.СР = t_у =

Видео:Уравнение теплового балансаСкачать

К_Т — коэффициент теплоотдачи

F — поверхность, с которой испускается тепло.

I_ДОП=

I_ДОП — ток, который допустимо пропускать по проводнику, кабелю, электрическому аппарату. При этом температура аппарата (кабеля, провода) не превышает допустимое значение. Такой ток называется длительно допустимым.

Для электрических аппаратов этот ток как правило называется номинальным, т.е. это ток, длительное протекание которого не вызывает нагрева электрического аппарата сверх допустимой температуры.