Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
- Что такое теплообмен и при каких условиях он происходит
- Уравнение теплового баланса и сохранение тепловой энергии
- Уравнение теплового баланса
- Если несколько тел участвуют в процессе теплообмена
- Пример расчетов для теплообмена между холодным и горячим телом
- Задача для самостоятельного решения:
- Химические процессы и реакторы (стр. 10 )
- § 6.1. Уравнение теплового баланса. Тепловые режимы химических реакторов
- § 6.2. Проточный реактор идеального смешения в неизотермическом режиме
- Тепловой баланс реактора
- 💡 Видео
Видео:ЕГЭ физика. Уравнение теплового баланса (термодинамика)Скачать

Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
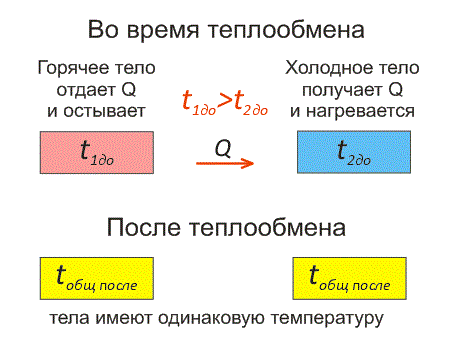
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
(large Q_<text> left( text right) ) – это количество теплоты горячее тело теряет.
(large Q_<text> left( text right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_ + Q_ = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed < Q_+ Q_ + Q_ + ldots + Q_ = 0 > ]
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
2). Теперь запишем формулу для каждого количества теплоты:
Примечания:
- (large c_<text> ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text> — t_<text> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text> — t_<text> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_<text> — 80 ) + 4200 cdot 0,1 cdot (t_<text> — 15 ) = 0 ]
[large 840 cdot (t_<text> — 80 ) + 420 cdot (t_<text> — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_ ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_ ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_ ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Видео:Урок 175. Уравнение теплового балансаСкачать

Химические процессы и реакторы (стр. 10 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Все тепловые явления учитываются при составлении теплового баланса химического реактора.
Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

§ 6.1. Уравнение теплового баланса.
Тепловые режимы химических реакторов
В уравнении теплового баланса учитываются все тепловые потоки, входящие в реактор и выходящие из него. Такими потоками являются: Q вых – физическая теплота реакционной смеси, входящей в элементарный объем, для которого составляется баланс (входной поток); Q вых – физическая теплота реакционной смеси, покидающей элементарный объем (выходной поток); Q xp – теплота химической реакции (знак теплового эффекта зависит от того, происходит ли выделение или поглощение теплоты в результате химической реакции); Q то – теплота, расходуемая на теплообмен с окружающей средой (в зависимости от соотношения температур в реакторе и окружающей среде или в теплообменном устройстве этот поток может быть также направлен и в объем и из него); Q фп – теплота фазовых превращений.
Для стационарного режима работы реактора алгебраическая сумма всех тепловых потоков равна нулю:
В нестационарном режиме происходит положительное или отрицательное накопление теплоты в элементарном объеме:
Q вх – Q вых ± Q хр ± Q то ± Q aп = Q нак . (6.2)
Уравнения (6.1) и (6.2) являются общими уравнениями теплового баланса химического реактора. Конкретный вид уравнения теплового баланса зависит от вида теплового режима и гидродинамической обстановки в реакторе. Различают несколько видов тепловых режимов химических реакторов. Рассмотрим различные тепловые режимы реакторов, в которых не происходит фазовых превращений.
В изотермическом режиме температура реакционной смеси, входящей в реактор, равна температуре в реакторе и температуре смеси, покидающей реактор. Это возможно, если выделение или поглощение теплоты в результате химической реакции полностью компенсируется теплообменом с окружающей средой. Для стационарного изотермического режима при постоянстве физических свойств системы можно записать:
Адиабатический режим характеризуется полным отсутствием теплообмена с окружающей средой. В этом случае вся теплота химической реакции полностью расходуется на нагрев или охлаждение реакционной смеси. Для стационарного адиабатического режима
Промежуточный режим характеризуется тем, что частично теплота химической реакции расходуется на изменение теплосодержания (нагрев или охлаждение) реакционной смеси, частично – на теплообмен с окружающей средой. Этот режим наиболее часто встречается в реальных химических реакторах. Промежуточный тепловой режим описывается полным уравнением теплового баланса (6.1).
В главе 5 были рассмотрены математические модели изотермических реакторов. Для расчетов на основе этих моделей, как правило, достаточно лишь уравнения материального баланса. При расчете неизотермического реактора необходимо совместно решить систему уравнений материального и теплового балансов, из которых первое учитывает изменение количества вещества, а второе – изменение количества теплоты при протекании химического процесса.
Ниже рассматриваются особенности составления математических моделей и расчетов на их основе для неизотермических реакторов с различной гидродинамической обстановкой.
Видео:Исследование уравнений теплового балансаСкачать

§ 6.2. Проточный реактор идеального смешения
в неизотермическом режиме
При составлении балансовых уравнений в качестве элементарного объема для реактора идеального смешения принимают полный реакционный объем V. Тепловые потоки за элементарный промежуток времени dτ для объема V:




где c p – средняя теплоемкость реакционной смеси; ρ – средняя плотность реакционной смеси; ∆H – тепловой эффект реакции, отнесенный к 1 моль реагента; К т – коэффициент теплопередачи; F то – поверхность теплообмена с окружающей средой; ∆Т то – движущая сила теплообмена (средняя разность температур в реакторе и внешней среде, с которой происходит теплообмен); величины, относящиеся к входному потоку, отмечены индексом «0», величины без индекса относятся к реакционной смеси, находящейся в реакторе в данный момент или выходящей из него.
Накопление теплоты в реакторе за время dτ равно изменению теплосодержания реакционной смеси:

С учетом уравнений (6.2)–(6.7) уравнение теплового баланса для нестационарного режима будет иметь вид

В стационарном режиме правая часть уравнения (6.8) равна нулю. Если также принять, что v 0 = v и пренебречь изменением средней теплоемкости и плотности реакционной смеси при изменении состава и температуры, для стационарного режима

Математическая модель неизотермического реактора идеального смешения кроме уравнения теплового баланса (6.9) включает в себя уравнение материального баланса

Уравнения (6.9) и (6.10) взаимосвязаны: в оба входит в качестве составной части функция w rA (c A , T). Скорость химической реакции w rA зависит и от концентрации реагентов (степени превращения), и от температуры. Чем выше температура, тем выше скорость реакции и, следовательно, тем большая степень превращения должна достигаться при том же среднем времени пребывания 
При совместном решении уравнений (6.9) и (6.10) при заданных

Совместное решение уравнений материального и теплового балансов для стационарного адиабатического реактора идеального смешения. Математическая модель проточного адиабатического реактора идеального смешения представляет собой систему уравнений материального и теплового балансов:

Определим, используя эту систему уравнений, степень превращения х А и температуру Т, достигаемые в реакторе. Различные частные решения зависят от конкретного вида кинетического уравнения w rA = w rA (c A , T) реакции, протекающей в аппарате. Рассмотрим решения для реакций с наиболее простой кинетикой: необратимой реакции первого порядка А

Предварительно преобразуем систему уравнений (6.11). В уравнении материального баланса заменим изменение концентраций (с А , 0 – c А ) равным ему соотношением с А , 0 х А . Упростим уравнение теплового баланса, исключив из него скорость реакции w rA .
Для этого воспользуемся уравнением материального баланса, в соответствии с которым w rA V = v(c A , 0 – с А ) = vc А ,0 x A . Тогда уравнение теплового баланса примет вид vc p ρ(Т 0 – Т) – ∆Hvс А , 0 х А = 0. После сделанных преобразований систему уравнений (6.11) запишем так:


Необратимая реакция первого порядка. Кинетическое уравнение необратимой реакции первого порядка имеет вид

Подставим его в уравнение (6.12)

Для определения степени превращения х А и температуры Т в реакторе уравнение материального баланса (6.14) нужно решить совместно с уравнением теплового баланса (6.13). Аналитическое решение этой системы уравнений затруднено из-за того, что температура T входит в уравнения и в виде линейного члена, и в составе комплекса, являющегося показателем экспоненциальной функции. Такие уравнения являются трансцендентными, и для их решения применяют численные методы.
Решим систему уравнений (6.13) и (6.14) графическим методом. Для этого запишем оба уравнения в виде зависимостей х А Т, построим графики этих зависимостей и найдем точки их пересечения, удовлетворяющие одновременно обоим уравнениям, т. е. являющиеся решениями системы.
В уравнении теплового баланса (8.14) зависимость между х А и T является линейной.
Эта прямая линия пересекает ось температур в точке Т = Т 0 и имеет угловой коэффициент

Знак углового коэффициента зависит от знака теплового эффекта, он отрицателен для эндотермических реакций, у которых ∆Н > 0 (рис. 6.1, а), и положителен для экзотермических реакций (рис. 6.1, б). Крутизну угла наклона можно изменить, меняя начальную концентрацию с A , 0 .
Рис. 6.1. Уравнение теплового баланса реактора идеального смешения
в координатах хА – Т для эндотермической (а) и экзотермической (б) реакций
Если принять х А = 1 (т. е. реакция прошла до конца), из уравнения (6.15) получим
Величина ∆TАД – максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях, или адиабатическое изменение температуры (для экзотермических реакций, например, адиабатический разогрев). Уравнение (6.15) с учетом ∆T ад можно записать так:

Вид зависимости х А (T), соответствующей уравнению материального баланса (6.12), зависит от типа кинетического уравнения реакции. Для необратимой реакции первого порядка (эндотермической, и экзотермической) уравнение материального баланса (6.12) можно представить в следующем виде (с учетом того, что V/v = ):

Уравнение (6.17) описывает монотонно возрастающую функцию х a ( T ). При низких температурах, когда кинетическая энергия молекул существенно ниже энергии активации (об этом можно судить, сравнивая энергии Е и RT), х А 

Таким образом, график функции (6.17) – кривая без экстремумов (рис. 6.2, кривая 1), при низких температурах асимптотически приближающаяся к нулю, при высоких – к единице, а при «средних» температурах имеющая одну точку перегиба (ее координаты можно получить, приравняв нулю производную d 2 x A /dT 2 ).
Положение среднего участка кривой относительно оси температур можно изменить, увеличив или уменьшив среднее время пребывания в реакторе ( = V/v). Из уравнения (6.17) следует, что увеличение при тех же температурах приведет к росту х А (рис. 6.2, кривая 2).
Рис. 6.2. Уравнение материального баланса реактора идеального смешения в координатах хA – Т для необратимой реакции первого порядка
при среднем времени пребывания 
Решение системы уравнений материального и теплового балансов имеет несколько различающийся вид для эндо — и экзотермических необратимых реакций. В случае проведения в адиабатическом реакторе идеального смешения необратимой эндотермической реакции графики функций (6.16) и (6.17) имеют лишь одну точку пересечения (см. рис. 6.3).
Координаты этой точки (х А / , T/) и являются решением системы уравнений: если в адиабатический реактор идеального смешения заданного объема V подает исходный реагент А, имеющий концентрацию с А , 0 с объемным расходом v и при начальной температуре Т 0 , необратимая эндотермическая реакция будет протекать в аппарате при температуре Т и при этом будет достигаться степень превращения х А / .
Рис. 6.3. Уравнения теплового (1) и материального (2) балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой эндотермической реакции (совместное решение)
Если в адиабатическом реакторе проводят необратимую экзотермическую реакцию, система уравнений материального и теплового балансов может иметь как одно, так и несколько решений, отвечающих стационарному режиму.
Из рис. 6.4 видно, что графики функций (6.16) и (6.17) имеют только одну точку пересечения, если начальная температура Т 0 реакционного потока будет сравнительно низкой (например, Т 10 ) или сравнительно высокой (например, T 20 ). При этом оказывается, что при подаче реагентов в реактор с низкой начальной температурой Т 10 процесс будет протекать при температуре, мало отличающейся от T 10 , а достигаемая степень превращения (ордината точки А на рис. 6.4) также будет очень низка. Более выгодным является режим работы реактора, соответствующий начальной температуре Т 30 . В этом случае также имеется лишь одна точка пересечения графиков (точка Е), т. е. одно решение системы уравнений, но оно соответствует высокой степени превращения, почти равной единице.
Если же реагенты подавать в реактор с начальной температурой Т 20 , то линии, соответствующие уравнениям материального и теплового балансов, пересекаются трижды, т. е. координаты точек В, С, D являются возможными решениями системы уравнений, составляющей математическую модель адиабатического реактора идеального смешения.
В таких случаях говорят о множественности стационарных состояний реактора. При этом возникает дополнительная проблема устойчивости рассматриваемых стационарных состояний.
Рис. 6.4. Уравнения теплового (1, 2, 3) и материального (4) балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой экзотермической реакции (совместное решение)
Обратимая реакция первого порядка. Для обратимой реакции первого порядка А 

Выразив в уравнении (6.18) концентрации с А и с R через с А , 0 и х А получим
В условиях равновесия для обратимой реакции первого порядка имеет место равенство скоростей прямой и обратной реакции 
С учетом выражения (6.19) кинетическое уравнение обратимой реакции первого порядка примет вид

После подстановки выражения (6.20) в формулу (6.12) уравнение материального баланса можно представить в виде зависимости х А от Т:

Уравнение (6.21), как и следовало ожидать, при х А , е = 1 (т. е. для необратимой реакции первого порядка) переходит в уравнение (6.17).
Для графического решения системы уравнений материального и теплового балансов в случае обратимой реакции нужно построить график функции (6.21). График уравнения теплового баланса (6.15), не содержащего никаких кинетических параметров реакции, от вида кинетического уравнения не зависит.
В уравнении (6.21) от температуры зависят константа скорости прямой реакции k 1 , и равновесная степень превращения х А , е .
Для обратимой эндотермической реакции (∆H > 0) с ростом температуры увеличивается и константа равновесия, и равновесная степень превращения. Величина х А , рассчитанная по уравнению (6.21), при любых температурах будет меньше, чем k 1 , , и меньше, чем х А , е , т. е. грфик функции х А (Т) должен находиться на координатной плоскости (рис. 6.5, a) ниже графиков функций k 1 (Т) и х А ,e (Т).
Система уравнений материального и теплового балансов для обратимой экзотермической реакции имеет такой же вид, как и для обратимой эндотермической реакции, т. е. это уравнения (6.21) и (6.15). Однако график функции х А (Т), определяемый уравнением (6.21), будет другим. Связано это с тем, что равновесная степень превращения х А , е для экзотермических реакций с ростом температуры падает. Поэтому, построив график функции х А (Т), пользуясь при этом теми же приемами, что и для обратимой экзотермической реакции, получим кривую с максимумом (рис. 6.5, б). Абсолютное значение максимума и его положение относительно кривой определяются, с одной стороны, средним временем пребывания реагентов в реакторе τ, а с другой – состоянием химического равновесия.
Уравнение теплового баланса – прямая 1 с положительным тангенсом угла наклона. Эта прямая может пересекаться с кривой 2, отвечающей уравнению материального баланса, в одной или в нескольких точках (одно или несколько стационарных состояний).
Рис. 6.5. Уравнения теплового (1) и материального (2) балансов
для адиабатического реактора идеального смешения при проведении
в нем обратимых эндотермической (а) и экзотермической (б) реакций
(совместное решение)
Способы увеличения степени превращения реагентов при проведении реакций в адиабатическом реакторе идеального смешения. В зависимости от начальных условий (температуры на входе Т 0 , начальной концентрации с А , 0 ), соотношения объема аппарата и объемного расхода ( = V/v), а также типа химической реакции в проточном реакторе идеального смешения устанавливается некоторое стационарное состояние, характеризующееся неизменяющимися во времени значениями температуры реакционной смеси и степени превращения на выходе из аппарата. Эти значения T и x A могут быть определены на основании совместного решения уравнений материального и теплового балансов, как это было показано выше.
В промышленных условиях очень важно наиболее полно использовать исходное сырье, т. е. достичь высоких значений степени превращения. Анализ получающихся решений позволяет найти условия проведения процесса, при которых достигается оптимальная степень превращения реагентов в адиабатическом реакторе идеального смешения.
Графическое решение системы уравнений материального и теплового балансов сводится к определению точки пересечения графиков функций х А (Т), отвечающих и тому, и другому уравнениям. Более высокая степень превращения исходного сырья в адиабатическом реакторе соответствует на рис. 6.3–6.5 смещению точки пересечения в область больших значений х А . Добиться этого можно, изменяя взаимное положение кривой, отвечающей уравнению материального баланса, и прямой, соответствующей уравнению теплового баланса. Укажем возможные способы влияния на положение этих линий.
Для эндотермических реакций (необратимых и обратимых) повышения степени превращения можно добиться, прежде всего, увеличением начальной температуры T 0 , что приведет к параллельному смещению вправо прямой 1 (см. рис. 6.3 и 6.5, а).
Для необратимых экзотермических реакций увеличение температуры на входе в реактор также приведет к росту степени превращения (см. рис. 6.4, прямая 2). Одновременно это позволит избежать тройного пересечения линий 2 и 4, отвечающего случаю множественности стационарных состояний. Однако увеличение начальной температуры должно быть оправдано экономическими соображениями, так как рост степени превращения будет сопровождаться при этом и увеличением затрат на нагрев исходной реакционной смеси.
Для обратимых экзотермических реакций, проводимых в адиабатическом реакторе идеального смешения, целесообразно добиться таких условий, чтобы решение системы уравнений материального и теплового балансов соответствовало точке максимума линии 2, отвечающего уравнению материального баланса (см. рис. 6.5, б). Смещение прямой 1 вправо при возрастании начальной температуры может привести не к увеличению, а к уменьшению степени превращения. Выбор оптимальных условий проведения обратимых экзотермических реакций представляет наибольшую сложность.
Другой способ изменения положения прямой, отвечающей уравнению теплового баланса, состоит в изменении угла ее наклона. Угловой коэффициент прямой, описываемой уравнением (6.15), можно увеличить или уменьшить, изменив начальную концентрацию с А , 0 :

В эндотермических реакциях для повышения х A при сохранении прежней начальной температуры нужно увеличить крутизну прямой, что можно сделать уменьшением с A , 0 (это не всегда целесообразно, так как придется работать с низко концентрированными реагентами). При проведении экзотермических реакций увеличение с А , 0 приведет к росту ∆Т ад , и прямая станет более пологой.
Видео:Уравнение теплового балансаСкачать

Тепловой баланс реактора
Энергетический (тепловой) баланс любого аппарата может быть представлен в виде уравнения, связывающего приход и расход энергии процесса. Энергетический баланс составляется на основе закона сохранения энергии, в соответствии с которым в замкнутой системе сумма всех видов энергии постоянна. Обычно для химико-технологических процессов составляется тепловой баланс. Для аппаратов непрерывного действия тепловой баланс составляют на единицу времени, а для аппаратов периодического действия — на время цикла обработки.
Применительно к тепловому балансу закон сохранения энергии формулируется следующим образом: приход теплоты в данном аппарате должен быть равен расходу теплоты в том же аппарате.
т.е. тепловые потоки, увеличивающие количество тепла внутри системы, берутся со знаком плюс и относятся к статьям прихода. Соответственно тепловые потоки, которые уменьшают количество тепла внутри системы, относятся к статьям расхода. При составлении теплового баланса учитывается теплота, поступающая с потоком исходного сырья Q01; теплота химической реакции Qх.р; теплота подводимая или отводимая с помощью теплообменных устройств Qт.о; теплота, уходящая с потоком продуктов Q02; теплота фазовых переходов Qф.п; потери тепла в окружающую среду Qп; положительное или отрицательное накопление теплоты в объеме аппарата Qнак.
Для стационарного режима работы аппарата Qнак равно нулю, т.е. уравнение теплового баланса можно записать следующим образом:
Теплоту, поступающую с потоком сырья и уходящую с потоком продуктов, рассчитывают следующим образом:
где N01, N02 – суммарные мольные потоки на входе и выходе из реактора (кмоль/ч);
Ср1, Ср2 – средняя мольная теплоемкость смеси на входе и выходе из реактора (кДж/(кмоль·К); Т1, Т2 – температура смеси на входе и выходе из реактора (К).
Среднюю теплоемкость для реакции (3.2) можно рассчитать по уравнениям:
СрА, СрB, СрC, СрD, СрI – мольные теплоемкости веществ, приведены в справочниках термодинамических величин.
Из расчета материального баланса Q01 и Q02 можно также определить, используя мольные потоки компонентов смеси:
Теплота химической реакции определяется по формуле:
где ΔН (кДж/кмоль) – изменение энтальпии реакции, численно равное тепловому эффекту реакции, взятому с обратным знаком. ΔН находят как разность энтальпии продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов:
Значения энтальпии образования веществ, приведены в справочниках термодинамических величин.
Потери тепла в окружающую среду определяются обычно в процентах от теплоты прихода.
При решении задач, с целью упрощения расчетов, теплоемкость и энтальпия образования веществ берутся из справочника при 298 К.
Пример расчета материального и теплового баланса
Составить материальный баланс колонны синтеза аммиака, если известно, что в исходной смеси концентрация водорода составляет 60 % (об.), азота 18 %(об.), аммиака 3 %(об.) (смесь циркулирует по замкнутому контуру и поэтому в исходной смеси присутствует продукт реакции аммиак). Кроме того, известно, что в конечной смеси концентрация аммиака составляет 18 %(об.), расход конечной смеси при нормальных условиях 50000 м 3 /ч. В смесях присутствует инертное вещество — метан. Дополнительно рассчитать степень превращения водорода.
Рассчитать количество теплоты, которое необходимо отвести из реактора, чтобы температура на выходе составляла 600 0 С. Температура входной смеси 400 0 С, потери тепла в окружающую среду составляют 3% от теплоты, поступающей с потоком исходных веществ.
Составим уравнение реакции в обычном виде, с учетом стехиометрических коэффициентов. Определим количество веществ, которые надо принять в расчет (включая инертное) и кратко обозначим их латинскими буквами. Определим их молекулярные массы, используя таблицу Д.И.Менделеева. Объемные (мольные) проценты веществ переведем в доли единицы (разделив на 100%) и запишем исходные данные:
Целью расчета материального баланса является определение количества молей, массы, объема и мольных долей всех веществ в начальной и конечной смеси. Для этого необходимо выразить все неизвестные через известные величины. Так как в условии задачи больше данных об аммиаке, обозначим за Y количество молей NH3, которое образовалось в ходе реакции (ΔNC), и запишем приращения остальных веществ через соотношения (4.1.12), используя величину Y.
Составим балансовые уравнения по каждому веществу и суммарное уравнение мольных потоков:
Преобразуем уравнение (III), выразив количество молей аммиака в начальной и конечной смеси через мольную (объемную долю) и суммарные мольные потоки.
из уравнения (VI) следует
подставим (VIII) в (VII) и выразим Y:
Рассчитаем Y, подставив исходные данные:
Y = 50000/22,4∙(0,18 – 0,03)/( 0,03 + 1) = 325,069 кмоль/ч.
Определим суммарный мольный поток исходной смеси по уравнению (VIII)
N01 = 50000/22,4 + 325,069 = 2557,212 кмоль/ч.
Количество молей каждого вещества в исходной смеси:
Количество инертного вещества можно рассчитать по уравнению
Количество веществ в конечной смеси рассчитывают из уравнений (I- IV), соответственно:
NВ2 = NВ1 – 1/2∙Y = 460,298 — 1/2∙325,069 = 297,764 кмоль/ч;
NС2 = NС1 + Y = 76,716 + 325,069 = 401,785 кмоль/ч;
для проверки правильности расчета определим количество инерта в конечной смеси по формуле:
Таким образом, известны количества всех веществ в начальной и конечной смеси (кмоль/ч), теперь рассчитаем массы, объемы и мольные доли используя формулы (4.1.1 – 4.1.3).
Результаты расчетов удобно представить в виде таблицы:
| Приход | Расход | |||||||
| Вещества | N (кмоль/ч) | G, (кг/ч) | V, (м 3 /ч) | Z, доля мольная | N (кмоль/ч) | G, (кг/ч) | V, (м 3 /ч) | Z, доля мольная |
| H2 (A) | 1534,327 | 3068,654 | 34368,925 | 0,6 | 1046,723 | 2093,447 | 23446,595 | 0,467 |
| N2 (B) | 460,298 | 12888,344 | 10310,675 | 0,18 | 297,764 | 8337,392 | 6669,914 | 0,133 |
| NH3 (C) | 76,716 | 1304,172 | 1718,4384 | 0,03 | 401,785 | 6830,345 | 8999,984 | 0,18 |
| CH4 (I) | 485,871 | 7773,936 | 10883,510 | 0,19 | 485,870 | 7773,92 | 10883,488 | 0,219 |
| ИТОГО: | 2557,212 | 25035,106 | 57281,549 | 2232,143 | 25035,104 |
Степень превращения водорода рассчитывают по формуле (3.4):

Для расчета теплового баланса найдем в справочнике теплоемкости и энтальпии образования всех компонентов смеси (при 298 0 С).
| Вещества | Ср при 298 0 С Дж/(моль∙К) | ΔН при 298 0 С кДж/моль |
| H2 (A) | 28,93 | |
| N2 (B) | 29,10 | |
| NH3 (C) | 35,65 | -46,19 |
| CH4 (I) | 35,79 | — |
Определим теплоту, поступающую с потоком сырья по формуле (4.2.7), для этого рассчитаем количество теплоты, вносимое каждым компонентом:
Чтобы соблюсти размерности, кмоли переводим в моли, а температуру записываем в Кельвинах (t 0 С+273).
Q01 = 298,7·10 8 + 90,1·10 8 +18,4·10 8 +117,0·10 8 = 524,2 ·10 8 Дж/ч.
Рассчитаем теплоту потерь:
Qп =0,03· Q01 = 0,03· 524,2 ·10 8 = 15,726·10 8 Дж/ч.
Определим теплоту химической реакции по формуле(4.2.11), для этого рассчитаем изменение энтальпии:
ΔН = -46,19 -0 -0 = -46,19 кДж/моль = -46,19·10 3 Дж/моль.
Т.к. ΔН имеет знак минус, то реакция экзотермическая, идет с выделением тепла.
Qх.р = 46,19·10 3 ·(401,785 — 76,716) ·10 3 = 150,2·10 8 Дж/ч.
Определим теплоту, уходящую с потоком продуктов по формуле (4.2.9), для этого рассчитаем количество теплоты, уносимое каждым компонентом:
Q02 = 264,4·10 8 + 75,6·10 8 +125·10 8 +151,8·10 8 = 616,8 ·10 8 Дж/ч.
Общее уравнение теплового баланса для стационарного режима (все реагирующие вещества – газы, поэтому нет теплоты фазовых переходов):
Qто =524,2 ·10 8 + 150,2·10 8 — 616,8 ·10 8 — 15,726·10 8 = 41,874 ·10 8 Дж/ч.
💡 Видео
Урок 127 (осн). Задачи на уравнение теплового баланса - 1Скачать

Урок 128 (осн). Задачи на уравнение теплового баланса - 2Скачать

🔴 ЕГЭ-2022 по физике. Уравнение теплового балансаСкачать

89 НЕ ЗНАЮТ этого в Физике: Что такое Количество Теплоты, Теплоемкость, Уравнение Теплового БалансаСкачать

10 класс, 11 урок, Уравнение теплового баланса с учетом изменения агрегатного состояния веществаСкачать

Формы записи уравнения теплового балансаСкачать

C-шки по физике #3 Уравнение теплового балансаСкачать

Задача на Тепловой обмен. физика 8 классСкачать

Физика. Объяснение темы "Закон сохранения внутренней энергии и уравнение теплового баланса"Скачать

❗ Количество теплоты ❗ Уравнение теплового баланса + РЕШЕНИЕ задачСкачать

Теплообмен. Уравнение теплового баланса 8-10 класс | Физика TutorOnlineСкачать

Уравнение теплового баланса, термодинамика в изопроцессах | Физика ЕГЭ 10 класс | УмскулСкачать

Урок 176. Задачи на уравнение теплового балансаСкачать