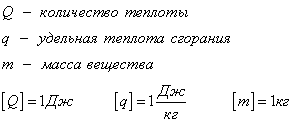Уравнение теплового баланса для конденсации (4 видео)

Содержание

Уравнение теплового баланса
Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)
Плавление или кристаллизация
Кипение или конденсация
Уравнение теплового баланса для конденсации
Испарение
Конденсация
🎦 Видео

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Уравнение теплового баланса

Нагревание и охлаждение

Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле

Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К=1 0 С. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость — табличная величина.

Теплоемкость вещества (тела) С — это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К.

При вычислении ΔT договоримся из большей температуры вычитать меньшую. Тогда количество теплоты будет всегда положительной величиной. Это уменьшает вероятность ошибки при сложении количества теплоты, выделяющегося при охлаждении с количеством теплоты выделяющимся, например, при кристаллизации.

Горение

Количество теплоты, которое выделяется при сгорании вещества

Удельная теплота сгорания табличная величина.

Плавление и кристаллизация

Плавление — переход вещества из твердого состояния в жидкое. Обратный переход называется кристаллизацией.

Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле

Значение удельной теплоты плавления можно найти в таблицах.

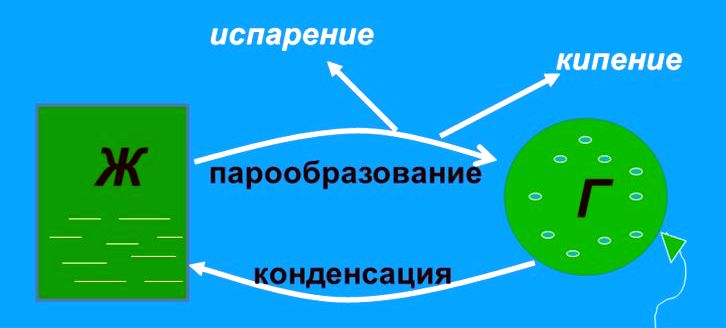
Парообразование (испарение или кипение) и конденсация

Парообразование — это переход вещества из жидкого (твердого) состояния в газообразное. Обратный процесс называется конденсацией.

Удельная теплота парообразования табличная величина.

Уравнение теплового баланса

Если мы рассмотрим изолированную (нет обмена энергией с окружающей средой) систему тел (твердых или жидких), в которой теплообмен может совершаться только между телами входящими в эту систему, то в результате этого процесса в системе установится тепловое равновесие. Температуры всех тел станут одинаковыми и равными некоторому значению Q.

В процессе теплообмена тела, начальные температуры которых больше Q («горячие» тела), будут отдавать свою энергию, а тела, у которых начальные температуры меньше Q, — получать энергию.

Из закона сохранения энергии (т.к. система изолированная) следует, что количество теплоты, потерянное телами с более высокой температурой, будет равно количеству теплоты, приобретенному телами с более низкими температурами.

Q_отд=Q_получ где Q_отд — количество теплоты, отданное «горячими» телами; Q_получ — количество теплоты, полученное «холодными» телами.

Это уравнение носит название уравнения теплового баланса. А положение, что количество теплоты, потерянное «горячими» телами, равно количеству теплоты, приобретенному «холодными телами» называется законом теплообмена.

В приведенном выше подходе при составлении уравнения теплового баланса мы везде из большего значения температуры должны вычитать меньшее, тогда значения количеств теплоты всегда были положительными.

«Виртуальный банк» тепла

Довольно часто встречаются задачи в которых требуется найти конечную температуру системы. Хорошо, если из контекста понятно в каких агрегатных состояниях будут находиться вещества после прекращения теплообмена. Тогда уравнение теплового баланса удается записать с первого раза. Но если непонятно что получится в конце (например, вода, смесь вода+лед, смесь вода+пар и т.п.) то приходится либо по очереди перебирать все варианты, находить конечную температуру и смотреть не противоречит ли она равновесному состоянию данной системы (к примеру, смесь вода+лед не будет существовать при +15 0 С), либо поэтапно сравнивать отдельные количества теплоты и все время отвечать на вопросы… «хватит — не хватит?».

Но есть и другой подход, основанный на замечательном свойстве закона сохранения энергии – связывать начальные и конечные состояния системы независимо от процесса перехода. Если система сложно шла к установлению теплового равновесия, то всегда можно представить весь переход в виде набора из нескольких элементарных процессов, расчет которых не вызывает труда. Пусть даже эти элементарные процессы заведомо не могут протекать в реальной жизни. Окончательный результат (в данном случае, конечная температура) все равно окажется такой же, как и в случае одного сложного процесса.

Поясним на примере. Пусть произошла разгерметизация кастрюли-скороварки с перегретой водой. Масса воды в кастрюле m. Начальная температура T (T>T_{кипения}). Какая часть воды испарится?

Сколько тепла забирает/отдает перегретая вода не совсем ясно, зато мы умеем рассчитывать, сколько выделит эта вода при остывании и сколько тепла потребуется для испарения некоторой массы при температуре кипения. Тогда предложим схему некоторого виртуального банка тепла. Предположим, что вся перегретая вода остынет до температуры кипения. Тогда она выделит некоторое Q₁=mc(T-T_{кипения}). Временно «отправим» это тепло в банк. Теперь найдем сколько потребуется тепла для испарения некоторой массы m_п при температуре кипения? Это легко Q₂=m_пL. Если система теплоизолирована, то тепло на испарение мы можем взять только из виртуального банка. Q₁=Q₂. Окончательно . Такой прием особенно выгодно применять в случае теплообмена большого количества тел (и нагревателей), для процессов со сложной и непонятной физикой теплообмена и для поиска конечной температуры системы.

В последнем случае, можно мысленно охладить всю систему до температуры самого холодного тела. Посчитать выделившееся при этом тепло и пустить его на нагревание сразу всей системы.

Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)

Разделы: Физика

Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.

При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При “столкновениях” молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).

Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. (Здесь и в дальнейшем единицы измеряются в системе СИ.)

Нагревание или охлаждение

При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:

(t₂ – t₁) – разность температур тела,° С (или К);

с – удельная теплоёмкость вещества, из которого состоит тело,

Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1° С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1° С).

Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.

При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.

При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.

Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой (тэта).

В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:

Размерность теплоемкости: Теплоемкость тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть его на 1° С (или сколько энергии выделяет это тело, остывая на 1° С).

Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0° С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.

Плавление или кристаллизация

Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

(3)

где m – масса тела, кг;

– удельная теплота плавления,

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину и эта теплота данным телом выделяется. Она поглощается другими телами, участвующими в теплообмене.

Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).

Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же

Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда t_пл = 0° С.

Кипение или конденсация

При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:

где m – масса тела, кг; L – удельная теплота парообразования,

Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).

При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.

Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: рис. 9 (при нормальном атмосферном давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.

Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.

При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t₂ следует брать большую температуру, а в качестве t₁ – меньшую. Тогда разность (t₂ – t₁) будет положительна и всё произведение cm(t₂–t₁) также будет положительным. Все теплоты, отданные и полученные, будут положительными.

Уравнение теплового баланса можно записать и в таком виде:

где n – количество тел системы.

Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.

Q₁, Q₂, …, Q_n – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t₂ – конечная температура, а t₁ – начальная.

Если тело нагревается, то разность (t₂ – t₁) положительна и все произведение cm(t₂ – t₁) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.

А если t₂ 0; если тело выделяет энергию (кристаллизация, конденсация), то Q

	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t₁ = t₂ = 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q₃.
Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q₁ и Q₂, которую они поглощают.
Решим задачу с использованием уравнения теплового баланса в виде (5):

Решим задачу с использованием уравнения теплового баланса в виде (6):

Ответ: Вода нагреется до 24° С.

Предлагаю читателю самостоятельно сделать проверку размерности.

Видео:Урок 175. Уравнение теплового балансаСкачать

Уравнение теплового баланса для конденсации

Явление превращения вещества из жидкого состояния в газообразное называется парообразованием. Парообразование может осуществляться в виде двух процессов: испарение и кипение.

Испарение

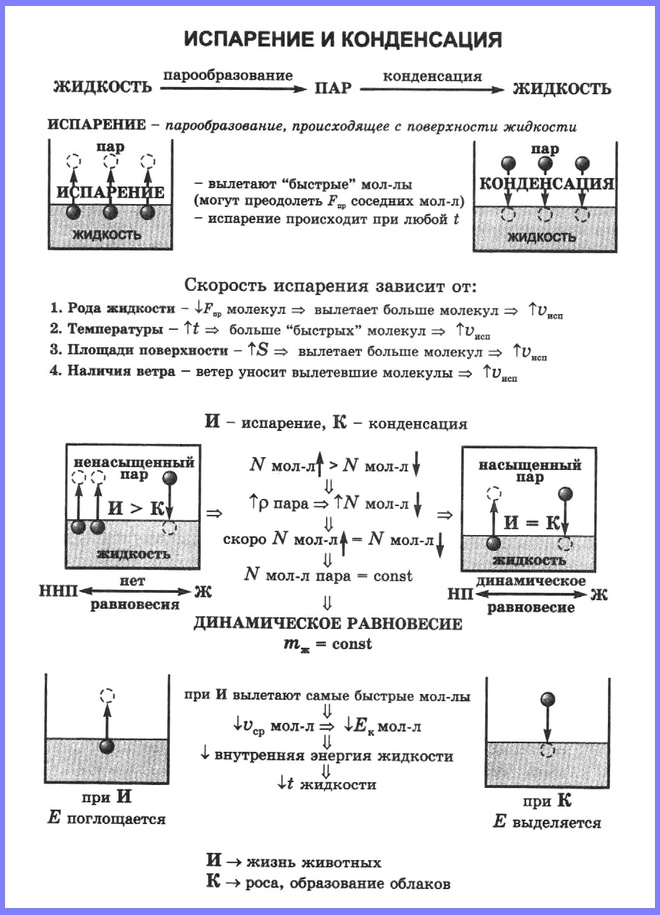
Испарение происходит с поверхности жидкости при любой температуре. Так, лужи высыхают и при 10 °С, и при 20 °С, и при 30 °С. Таким образом, испарением называется процесс превращения вещества из жидкого состояния в газообразное, происходящий с поверхности жидкости при любой температуре.

С точки зрения молекулярно-кинетической теории строения вещества испарение жидкости объясняется следующим образом. Молекулы жидкости, участвуя в непрерывном движении, имеют разные скорости. Наиболее быстрые молекулы, находящиеся на границе поверхности воды и воздуха и имеющие сравнительно большую энергию, преодолевают притяжение соседних молекул и покидают жидкость. Таким образом, над жидкостью образуется пар.

Поскольку из жидкости при испарении вылетают молекулы, обладающие большей внутренней энергией по сравнению с энергией молекул, остающихся в жидкости, то средняя скорость и средняя кинетическая энергия молекул жидкости уменьшаются и, следовательно, температура жидкости уменьшается.

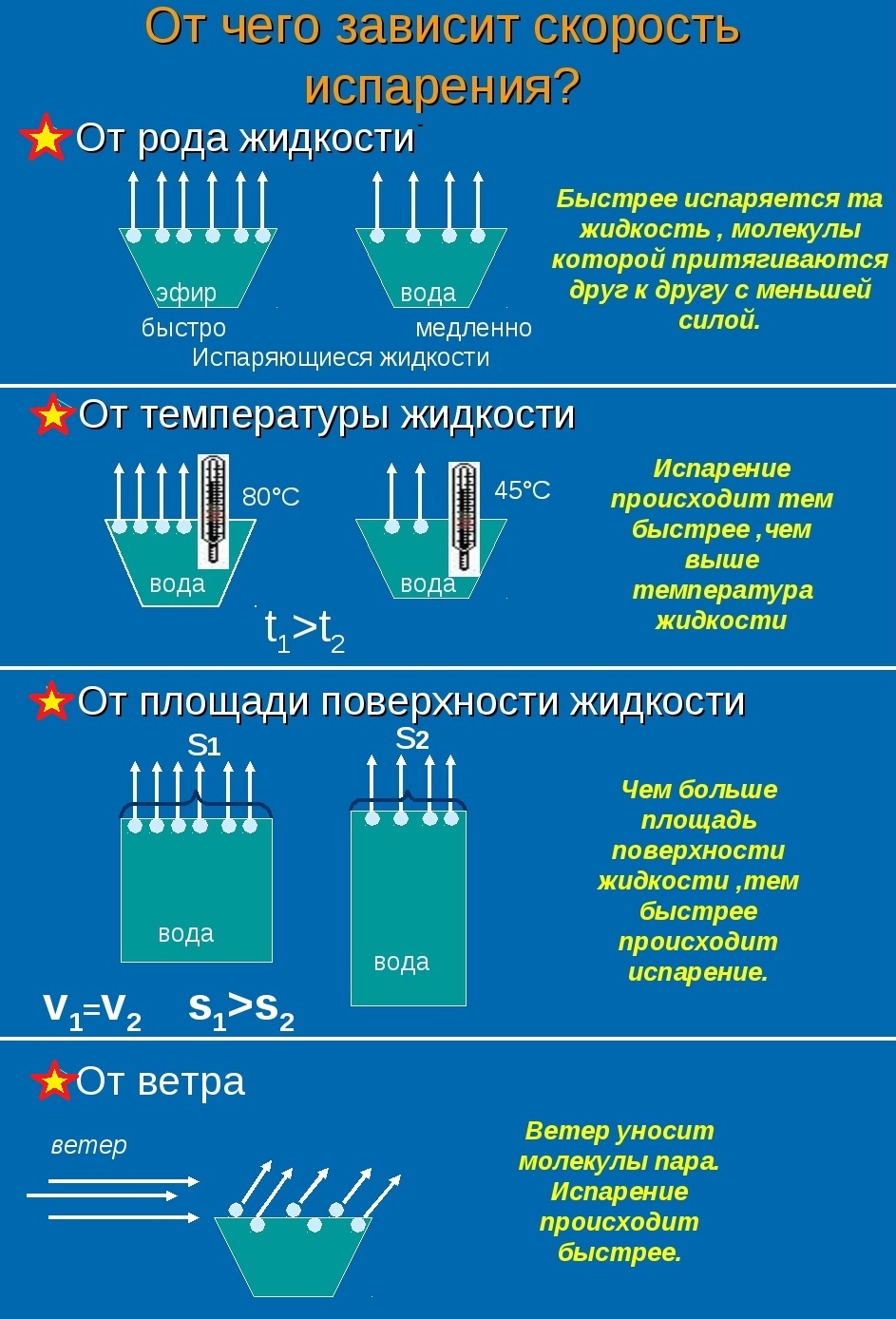
Скорость испарения жидкости зависит от рода жидкости. Так, скорость испарения эфира больше, чем скорость испарения воды и растительного масла. Кроме того, скорость испарения зависит от движения воздуха над поверхностью жидкости. Доказательством может служить то, что бельё сохнет быстрее на ветру, чем в безветренном месте при тех же внешних условиях.

Скорость испарения зависит от температуры жидкости. Например, вода при температуре 30 °С испаряется быстрее, чем вода при 10 °С.

Хорошо известно, что вода, налитая в блюдце, испариться быстрее, чем вода такой же массы, налитая в стакан. Следовательно, скорость испарения зависит от площади поверхности жидкости.

Конденсация

Процесс превращения вещества из газообразного состояния в жидкое называется конденсацией.

Процесс конденсации происходит одновременно с процессом испарения. Молекулы, вылетевшие из жидкости и находящиеся над её поверхностью, участвуют в хаотическом движении. Они сталкиваются с другими молекулами, и в какой-то момент времени их скорости могут быть направлены к поверхности жидкости, и молекулы вернутся в неё.

Если сосуд открыт, то процесс испарения происходит быстрее, чем конденсация, и масса жидкости в сосуде уменьшается. Пар, образующийся над жидкостью, называется ненасыщенным.

Если жидкость находится в закрытом сосуде, то вначале число молекул, вылетающих из жидкости, будет больше, чем число молекул, возвращающихся в неё, но с течением времени плотность пара над жидкостью возрастет настолько, что число молекул, покидающих жидкость, станет равным числу молекул, возвращающихся в неё. В этом случае наступает динамическое равновесие жидкости с её паром.

Пар, находящийся в состоянии динамического равновесия со своей жидкостью, называется насыщенным паром.

Если сосуд с жидкостью, в котором находится насыщенный пар, нагреть, то вначале число молекул, вылетающих из жидкости, увеличится и будет больше, чем число молекул, возвращающихся в неё. С течением времени равновесие восстановится, но плотность пара над жидкостью и соответственно его давление увеличатся.