Уравнение теплоты для изобарного процесса

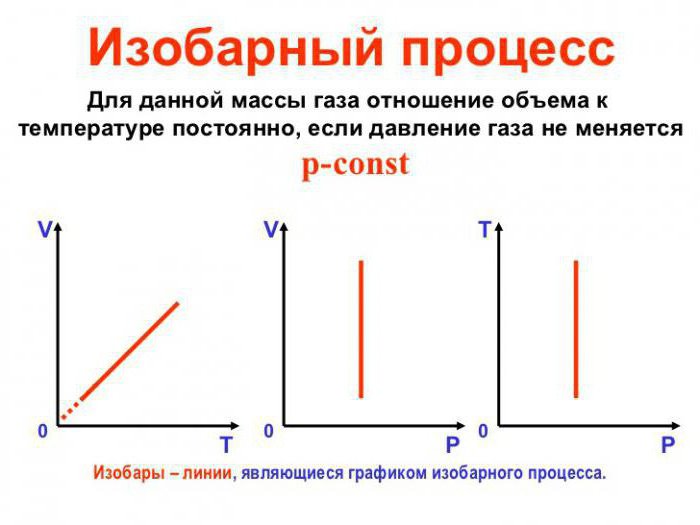
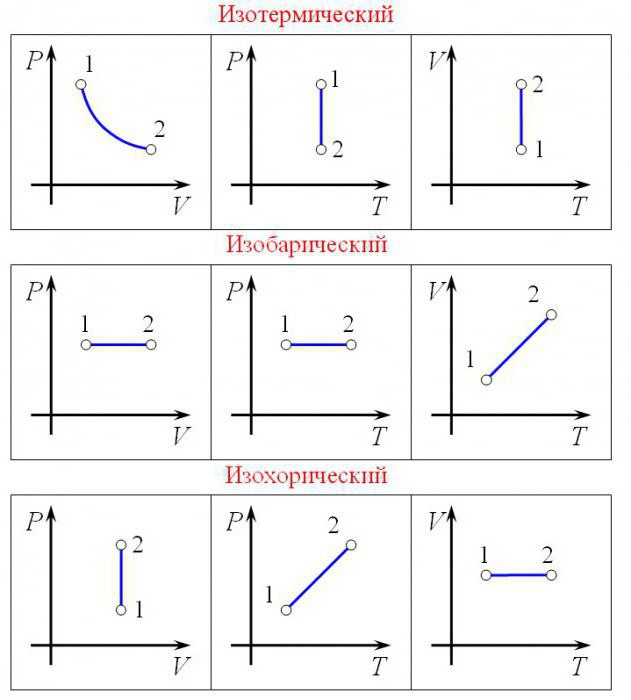
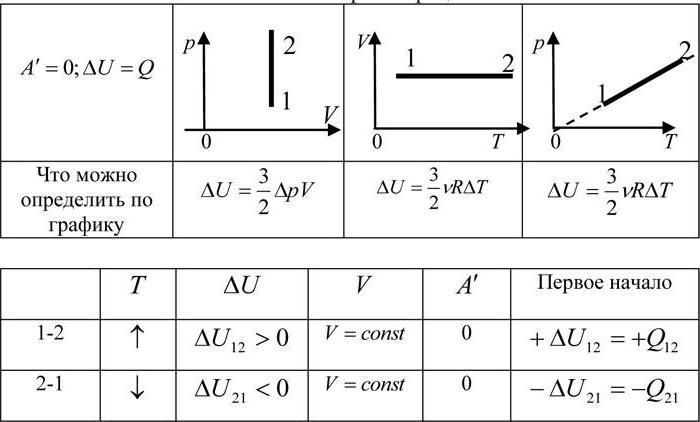
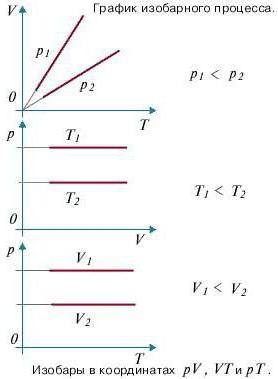
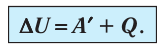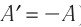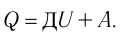Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Примеры

Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Обратимость

Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.

Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.

Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Вывод закона Гей-Люссака (первичное понимание)

Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.

Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Получение универсальной газовой постоянной

Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?

Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.

По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).

Видео:Адиабатный процесс. 10 класс.Скачать

Уравнение Менделеева-Клапейрона

Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.

Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.

Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.

В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.

Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Работа газа при изобарном процессе

Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ — это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.

Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.

Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.

Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.

Видео:Физика 10 класс Расчет количества теплоты для изобарного процессаСкачать

Универсальная газовая постоянная и ее смысл

Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Заключение

Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное — при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Изобарический процесс

Вы будете перенаправлены на Автор24

Видео:Физика Какая доля количества теплоты, переданного гелию при изобарном расширении, расходуется наСкачать

Что такое изобарический процесс

Изобарическим (или изобарным) процессом называется процесс, происходящий в неизменной массе газа при постоянном давлении.

Запишем уравнение для двух состояний идеального газа:

[pV_1=nu RT_1left(1right),] [pV_2=nu RT_2 left(2right).]

Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:

Уравнение (4) называют законом Гей-Люссака.

Видео:физика 10 класс. Расчет количества теплоты.Скачать

Внутренняя энергия и количество теплоты изобарического процесса

Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:

где $delta Q $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, $dA$- элементарная работа, которую совершает газ в процессе, i-число степеней свободы молекулы газа, R — универсальная газовая постоянная, d — количество молей газа.

Изменение внутренней энергии газа:

Уравнение (8) определяет работу для изобарного процесса. Вычтем из (2) уравнение (1), получим еще одно уравнение для работы газа в изобарном процессе:

[p_2-V_1)=nu R_2-T_1)to A=nu R_2-T_1) (9)] [triangle Q=fracнR_2-T_1)+nu R_2-T_1)=c_nu triangle T (10),]

где $c_$ — молярная теплоёмкость газа при изобарном процессе. Уравнение (10) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $triangle T.$

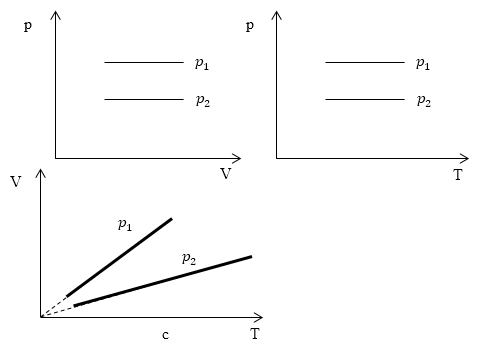
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой (рис.1).

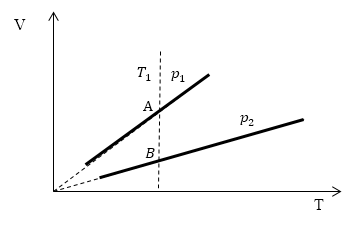
Задание: Определите, как соотносятся давления $p_1$ и $p_2$ на диаграмме V(T) рис 1с.

Проведем изотерму $T_1$

В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля — Мариотта:

[p_AV_A=p_BV_B (1.2)] [V_A > V_Bto p_A Ответ: Давления $p_1 > p_2$.

Готовые работы на аналогичную тему

Задание: При неизменном давлении p=3$cdot ^5$Па газ расширился от объема $V_1=2л$ до $V_2=4л.$ Найти работу, совершаемую газом.

За основу решения задачи примем формулу работы при расширении газа в изобарном процессе:

Переведем данные объемы в СИ: $V_1=2л=2^м^3$, $V_2=4л=4^м^3$

Ответ: Работа газа в изобарном процессе 600 Дж.

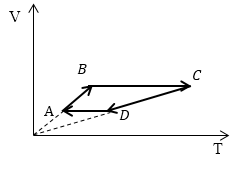
Задание: Сравните работу газа в процессе ABC и работу над газом в процессе CDA рис 3.

За основу решения примем формулу, определяющую работу газа:

Из геометрического смысла определенного интеграла известно, что работа — есть площадь фигуры, которая ограничена функцией подынтегрального выражения, осью абсцисс, и изохорами в точках $V_1 и V_2$ (оси p(V)). Переведем графики процессов в оси p(V).

Рассмотрим каждый отрезок графиков процессов изображенных на рисунке (3).

АВ: Изохорный процесс (p=const), $Vuparrow left( Объем растетright), Tuparrow $;

ВС: Изохорный процесс (V =const), $Tuparrow $ (из графика), p$uparrow $, из закона для изохорного процесса ($frac

=const$);

CD: (p=const), $Vdownarrow , Tdownarrow ;$

DA: (V =const), $Tdownarrow , pdownarrow .$

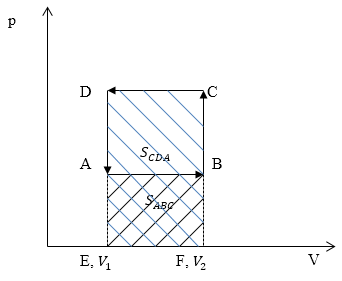
Изобразим графики процессов в осях p(V) (рис.4):

Работа газа $A_=S_$ ($S_$ — площадь прямоугольника ABFE) (рис. 3). Работа над газом $A_=S_$ ($S_$)$ -площадь прямоугольника $EFCD.Очевидно, что $A_>A_.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 18 12 2021

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Первый закон термодинамики — формулы и определение с примерами

Содержание:

Первый закон термодинамики:

При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода?

В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.

Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:

Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (

Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.

Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом.

Видео:Количество теплоты | Физика 10 класс #40 | ИнфоурокСкачать

Изохорный процесс

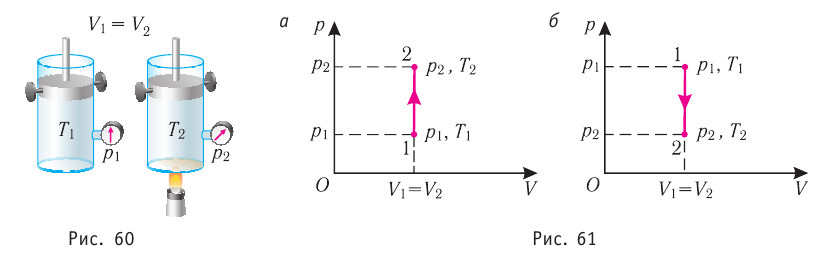
Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид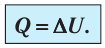
(11.З)

Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 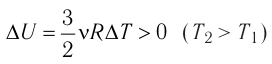(рис. 61, а). А если газ при изохорном

процессе отдаёт количество теплоты, то его внутренняя энергия убывает:

(рис. 61, б).

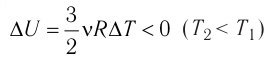
Видео:Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Изотермический процесс

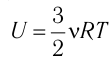
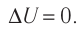
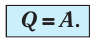
Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа остаётся постоянной, а её изменение Тогда первый закон термодинамики примет вид
(11.4)

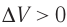
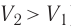
Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (, поскольку ) (рис. 62), то работа силы давления расширяющегося газа А > 0 (рис. 63, а). При одинаковой первоначальной температуре термостата и газа теплопередачи не происходит. Положительная работа силы давления расширяющегося газа совершается за счёт уменьшения его внутренней энергии, а значит, и температуры. Тут же возникает теплопередача от термостата газу. При медленном перемещении поршня в сосуде температура газа успевает выравняться, а реально происходящий процесс близок к изотермическому процессу, при котором расширяющийся газ получает некоторое количество теплоты (Q > 0) от термостата.

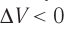
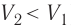
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (, так как ), то работа силы давления при сжатии газа А 0.

Видео:Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать

Изобарный процесс

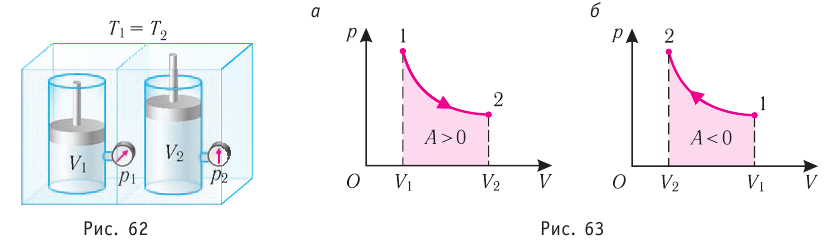
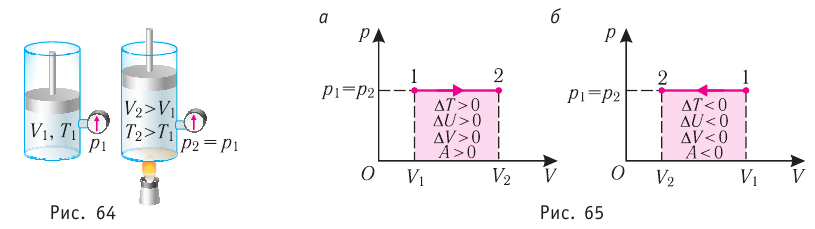
Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии 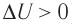) системы и частично идёт на совершение работы силой давления газа при его расширении (A>0)(рис. 65, a):

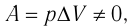
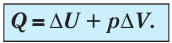
При изобарном процессе работа расширения (сжатия) газа , и первый закон термодинамики принимает вид

(11.5)

При изобарном сжатии газа внешние силы совершают работу А’ > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎬 Видео

Урок 109 (осн). Задачи на вычисление количества теплотыСкачать

Уравнение теплового баланса, термодинамика в изопроцессах | Физика ЕГЭ 10 класс | УмскулСкачать

Количество теплоты, удельная теплоемкость вещества. Практическая часть - решение задачи. 8 класс.Скачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Физика. МКТ: Изобарный процесс. Центр онлайн-обучения «Фоксфорд»Скачать