Уравнение теплопроводности в двумерном случае (7 видео)

Уравнение теплопроводности в двумерном случае

11.1.2. Пример: уравнение диффузии тепла

На протяжении всей главы мы будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.

Двумерное динамическое уравнение

Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:

Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа: Δ u ).

Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 11.1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция φ (x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.

Рис. 11.1. Физическая модель, описываемая двумерным уравнением теплопроводности

Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:

граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области;
начальное условие, т. е. функцию u (х, у, t) .

Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций.

Стационарное двумерное уравнение

Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 11.2 в виде поверхности u(х,у) .

Рис. 11.2. Решение стационарного двумерного уравнения теплопроводности (см. листинг 11.7 ниже)

Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения φ -φ /D ) следующим образом:

Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (11.2), принимающее вид Δu =0 , называют уравнением Лапласа.

Одномерное динамическое уравнение

Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 11.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:

Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 11.4.

Начиная с версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять встроенную функцию pdesolve .

Рис. 11.3. Физическая модель одномерного уравнения теплопроводности

Рис. 11.4. Решение одномерного уравнения теплопроводности (см. листинг 11.1 ниже)

Линейное и нелинейное уравнения

Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.

Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно).
Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t) , т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и.

Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.

Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.

Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u ) и ф(и) . В частности, для металлов в большинстве случаев можно считать, что D=const , в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.

Обратное уравнение теплопроводности

Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:

Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.

Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 11.1 или 11.2 заменить значение коэффициента диффузии на отрицательное число, например, D=-1 ), то мы получим заведомо нефизичное решение. Оно показано на рис. 11.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма (как для ситуации, рассмотренной в разд. «Устойчивость»этой главы), а определяется спецификой самой задачи.

Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.

Рис. 11.5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры (см. листинг 11.2 ниже с параметром D=-1)

Содержание

Двумерное уравнение теплопроводности. Фролова Ксения. 6 курс
Содержание
Постановка задачи [ править ]
Используемый метод [ править ]
Реализация [ править ]
Результаты [ править ]
Двухмерная стационарная теплопроводность
Двухмерная стационарная теплопроводность
🎬 Видео

Видео:Двумерное нестационарное уравнение теплопроводности в MatLab l 2D Heat transfer equation in MatLabСкачать

Двумерное уравнение теплопроводности. Фролова Ксения. 6 курс

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Содержание

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

Постановка задачи [ править ]

Необходимо решить задачу Коши для двумерного уравнения теплопроводности (дифференциальное уравнение в частных производных второго порядка, которое описывает распределение температуры в заданной области пространства и его изменение во времени.) с использованием средств параллельного программирования на основе MPI. Задача решается для однородного уравнения теплопроводности (система теплоизолирована) в области [0..L]x[0..L]:
[math]frac — a^2(frac+frac) = 0[/math]
[math]U(t=0) = U_0[/math]
при граничных условиях:
[math] U(x,y,t) = beginT_0, x=0\ T_1, x!=0 end[/math]
Используемые величины параметров:
[math]L=1, T_0=100, T_1=0[/math]

Видео:Уравнение теплопроводности на полупрямой (решение задачи)Скачать

Используемый метод [ править ]

В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI — это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).

Видео:Уравнение теплопроводности. Операционный методСкачать

Реализация [ править ]

При решении поставленной задачи будем использовать замену частных производных в дифференциальных уравнениях их разностными аналогами. Сеточный метод, основанный на замене в дифференциальном уравнении производных конечными разностями, называют методом конечных разностей, а сеточную схему такого метода — конечно-разностной.
По аналогии с одномерной задачей для уравнения теплопроводности вводим явную конечно-разностную схему. Область [0..L]x[0..L] разбивается на подобласти согласно количеству процессов в выполняемой параллельной программе. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага.
Программа для решения двумерного уравнения теплопроводности: программа

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Результаты [ править ]

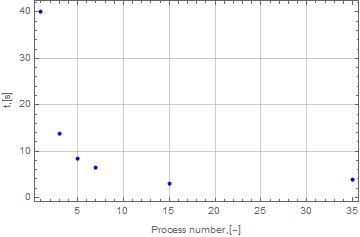
Найдено решение однородного уравнения теплопроводности в двумерной постановке для следующей сетки узлов: 300х300.

Количество процессов [-]	Время рассчета [сек]
1	40.2082
3	13.7626
5	8.38831
7	6.56195
15	3.08675
35	3.90614

Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано — выигрыш во времени либо незначителен, либо же затраченное время увеличивается.

Видео:Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать

Двухмерная стационарная теплопроводность

Видео:Решение неоднородного уравнения теплопроводностиСкачать

Двухмерная стационарная теплопроводность

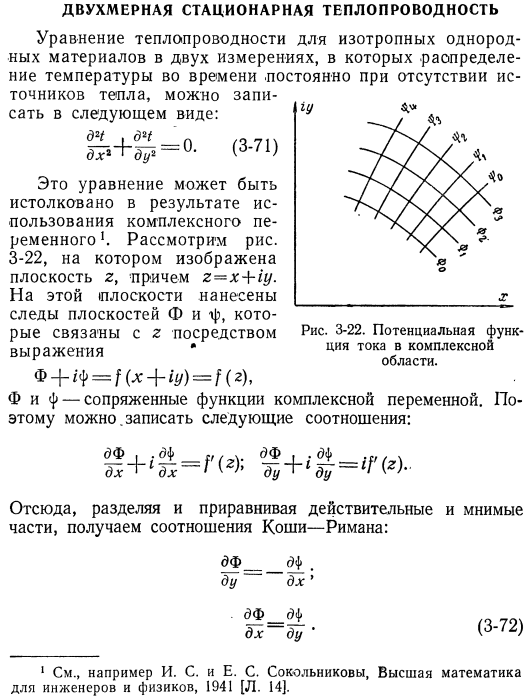
Уравнение теплопроводности для 2-мерного изотропного однородного материала. Распределение температуры во времени является постоянным заочно. Источник тепла можно описать следующим образом: (w-Х1） Это уравнение можно интерпретировать как результат использования комплексной переменной. 3-22, z = x + iy показывает плоскость z. Эта плоскость имеет трассировку плоскостей f и-f, которые связаны с z формулой f. φ +φφ= /（^ + ‘/）= /（2）.

Рисунок 3-22. Потенциальная текущая функция в сложном регионе. φ и φ-сопряженные функции комплексных переменных. Таким образом, можно записать следующие отношения: Df_ _ df. Do это. ДТ__д±ДХ-ду ’ (3-72） 1 например, И. С. И Е. С. Сокольниковы, высшая математика для инженеров и физиков, 1941 [Л. 14]. * Следовательно, трассировки Ф= const и ф= const ортогональны друг другу. То есть перпендикулярно друг другу на пересечении. Другая 1 характеристика сопряженной функции заключается в том, что каждая из них удовлетворяет уравнению Лапласа.

Таким образом, деление и уравнивание действительной и мнимой частей дает отношение между Коши и Риманом. Людмила Фирмаль

Это свойство может быть обозначено дифференцированием выражения (3-72) на части, сначала по отношению к x, затем к y, следующим образом: ^ 2Ф _ d2f _d ^ dh dh 2 dhdu du2 И затем d2f, d2f, d2f_, д2б. Du2 ’ДХ ду ДХ ду dh2′ Из этих соотношений мы получаем 2 уравнения Лапласа. 02ф (? Ф. Dh2, t, du2 ’ л. Dh2 ’du2′ (3-73） Если предполагается, что φ= /указывает температуру, то φ должно быть связано с q*, поскольку оно должно указывать на тепловой поток. Давайте рассмотрим фотографию. На рис. 3-23 показана система координат$, n. N перпендикулярно изотермам, а s касательно к изотермам в той же точке.

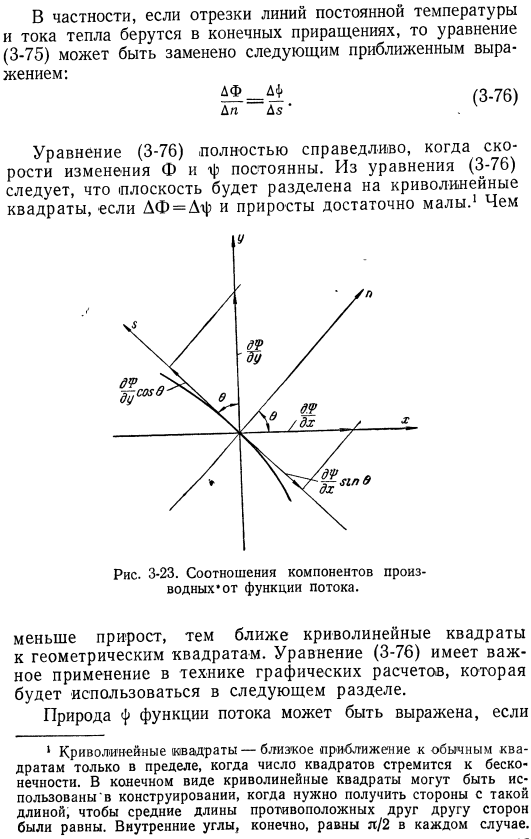
Тепловой поток, направленный вдоль n, можно описать следующим образом: в ДФ. Использование df — _d, cₒₛ0 _ _ x sin 0. ДФ * ДП» Если эти условия используются по отношению к выражению (3-72), то это выражение имеет вид: — 2С = — Лc⁰s⁰isⁱⁿ ^ =-• (3-74） [Уравнение (3-74) показано на рис. От 3 до 23. [] Поэтому ДП ДС ’ (3-75） * Сопряженная функция уравнения Лапласа обычно называется потенциальной функцией и функцией потока. Здесь это соответствует температуре и тепловому потоку соответственно. В частности, если отрезок прямой постоянной температуры и теплового потока получается с конечным шагом, то формулу (3-75) можно заменить следующей приближенной формулой: Жизнь: lf-lf. (3-76） ДП Д $. 7.

Формула (3-76) совершенно справедлива, когда скорость изменения φ и φ постоянна. Из Формулы (3-76) следует, что если рост достаточно мал при df = df, то плоскость разбивается на квадраты кривой. Рисунок 3-23. Доля производной * компонента функции потока. Чем меньше коэффициент усиления, тем ближе изогнутый квадрат к геометрическому квадрату. Формула (3-76) имеет важное применение для графического метода расчета, используемого в следующем разделе. Характер функции потока φ равен 1 1 изогнутый квадрат-приближение, близкое к обычному квадрату, только если число квадратов стремится к infinity. In окончательную форму, изогнутый квадрат можно использовать в строительстве, когда необходимо получить стороны такой длины, чтобы средняя длина противоположных сторон была равна друг другу.

Этот метод основан на свободной руке эскиза обтекаемой (streamline) и потенциальной линий, согласно правилам, относящимся к квадратуре квадрата кривой. Таким образом, сетка линий тока или фи потечет. Ниже приводится описание этого метода. Представьте себе коробку (рис. 3-25). Верхняя и нижняя поверхности имеют постоянную температуру t1 и 6 соответственно, остальные поверхности полностью изолированы. Верхняя поверхность может быть полностью удалена с образованием любого количества проходов в тепловом потоке (токовой трубке).

Линии, которые рисуют изотерму, могут быть нарисованы интервалом a / / » ar / = ax и ортогональными условиями изотермы и линии (теплового потока на их пересечении. Тепловой поток через трубку теплового потока БК = — uax- ^. (От 3 до 80） Выражение (3-80) может быть записано так же, как выражение (3-78) для условия Дг/ =дх. — (3-81） Необходимо продолжать строительство до тех пор, пока поле потока не будет exhausted. As в результате, существует nc ток трубки, n temperature температура a / rise. Весь тепловой поток в организме, по-видимому, является суммой роста теплового потока за счет общей разности температур. _9_—^ ы- (т _____ /） l«nbyby (3-82） Здесь, / j > t₂. При построении использовался dx = at /;. Отсюда = (3-83） Отношение nc / nr = t-это коэффициент формы объекта.

Форм-фактор тела-это чисто геометрическая величина, которую можно определить только один раз для любой заданной вещи 1 термин «форм-фактор» часто используется при изучении теплопередачи и каждый раз имеет разное значение, так что читатель может легко понять это. Общим для всех форм-факторов является определение geometry. So, в каждом отдельном случае он определяется только один раз для каждого рассматриваемого органа. Система.

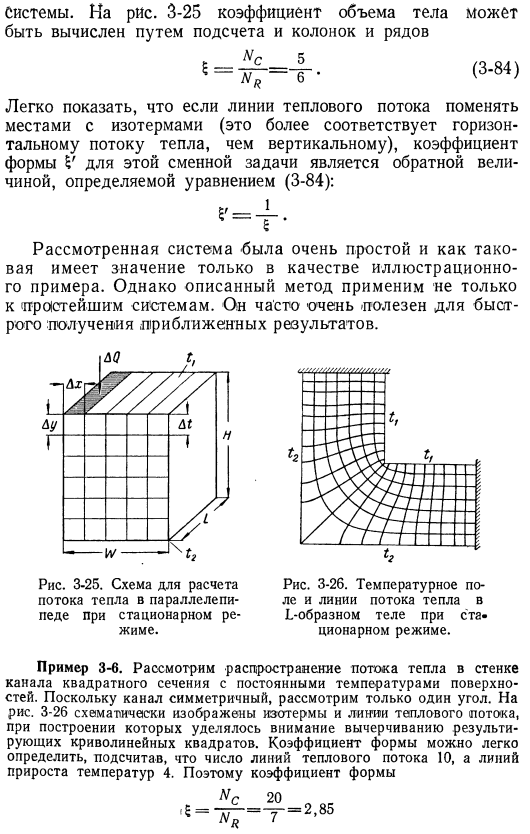
Рис. 3-25 соотношение объема тела может быть рассчитано путем подсчета как столбцов, так и строк nᵣ5 Легко показать, что коэффициент формы v для этой взаимозаменяемой задачи является обратным, определяемым формулой (от 3 до 84), когда тепловой поток обменивается с изотермической линией (это соответствует горизонтальному тепловому потоку, чем вертикальному направлению). ： Рассмотренная система достаточно проста, поэтому заслуживает лишь в качестве наглядного примера. Однако описанный метод (он применяется не только к самым простым системам, его можно применять только в самых сложных случаях). Часто бывает очень полезно быстро получить приблизительный результат. Рисунок 3-25.

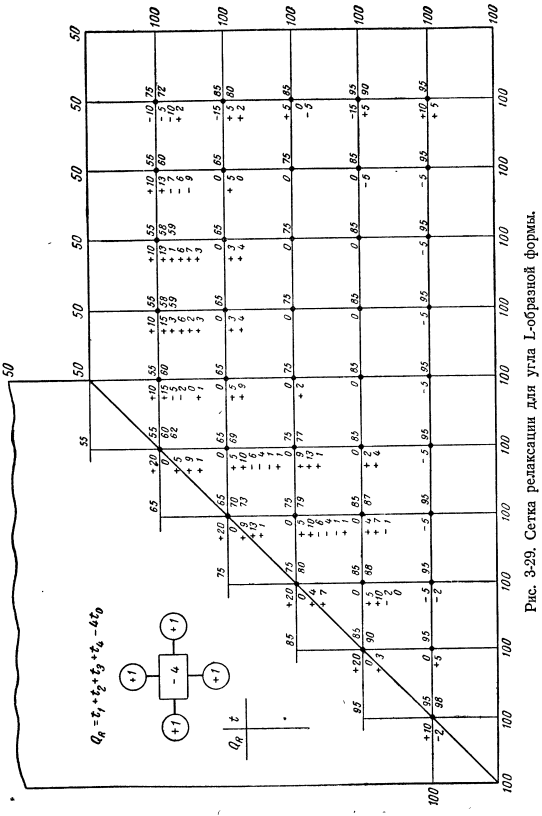
Предложена схема расчета теплового потока параллелепипеда в стационарном режиме. Рисунок 3-26. Температурное поле и тепловые линии течения Г-образного тела в стационарном состоянии. Пример 3-6 рассмотрим распространение теплового потока на стенке квадратного канала с постоянной температурой поверхности. Поскольку канал симметричен, рассмотрим только 1 угол. На рис. 3-26 представлено схематическое представление Изотерм и линий теплового потока, на структуру которых обращено внимание при нанесении полученного криволинейного квадрата. Форм-фактор может быть легко определен путем вычисления 10 линий теплового потока и 4 линий повышения температуры. Следовательно, фактор формы КС 20. 2. 85 ’5 = 7.

И тепловой поток, передаваемый за счет теплопроводности, q = 2. 85 x£ (/, -/.). Тепловой поток можно рассчитать, зная свойства материала, из которого изготовлены стенки канала и перепад температур по толщине стенок1. Рисунок 3-27. Система координат релаксационного метода. Релаксационный метод. Решение двумерного уравнения теплопроводности с источником тепла или без него представляет собой численный метод, разработанный Саутвеллом[l. 16, 17, 18], называемый релаксационным методом. Этот метод (в основном используется для решения уравнения Лапласа-Пуассона, но обсуждение здесь связано с проблемой теплопроводности.

В стационарных режимах без внутреннего источника тепла уравнение Лапласа является дифференциальным уравнением, решение которого определяется в результате с учетом соответствующих граничных условий. Поле в корпусе без источника тепла: — y + > = ° — (w — ⁸⁵ ） Рассмотрим точку* * п (х, г) тела, через которые проходит декартовой системы координат (рис. 3-27). Другими точками этого тела являются: p (x — — yy), p (x, y — — a), p (x-a, y), p (xy y-a). Для удобства они пронумерованы 1, 2, 3 и 4 соответственно. Если вы знаете температуру точки p (x, y), вы можете использовать ряд Тейлора для вычисления температуры окружающих точек с произвольной точностью. Например, если взять точку p (x, y) как ноль, то она выглядит так: З«+ (^-) ₀a + 4+©•• (3-86） 1 существует множество методов, основанных на сходстве теплопроводности и электропроводности, расхода жидкости и др.

Это может быть использовано для получения графического изображения желаемой формы или для приблизительного определения коэффициента формы. Наиболее распространенной из этих систем является p. j. schneider, «теплопроводность», ch. 13. 45] *. *Есть русский перевод. Пожалуйста, обратите внимание Третий Если вы объедините уравнение (3-86) с (3-87), вы получите: ^ + Г = 2 /₀+ (^ а! + О (а ’), (3-88） Где o (a⁴) обозначает остаточный член порядка a⁴. Выражение (3-88) может быть явно записано в (d2t/dx2) ₀. Члены Для создания новой папки можно использовать следующую команду Подобный. Людмила Фирмаль

Целью данного метода является установление такого температурного поля на теле, причем его температурное поле удовлетворяет формуле (3-90). Для этого систематически определяют избыточное qₒ. Qо-ТИ + ^ 2 +t₃+ (3-91） И задача обнуления остатка для каждой точки тела сводится к минимуму. Но когда температура самой точки изменяется на 1, оставшееся qo изменяется±4. It есть Ключ к вычислениям. На рис. 3-28 показана удобная модель смягчения последствий. Следующий простой пример полностью описывает этот»процесс». * Пример 3-7. As примером того, как это сделать, рассмотрим l-образный угол. Такой угол показан на рисунке. 3-29.

Температура границ стен является постоянной. Начальное распределение температуры Принимаются соответствующие граничные условия. Величина распределения температуры показывает кадр из узла. Следующим шагом является вычисление остатков для каждого узла с использованием соответствующей модели релаксации*. Это модель уравнения Лапласа в данном случае, потому что нет источника тепла. Остатки появляются слева от узловой точки. Воздействуя на самый большой остаток, он перемещается от точки к точке, изменяя температуру, чтобы уменьшить остаток. Рисунок 3-28. Схема расчета методом релаксации уравнения Лапласа. В этом случае не стоит стремиться точно установить temperature. As при экспериментальной работе навык приходит с практикой.

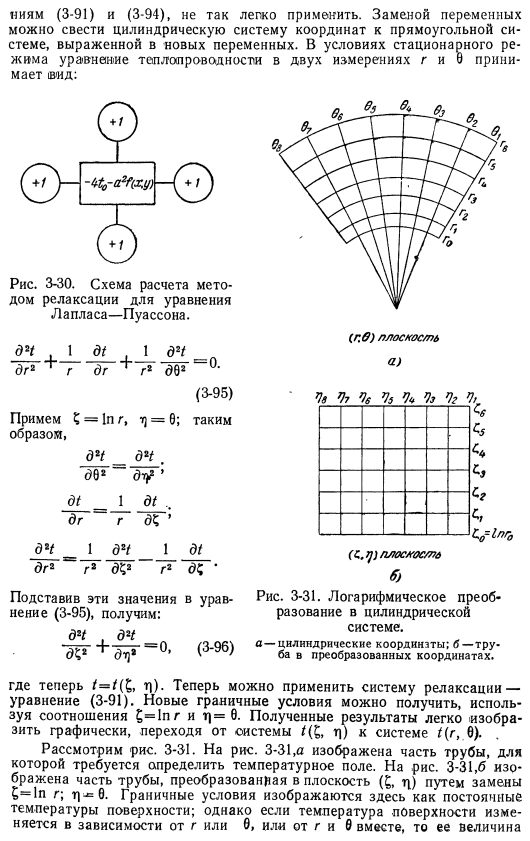
На рисунке показаны некоторые начальные расчеты, иллюстрирующие этот подход. Из-за симметрии, расчеты были сделаны только около половины угла. Если рассматриваемый объект имеет источник тепла, то уравнение теплопроводности принимает вид уравнения Пуассона. ——— x. ———- С. ）- (3-92） Если мы снова используем частичное выражение, оно выглядит так： А + г + ^ 4-4/₀. — ДГ — — — — — — — + О (А *) = Ф (Х, г). (3-93） Остаток qₒ в этом случае игнорирует 4-е или более высокие члены и принимает следующий вид: ^ o =Л4- / ₂4 — ^ 4 — ^-4 /о-а2/ (x, y). (3-94） Для выражения (3-94) необходимо изменить модель смягчения, как показано на рисунке 5. 3-30 отображает термин a2f (x, y), который характеризует рассеивание тепла. Очевидно, что источник тепла может быть произвольно распределен по всему телу, и это распределение представлено точками при расчете. Таким образом, источник тепла является своеобразной коррекцией эффекта изменения в нулевых точках. Метод релаксации также может быть использован в цилиндрической системе координат.

Однако в этом случае уравнение соответствует уравнению Рисунок 3-29. L-образная угловая релаксационная сетка. 0/705 9, 73. А и −6 * /〜И −1. 1 Около 75 0 Ниям (3-91) и (3-94) не так легко apply. By подставляя переменные, можно свести цилиндрическую систему координат к прямоугольной системе, представленной новыми variables. In стационарное состояние, 2-мерные g и 9 тепловых уравнений принимают вид: Рисунок 3-30. Релаксационная схема уравнения Лапласа-Пуассона. Д’t1 д /■1d2t рп2⁺г д-р⁺g2602°* (3-95） Вы принимаете это? = g, t] = 6; Вот так Д2/ _d2t. 692dt? * ДТ __ ДТ 1 ДГ г ДК ’ d’t _ 1d2t1 dt dr2s7r » d52’r2dc * (d. 0) самолет (c, tj) плоский / l б. ） Рисунок 3-31. Логарифмическое преобразование в цилиндрической системе. А-цилиндрические координаты; б-трубы преобразованных координат. Если подставить эти значения в Формулу (3-95), то получим: Д2/. Д2Т. Дв ^chj2 «»⁰ ⁰f3″⁹⁶） Здесь/ / / (ξ, η) -можно применить релаксационную систему-уравнение (3-91).

Новые граничные условия могут быть получены с использованием ξ=1πη и η=. Полученные результаты можно легко выразить графически, передав их из системы / ξ (η) в систему/ (r, 0). 。 Давайте рассмотрим фотографию. 3-31. На рис. 3-31 показана часть трубы, необходимая для определения температурного поля. На рис. 3-31. 6 показан участок трубы, преобразованный в плоскость (£, l) путем замены£= 1n g. L — ^ b-граничное условие изображено здесь в виде постоянной температуры поверхности. Однако, если температура поверхности изменяется в соответствии с r или 0, или r и 9, ее значение На границе точка (£, 7]) соответствует той же точке преобразования на плоскости. Вы можете рассчитать температуру каждой точки, применив прямоугольную релаксационную сетку непосредственно к шаблону плоскости (£, m|).

Поскольку это уже установлено, значения температуры этих точек связаны с точками на плоскости с помощью членов преобразования (r, 6). Поэтому проблема решена. Задачи 3-1. Напишите уравнение для зависимости длины температурного поля конического ребра. Основание конического ребра имеет радиус b и угол a на вершине. Температура основания считается постоянной. 3-2. Измерения, выполненные с помощью серии термопар, установленных на полубесконечном теле в направлении теплового потока, проводятся с помощью ДТ! Dx s) и d2t / dx2 0. Какие выводы можно сделать из этих экспериментальных наблюдений? 3-3. Они предложили нагревать воду с помощью калорифера диаметром 2, 5 мм и длиной 71 см на 2 киловатта. * Степень h, температура воды и выход 60°c Могу ли я использовать медную оболочку? 3-4. Трубы диаметром 20, 32 см прокладываются на глубине 76, 2 см от поверхности Земли.

Температура земной поверхности составляет 4, 4°c, температура стенок трубы-83, 5°c. С помощью графического дисплея потока можно определить устойчивый тепловой поток от трубы к земной поверхности. Сравните результаты этого измерения с результатами, полученными в результате расчетов. 3-5. Количество стекловаты и минеральной ваты требуется для утепления так, чтобы температура печи на кухне не превышала 58°с. Максимальная температура печи поддерживается термостатическим регулированием и достигает 288°с 3-6. Стенки холодильника утеплены стекловатой толщиной 7, 62 см, которая расположена между наружной и внутренней стенками холодильника. Поверхность внутренней стенки вблизи испарителя составляет 6, 6°С. Показания термометров, установленных на наружных стенках、 40, 7 ккал / м2-ч -, температура окружающей среды 32, 2°c Эффективна ли теплоизоляция? Если нет, то это указывает на причину низкой эффективности. 3-7.

Балка с прямоугольным поперечным сечением 100×6. 35 Х25. 4 мм, что очень долго по сравнению с другими измерениями, в которых течет ток, определяет температурное поле для установившегося режима. Балка изготовлена из меди и имеет температуру окружающего воздуха 18, 3°С. 3-8. Рассчитайте теплопередачу через стенки кругового цилиндра с эксцентрическими каналами. Наружный диаметр 20, 32 см, внутренний диаметр 12. 7 см, эксцентриситет 2, 54 см. Внутренняя температура поверхности составляет 121 ° с, наружной поверхности составляет 30°С.

Материал цилиндра является токопроводящей, не изолируя. 3-9. Завершите решение задачи, показанной на рисунке. 3-29. 3-10. Определить стационарную температуру нуля в любой точке p (t, 0) длинного стержня радиуса r. Половина поверхности хранит температуру tₐ при 0 6 l, а другая половина хранит температуру 0 2π.