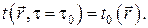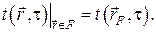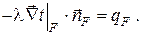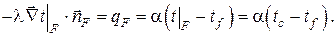При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.
Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:
Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.
Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.
Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q1 = -kSUx(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть Ux CpS∆x∆U = kSUx(x + ∆х, t) ∆t — kSUx(x, t)∆t.
Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:
Видео:Решение уравнения теплопроводности / граничные условия второго и третьего родаСкачать

Отсюда уравнение теплопроводности имеет вид
Ut = a 2 Uxx,
где 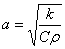
В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности
Начальные условия и граничные условия.
Для уравнения теплопроводности задается только одно начальное условие U|t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.
Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g1(t) ≡ Т1 и g2(t) ≡ Т2, где Т1 и Т2 — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т1= Т2 = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g1(t) = g2(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:
Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h1 > 0 — коэффициент теплообмена с окружающей средой, g1(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:
Аналогично получается условие (14) на правом конце стержня, только постоянная λ2 может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.
Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h1, очень большой.
Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:
Видео:Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.
Решение первой начально-краевой задачи для уравнения теплопроводности.
Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:
Найти решение уравнения
удолетворяющее граничным условиям
и начальному условию
Решим эту задачу методом Фурье.
Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).
Найдем частные производные:
Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Подставим эти производные в уравнение и разделим переменные:
По основной лемме получим
Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:
Шаг 2. Решим задачу Штурма-Лиувилля
Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.
Собственные значения равны
Собственные функции равны (См. решение задачи)
Шаг 3. Подставим собственные значения в уравнение а) и решим его:
Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Шаг 4. Выпишем частные решения уравнения (15):
В силу линейности и однородности уравнения (15) их линейная комбинация
Шаг 5. Определим коэффициенты An в (19), используя начальное условие (17):
Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам
Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).
Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения Ut = a 2 Uxx. Оно будет иметь вид
где
Краевые условия для уравнения теплопроводности
Дифференциальное уравнение теплопроводности в однородных изотропных средах в терминах математической физики есть неоднородное дифференциальное уравнение в частных производных параболического типа (первого порядка по времени и второго порядка по пространственным координатам). Если внутренние тепловыделения 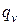
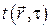
Как бы то ни было, любое дифференциальное уравнение может дать однозначное решение только если заданы условия однозначности. В случае дифференциального уравнения параболического типа должно быть задано начальное условие
Что касается граничных условий, то-есть условий теплообмена на границе рассматриваемого объёма с окружающей (контактирующей с ним) средой, то здесь имеют место несколько (а именно, четыре) возможностей, каждая из которых характеризует тот или иной тип теплового взаимодействия с внешней средой. Эти возможности обычно нумеруются римскими цифрами. Перечислим их.
Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

I. Граничные условия I рода
В этом случае задаётся распределение температур на физической границе рассматриваемого объёма, т.е. задаётся функция координат поверхности и времени
II. Граничные условия II рода
Задаётся плотность теплового потока на границе рассматриваемого тела, что позволяет записать
Такие граничные условия обычно имеют место при решении задач теплопроводности в твёрдых телах с теплообменом излучением на границах. Чаще всего такие задачи возникают при решении задач в металлургической теплотехнике, в астрофизике и т.д.
III. Граничные условия III рода
Граничные условия III рода наиболее распространены при решении задач теплопроводности в энергетике, в металлургии и в химической технологии.
Граничные условия III рода описывают в математической форме условия теплообмена внешней поверхности твёрдого тела с контактирующей с ним жидкостью или газом, т.е. со средами, допускающими конвективные движения с перемешиванием.
Видео:12. Как остывает шар (решение уравнения теплопроводности)Скачать

Математическая формулировка граничных условий III рода базируется на гипотезе (законе) Ньютона-Рихмана, согласно которой тепловой поток с поверхности к омывающей её жидкости пропорционален разности температур, т.е.
Здесь 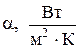
Экспериментальное обоснование гипотезы Ньютона-Рихмана состоит в том, что, как показывают экспериментальные исследования, количество теплоты, снимаемое с поверхности твёрдого тела, прямо пропорционально поверхности и разности температур поверхности и жидкости вдали от неё (как говорят, в ядре потока). Нахождение величины коэффициента теплоотдачи 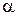
IV. Граничные условия IV рода
Граничные условия IV рода задают условия теплообмена на границе контакта твёрдых поверхностей. В частности, если контакт твёрдых поверхностей неидеален, то на границе их контакта в математическом смысле будет иметь место скачок температуры 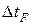
🎬 Видео
Термодинамика Л27. Уравнение теплопроводности. Граничные условия. Передача тепла через стенкуСкачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать

Закон и уравнение теплопроводностиСкачать

Вывод уравнения теплопроводностиСкачать

15. Решение уравнения теплопроводности в кругеСкачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Решение неоднородного уравнения теплопроводностиСкачать

12.1 Как остывает кирпич (уравнение теплопроводности)Скачать

Стационарное решение одномерного уравнения теплопроводности.Скачать

8.2 Теплопроводность на отрезке. Сложные задачи.Скачать

Решение задач теплопроводности (короткая версия)Скачать

Одномерное уравнение теплопроводности. Виды краевых задачСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 2)Скачать