Уравнение теплопроводности решение в маткад

11.1.2. Пример: уравнение диффузии тепла

На протяжении всей главы мы будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.

Двумерное динамическое уравнение

Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:

Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа: Δ u ).

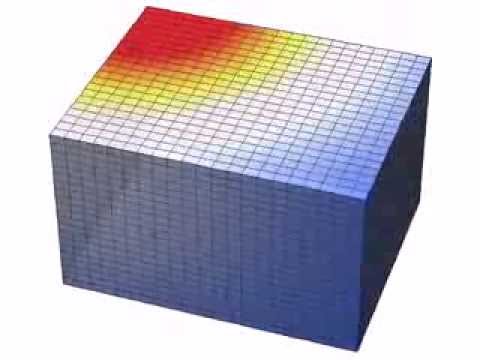
Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 11.1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция φ (x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.

Рис. 11.1. Физическая модель, описываемая двумерным уравнением теплопроводности

Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:

• граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области;
• начальное условие, т. е. функцию u (х, у, t) .

Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций.

Стационарное двумерное уравнение

Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 11.2 в виде поверхности u(х,у) .

Рис. 11.2. Решение стационарного двумерного уравнения теплопроводности (см. листинг 11.7 ниже)

Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения φ -φ /D ) следующим образом:

Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (11.2), принимающее вид Δu =0 , называют уравнением Лапласа.

Одномерное динамическое уравнение

Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 11.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:

Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 11.4.

Начиная с версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять встроенную функцию pdesolve .

Рис. 11.3. Физическая модель одномерного уравнения теплопроводности

Рис. 11.4. Решение одномерного уравнения теплопроводности (см. листинг 11.1 ниже)

Линейное и нелинейное уравнения

Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.

• Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно).
• Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t) , т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и.

Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.

Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.

Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u ) и ф(и) . В частности, для металлов в большинстве случаев можно считать, что D=const , в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.

Обратное уравнение теплопроводности

Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:

Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.

Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 11.1 или 11.2 заменить значение коэффициента диффузии на отрицательное число, например, D=-1 ), то мы получим заведомо нефизичное решение. Оно показано на рис. 11.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма (как для ситуации, рассмотренной в разд. «Устойчивость»этой главы), а определяется спецификой самой задачи.

Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.

Рис. 11.5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры (см. листинг 11.2 ниже с параметром D=-1)

Видео:Нестационарное уравнение теплопроводности в матлабеl Time dependent heat transfer equation in MatLabСкачать

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПАКЕТЕ МАТЕМАТИЧЕСКИХ РАСЧЕТОВ MATHCAD

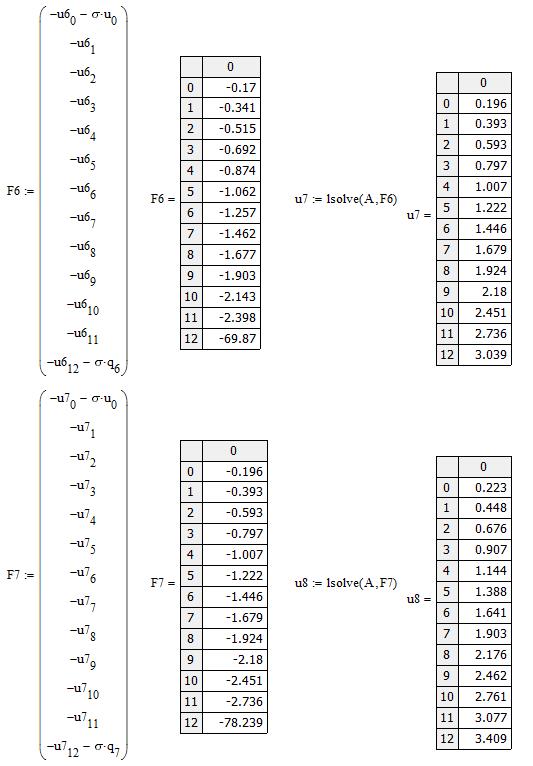
Введением конечно-разностных соотношений в уравнение теплопроводности – дифференциальное уравнение второго порядка в частных производных – отыскание решения уравнения свелось к определению решений систем линейных алгебраических уравнений относительно значений температуры в точках сетки. Эти системы могут решаться любым из методов решения систем линейных алгебраических уравнений. В пакете MathCAD существует функция решения систем линейных алгебраических уравнений методом Гаусса lsolve. Воспользуемся ею для получения решения уравнения теплопроводности (1.1) с начальным (1.11) и граничными (1.12) условиями. Аргументами функции lsolve являются матрица коэффициентов перед неизвестными и столбец свободных членов системы. В данном случае предстоит многократное решение системы с одинаковой матрицей коэффициентов. Изменяются столбцы свободных членов.

Начиная решение, введем исходные данные и вычислим значения температуры на нулевом временном слое по начальным условиям (1.11). Далее зададим матрицу коэффициентов системы — матрицу А и столбец свободных членов (1.18) (рис.3.1). Находим решение системы, т.е. температуру на первом временном слое u1, и показываем результат вычислений (рис.3.2). Определена температура для внутренних узлов сетки. Для того чтобы найти температуру на втором временном слое, нужно решить систему с измененным столбцом свободных членов. Для получения решения на втором временном слое нужно пересчитать свободный столбец системы и снова ее решить. Особенностью вычисления в пакете MathCAD является то, что индексы у векторов отсчитываются от нуля, поэтому появляется несоответствие в записи формул. Решение для второго слоя u2 приведено на рис. 3.3.

Рис. 3.1. Подготовка данных для решения уравнения теплопроводности на первом временном слое

Рис. 3.2. Решение уравнения теплопроводности на первом временном слое

Рис. 3.3. Решение уравнения теплопроводности на втором временном слое

Рис. 3.4. Полное решение в MathCAD

Повторяя вычисления столбца свободных членов и решения системы еще десять раз, получим вектора u1, u2, u3,…, u15, содержащие значения температуры во внутренних точках сетки. Полное решение представлено на рис. 3.4. Графическое полного решения можно увидеть на рис. 3.7.

Далее предстоит собрать в одну матрицу начальные значения, краевые и вычисленные во внутренних узлах.

Рис. 3.5. Формирование матрицы с результатами

Рис. 3.6. Результат решения уравнения теплопроводности

Видео:Двумерное нестационарное уравнение теплопроводности в MatLab l 2D Heat transfer equation in MatLabСкачать

Уравнение теплопроводности решение в маткад

Методические указания и контрольные задания к выполнению

лабораторной работы по курсу «Аналитические и численные методы решения уравнений математической физики» для студентов, обучающихся в магистратуре Хабаровск Издательство ТОГУ 2011 УДК 539.3/6. (076.5) Решение двумерной задачи теплопроводности методом конечных элементов в MATHCAD : методические указания и контрольные задания к выполнению лабораторной работы по курсу «Аналитические и численные методы решения уравнений математической физики» для студентов, обучающихся в магистратуре / сост. Л. М. Иванников. – Хабаровск : Изд-во Тихоокеан. гос. ун-та, 2011.

Методические указания составлены на кафедре «Механика деформируемого твердого тела». Включают содержание лабораторной работы и рекомендации к изучению разделов курса «Аналитические и численные методы решения уравнений математической физики», необходимых к ее выполнению, список рекомендуемой литературы и задачи для лабораторной работы.

Печатается в соответствии с решениями кафедры «Механика деформируемого твердого тела» и методического совета института строительства и архитектуры.

© Тихоокеанский государственный университет,

Видео:Mathcad-09. Пример: уравненияСкачать

ОБЩИЕ ПОЛОЖЕНИЯ

Целью лабораторной работы является усвоение алгоритма расчета двумерных задач теплопроводности методом конечных элементов.

Видео:Пример решения уравнения в MathCAD 14 (33/34)Скачать

УРАВНЕНИЕ ПЕРЕНОСА ТЕПЛА

Уравнение плоской задачи теплопроводности имеет вид [1] 2T ( x, y ) 2T ( x, y ) Ky Q( x, y ) 0, (1) Kx x 2 y кВт где K x, K y – коэффициенты теплопроводности в направлении осей x, y, ;

(м К ) T ( x, y) – искомая функция температуры; Q( x, y) – источник тепла внутри тела, кВт. Q( x, y) 0, если тепло подводится к телу.

м Граничные условия ставятся двух типов [2]:

T TГ (Г ), 1. (2) если температура T известна на некоторой части границы Г, где TГ (Г ) – известная температура в точках границы, зависящая от координат точек поверхности s на границе Г;

T ( x, y) T ( x, y) l Ky m h(T T) q( x, y) 0, 2. (3) Kx x y если на части поверхности Г 1 происходит конвективный теплообмен, характеризуемый величиной h(T T), или задан поток тепла q( x, y) на части поверхности Г 2, причем Г Г1 Г 2. Обозначения в (2) и (3): h – коэффициент кВт теплообмена, ; T ( x, y) – неизвестная температура на границе, К; T – (м2 К ) известная температура окружающей среды, К; l, m – направляющие косинукВт сы; q( x, y) – известный поток тепла,, считается положительным, если м тепло теряется телом. Поток тепла и конвективная теплоотдача на одном и том же участке не могут действовать одновременно.

Если имеет место теплоизолированная граница, то поток тепла равен нулю и конвективный теплообмен отсутствует, тогда граничное условие запишется так:

dT 0, dn где n – внешняя нормаль к границе рассматриваемой области.

Видео:Регулярный режим. Численное решение дифференциальное уравнение теплопроводностиСкачать

ФУНКЦИОНАЛ РЕШЕНИЯ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

Решение уравнения (1) по области s с граничными условиями (2) и (3) на Г эквивалентно отысканию минимума функционала При решении задачи МКЭ область s разбивается на n подобластей (конечных элементов), которые обычно принимаются в форме треугольников (рис. 1). Далее все формулы приводятся для треугольных КЭ. Функционал записывается как сумма вкладов всех конечных элементов по области. Тогда (4) примет вид проводности.

Или Представим температуру, изменяющуюся в пределах КЭ, через узловые значения:

где [ N (e) ] – матрица функций формы КЭ, учитывающая распределение температуры в пределах КЭ.

Тогда где [ B (e) ] – матрица градиентов функций формы КЭ.

Для каждого КЭ теперь можно записать вклад каждого КЭ в выражение для функционала (4):

Минимум функционала (4) требует выполнения следующего условия:

Для отдельного КЭ получим где матрица теплопроводности КЭ [k (e) ] имеет вид а вектор внешнего воздействия будет Для всей рассматриваемой области получим или где Уравнение (6) является основным уравнением для решения задачи теплопроводности методом конечных элементов.

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

ДВУМЕРНЫЙ СИМПЛЕКСЭЛЕМЕНТ

Для решения плоской задачи теплопроводности используется треугольный КЭ с прямолинейными сторонами (см. рис. 1). Нумерация узлов проводится против часовой стрелки, начиная с некоторого узла, обозначаемого единицей.

Нумерация сторон КЭ приведена на рис. 1.

Узловые значения температуры обозначаются T1, T2, T3. Температура в точке КЭ с координатами x, y определяется по формуле Ниже приводятся функции формы, применяемые для этого КЭ.

Площадь КЭ вычисляется по известной формуле Коэффициенты, входящие в функции формы, зависят от координат узлов, они приведены ниже:

Видео:6-1. Уравнение теплопроводностиСкачать

ПРИМЕНЕНИЕ ЧЕТЫРЕХУГОЛЬНЫХ КЭ ДЛЯ ГЕНЕРАЦИИ СЕТКИ

Для предварительного нанесения сетки с крупной ячейкой (разбивкой области на зоны) используются четырехугольные квадратичные элементы (рис. 2).

На каждой стороне КЭ вводится по три узла.

На рис. 2 показаны местные относительные координатные оси, в которых узел 7 ( 1, 1 ). Нумерация узлов такого КЭ, начиная с узла 1, проводится против часовой стрелки. Узлы 2, 4, 6, 8 могут располагаться в произвольной точке соответствующей стороны, что позволяет в дальнейшем строить более густую сетку вблизи точечных воздействий. В дальнейшем каждая сторона такого КЭ разбивается на заданное число участков. Нумерация узлов проводится следующим образом: по вертикали от узла с координатами ( 1, 1 ) вниз по оси и слева направо по оси. Таким образом, крупные элементы делятся на более мелкие, которые в свою очередь меньшей по длине диагональю разбиваются на треугольные КЭ. Треугольные участки зоны также представляются в виде четырехугольных квадратичных элементов (рис. 3).

Рис. 3. Представление треугольной области в виде четырехугольного квадратичного элемента

Видео:Решение задачи теплопроводности (Явная разностная схема)Скачать

МАТРИЦА ТЕПЛОПРОВОДНОСТИ КЭ

Для треугольного КЭ матрица теплопроводности имеет вид где L1 2, L2 3, L31 – длины соответствующих сторон КЭ. Последние три члена учитывают конвективный теплообмен по каждой стороне КЭ. Так как КЭ входит составной частью в рассматриваемую область, то конвективный теплообмен обычно происходит по одной или двум сторонам КЭ.

Видео:Mathcad-10. Пример: дифференциальные уравненияСкачать

ВЕКТОР ВНЕШНИХ ВОЗДЕЙСТВИЙ НА КЭ

Внешними (известными) воздействиями являются:

1. Источник тепла внутри КЭ постоянной интенсивности Q (e ).

2. Приток тепла за счет теплового потока q (e ).

3. Конвективный теплообмен не более чем по двум сторонам КЭ с коэффициентом теплообмена h (e ).

4. Точечный источник тепла Q * ( X 0, Y0 ), находящийся внутри КЭ.

Вектор внешних воздействий на КЭ имеет вид

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

ГРАДИЕНТЫ ТЕМПЕРАТУР И СРЕДНЯЯ ТЕМПЕРАТУРА ПО КЭ

Градиенты температур и средняя температура по КЭ вычисляются по следующим формулам:

Видео:Вывод уравнения теплопроводностиСкачать

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

Видео:Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

НАНЕСЕНИЕ СЕТКИ УЗЛОВ НА РАССМАТРИВАЕМУЮ ОБЛАСТЬ

Область решения задачи помещается в систему глобальных координат X, Y. Рассматриваемая область должна быть покрыта сеткой узлов. Чем меньше будет ячейка сетки, тем точнее будет решение задачи. Нанесение сетки проводится согласно [2] в 2 этапа.

I этап. Рассматриваемая область разбивается на ряд прямоугольных и треугольных зон (четырехугольные квадратичные элементы). Зоны нумеруются в произвольном порядке. Для каждой такой зоны задаются 8 узловых точек (по три на каждой стороне, включая угловые точки). Для треугольной зоны одна из сторон соответствует двум сторонам прямоугольника (5 точек).

Таким образом, при разбивке на зоны используются четырехугольные квадратичные элементы.

Составляются следующие таблицы исходных данных:

а) Табл. 1 соединения зон, определяющая, какие стороны зон контактируют между собой.

Соединение зон в рассматриваемой области. Таблица 1.

В приведенной табл. 1 показано, что зона 1 контактирует только с зоной по первой стороне, зона 2 контактирует с зоной 1 по первой стороне и с зоной 3 по четвертой стороне. Зона 3 контактирует только с зоной 2 по второй стороне (рис. 4). Нумерация сторон зависит от ориентации местных осей в относительных координатах,, которые показаны на рисунке жирными цифрами. На рис. 4 показано направление нумерации узлов зон от начального узла Н.

Рис. 4. Формирование таблицы соединения зон б). Табл. 2 координат узлов, нанесенных на границы зон, в принятой глобальной системе координат.

Координаты узлов на границах зон Таблица 2.

в). Табл. 3, в которой указывается число полос по вертикали и горизонтали, на которые разбивается каждая зона для получения сетки с ячейками меньших размеров.

Формирование сетки с меньшими по размеру ячейками Таблица 3.

Зона 1 разбивается на пять полос по высоте и шесть полос по ширине.

г). Табл. 4, в которой для каждой зоны указываются ранее нанесенные узлы.

Номера узлов предварительной сетки для каждой зоны Таблица 4.

В табл. 4 указано, что восемь узлом второй зоны имеют такие номера при обходе рассматриваемой зоны против часовой стрелки.

II этап. Далее в Mathcad реализована программа “grid” [2], в которой задается число полос по высоте и ширине для каждой зоны, позволяющее разбить каждую зону на прямоугольники гораздо меньших размеров. Затем каждый из этих малых прямоугольников меньшей по длине диагональю делится на два треугольника и вся рассматриваемая область покрывается сеткой с треугольной ячейкой.

В результате работы этой программы выдаются следующие данные:

a). Число треугольных КЭ (Kol_Elem).

б) Следующие табл. 5, 6, 7.

Нумерация узлов сетки по сторонам зон Таблица Таблица выдается в форме матрицы размером (число полос зоны по высоте число полос зоны по ширине) для каждой зоны, что упрощает построение сетки.

Приведенная матрица показывает, что в зоне 3 на стороне 1 располагаются узлы 23, 24, 25, 26; на стороне 2 располагаются узлы 26, 22, 1; на стороне 3 – узлы 1, 16, 13, 10; на стороне 4 узлы 10, 19, 23. Обход зоны против часовой стрелки. Эта нумерация показана в приведенном ниже примере.

Расположение КЭ и принадлежность узлов КЭ треугольной сетке Таблица Также могут быть выведены таблицы, связывающие номер зоны, номер КЭ и координаты узлов КЭ.

На схему рассматриваемой области вручную наносится сетка с нумерацией КЭ и их узлов.

Видео:1 Одно уравнениеСкачать

ФОРМИРОВАНИЕ ВЕКТОРА ВНЕШНИХ ВОЗДЕЙСТВИЙ

На основании построенной сетки для рассматриваемой области отмечаются:

а) Номера сторон, по которым происходит конвективный обмен тепла.

б) Номера узлов, в которых температура задана.

в) Номера КЭ, в которых на их сторонах, узлах или внутри располагаются сосредоточенные тепловые источники.

Составляются следующие табл. 8, 9, 10.

Стороны области с конвективной теплоотдачей Таблица Предполагается, что конвективный теплообмен возможен только по двум сторонам КЭ из трех.

Таблица точечных источников тепла Таблица Таблица величин температуры в узлах КЭ.

Таблица градиентов температур Gradx, Grady по осям Х и Y соответственно.

Таблица средней температуры Тsred по каждому КЭ.

Распределение температур по рассматриваемой области с указанием величин изотерм.

Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

В теплопроводящей среде проходят 4 кабеля, как показано на рис. 5. Среда имеет коэффициенты теплопроводности K x K y 10. Коэффициент тепсм К лообмена на поверхности среды h 5. По боковым сторонам рассматрисм 2 К ваемая среда ограничена толстым слоем изоляции. Температура воздуха на поверхности среды T 30 0 C. Температура нижнего слоя среды T 20 0 C.

Мощность излучения тепла каждым кабелем составляет Q 200 Вт.

1. Определить распределение температуры в заданной области.

2. Определить градиенты температур и среднюю температуру по области.

3. Построить графики изменения полученных величин.

а) при выполнении лабораторной работы учесть симметрию области и симметрию температурного воздействия;

б) разбить рассчитываемую часть области на три или четыре зоны;

в) каждую зону разбивать от трех до пяти полос по высоте и ширине для упрощения нанесения сетки на область.

Видео:Численное решение уравнения теплопроводностиСкачать

РЕШЕНИЕ ЗАДАЧИ

Учитывая симметрию рассматриваемой области, в расчете будем учитывать только половину этой области (рис. 6).

Поместим рассматриваемую область в систему глобальных осей X и Y и разобьем ее на три зоны, на стороны которых нанесем узлы, полагая зоны четырехугольными квадратичными элементами рис. 7. Пронумеруем зоны и узлы, обходя область против часовой стрелки. Для определения номеров сторон зон для каждой зоны устанавливается система местных осей,.

Рис. 7. Предварительная разбивка области на зоны Для более точного решения задачи необходимо узлы на границе зон располагать ближе к точечным источникам тепла.

Составляются исходные данные для назначенных зон и узлов (табл. 1, 2, 3, 4). Программа расчета выдает табл. 5, 6, 7, представляющие полную информацию о треугольной сетке, нанесенной на область, используемую в дальнейшем расчете. По этим таблицам на листе строится сетка (рис. 8).

Рис. 8. Треугольная сетка, нанесенная на область По полученной сетке проводится учет внешнего температурного воздействия и составляются табл. 8, 9, 10. После чего в табличной форме выводятся результаты решения задачи и их графическое представление на рис. 9 и

Видео:Стационарное решение одномерного уравнения теплопроводности.Скачать

1. Р Е З У Л Ь Т А Т Ы РЕШЕНИЯ ПО СОЗДАНИЮ СЕТКИ КЭ

Видео:Трёхмерное уравнение теплопроводности с ф.п. l 3D Heat transfer equation with phase change in matlabСкачать

УЗЛЫ СЕТКИ ПО ГРАНИЦАМ ЗОН

Видео:8. MathCad. Решение систем линейных алгебраических уравненийСкачать

ТАБЛИЦА КЭ

КООРДИНАТЫ УЗЛОВ КЭ

ФОРМИРОВАНИЕ ВЕКТОРА

ВНЕШНИХ ВОЗДЕЙСТВИЙ

2. Р Е З У Л Ь Т А Т Ы РЕШЕНИЯ ЗАДАЧИ

Градиенты температур и средняя температура по КЭ пературы по области

ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ

В теплопроводящей среде, как показано на схеме, проходят кабели, излучающие тепло. Среда имеет коэффициенты теплопроводности K x и K y. Коэффициент теплообмена на поверхности среды h. На некоторых участках рассматриваемая среда ограничена толстым слоем изоляции. Температура воздуха на отдельных участках среды, где происходит конвективный теплообмен, Т. На некоторых участках среды задана температура Т.

Мощность излучения тепла каждым кабелем составляет Q.

Требуется, используя исходные данные для своего варианта и схему задания (табл. 11, рис. 11):

1. Определить распределение температуры в заданной области.

2. Определить градиенты температур и среднюю температуру по области.

3. Построить графики изменения полученных величин.

ИСХОДНЫЕ ДАННЫЕ

Исходные данные к лабораторной работе по вариантам Таблица Ноh, анта Рис. 11. Схемы вариантов задний для лабораторной работы

КОНТРОЛЬНЫЕ ВОПРОСЫ

Запишите уравнение теплопроводности для двумерной задачи.

Запишите граничные условия для двумерной задачи теплопроводности.

Запишите полный функционал решения задачи теплопроводности.

Выведите основное уравнение для решения двумерной задачи теплопроводности методом конечных элементов.

5. Какие конечные элементы используются для решения двумерной задачи теплопроводности ?

6. Как определяются функции формы для двумерного симплексэлемента?

7. С какой целью используются четырехугольные квадратичные элементы?

8. Как выбирается система местных координат и проводится нумерация сторон четырехугольного квадратичного элемента?

9. Запишите матрицу теплопроводности для треугольного КЭ.

10. Как формируется матрица теплопроводности для рассматриваемой области?

11. Как формируется вектор внешних тепловых воздействий для КЭ?

12. Как формируется вектор внешних воздействий для рассматриваемой области?

13. Как определяются градиенты температур и средняя температура по КЭ?

14. Как проводится нанесение сетки на рассматриваемую область?

15. Какие исходные данные необходимо подготовить для нанесения сетки?

16. Какие выходные данные используются для построения сетки и как она наносится на область?

17. Какие данные необходимо внести для формирования вектора внешних тепловых воздействий?

18. Как учесть знак величины точечного источника тепла? Притока тепла?

19. Какие выходные данные получаются в результате решения задачи теплопроводности?

1. Зенкевич О. Метод конечных элементов в технике / О. Зенкевич. – М. :

Мир, 1975. – 452 с.

2. Сегерлинд Л. Применение метода конечных элементов/ Л. Сегерлинд. – М.:

Мир, 1979. – 392 с.

ОГЛАВЛЕНИЕ

ОБЩИЕ ПОЛОЖЕНИЯ ………………………………………………. Уравнение переноса тепла……………….…………………………… … Функционал решения задачи теплопроводности……………………. Двумерный симплекс элемент…………………..………………..…. Применение четырехугольных КЭ для генерации сетки. ……….… Матрица теплопроводности КЭ…………………….………………. Вектор внешних воздействий на КЭ….…………………………… …. Градиенты температур и средняя температура по КЭ…………… …… Порядок решения задачи теплопроводности в Mathcad 14…..….… ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ…….… ….. РЕШЕНИЕ ЗАДАЧИ……………………………………………………. Распечатка решения задачи……………………………………… …. ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ…. Контрольные вопросы…………………………………………… ……. Библиографический список……………………………………… ……

РЕШЕНИЕ ДВУМЕРНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ В MATHCAD

Методические указания и контрольные задания к выполнению лабораторной работы по курсу «Аналитические и численные методы решения уравнений математической физики» для студентов, обучающихся в магистратуре.

Главный редактор А. А. Суевалова Редактор Т. Ф. Шейкина Оператор компьютерной верстки Л. М. Иванников Подписано в печать Бумага писчая. Гарнитура «Таймс». Печать цифровая.

Усл. печ. л. Тираж 50 экз. Заказ Издательство Тихоокеанского государственного университета.

680035, Хабаровск, ул. Тихоокеанская, 136.

Отдел оперативной полиграфии издательства Тихоокеанского государственного университета. 680035, Хабаровск, ул. Тихоокеанская, 136.

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ВЫПОЛНЕНИЕ ТЯГОВЫХ РАСЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПРОГРАММНОГО КОМПЛЕКСА ЭРА Учебно-методическое пособие по курсовому и дипломному проектированию по дисциплине Изыскания и проектирование железных дорог ИРКУТСК 2010 УДК 11.03 ББК 39.21 В 92 Составитель: В.В. Четвертнова, к.т.н., доцент кафедры изысканий, проектирования, постройки железных дорог и управления недвижимостью Рецензенты: М.С. »

© 2013 www.diss.seluk.ru — «Бесплатная электронная библиотека — Авторефераты, Диссертации, Монографии, Методички, учебные программы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.