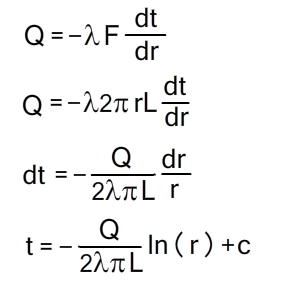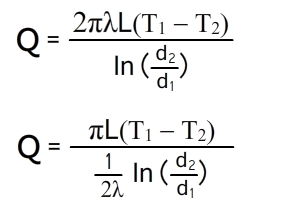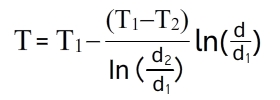Уравнение теплопроводности для двухслойной плоской стенки (8 видео)

Теплопроводность через стенку

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.

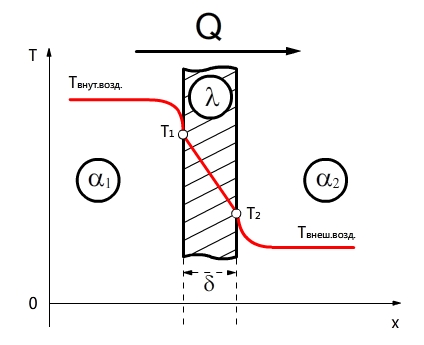
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.

Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).

Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.

Теплопередача через непроницаемую стенку включает в себя следующие процессы:

теплоотдачу от горячей среды к стенке;
теплопроводность внутри стенки;
теплоотдачу от стенки к холодной среде.

Содержание

Теплопередача через плоскую стенку (граничные условия первого рода)
Распределение температуры в плоской стенке
Теплопроводность через многослойную стенку
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Теплопроводность через многослойную плоскую стенку
Теплопроводность плоской, цилиндрической и сферической стенок при стационарном режиме
📸 Видео

Видео:Видео лекция.Теплопроводность через плоскую стенкуСкачать

Теплопередача через плоскую стенку (граничные условия первого рода)

Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.

Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.

Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).

Поверхностная плотность теплового потока рассчитывается по формуле:

где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].

На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:

где δ = dx — толщина стенки, λ

λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.

а обратная величина —

R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.

Для теплового потока формулу так же можно представить в виде:

Общее количество теплоты проходящее через площадь стены S за время t можно представить как:

Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Распределение температуры в плоской стенке

Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C₁; T=C₁х+С₂ (1). Определим С₁ и С₂ через граничные условия.

При х=0 T=T₁, подставим в уравнение (1) и получим T₁=С₂.
При х=δ T=T₂, подставим в уравнение (1) и получим T₂=С₁*δ+С₂, T₂=С₁*δ+T₁, получим: С₁=(Т₂-T₁)/δ. Теперь подставим в уравнение (1) найденные С₁ и С₂, получим следующее распределение температуры в нашей стене:

Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:

Видео:Теплопроводность плоской стенкиСкачать

Теплопроводность через многослойную стенку

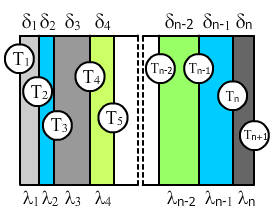
Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λ_i и разной толщиной δ_i.

Термическое сопротивление стенки считается так:

Для теплового потока формула будет иметь вид:

Температура на границе слоя вычисляется по следующей формуле:

Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:

Эквивалентная теплопроводность многослойной стенки:

Видео:Закон и уравнение теплопроводностиСкачать

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

q = k * (T_{возд.внутри} — T_{возд.снаружи}); Вт/м 2

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

Видео:Теплопередача через плоскую стенкуСкачать

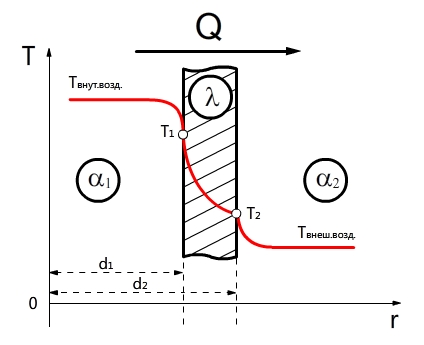
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Видео:6-1. Уравнение теплопроводностиСкачать

Теплопроводность через многослойную плоскую стенку

Теплопроводность многослойных плоских стен В тепловых устройствах стены часто состоят из нескольких плоских слоев из разных материалов. Руководство уравнение В этом случае предполагается, что все слои тесно выровнены друг с другом. Формула для расчета теплопроводности сложной стенки в стационарном состоянии может быть получена из уравнения теплопроводности.

Отдельные слои при условии, что тепловой поток через изотермическую поверхность неоднородной стенки одинаков. Чтобы решить эту проблему, рассмотрим трехслойную стенку с индивидуальной толщиной слоя 6 л, 62 т 63 и коэффициентами теплопроводности Xj, A и 3 соответственно (рис. 23-2). Межслойная

температура / с’л а Тепловой поток в каждом слое: — Q = t-0; Q =

-F (tcn — tcnY, 63 Решение этих уравнений для разности температур и сложение дает Рисунок 23-2 _ Q b; J, Q -TG t ‘sl-1sl Святой F 2 «Я сл F ^ г «у» В 63. Дж * В (6л j.?2 63 ‘cl-‘ cr-

—1 -: — и Откуда (23-8) F b F ч (И Я Т.е. для любого количества слоев Я = П Q = lF (t’r-rcr)) l £ f (23-9) / = 1 l * Соотношение называется термическим сопротивлением

слоя и Я = гг £ Ранг 2 ^ -Полное тепловое сопротивление многослойных плоскые и вводят эквивалентный коэффициент теплопроводности в уравнение (23-9) / я = т. (23-10) Сравнение уравнений (23-9) и (23-10) дает (23-11) / = п Я = н 2 £ Кк — 2 ^ j- I Эквивалентная теплопроводность многослойной стенки f равна теплопроводности однородной стенки такой же толщины, которая

их стен. ^ Иногда многослойные плоские стены рассчитываются как однородн Людмила Фирмаль

передает тот же тепловой поток при той же температуре поверхности. Значение Yaek зависит от термического сопротивления и толщины отдельных слоев. «Температура C между отдельными слоями сложной стены равна: (23-12) г- / ‘А- «W- ^ c -„. «H Hello tsl = ‘sl —- и т. д. / т лз Температура каждого слоя стенки с постоянной теплопроводностью изменяется линейно, а для многослойных плоских стенок график температуры представляет собой пунктирную

линию. Однослойная теплопроводность Цилиндрическая стена час t Наружная и внутренняя поверхности прямой цилиндрической трубки «поддерживаются при постоянной температуре / oT и / cT. Изотермическая поверхность представляет собой цилиндрическую поверхность с трубкой и осью. Поскольку температура изменяется

только в радиальном направлении, Расслоение также радиально, длина трубы бесконечна, в этом случае температурное поле одномерно. t = / (r), Где r — текущая цилиндрическая координата. Если температура неравномерно распределена по поверхности трубы, поле температуры не является одномерным, и последнее уравнение является недействительным. На фиг.23-3 показана труба с одним

тепловым потоком, направленным радиально. Получаем отрезок трубы длины. Поверхность F на расстоянии r от оси составляет 2lg /. Температура внутренней поверхности равна / st «external- / st-. После прохождения поверхности проходит тот же постоянный тепловой поток. Рисунок 23-3 Выберите кольцевой слой в стене с радиусом r и толщиной dr. Тогда он может принять поверхность, через которую

проходит тепловой поток. Это нужно рассматривать этот базовый слой как плоскую стену. Р Фурье (А) Q = -W (ди / др), Или для кольцевого слоя Q = — 2nrl (дт / др). Разделение переменных dt = — (Q / 2 нМ). (Dr / r). Интегрировать уравнение (а) в диапазоне r / r> от с / м до f dt = -J ( ул tcr-tct = (Q! 2nXl) In r2 / rlt Где% Q = / (/ st-Q / (1/2 $$ Ind2 / d>. (23-13) Как видно из уравнения, распределение температуры на

азница температур между поверхностями очень мала и равна dt. По методу Людмила Фирмаль

стенке цилиндрической трубы представляет собой логарифмическую кривую. Тепловой поток через цилиндрическую стенку определяется заданными граничными условиями и зависит от отношения внешнего диаметра к внутреннему диаметру. -Тепловой поток может быть обусловлен длиной единицы qt трубы и м2 внутренней или внешней поверхности q1 и q2. • Q 2l (/ rm- (st) / nd2 / di Q 2X (/ cr

/ Jr). ндил ди ин дзфди Q 2X. (/ St-fcr) dild2 d2 (23-14) (23-15) (23-16) I1 Мне 2

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Теплопроводность плоской, цилиндрической и сферической стенок при стационарном режиме

Уравнение теплопроводности для двухслойной плоской стенки

Рисунок 7.3 – К выводу уравнения теплопроводности плоской стенки

Теплопроводность плоской стенки. Тепловой поток перемещается через плоскую стенку толщиной δ (рис. 7.3) из однородного материала, имеющего коэффициент теплопроводности .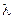

На наружной поверхности стенки поддерживаются постоянные температуры и ( > ). Температура изменяется только в направлении оси х, перпендикулярной плоскости стенки, т.е. температурное поле одномерно, а изотермические поверхности плоские и располагаются перпендикулярно оси х.

В соответствии с дифференциальным уравнением теплопроводности (7.23) .

В результате интегрирования этого выражения получим:

Таким образом, температура по толщине плоской стенки при установившемся тепловом режиме изменяется линейно, а градиент температуры сохраняет постоянное значение.

Константы интегрирования и определяют из граничных условий:

При , следовательно ;

При ,

С учетом найденных констант:

. (7.25)

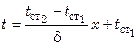
Дифференцируя последнее уравнение, имеем: .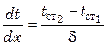

Подставив найденные значения температурного градиента в уравнение, выражающее основной закон теплопроводности (7.12), получим уравнение теплопроводности для плоской стенки при стационарном режиме:

, (7.26)

Рисунок 7.4 – К выводу уравнения теплопроводности плоской многослойной стенки

Отношение (l/d) носит название тепловой проводимости стенки, а (d/l) – термического сопротивления стенки.

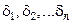
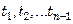
Если стенка многослойная(рис. 7.4), состоит из n слоев толщиной с коэффициентами теплопроводности соответственно, при этом температуры наружных поверхностей и , а температуры на границе слоев , то при установившемся тепловом режиме тепловой поток Q, проходящий через каждый слой, одинаков и уравнение теплопроводности для каждого из них может быть выражено уравнением (7.26):

для 1-го слоя , или ;

для 2-го слоя 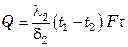, или ; (7.27)

для n-го слоя , или .

Складывая левые и правые части выражение (7.27), получим уравнение теплопроводности плоской многослойной стенки для стационарного режима:

, (7.28)

где i – порядковый номер слоя.

Таким образом, общее термическое сопротивление плоской многослойной стенки равно сумме термических сопротивлений отдельных слоев стенки при условии, что слои плотно прилегают друг к другу. Внутри каждого слоя линия изменения температуры (рис. 7.4) – прямая, но для многослойной стенки в целом она представляет собой ломаную линию.

Рисунок 7.5 – К выводу уравнения теплопроводности цилиндрической стенки

Теплопроводность цилиндрической стенки. В однородной цилиндрической стенке длиной L (рис. 7.5) температура в случае одномерного стационарного поля изменяется только в радиальном направлении, поэтому для поверхности произвольного радиуса r уравнение Фурье можно представить в виде

. (7.29)

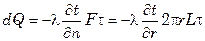
Для кольцевого слоя с радиусом r и толщиной dr, выделенного внутри стенки (рис. 7.5), при внутреннем и наружном радиусах соответственно r₁ и r₂ и температурах на внутренней и наружной поверхностях стенки и , согласно уравнению (7.29) имеем:

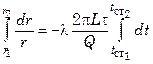
В результате интегрирования последнего выражения получим:

(7.30)

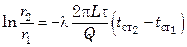
либо .

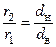
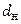
Если учесть, что ( и – наружный и внутренний диаметры цилиндра соответственно), то:

. (7.31)

Уравнения (7.30) и (7.31) являются уравнениями теплопроводности цилиндрической стенки при установившемся процессе теплообмена. Они показывают, что по толщине цилиндрической стенки (в отличие от плоской) температура изменяется криволинейно – по логарифмическому закону. При этом влияние кривизны стенки учитывается коэффициентом кривизныφ, значение которого определяется отношением диаметров . При


Рисунок 7.6 – Теплопроводность многослойной цилиндрической стенки	Рисунок 7.7 – К выводу уравнения теплопроводности сферической стенки

В соответствии с законом Фурье количество тепла, проходящее через шаровой слой толщиной dr и радиусом r

. (7.34)

В результате разделения переменных и интегрирования этого выражения в соответствующих пределах, получим:

, (7.35)

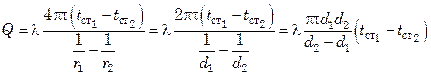
где и – диаметры внутренней и внешней поверхности соответственно.

Уравнения (7.35) являются расчетными формулами теплопроводности сферической стенки. Как следует из них, при 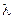= сonst температура в сферической стенке меняется по закону гиперболы.

По аналогии с плоской и цилиндрической стенками для многослойной сферической стенки

. (7.36)

Тепловое излучение

В тепловых процессах одновременно с теплопроводностью и конвекцией почти всегда наблюдается и тепловое излучение, причем, чем выше температура тела, отдающего тепло, тем большее количество тепла передается в виде лучистой энергии.

Тепловое излучение представляет собой процесс распространения внутренней энергии излучающего тела путем электромагнитных волн. При поглощении электромагнитных волн какими-либо другими телами они вновь превращаются в энергию теплового движения молекул. Источниками электромагнитных волн являются заряженные материальные частицы, т.е. электроны и ионы, входящие в состав вещества. По своей природе тепловое излучение аналогично излучению света, оба они представляют собой один вид энергии – лучистой – и подчиняются одним и тем же законам отражения, преломления и поглощения. Соответственно этому тепловое излучение характеризуется длиной волны. Однако в отличие от видимых световых лучей, имеющих длину волн 0,4÷0,8 мкм, длина волн теплового излучения лежит в основном в невидимой (инфракрасной) части спектра и составляет 0,8÷40 мкм.

Все тела излучают и поглощают лучистую энергию непрерывно. Интенсивность излучения зависит от природы тела, его температуры, длины волны, состояния поверхности, а для газов – еще от толщины слоя и давления. Твердые и жидкие тела имеют значительные поглощательную и излучательную способности. Вследствие этого в процессах лучистого теплообмена участвуют лишь тонкие поверхностные слои. Поэтому в этих случаях тепловое излучение приближенно можно рассматривать как поверхностное явление. Газы и пары характеризуются объемным характером излучения, в котором участвуют все частицы объема вещества. Излучение всех тел зависит от температуры. С увеличением температуры тела его энергия излучения увеличивается, так как увеличивается внутренняя энергия тела. При этом изменяется не только значение этой энергии, но и спектральный состав. При увеличении температуры повышается интенсивность коротковолнового излучения и уменьшается интенсивность длинноволнового излучения. В процессах излучения зависимость от температуры значительно большая, чем в процессах теплопроводности и конвекции. Вследствие этого при высоких температурах основным видом переноса тепла может быть тепловое излучение.

Лучистая энергия распространяется в однородной и изотропной среде прямолинейно. В отличие от теплопроводности и конвекции, лучистый теплообмен происходит не только между соприкасающимися, но и между удаленными друг от друга телами. Поток лучей, испускаемый нагретым телом, попадая на поверхность другого лучеиспускающего тела, частично поглощается, частично отражается (при этом угол падения равен углу отражения) и частично проходит сквозь тело без изменений, т.е.

; (7.37)

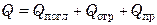
то есть ,

где – общая энергия падающих на тело лучей; – энергия, поглощенная телом; – энергия, отраженная от поверхности тела; – энергия лучей, проходящих сквозь тело без изменений.

Таким образом, отношения , и характеризуют поглощательную, отражательную и пропускательную способности тела. Если тело полностью поглощает падающую на него лучистую энергию, т.е. , а и равны нулю, то оно носит название абсолютно черного. При полном отражении телом лучистой энергии, , а , такие тела называют абсолютно белыми. Наконец, если тело пропускает все падающие на него лучи, не поглощая их и не отражая, , а , его называют абсолютно прозрачным или диатермичным.

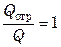
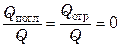
В природе не существует абсолютно черных, абсолютно белых и абсолютно прозрачных тел. Все тела в той или иной степени поглощают, отражают и пропускают сквозь себя падающие на них лучи, т.е. являются серыми. Однако твердые тела и жидкости практически непрозрачны для тепловых лучей, а большинство газов, наоборот, диатермичны.

Основные законы излучения

Закон Стефана-Больцмана. Количество тепла, излучаемого единицей поверхности тела в единицу времени, называют лучеиспускательной способностью тела Е, Вт/м 2 :

. (7.38)

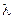
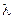
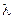
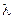
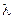
Как указывалось ранее, энергия излучения зависит от длины волн и температуры Т. Характеристикой энергии излучения по длинам волн служит интенсивность излучения I – лучеиспускательная способность тела в интервале длин волн от до + d , отнесенная к этому интервалу d , т.е.

. (7.39)

Лучеиспускательная способность тела E является интегральной характеристикой, которая учитывает энергию излучения волн всех длин от λ = 0 до λ = ∞.

. (7.40)

На основании электромагнитной теории света Планком аналитически была определена функциональная зависимость интенсивности излучения I₀ от температуры и длины волн для абсолютно черного тела. Согласно этой зависимости

, (7.41)

где c₁ – константа, равная 3,74∙10 –16 Вт/м 2 ; с₂ – константа, равная 1,44∙10 –2 (м∙К).

Интегрирование выражения (7.40) с учетом (7.41) дает зависимость для определения лучеиспускательной способности абсолютно черного тела Е₀:

, (7.42)

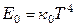
где к₀ – константа излучения абсолютно черного тела,
к₀ = 5,67∙10 –8 Вт/(м 2 ∙К 4 ).

Зависимость (7.42) носит название закона Стефана–Больцмана, так как была найдена экспериментально Стефаном и подтверждена Больцманом до того, как Планк вывел соотношение (7.41).

Таким образом, согласно закону Стефана–Больцмана, лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры.

При проведении технических расчетов выражение (7.42) удобнее использовать в виде

, (7.43)

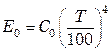
где С₀ – коэффициент излучения абсолютно черного тела, равный С₀ = k₀∙10 8 = 5,67 Вт/(м 2 ∙К 4 ).

Исследования показали, что закон Стефана-Больцмана применим не только к абсолютно черным телам, но и к серым. В этом случае его записывают в виде

(7.44)

(C по аналогии с абсолютно черным телом называют коэффициентом излучения серых тел).

Отношение коэффициентов излучения данного тела и абсолютно черного С/С₀ = e носит название относительной излучательной способности или степени черноты данного тела. С учетом этого понятия закон Стефана-Больцмана принимает вид

. (7.45)

Рисунок 7.8 – К выводу закона Кирхгофа

Закон Кирхгофа устанавливает соотношение между лучеиспускательной и поглощательной способностями тел. Это соотношение может быть получено из рассмотрения процесса обмена лучистой энергией между абсолютно черным и серым телами (рис. 7.8).

Поверхности рассматриваемых тел параллельны и расположены на расстоянии, при котором излучение каждого из тел попадает на другое. Абсолютно черное тело имеет температуру T₀, лучеиспускательную способность E₀ и поглощательную A₀ = 1, серое тело имеет соответственно Т, Е и А, при этом Т > T₀. Излучение Е попадает на абсолютно черное тело и целиком им поглощается. Излучение E₀ попадает на серое тело. При этом часть этого излучения, равная E₀А, поглощается, а другая часть, равная E₀(1 – А), отражается на абсолютно черное тело и поглощается им. В результате этого обмена абсолютно черное тело получает суммарное количество энергии:

. (7.46)

При выравнивании температур обоих тел наступает тепловое равновесие, при котором Q = 0, т.е. . Следовательно,

. (7.47)

Последнее соотношение является математическим выражением закона Кирхгофа, согласно которому отношение лучеиспускательной способности тел к их поглощательной способности для всех тел одинаково, равно лучеиспускательной способности абсолютно черного тела при той же температуре и зависит только от температуры.

В результате подстановки значений E и E₀ из равенств (7.44) и (7.45) в соотношение (7.47) получаем

. (7.48)

Рисунок 7.9 – К формулировке закона Ламберта

Так как , то , т.е. способность тела к поглощению излучения численно равна степени его черноты. Учитывая, что e и A изменяются в пределах от 0 до 1, из равенства (7.47) следует, что лучеиспускательная способность реального тела всегда меньше лучеиспускательной способности абсолютно черного тела при той же температуре.

Закон Ламбертаопределяет изменение интенсивности излучения по различным направлениям. Согласно этому закону излучение энергии элементом поверхности в направлении элемента (рис. 7.9) пропорционально излучению dQ (по направлению нормали к ), телесному углу dψ (под которым виден элемент из элемента ) и косинусу угла φ, образованного прямой, соединяющей элементы и , и нормалью к элементу .