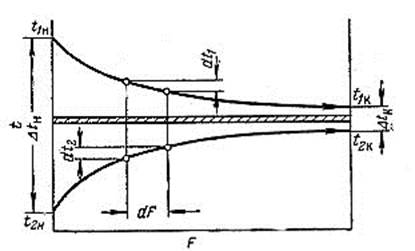
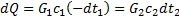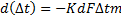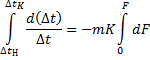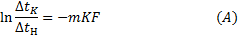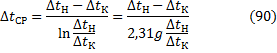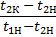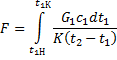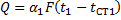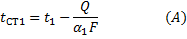Уравнение теплопередачи при прямотоке и противотоке теплоносителей (8 видео)

Уравнение теплопередачи при прямотоке и противотоке теплоносителей.

Пусть с одной стороны стенки (рис. 17) движется с массовой скоростью G₁ более нагретый теплоноситель, имеющий теплоемкость c₁.

Рис. 17. Изменение температуры теплоносителей при параллельном токе.

С другой стороны стенки в том же направлении движется более холодный теплоноситель, массовая скорость которого равна G₂, а теплоемкость с₂. Допустим, что теплоемкости постоянны и теплообмен между движущимися прямотоком теплоносителями происходит только через разделяющую их стенку (поверхностью F). Процесс теплопередачи является установившимся, или непрерывным.

По мере протекания теплоносителей вдоль стенки их температуры будут изменяться вследствие теплообмена. Соответственно будет меняться и разность температур At между теплоносителями.

На элементе поверхности теплообмена dF (см. рис. 17) более нагретый теплоноситель охлаждается на dt₁ град, а более холодный нагревается на dt₂ град. Уравнение теплового баланса для элемента поверхности dF имеет вид

W₁ и W₂— водяные эквиваленты теплоносителей (см. стр. 262),

Знак «минус» указывает на охлаждение более нагретого теплоносителя в процессе теплообмена. Следовательно

Складывая эти выражения и обозначая 1/W₁ + 1/W₂ = т, получим

Вместе с тем dQ = KdF t, поэтому

Разделяем переменные и интегрируем полученное выражение в пределах изменения t вдоль всей поверхности теплообмена от t_1Н— t₂_H = t_Н до t₁_K— t₂_K = t_K и dF — от 0 до F. При этом принимаем коэффициент теплопередачи К величиной постоянной.

где — начальная разность температур (на одном конце теплообменника); — конечная разность температур (на противоположном конце теплообменника).

Уравнение теплового баланса для всей поверхности теплообмена

Подставив значение m в уравнение (А), получим

Сопоставляя выражение для Q, полученное при постоянных значениях К, W₁ и W₂ вдоль поверхности теплообмена, с основным уравнением теплопередачи (5), заключаем, что средняя движущая сила, или средний температурный напор, представляет собой среднюю логарифмическую разность температур:

Уравнение (89) является уравнением теплопередачи при прямотоке теплоносителей. С помощью уравнения (89) по заданной тепловой нагрузке Q и известным начальным и конечным температурам теплоносителей определяется основная расчетная величина — поверхность теплообмена.

Из уравнения (А) следует, что

Следовательно, при прямотоке температуры теплоносителей изменяются по асимптотически сближающимся кривым. Если бы температуры теплоносителей изменялись прямолинейно вдоль поверхности теплообмена, то средний температурный напор выражался бы среднеарифметической разностью температур.

При отношении разности температур теплоносителей на концах теплообменника ( / )

Графики для нахождения значения поправочного множителя f, а также уравнения для аналитического определения средней разности температур (в тех случаях, когда требуется более точное вычисление ) приводятся в справочной и специальной литературе.

Следует отметить, что все приведенные выше выражения для средней движущей силы , в том числе для прямотока и противотока, получены исходя из предположения о движении потоков в режиме идеального вытеснения, т. е. при допущении, что все частицы движутся параллельно с одинаковыми скоростями, не перемешиваясь друг с другом.

Для уточнения расчета следовало бы учитывать влияние перемешивания на среднюю движущую силу процесса теплообмена.

Допустим, что в режиме идеального вытеснения (рис. 19) изменение температуры более холодного теплоносителя вдоль поверхности теплообмена происходит по кривой от t’_2Н до t₂_K, температура более горячего теплоносители t₁ = const (например, при обогреве насыщенным водяным паром).

Рис. 19. Влияние перемешивания на среднюю движущую силу процесса теплообмена.

В другом предельном случае — режиме идеального смешения — температура более холодного теплоносителя вдоль поверхности теплообмена постоянна и равна его конечной температуре: t’’_2Н=t₂_K=const.

В большинстве случаев распределение температур является промежуточным между указанными предельными условиями и температура более холодного теплоносителя изменяется от t_2Н до t₂_K, причем t’’_2Н > t_2Н > t’_2Н.

Таким образом, в любой точке поверхности теплообмена движущая сила, определяемая вертикальным отрезком между t₁ и линией изменения температур нагреваемой жидкости, и соответственно будут меньше, чем при идеальном вытеснении, или поршневом потоке, и больше, чем при идеальном смешении (например, для точки А на рис. 19 a’b>ab>a’’b). Однако для процессов теплопередачи методика расчета с учетом структуры потоков (по данным кривых отклика, см. стр. 119) еще недостаточно разработана.

При выводе формул для расчета допускалось также, что коэффициент теплопередачи К и теплоемкости с обоих теплоносителей не изменяются с изменением температуры. В тех случаях, когда величины К и с изменяются в данном интервале температур более чем в 2—3 раза, для более точного расчета поверхности теплообмена используют метод графического интегрирования (рис. 20).

Рис. 20. К расчету поверхности теплообмена методом графического интегрирования.

Для элементарного участка поверхности теплообмена (dF) величина К может быть принята постоянной. Тогда уравнение теплопередачи в дифференциальной форме для более нагретого теплоносителя будет иметь вид

и поверхность теплообмена

где t₁ и t₂ — текущие температуры более нагретого и более холодного теплоносителя соответственно; t_1Н и t₁_K — начальная и конечная температуры более нагретого теплоносителя.

Принимая ряд промежуточных значений t₁ в пределах от t₁_Н до t₁_K, для каждой из этих температур находят значения с, К и определяют, пользуясь уравнением теплового

баланса, температуру t₂. Строя зависимость от t (рис. 20), получают кривую АВ, площадь под которой, ограниченная ординатами, соответствующими t_1Н и t₁_K, выражает в масштабе поверхность теплообмена F. Аналогичный расчет может быть проведен для более холодного теплоносителя.

Выбор взаимного направления движения теплоносителей.Правильный выбор взаимного направления движения теплоносителей имеет существенное значение для наиболее экономичного проведения процессов теплообмена.

Для сравнительной оценки прямотока и противотока сопоставим эти виды взаимного направления движения теплоносителей с точки зрения расхода теплоносителей и средней разности температур.

В случае прямотока (рис. 21) конечная температура более холодного теплоносителя t₂_K не может быть выше конечной температуры более нагретого теплоносителя t₁_K

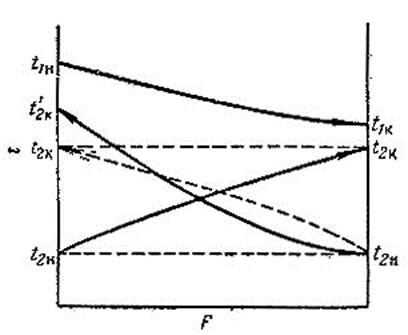Уравнение теплопередачи при прямотоке и противотоке теплоносителей

Рис. 21. Сравнение прямотока и противотока теплоносителей.

Практически для осуществления процесса теплообмена на выходе из теплообменника должна быть некоторая разность температур

При противотоке более холодный теплоноситель с той же начальной температурой t₂_H, что и при прямотоке, может нагреться до более высокой температуры t’₂_K, близкой к начальной температуре t_1Н более нагретого теплоносителя. Это позволяет сократить расход более холодного теплоносителя, но одновременно приводит к некоторому уменьшению средней разности температур и соответственно — к увеличению потребной поверхности теплообмена при противотоке по сравнению с прямотоком. Однако экономический эффект, достигаемый вследствие уменьшения расхода теплоносителя при противотоке, превышает дополнительные затраты, связанные с увеличением размеров теплообменника. Отсюда следует, что применение противотока при теплообмене более экономично, чем прямотока.

Теперь сопоставим противоток с прямотоком при одних и тех же начальных и конечных температурах теплоносителей. Изменение температуры более холодного теплоносителя показано на рис. 21 пунктиром. Расчеты показывают, что в данном случае средняя разность температур при противотоке будет больше, чем при прямотоке, а расход теплоносителей одинаков. Следовательно, скорость теплообмена при противотоке будет больше, что и обусловливает преимущество противотока перед прямотоком.

Вместе с тем в отдельных случаях выбор направления движения теплоносителей прямотоком диктуется технологическими соображениями. Так, в барабанных сушилках (см. главу XV) высушиваемый материал и греющий агент (топочные газы, нагретый воздух) направляют параллельным током с тем, чтобы не подвергать перегреву высушенный материал во избежание его окисления, осмоления и т. п.

Указанные выше преимущества противотока относятся к процессам теплообмена без изменения агрегатного состояния теплоносителей. Если температура одного из теплоносителей (например, конденсирующегося насыщенного пара) остается постоянной вдоль, поверхности теплообмена, а температура теплоносителя по другую сторону стенки изменяется или оба теплоносителя имеют постоянные температуры, не изменяющиеся во времени и вдоль поверхности теплообмена, то направление движения теплоносителей не оказывает влияния на разности их температур, среднюю разность температур и расходы теплоносителей.

Определение температуры стенок. Как видно из предыдущего, в ряде случаев определение коэффициента теплоотдачи а невозможно без знания температуры более нагретой поверхности стенки (t_СТ1) или температуры менее нагретой ее поверхности (t_СТ2).

Температуру стенки находят методом последовательных приближений: задавшись произвольно этой температурой, определяют а, рассчитывают К по формуле (83), а затем, по приводимым ниже формулам, проверяют сходимость рассчитанной величины t_Cr с предварительно принятой; расчет повторяют до близкого совпадения рассчитанного и принятого значений Us*

Расчет t_СТ1 и t_СТ2 производят исходя из уравнений теплоотдачи и теплопередачи.

Количество тепла, отдаваемое горячим теплоносителем

где F — поверхность теплообмена; t₁— температура горячего теплоносителя.

Количество тепла, получаемое холодным теплоносителем

где t₂ — температура холодного теплоносителя. Из этих уравнений теплоотдачи находим

Согласно общему уравнению теплопередачи (5)

где — средняя разность температур между теплоносителями.

Подставляя значение Q из уравнения теплопередачи в уравнения (А) и (Б) и сокращая F, окончательно получим

Содержание

Тепловой расчет теплообменных аппаратов
4 комментарий на « Тепловой расчет теплообменных аппаратов »
Теплопередача при изменяющихся температурах вдоль поверхности теплообмена
📺 Видео

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Тепловой расчет теплообменных аппаратов

Здравствуйте! Теплообменным аппаратом называется устройство, в котором осуществляется теплообмен между двумя или несколькими теплоносителями либо между теплоносителями и твердыми телами (насадкой, стенкой). Роль теплоносителя может выполнять и среда, окружающая аппарат. По своему назначению и конструктивному оформлению теплообменники могут быть самыми различными, начиная от простейшего (радиатор) и кончая наиболее совершенным (котельный агрегат). По принципу действия теплообменные аппараты подразделяются на рекуперативные, регенеративные и смесительные.

Рекуперативными называют аппараты, в которых одновременно протекают горячий и холодный теплоносители, разделенные между собой твердой стенкой. К числу таких аппаратов относятся подогреватели, котельные агрегаты, конденсаторы, выпарные аппараты и др.

Регенеративными называют аппараты, в которых одна и та же поверхность нагрева попеременно омывается то горячей, то холодной жидкостью. При этом теплота, аккумулированная стенками аппарата при их взаимодействии с горячей жидкостью, отдается холодной жидкости. Примером регенеративных аппаратов являются воздухоподогреватели мартеновских и доменных печей, отопительные печи и др. В регенераторах теплообмен всегда происходит в нестационарных условиях, тогда как рекуперативные аппараты большей частью работают при стационарном режиме.

Рекуперативные и регенеративные аппараты называют также поверхностными, так как процесс передачи теплоты в них неизбежно связан с поверхностью твердого тела.

Смесительными являются аппараты, в которых передача теплоты осуществляется при непосредственном смешивании горячей и холодной жидкости.

Взаимное движение теплоносителей в теплообменных аппаратах может быть различным (рис. 1.).

В зависимости от этого различают аппараты с прямоточным движением, противоточным движением, перекрестным током и со сложным направлением движения теплоносителей (смешанного тока). Если теплоносители протекают параллельно в одном направлении, то такая схема движения называется прямотоком (рис. 1.). При противотоке теплоносители движутся параллельно, но навстречу друг другу. Если направления движения жидкостей пересекаются, то схема движения называется перекрестным током. Кроме названных схем, на практике применяются и более сложные: одновременно прямоток и противоток , многократно перекрестный ток и др.

В зависимости от технологического назначения и конструктивных особенностей теплообменные аппараты подразделяются на водоподогреватели, конденсаторы, котельные агрегаты, испарители и др. Но общим является то, что все они служат для передачи теплоты от одного теплоносителя к другому, поэтому и основные положения теплового расчета для них одинаковы. Разница может состоять только в конечной цели расчета. При проектировании нового теплообменного аппарата задачей расчета является определение поверхности нагрева; при поверочном тепловом расчете имеющегося теплообменника требуется найти количество переданной теплоты и конечные температуры рабочих жидкостей.

В основу теплового расчета в обоих случаях положены уравнения теплового баланса и уравнение теплопередачи.

Уравнение теплового баланса теплообменного аппарата имеет вид:

где М — массовый расход теплоносителя, кг/с; cpm — удельная массовая изобарная средняя теплоемкость теплоносителя, Дж/(кг*°С).

Здесь и в дальнейшем индексом «1» обозначаются величины, относящиеся к горячей жидкости (первичный теплоноситель), а индексом «2» — к холодной жидкости (вторичный теплоноситель); штрих соответствует температуре жидкости на входе в аппарат, а два штриха — на выходе.

При расчете теплообменников часто пользуются понятием полной теплоемкости массового расхода теплоносителя (водяного эквивалента), равной С = Мср Вт/°С. Из выражения (1) следует, что

то есть отношение изменений температур однофазных теплоносителей обратно пропорционально отношению их полных расходных теплоемкостей (водяных эквивалентов).

Уравнение теплопередачи записывается так: Q=k*F*(t1—t2), где t1, t2— температуры первичного и вторичного теплоносителей; F — площадь поверхности теплопередачи.

При теплообмене в большинстве случаев изменяются температуры обоих теплоносителей и, следовательно, изменяется температурный напор Δt = t1—t2. Коэффициент теплопередачи по поверхности теплообмена также будет иметь переменную величину, поэтому в уравнение теплопередачи следует подставлять средние значения температурного напора Δtср и коэффициента теплопередачи kсp, то есть

Площадь теплообмена F рассчитывается по формуле (3), тепловая производительность Q при этом задается. Для решения задачи необходимо вычислить средний по всей поверхности коэффициент теплопередачи kсp и температурный напор Δtср.

При вычислении среднего температурного напора необходимо учитывать характер изменения температур теплоносителей вдоль поверхности теплообмена. Из теории теплопроводности известно, что в пластине или цилиндрическом стержне при наличии разности температур на торцах (боковые поверхности изолированы) распределение температур по длине линейное. Если же на боковой поверхности имеет место теплообмен или система располагает внутренними источниками теплоты, то распределение температур является криволинейным. При равномерном распределении источников теплоты изменение температур по длине будет параболическим.

Таким образом, в теплообменных аппаратах характер изменения температур теплоносителей отличается от линейного и определяется полными теплоемкостями С1 и С2 массовых расходов теплоносителей и направлением их взаимного движения (рис. 2).

Из графиков видно, что изменение температуры вдоль поверхности F неодинаково. В соответствии с уравнением (2) большее изменение температуры будет у теплоносителя с меньшей теплоемкостью массового расхода. Если же теплоносители одинаковы, например, в водоводяном теплообменнике, то характер изменения температур теплоносителей будет всецело определяться их расходами, причем при меньшем расходе изменение температур будет большим. При прямотоке конечная температура t»2 нагреваемой среды всегда меньше температуры t»1 греющей среды на выходе из аппарата, а при противотоке конечная температура t»2 может быть выше температуры t»1 (см. для противотока случай, когда C1 > C2). Следовательно, при одинаковой начальной температуре нагреваемую среду при противотоке можно нагреть до более высокой температуры, чем при прямотоке.

При прямотоке температурный напор вдоль поверхности нагрева изменяется в большей степени, чем при противотоке. Вместе с тем среднее его значение в последнем случае больше, вследствие чего поверхность нагрева аппарата с противотоком будет меньшей. Таким образом, при равных условиях в этом случае будет передано большее количество теплоты. Исходя из этого, предпочтение следует отдавать аппаратам с противотоком.

В результате аналитического исследования теплообменного аппарата, работающего по схеме прямотока, установлено, что температурный напор вдоль поверхности теплообмена изменяется по экспоненциальному закону, поэтому средний температурный напор может быть вычислен по формуле:

где Δtб — большая разность температур между горячим и холодным теплоносителем (с одного края теплообменника); Δtм — меньшая разность температур (с другого края теплообменника).

При прямотоке Δtб = t’1 — t’2 и Δtм = t»1 — t»2 (рис. 2.). Эта формула справедлива также и для противотока с той лишь разницей, что для случая, когда С1 С2 Δtб = t»1 — t’2 и Δtм = t’1 — t»2.

Средняя разность температур между двумя средами, вычисляемая по формуле (4), называется среднелогарифмическим. температурным напором. Вид выражения обусловлен характером изменения температур вдоль поверхности нагрева (криволинейная зависимость). Если бы зависимость была линейной, то следовало бы определять температурный напор как среднеарифметический (рис. 3.). Значение среднеарифметического напора Δtа.ср всегда больше среднелогарифмического Δtл.ср. Однако в тех случаях, когда температурный напор по длине теплообменника изменяется незначительно, то есть выполняется условие Δtб/ Δtм

Осреднение температурного напора для аппаратов с перекрестным и смешанным током отличается сложностью расчетов, поэтому для ряда наиболее употребительных схем результаты решений обычно приводятся в виде графиков. Исп. литература: 1) Основы теплоэнергетики, А.М. Литвин, Госэнергоиздат, 1958. 2)Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976. 3) Теплотехника, изд.2, под общей ред. И.Н.Сушкина, Москва «Металлургия», 1973.

Видео:Теплопередача. Виды теплопередачи | Физика 8 класс #2 | ИнфоурокСкачать

4 комментарий на « Тепловой расчет теплообменных аппаратов »

столкнулся с такой практической задачей: в комнате 4 радиатора отопления, подключены по двухтрубной системе. Оплата за тепло по квартирному теплосчетчику.

Если включить все четыре батареи на полную мощность, то будет слишком жарко. Практика показывает, что для оптимальной температуры надо включить или 2 батареи на полную, а 2 выключить; или включить все четыре на минимальный обогрев.

Как вы думаете, в каком случае затраты на обогрев будут меньше?

Игорь, сведите все к простой математике. Чем больше теплосъем, тем больше оплата за отопление. И наоборот, чем меньше теплосъем, тем меньше оплата за отопление. Формула потребленного тепла выглядит как Q=G*c*(T1-T2), где Q=ккал/сек, с- это теплоемкость воды = 1 ккал/(кг*градус), Т1 — температура в подаче в градусах, Т2 — температура в обратке в градусах, G — количество теплоносителя в кг/сек. Если умножить результат на 3600, то получите результат в часах. По своему теплосчетчику вы можете узнать количество теплоносителя, который прошел через ваши батареи, а так же температуру прямой и обратной трубы. Путем регулирования своих 4х батарей вы можете по количеству теплоносителя регулировать стоимость потребленного тепла. Как-то так.

Подскажите пожалуйста, если в частном доме с центральным отоплением поставить теплообменник, то за отопление придется платить столько же сколько без него? Прибора учета нет.

Если прибора учета нет, то будете платить столько же, сколько и до установки теплообменника

Видео:Теплопроводность, конвекция, излучение. 8 класс.Скачать

Теплопередача при изменяющихся температурах вдоль поверхности теплообмена

В теплообменных аппаратах и теплоиспользующих устройствах температура греющего и нагреваемого теплоносителей изменяются вдоль поверхности теплообмена: температура греющего теплоносителя понижается, а температура нагреваемого повышается. Исключение составляют теплообменные аппараты, в которых с одной стороны поверхности испаряется жидкость или конденсируется пар(например испарители или конденсаторы).

В условиях изменяющихся температур теплоносителей уравнение теплопередачи можно записать в следующем виде:

, (217)

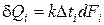
Тепловой поток передаваемый через всю поверхность теплообмена при постоянном коэффициенте теплопередачи k равен

(218)

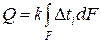
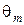
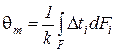
Для учета изменения температур теплоносителей по поверхности теплообмена в расчетное уравнение теплопередачи вводится средняя разность температур (средний температурный напор) , который определяется уравнением

, (219)

где 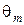— средняя разность температур.

Из сопоставления уравнений 218 и 219 следует

(220)

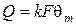
Уравнение 220 называют уравнением теплопередачи для теплообменных аппаратов (обобщенное уравнение теплопередачи)

Вид расчетного соотношения для средней разности температур (219) существенно зависит от взаимного направления греющего и нагреваемого теплоносителей. Различают следующие направления движения теплоносителей в рекуперативных теплообменниках: прямоток, противоток, перекрестный ток, смешанный ток.

На рис. 25 показаны схемы движения теплоносителей и изменение температур теплоносителей при прямотоке и противотоке.

Рис. 25. График изменения температуры теплоносителей

при прямотоке (а) и противотоке (б)

В процессе теплообмена греющий теплоноситель отдает некоторое количество теплоты (Q₁), нагреваемый теплоноситель получает такое же количество теплоты (Q₂) (теоретический процесс, без потерь теплоты в окружающую среду). Пренебрегая падением давления теплоносителей при движении, т.е. считая процесс протекающим изобарным, из первого начала термодинамики имеем

, (221)

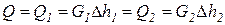
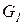
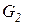
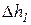
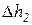
где Q – мощность теплообменного аппарата, Вт; и – расход горячего и холодного теплоносителей соответственно, кгс; и – удельное изменение энтальпии греющего и нагреваемого теплоносителей соответственно, Джкг.

Для конвективных теплообменных аппаратов (в процессе теплообмена отсутствуют фазовые переходы) в силу того, что имеем

, (222)

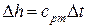
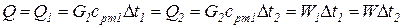
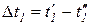
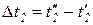
где c_pm₁ и c_pm₂ – средние теплоемкости горячего и холодного теплоносителей; W₁=G₁c_pm₁ и W₂=G₂c_pm₂ – водяные эквиваленты горячего и холодного теплоносителей; ; (рис. 25).

Уравнения (221 и 222) называются уравнениями теплового баланса теплообменного аппарата (ТА).

В силу того, что для теоретического процесса теплопередачи в ТА, тепловой поток определенный из уравнение теплового баланса (222) равен тепловому потоку определенному по уравнению теплопередачи (220) имеем

(223)

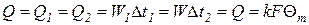
Расчетные соотношения для определения средней разности температур простейших схем взаимного движения теплоносителя: прямотока и противотока (рис. 25) получаются из выражения (223) записанного для элементарного участка теплообмена

, (224)

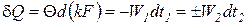
где 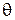– текущая средняя разность температур (текущий температурный напор).

Знаки в уравнении элементарного теплового потока (224) определяются принятым направлением движения теплоносителей: верхние знаки относятся к прямотоку, а нижние – к противотоку.

Выделим из исходного дифференциального уравнения (224) изменения температуры для горячего и холодного теплоносителей

(224а)

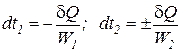
Выразим разность изменения температур горячего и холодного теплоносителей

, (224б)

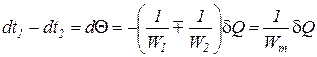
где W_m – приведенный водяной эквивалент обоих потоков, .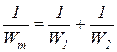

Окончательно имеем следующее преобразованное выражение теплопередачи на элементарном участке

(225)

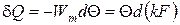
Разделив переменные в уравнении (225) и его проинтегрировав получим первое интегральное уравнение

. (226)

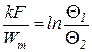
Второе интегральное уравнение получается при непосредственном интегрировании уравнения теплопередачи (225)

(227)

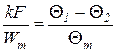
Сопоставляя уравнения (226 и 227) получим расчетное уравнение для средней разности температур

, (228)

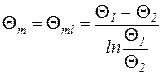
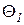
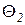
где и — начальная и конечная разности температур соответственно.

Расчетное уравнение средней разности температур (228), справедливое для схем прямотока и противотока, называется среднелогарифмической разностью температур или уравнением Грасгофа.

Начальная и конечная разность температур для схемы прямотока и противотока определяются по следующим соотношения (рис. 25):

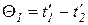
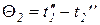
для схемы прямоток ; , (228а)

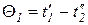
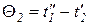
для схемы противоток ; (228б)

При незначительном изменении температуры теплоносителей вдоль поверхностей теплообмена вместо среднелогарифмической разности температур можно пользоваться среднеарифметической разностью температур

(229)

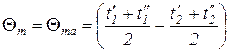
Среднеарифметическая разность температур всегда больше среднелогарифмической, но при 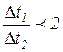они отличаются друг от друга менее 3%, что вполне допустимо в технических расчетах.

Точное определение среднелогарифмической разности температур для схем с перекрестным и смешанным током теплоносителей связано с большими трудностями. В этом случае удобно пользоваться расчетными графиками, составленными для наиболее распространенных схем теплообменных аппаратов [2, 3, 8, 9].

Предварительно по формуле Грасгофа (228) одсчитывается среднелогарифмическая разность температур для противоточного теплообменного аппарата. Затем вычисляются вспомогательные характеристики R и PS по уравнениям

, . (230)

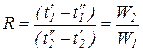
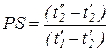
По значениям этих характеристик с учетом схемы движения теплоносителей (число ходов по трубному и межтрубному пространству) из графиков определяется коэффициент e_D_t (рис. 3, 4, 5) [2, 3, 8, 9].

Действительная средняя разность температур между теплоносителями для рекуперативных ТА всех типов определяется по соотношению

, (231)

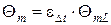
где e_D_t – коэффициент, учитывающий различие между действительной средней разностью температур (Q_m) и средней логарифмической разностью температур между теплоносителями при противоточной схеме движения теплоносителей (Q_mL).