Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).
Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

Алгоритм решения простейших уравнений с тангенсом
Давайте с вами рассмотрим типичное уравнение, например, (tgx=sqrt).
Пример. Решить уравнение (tgx=sqrt).
Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…
…и обозначим то место на оси, куда мы должны попасть в итоге.
Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.
Точки найдены. Давайте подпишем значение одной из них…
…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac+πn), (n∈Z).
Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn), (n∈Z).
Пример. Решить уравнение (tgx=-1).
Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:
Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.
Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.
Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.
Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.
Видео:10 класс, 20 урок, Функции y=tgx, y=ctgx, их свойства и графикиСкачать

Алгоритм решения простейших уравнений с котангенсом
Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.
Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac<sqrt>) на оси котангенсов?
Строим круг, проводим нужные оси.
Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…
…и соединяем центр окружности и точку на оси котангенсов прямой линией.
По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…
…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).
Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt), котангенс будет (frac<sqrt>).
Разберем еще пример, а потом подведем итог.
Пример. Решить уравнение (ctgx=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.
Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:
Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.
Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.
Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.
Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.
Видео:Решение уравнений вида tg x = a и ctg x = aСкачать

Простейшие тригонометрические уравнения. Часть 1
Простейшими называются тригонометрические уравнения следующих четырёх видов:
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.
Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.
Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.
Видео:Алгебра 10 класс (Урок№43 - Уравнение tg x=a.)Скачать

Уравнения и
Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.
Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .
Абитуриент, будь внимателен! Уравнения или решений не имеют!
Начнём с самых простых уравнений.
. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:

Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :
Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :
И записываем ответ:
Обсуждать тут уже нечего, не так ли? 🙂
Можете, кстати, записать ответ и в другом виде:
Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
На тригонометрическом круге имеются две точки с ординатой 0:
Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:
Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):
Теперь мы можем сделать и второе полезное наблюдение.
Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .
Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.
Имеем вертикальную пару точек с абсциссой :
Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):
Аналогично, все углы, соответствующие нижней точке, описываются формулой:
Обе серии решений можно описать одной формулой:
Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
Имеем горизонтальную пару точек с ординатой :
Углы, отвечающие правой точке:
Углы, отвечающие левой точке:
Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:
Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то
Мы получили первую серию решений . А если — нечетно, , то
Это вторая серия .
Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .
Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
На этом с синусом и косинусом пока всё. Переходим к тангенсу.
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).
Из подобия треугольников и имеем:
Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.
Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Уравнение
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .
.
Имеем диаметральную горизонтальную пару точек:

Эта пара, как мы уже знаем, описывается формулой:
Имеем диаметральную пару:
Вспоминаем второе полезное наблюдение и пишем ответ:
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
На этом заканчиваем пока и с тангенсом.
Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;
при уравнение равносильно уравнению .
Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂
Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.
А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Математика. Уравнения tg х = а и ctg х = а . Примеры.
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале только один корень. Если , то корень заключён в промежутке ; если а Просмотр содержимого документа
«Математика. Уравнения tg х = а и ctg х = а . Примеры.»
🌟 Видео
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Решить неравенство tg xСкачать
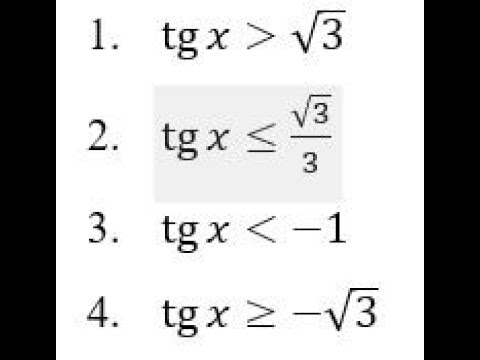
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Катеты равны 9^x и 6^x, а гипотенуза равна 4^x ➜ Найдите xСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

10 Функции y=tgx и y=ctgxСкачать
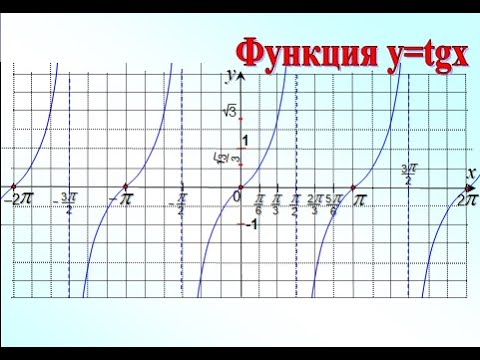
Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Что такое синус, косинус, тангенс и котангенс объяснениеСкачать

12 часов Тригонометрии с 0.Скачать

Решение простейших тригонометрических уравнений tgx=a и ctgx=aСкачать

10 класс, 13 урок, Синус и косинус Тангенс и котангенсСкачать

Решите уравнение ★ tg(ctgx)=ctg(tgx) ★ Быстрый способСкачать

Тригонометрия, Урок 4, Тангенс и Котангенс.Скачать









































