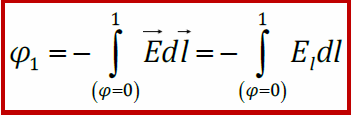
Элементарная работа поля 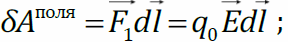

Градие́нт —вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины 
Потенциал – непрерывная функция координат! График потенциала никогда не имеет разрывов.
Методы расчёта потенциала электростатического поля: метод суперпозиий и интегральная связь Еи φ.
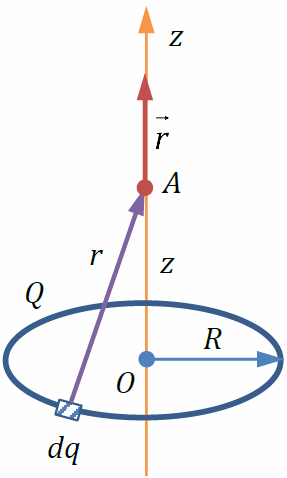
По тонкому кольцу равномерно распределён заряд Q > 0 . Пусть потенциал равен нулю в бесконечно удалённой точке. Разобьём кольцо на малые участки с зарядами dqи воспользуемся методом суперпозиций: 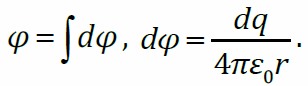


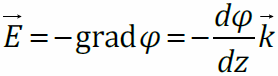
Этот же результат можно получить методом суперпозиции (билет №2)
Потенциал электростатического поля. Связь между напряженностью поля и потенциалом (интегральная и дифференциальная). Примеры расчета потенциала электростатического поля. Диполь в электростатическом поле.
Потенциалом электростатического поля [φ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.

Дата добавления: 2016-07-05 ; просмотров: 7881 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Лекция 6
- 1.13.Потенциал системы точечных зарядов.
- 2.14. Потенциал заряженного тела.
- 3.15.Измерение разности потенциалов.
- 4.16.Понятие скалярного поля
- 5.17.Градиент скалярного поля в различных системах координат.
- 6.18.Связь напряженности и потенциала.
- 7.19.Эквипотенциальные поверхности
- 8.20.Примеры
- Связь между напряженностью поля и потенциалом. Эквипотенциальные поверхности и силовые линии.
- 📸 Видео
Видео:Физика. Связь напряженности и потенциалаСкачать

Лекция 6
Видео:Билет №03 "Потенциал"Скачать

1.13.Потенциал системы точечных зарядов.
Потенциал, как и напряженность, подчиняется принципу суперпозиции.
Видео:Связь напряженности и потенциала. ЭлектростатикаСкачать

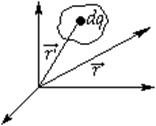
2.14. Потенциал заряженного тела.
Видео:Связь между потенциалом и напряжённостью в однородном электрическом полеСкачать

3.15.Измерение разности потенциалов.
Производится при помощи электрометров и пламенных зондов.
Видео:Билет №04 "Потенциал электростатического поля"Скачать

4.16.Понятие скалярного поля
Если в пространстве каждой точке поставлено в соответствие некоторое число, то говорят, что определено скалярное поле
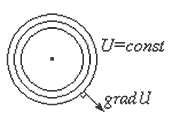
Если соединить точки с одинаковым значением функции, то получим поверхность u(x,y,z)=const, которая называется поверхностью уровня. Таким образом, скалярное поле характеризуется поверхностями уровня, в отличие от векторного поля, которое характеризуется силовыми линиями. Векторное поле существенно сложнее скалярного, т.к. имеет такие особенности, как источники, стоки и завихренности. Поверхности уровня не касаются и не пересекаются.
Векторное поле характеризуется двумя дифференциальными операторами, а скалярное поле одним — градиентом.
Для скалярного поля нас может интересовать, в каком направлении оно изменяется и как быстро это происходит, т.е. вектор. Этот вектор и называется градиентом.
 | Градиентом скалярной функции называется вектор, направленный в сторону максимального возрастания функции, а модуль его равен производной функции в данном направлении.
|
Очевидно, что градиент и поверхность уровня перпендикулярны друг другу.
Видео:Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

5.17.Градиент скалярного поля в различных системах координат.
В декартовой
В цилиндрической
В сферической
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

6.18.Связь напряженности и потенциала.
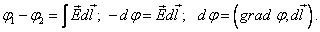
Таким образом, напряженность показывает направление наибольшего убывания потенциала. Это дифференциальная связь между напряженностью и потенциалом. Она справедлива только в электростатике.
Видео:Связь между напряженностью электростатического поля и напряжением | Физика 10 класс #51 | ИнфоурокСкачать

7.19.Эквипотенциальные поверхности
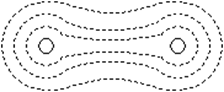
Если речь идет об электрическом поле, то поверхности одинакового уровня (одинакового потенциала) называют эквипотенциальными поверхностями. Они перпендикулярны (ортогональны) линиям напряженности. Следовательно, зная одно, можно изобразить и другое.
Пример: точечный заряд, пара разноименных, пара одноименных.
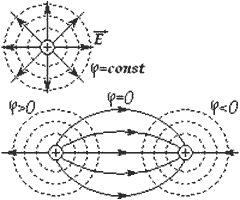
Для проводников в электростатике эквипотенциальная поверхность вырождается в эквипотенциальный объём.
Видео:Связь между напряженностью и потенциалом. 2021-6Скачать

8.20.Примеры
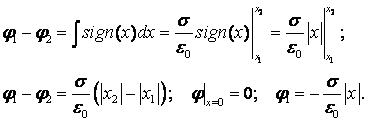
Пример 1:Потенциал плоскости
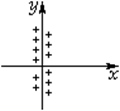
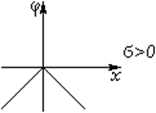

Пример 2: Потенциал двух бесконечных разноименно заряженных плоскостей.
Видео:3.1.6 Связь между напряженностью и разностью потенциаловСкачать
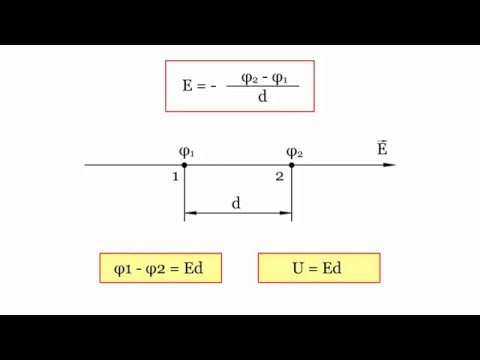
Связь между напряженностью поля и потенциалом. Эквипотенциальные поверхности и силовые линии.
Читайте также:
|
 |
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА.
Электрический конденсатор – пассивный электронный компонент, обычно двухполюсник с определённой величиной ёмкости и малой омической проводимостью. Служит для накопления заряда и энергии электрического поля. Выполняется, как правило, в виде двух электродов в форме пластин, разделённых диэлектриком малой толщины.
В цепи постоянного тока конденсатор проводит ток только в момент включения его в цепь, после окончания переходного процесса ток через него уже не протекает. В цепях переменного тока прохождение колебаний переменного тока обусловлено процессом циклической перезарядки конденсатора, замыкаясь током смещения.
Способность конденсатора накапливать электрический заряд является его основной характеристикой — ёмкостью. Величина ёмкости конденсатора определяется из выражения:
Где: e — относительная диэлектрическая проницаемость диэлектрика (вещества, которое заполняет пространство между пластинами конденсатора eo – диэлектрическая постоянная ( численно равна 8,854*10-12 Ф/м);
S – величина площади пластины м2;
d – расстояние между пластинами м.
Ещё одной важной характеристикой конденсатора является его номинальное напряжение. Это величина напряжения, при котором он может работать в заданных условиях в течении всего срока службы не меняя своих параметров. Если приложить номинальное напряжение к обкладкам конденсатора – осуществится зарядка конденсатора. Энергия заряженного конденсатора сосредоточена в его электрическом поле и определяется из выражения:
Где: U – величина напряжения, до которой заряжен конденсатор.
При разряде, энергия электрического поля конденсатора расходуется на работу связанную с перемещением зарядов – на создание электрического тока. В идеальном конденсаторе осуществляется циркуляция энергии: электрическая энергия накапливается в электрическом поле конденсатора на протяжении четверти периода, а в течении следующей четверти периода вновь возвращается в сеть.
По теореме Гаусса поток вектора D через цилиндр ничтожно малой высоты равен нулю (нет свободных зарядов) DnAS-Dn.AS = 0,
Таким образом, при переходе через границу раздела двух диэлектрических сред нормальная составляющая вектора D (Д.,) изменяются непрерывно (не претерпевают скачка), и тангенциальная составляющая вектора D (Dx) претерпевают скачок.
Дата добавления: 2015-04-21 ; просмотров: 84 ; Нарушение авторских прав
📸 Видео
Урок 218. Напряженность электрического поляСкачать

Билет №02 "Теорема Гаусса"Скачать

Урок 231. Свойства электрического потенциалаСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Связь напряжённости и потенциала (Задача 17)Скачать

физика 10-11 база. лекция 17. Электростатика. Потенциал. Связь напряженности и потенциала.Скачать

Физика. 10 класс. Эквипотенциальные поверхностиСкачать

Потенциал электрического поля. 10 класс.Скачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

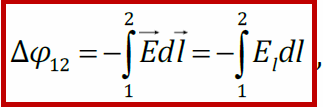
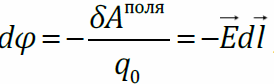

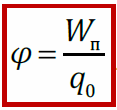
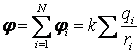
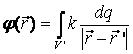
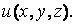
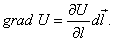
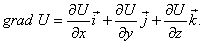
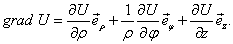
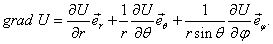
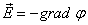



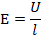




 — электрическая постоянная; произведение
— электрическая постоянная; произведение  называется в системе СИ абсолютной диэлектрической восприимчивостью.
называется в системе СИ абсолютной диэлектрической восприимчивостью.
 .
. через произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S:
через произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S: .
. (электрическое смещение). Теорема Гаусса для вектора
(электрическое смещение). Теорема Гаусса для вектора 
