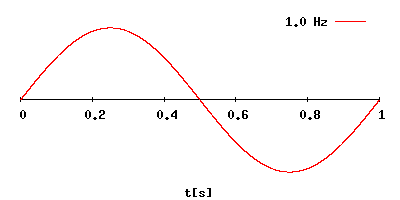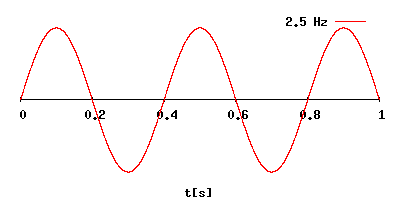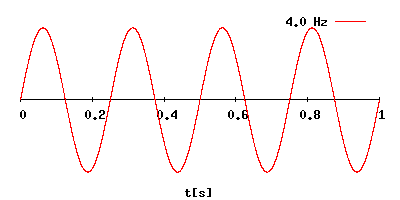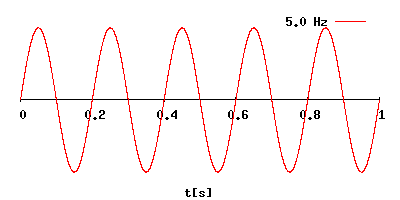
Онлайн калькуляторы: перевод частоты колебаний в период и, наоборот –
перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом:
F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц)
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой простых онлайн калькуляторов.
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ
А теперь всё то же самое, но наоборот:
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ПЕРИОДУ КОЛЕБАНИЙ
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
- Период и частота колебаний
- Колебательные процессы
- Период гармонических колебаний
- Частота гармонических колебаний
- Связь периода и частоты колебаний
- Что мы узнали?
- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
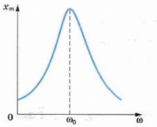
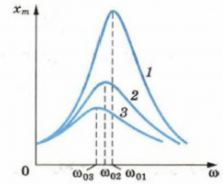
- Резонанс
- 💡 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Период и частота колебаний

Средняя оценка: 4.7
Всего получено оценок: 249.
Средняя оценка: 4.7
Всего получено оценок: 249.
Колебательные процессы – одни из наиболее широко распространенных процессов в природе. Важными характеристиками в этих процессах является период и частота колебаний. Рассмотрим эти параметры более подробно.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Колебательные процессы
Колебательным процессом называется периодическое изменение одного или нескольких параметров системы около некоторого значения. Например, колебательным процессом является флаг, развевающийся на ветру. Полотнище флага совершает хаотичные движения вокруг некоторого среднего положения, задаваемого ветром. Другим примером колебательного процесса является движение нитяного маятника – если груз, подвешенный на нити, отклонить от положения равновесия и отпустить, то он начинает колебаться вокруг положения равновесия.
В первом приведенном примере колебания являются хаотичными. Во втором примере – колебания подчиняются простому закону круговых функций (синусоиды), и называются гармоническими. В высшей математике доказывается, что любые сложные колебания могут быть описаны суммой гармонических колебаний. Поэтому в первую очередь изучаются именно они.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Период гармонических колебаний
Особенностью гармонических колебаний является их большая схожесть. Каждое колебание маятника почти полностью повторяет предыдущее и последующее.
В первую очередь это относится к «скорости качания». Если измерить время, за которое совершаются колебания маятника, можно убедиться, что оно для разных колебаний остается одинаковым. Взяв много маятников разных длин, можно получить различные колебания, однако, для каждого маятника время, за которое совершается любое колебание, будет постоянным.
Это время – важнейшая характеристика колебательного процесса. Оно называется периодом колебаний, обозначается латинской буквой $T$ и измеряется в секундах. Чем быстрее происходят колебания (чем короче нить маятника), тем меньше времени длится каждое колебание, и тем меньше период колебаний.
Видео:Урок 338. Сложение колебаний близких частот. БиенияСкачать

Частота гармонических колебаний
При работе с колебательными процессами нередки случаи, когда для характеристики «скорости» удобнее рассматривать не период одного колебания, а количество колебаний за единицу времени. Такая величина называется частотой колебаний, и обозначается греческой буквой $nu$ («ню»). Она равна отношению числа колебаний ко времени, за которое они происходят:
- N – число колебаний;
- t – время, за которое колебания произошли (сек).
Поскольку единицей времени в системе СИ является секунда, то единицей частоты является «колебание в секунду», или Герц (Гц).

Видео:Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

Связь периода и частоты колебаний
Из формулы частоты колебаний можно получить зависимость периода колебаний от частоты. Если колебания происходят с периодом $T$, то $N$ колебаний произойдут за время $TN$. Подставив это время в формулу, получим:
Таким образом, частота и период колебаний взаимнообратны. Зная частоту – легко найти период, а зная период – легко найти частоту.
Из математики известно, что на нуль делить нельзя. То есть, в формулу связи периода и частоты колебаний нельзя подставлять нулевой период или частоту – в обоих случаях такие колебания невозможны.
Видео:Физика Циклическая частотаСкачать

Что мы узнали?
Важнейшей характеристикой колебательных процессов является период колебаний, равный времени одного колебания. Зачастую удобно использовать величину, обратную периоду, которая называется частота колебаний.
Видео:Выполнялка 53.Гармонические колебания.Скачать

Гармонические колебания
теория по физике 🧲 колебания и волны
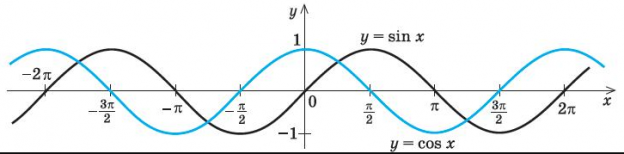
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
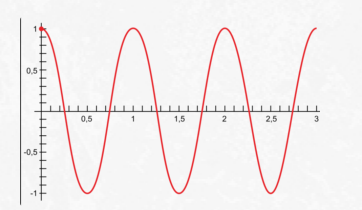
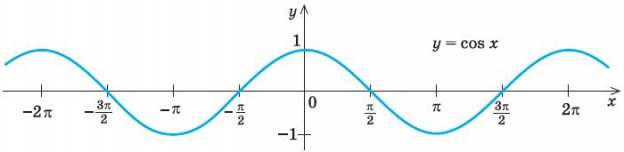
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:Урок 327. Гармонические колебанияСкачать

Уравнение движения гармонических колебаний
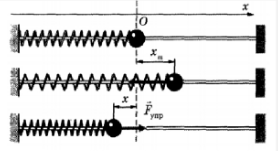
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:Амплитуда, период, частота и длина волны периодических волнСкачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
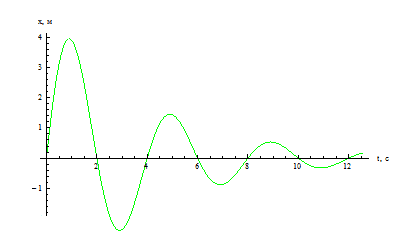
Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 |
| Фаза, ϕ (рад) | 0 |