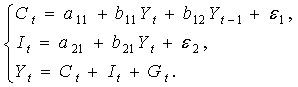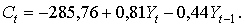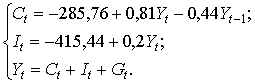Уравнение сверхидентифицируемо если выполняется счетное правило

Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Введем следующие обозначения:

М – число предопределенных переменных в модели;

m— число предопределенных переменных в данном уравнении;

— число эндогенных переменных в модели;

— число эндогенных переменных в данном уравнении;

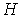
Обозначим число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через , .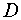

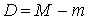
Тогда условие идентифицируемости каждого уравнения модели может быть записано в виде следующего счетного правила:

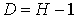	уравнение идентифицируемо
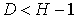	уравнение неидентифицируемо
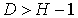	уравнение сверхидентифицируемо

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации.

Достаточное условие идентификации

Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но не достаточное условие идентификации.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны 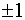. В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию структурных уравнений системы тождества участвуют..

Изучается модель (одна из версий модели Кейнса):

(7.8)

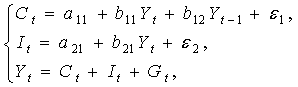
где – потребление в период ; – ВВП в период ; — ВВП в период ( ); – валовые инвестиции в период ; – государственные расходы в период .

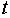
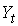
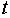
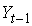
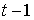
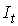
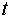
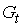
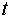
Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение –тождество ВВП. Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.

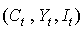
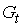
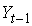
Модель включает три эндогенные переменные и две предопределенные переменные (одна экзогенная переменная – и одна лаговая переменная – ).

Проверим необходимое условие идентификации для каждого из уравнений модели.

N	Уравнение		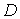счетное правило
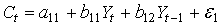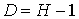		идентифицируемо
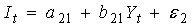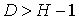		сверхидентифицируемо
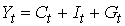	тождество, не подлежит проверке

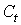
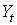
Например, первое уравнение содержит две эндогенные переменные и и одну предопределенную переменную .

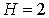
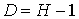
Таким образом, ; D=2-1=1. Условие условие выполняется, т. е. уравнение идентифицируемо.

Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

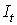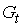I уравнение	-1	b11	b12	0	0
II уравнение	0	b21	0	-1	0
Тождество	1	0	0	1	1

В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.

Первое уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: 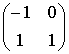. Ее определитель не равен нулю, поэтому ранг матрицы равен 2, т. е равняется числу эндогенных переменных без одного. Достаточное условие идентификации выполняется.

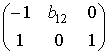
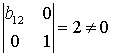
Второе уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: . Ранг данной матрицы равен 2, так как существут определитель второго порядка не равный нулю: . Следовательно, достаточное условие идентификации для данного уравнения также выполняется Но в соответствии с необходимым условием считаем это уравнение сверхидентифицируемым.

Таким образом, эта система уравнений является сверхидентифицируемой.

7.5. Методы оценки параметров структурной формы модели

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

1) косвенный метод наименьших квадратов;

2) двухшаговый метод наименьших квадратов;

3) трехшаговый метод наименьших квадратов;

4) метод максимального правдоподобия с полной информацией;

5) метод максимального правдоподобия при ограниченной информации.

Рассмотрим сущность некоторых из этих методов.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов:

1. Для структурной модели строится приведенная форма модели.

2. Для каждого уравнения приведенной формы традиционным МНК оцениваются приведенные коэффициенты .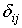

3. На основе коэффициентов приведенной формы находятся путем алгебраических преобразований параметры структурной модели.

Двухшаговый метод наименьших квадратов (ДМНК)

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод (ДМНК).

Основная идея ДМНК состоит в следующем:

· на основе приведенной формы модели получить для сверхидентифицируемого уравнения расчетные значения эндогенных переменных, содержащихся в правой части этого уравнения;

· подставляя найденные расчетные значения эндогенных переменных вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.

Метод получил название двухшагового МНК, ибо дважды используется МНК:

· на первом шаге при определении параметров приведенной формы модели и нахождении на их основе оценок расчетных значений эндогенных переменных ; ;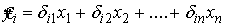

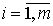
· на втором шаге применительно к структурному сверхидентифицируемому уравнению, когда вместо фактических значений эндогенных переменных рассматриваются их расчетные значения, найденные на предыдущем шаге.

Сверхидентифицируемая структурная модель может быть двух типов:

· все уравнения системы сверхидентифицируемы;

· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним можно найти на основе косвенного МНК. Двухшаговый метод, примененный к точно идентифицированным уравнениям дает такой же результат, что и косвенный МНК.

Продолжение примера 15.

Продолжим рассмотрение примера 15.

Система является сверхидентифицируемой: первое уравнение идентифицируемо, а второе уравнение сверхидентифицируемо. Поэтому для определения коэффициентов первого уравнения можно применить косвенный МНК, а для второго уравнении двухшаговый МНК.

Построим приведенную форму модели:

(7.9)

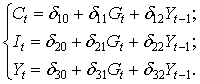
Исходные данные задачи (в млрд. руб.)

годы		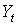		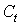		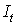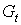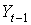Предсказанное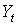
4823.23	2281.18	670.44	2629.62	4182,05
7305.65	3009.42	1165.23	1014.2	4823.23	6731,57
8943.58	3972.81	1504.71	1193.5	7305.65	9496,45
10830.54	5001.77	1762.41	1947.3	8943.58	11692,48
13243.24	6147.26	2186.37	2345.6	10830.54	13947,4
17048.12	7670.68	2865.01	2659.4	13243.24	16716,24
21625.37	9613.84	3611.11	3472.1	17048.12	21268,68
26903.49	11927.59	4730.02	4284.8	21625.37	26648,73
33258.14	14831.38	6716.22	26903.49	33297,77

Найдем параметры модели (7.9), применяя МНК к каждому уравнению,

используем « Пакет анализа» EXCEL):

(7.10)

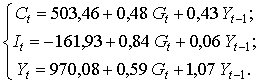
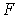
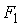
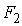
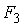
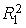
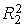
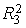
Каждое уравнение статистически значимо ( – статистики: =1302,55;

=281,956; =847,65). Коэффициенты детерминации свидетельствуют о хорошей связи между эндогенными и предопределенными переменными: =0,9977; =0,989; =0,996.

На основе уравнений модели (7.10) найдем структурные коэффициенты первого уравнения.

Выразим из третьего уравнения (7.10) переменную 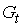и подставим в первое уравнение. Получим первое структурное уравнение:

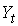
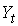
Так как второе уравнение сверхидентифицировано, то применим двухшаговый МНК. Найдем на основе третьего уравнения (7.10) расчетные значения переменной ( столбец «предсказанное » табл.23) и используем их для нахождения параметров второго структурного уравнения.

Получим: 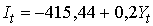4; .

В результате получим следующую систему структурных уравнений:

Трехшаговый метод наименьших квадратов (ТМНК)

Трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и случайные остатки каждого уравнения. Затем строится ковариационная матрица остатков и проводится ее оценка. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. ТМНК является достаточно эффективным, но требует существенно больших вычислительных затрат. Более подробное описание можно найти в работе[1][1]

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Системы эконометрических уравнений (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Объектом статистического изучения в социальных науках являются сложные системы. Построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования. Изменение одной переменной, как правило, не может происходить без изменения других. Поэтому важное место занимает проблема описания структуры связей между переменными системой так называемых одновременных уравнений. Так, если изучается модель спроса как отношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.

Системы уравнений здесь могут быть построены по – разному.

Возможна система независимых уравнений, когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x :

(1)

Набор факторов xj в каждом уравнении может варьироваться. Каждое уравнение может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. По существу, каждое уравнение этой системы является уравнением регрессии.

Наибольшее распространение в эконометрических исследованиях получила система одновременных (совместных, взаимозависимых) уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть:

(2)

В эконометрике эта система уравнений называется также структурной формой модели. Для нахождения параметров каждого уравнения традиционный МНК неприменим, здесь используются специальные методы оценивания. В этом случае каждое из уравнений не может рассматриваться самостоятельно.

Структурная и приведенная формы модели.

Система одновременных уравнений (т. е. структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y

Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Они обозначаются через x .

Простейшая структурная форма модели имеет вид:

где y 1 , y 2 — эндогенные переменные, x 1 , x 2 — экзогенные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других — как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года yt может зависеть также и от уровня потребления в предыдущем году yt -1 .

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Коэффициенты при эндогенных и — при экзогенных переменных называются структурными коэффициентами модели. Все переменные в модели могут быть выражены в отклонениях и от среднего уровня, и тогда свободный член в каждом уравнении отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

(3)

коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Приведенная форма позволяет выразить значения эндогенных переменных через экзогенные, однако аналитически уступает структурной форме модели, т. к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

Видео:Решение систем уравнений методом подстановкиСкачать

Проблема идентификации

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (2) в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n ( n -1+ m ) параметров. Приведенная модель (3) в полном виде содержит nm параметров. Таким образом, в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Поэтому n ( n -1+ m ) параметров структурной модели не могут быть однозначно определены через nm параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели равны нулю. Тем самым уменьшится число структурных коэффициентов.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. число параметров структурной модели равно числу параметров приведенной формы модели.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель (2) в полном виде всегда неидентифицируема.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенных коэффициентов можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой, практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Обозначим Н – число эндогенных переменных в i — ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда условие идентифицируемости уравнения может быть записано в виде следующего счетного правила:

D+1 = Н – уравнение идентифицируемо;

D+1 Н – уравнение неидентифицируемо;

D+1 > Н – уравнение сверхидентифицируемо.

Это счетное правило отражает необходимое, но не достаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

где M – доля импорта в ВВП;

N – общее число прошений об освобождении от таможенных пошлин;

S – число удовлетворенных прошений;

E – фиктивная переменная, означающая, является ли курс доллара искусственно завышенным или нет;

Y – реальный ВВП;

X – реальный объём чистого экспорта;

t – текущий период;

t -1 – предыдущий период.

Проверим данную модель на идентификацию и определим, каким методом могут быть рассчитаны её коэффициенты (в случае, если модель сверх – или точно идентифицируема).

Сначала рассмотрим общие характеристики структурной формы. Здесь три эндогенные переменные – Mt , Nt и St , они стоят в левых частях уравнений. Кроме того, в правых частях находятся четыре предопределенные переменные – одна лаговая ( Mt -1 ) и три экзогенные – Et -1 , Yt и Xt . Теперь проверим каждое уравнение.

Уравнение I . В этом уравнении присутствуют три эндогенные переменные ( Mt , Nt и St ), но отсутствуют две предопределенные переменные — Yt и Xt . Поэтому Н=3 , D =2 , и необходимое условие идентификации выполняется, поскольку D +1= H . Это означает, что первое уравнение точно идентифицируемо.

Уравнение II . В этом уравнении присутствуют три эндогенные переменные ( Mt , Nt и St ), но отсутствуют три экзогенные — Е t — 1 , Mt -1 и Xt . Поэтому Н=3 , D =3 , D +1> H и второе уравнение по необходимому условию является сверхидентифицируемым.

Уравнение III . В этом уравнении, как и в других уравнениях, присутствуют все три эндогенные переменные, но отсутствуют три экзогенные — Е t — 1 , Mt -1 и Yt . Поэтому Н=3 , D =3 , D +1> H , и третье уравнение системы является сверхидентифицируемым.

Проверим каждое уравнение на выполнение достаточного условия идентификации. Для этого сначала запишем расширенную матрицу системы в виде следующей таблицы:

Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

14. Проблема идентификации

При переходе от приведенной формы модели к структурной сталкиваются с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (3.3) в полном виде содержит параметров, а приведенная форма модели в полном виде содержит параметров. Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно параметров структурной модели не могут быть однозначно определены из параметров приведенной формы модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель Идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель Неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель Сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в I-м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, – через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

Рассмотрим Пример. Изучается модель вида

Где – расходы на потребление в период T, – совокупный доход в период T, – инвестиции в период T, – процентная ставка в период T, – денежная масса в период T, – государственные расходы в период T, – расходы на потребление в период , инвестиции в период . Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.

Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.

Модель включает четыре эндогенные переменные и четыре предопределенные переменные (две экзогенные переменные – и и две лаговые переменные – и ).

Проверим необходимое условие идентификации для каждого из уравнений модели.

Первое уравнение: . Это уравнение содержит две эндогенные переменные и и одну предопределенную переменную . Таким образом, , а , т. е. выполняется условие . Уравнение сверхидентифицируемо.

Второе уравнение: . Оно включает две эндогенные переменные и и одну экзогенную переменную . Выполняется условие . Уравнение сверхидентифицируемо.

Третье уравнение: . Оно включает две эндогенные переменные и и одну экзогенную переменную . Выполняется условие . Уравнение сверхидентифицируемо.

Четвертое уравнение: . Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.

Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

📺 Видео

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Уравнение. 5 класс.Скачать

Уравнение движенияСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Равносильность уравнений. Уравнение – следствие | Алгебра 11 класс #24 | ИнфоурокСкачать

Как решить симметрическое уравнение | Сведение к квадратному | Замена переменнойСкачать

Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

Решить интегральное уравнение (ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ) Свёртка функций, Умножение изображенийСкачать

Характеристическое уравнение в ДУСкачать

Показательно степенное уравнениеСкачать

Линейные диофантовы уравненияСкачать

Математика без Ху!ни. Как вычислить определитель.Скачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Разностное функциональное уравнение решено двумя способами.Скачать

Числовые Промежутки — Алгебра 8 класс / Подготовка к ЕГЭ по МатематикеСкачать