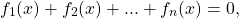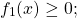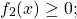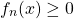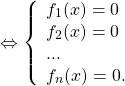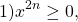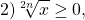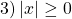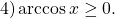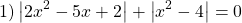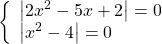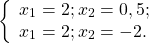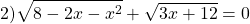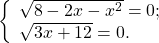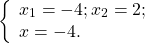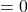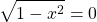Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Применение общего свойства модуля, квадратного корня и квадрата некоторого выражения.
Готовясь к итоговой аттестации в 9 классе, ребята часто сталкиваются с нестандартными заданиями, которые не встретишь в учебнике, но решаются они просто, если обратить внимание на одну особенность модуля, квадратного корня и квадрата некоторого выражения, в частности на то, что все эти выражения при любом значении переменной больше или равны нулю.
Рассмотрим некоторые задания из сборников для подготовки к ОГЭ
Решить уравнение: ( х² -1)² +( х²-6х-7)² =0
Решение: Т.к. квадрат любого выражения больше либо равен нулю, то сумма двух квадратов будет равна нулю только в том случае, когда оба эти выражения равны нулю одновременно, т.е.
Заметим, что при х= — 1 эти выражения равны нулю одновременно, а значит и их сумма равна нулю.
Найти наименьшее значение выражения: | 2х + у + 1|+| — 3х – 4у + 6| и указать при каких значениях х и у это достигается.
Т.к. модуль любого выражения больше либо равен нулю, то сумма модулей будет наименьшей при условии, что оба модуля будут равны нулю и достигаться это будет если
Решая эту систему имеем: х= — 2; у=3
Ответ Наименьшее значение выражения | 2х + у + 1|+| — 3х – 4у + 6| равно нулю при х= — 2 ; у=3.
Решить уравнение: 
+ 
= 0
Конечно данное уравнение можно решать как иррациональное, но 9- классники не умеют этого делать, поэтому воспользуемся тем же свойством, что и в первых двух примерах.
Т.к каждый корень квадратный больше либо равен нулю, то сумма корней равна нулю при условии, что каждый равен нулю одновременно, т.е.
х ² — 9=0 и (х – 3)(х – 2)=0
Курс повышения квалификации
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- В уравнении сумма равна 0
- Квадратное уравнение. Дискриминант. Теорема Виета.
- теория по математике 📈 уравнения
- Дискриминант
- Теорема Виета
- 📺 Видео
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 315 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:ОГЭ 2021 № 20 Сумма квадратов равна нулю. Равносильный переход. a^2+b^2=0Скачать
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 591 916 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 09.02.2016
- 619
- 2
- 09.02.2016
- 1159
- 5
- 09.02.2016
- 427
- 0
- 09.02.2016
- 433
- 0
- 09.02.2016
- 537
- 0
- 09.02.2016
- 1888
- 1
- 09.02.2016
- 702
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.02.2016 831
- DOCX 23 кбайт
- 3 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Шукова Татьяна Леонидовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 1 месяц
- Подписчики: 4
- Всего просмотров: 4921
- Всего материалов: 11
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:ОГЭ 2021 | Сумма квадратов равна нулю | Как нужно рассуждать ?Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
РДШ организовало сбор гуманитарной помощи для детей из ДНР
Время чтения: 1 минута
В Швеции запретят использовать мобильные телефоны на уроках
Время чтения: 1 минута
Минпросвещения упростит процедуру подачи документов в детский сад
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:ОГЭ 2021 Сумма квадратов двух выражений равна нулю. Решается очень легко a^2+b^2=0Скачать
В уравнении сумма равна 0
Мы уже рассматривали уравнения, равные нулю (типа «произведение равно нулю»). К виду «произведение равно нулю» сводятся многие уравнения из разных разделов алгебры.
Если в уравнении сумма равна нулю, в некоторых случаях его можно решить, применяя следующее свойство функций:
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда каждая из функций равна нулю.
Таким образом, уравнение
равносильно системе уравнений
где 2n — чётное натуральное число
Примеры уравнений, решение которых основано на этом свойстве функций.
Сумма модулей равна нулю, если каждое из слагаемых равно нулю. Поэтому данное уравнение равносильно системе
Найдём корни каждого уравнения:
Оба модуля обращаются в нуль при x=2.
Сумма корней чётной степени равна нулю, если каждое из слагаемых рано нулю. Следовательно, это уравнение равносильно системе
Решаем каждое уравнение:
Оба слагаемых обращаются в нуль при x= -4.
Для нахождения корней достаточно решить только одно из уравнений и проверить, удовлетворяют ли полученные корни остальным уравнениям системы.
Сумма неотрицательных функций равна нулю, если каждая каждая из функций равна нулю:
Корень третьего уравнения — x=9 — удовлетворяет также 1-му и 2-му уравнениям системы.
Правая часть уравнений — сумма неотрицательных функций. Соответственно, уравнение равносильно системе
Корни второго уравнения
x=1 и x= -1. Оба корня удовлетворяют и первому уравнению.
Как в другие уравнения из курса алгебры, решаемые с применением свойств функций, уравнения, в которых сумма неотрицательных функций равна нулю, при первом рассмотрении могут производить впечатление сложных. На самом деле, решить их достаточно просто, если помнить соответствующий теоретический материал.
Видео:Сумма квадратов натуральных чисел через комбинаторику. Пример от wild mathing!Скачать
Квадратное уравнение. Дискриминант. Теорема Виета.
теория по математике 📈 уравнения
Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.
Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.
Видео:Разность квадратов двух выражений. 7 класс.Скачать
Дискриминант
Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).
Нахождение корней квадратного уравнения
Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:
D=b 2 –4ac
- Если D>0, то уравнение имеет два различных
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:
Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.
D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Видео:Урок 2. Сумма двух квадратов равна нулю.Скачать
Теорема Виета
Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.
Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.
Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.
Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:
Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.
Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:
Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
📺 Видео
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
ЗАДАЧА О СУММЕ КВАДРАТОВСкачать
При каких значениях а сумма квадратов корней уравнения x² + ax + a - 2 = 0 минимальна?Скачать
#67. Сумма квадратов корней в уравнении с параметром!Скачать
Быстрый способ решения квадратного уравненияСкачать
Сумма квадратов равна нулю Д429Скачать
Решите уравнение ➜ Определитель третьего порядка равен нулюСкачать
№953. Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналейСкачать
Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать
Задание №20 Сумма квадратов двух выраженийСкачать
6. Квадратное уравнение. Дискриминант равен нулю.Скачать
Найти сумму корней квадратного уравнения, если дискриминант равен нулюСкачать
ОГЭ 2021 Сумма модуля и квадрата. EASY РЕШЕНИЕСкачать
Площадь под степенной функцией на отрезке. Древние способы. Сумма квадратов и сумма кубовСкачать
