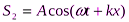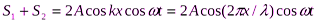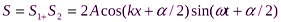Уравнение стоячей волны 2acoskxcoswt амплитуда равна (6 видео)

Уравнение стоячей волны 2acoskxcoswt амплитуда равна

§4 Интерференция волн.

Принцип суперпозиции. Понятие о когерентности волн

Если в среде распространяется несколько волн одновременно, то колебания частиц среды равны геометрической сумме колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются, не возмущая друг друга – принцип суперпозиции (наложения) волн.

Две волны называются когерентными, если разность их фаз не зависит от времени

—
условие когерентности.

Источники когерентных волн называются когерентными источниками.

т.к. для когерентных источников разность начальных фаз , то амплитуда А_резв различных точках зависит от величины , называемой разностью хода. Если

то наблюдается максимум.

При наложении волн от когерентных источников наблюдаются минимумы и максимумы, результирующей амплитуды, т.е. взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих, волн — суть явления интерференции.

§5 Стоячие волны

Частным случаем интерференции являются стоячие волны — волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу волн с одинаковыми амплитудами н частотами.

Для вывода уравнения стоячей волны примем: 1) волны распространяются в среде без затухания; 2) А₁ = А₂ =А — имеют равные амплитуды; 3) ω₁ = ω₂= ω — равные частоты; 4)φ₁₀ = φ₂₀ = 0.

Уравнение бегущей волны, распространяющейся вдоль положительного направления оси х (т.е. уравнение падающей волны):

(1)

Уравнение бегущей волны, распространяющейся в отрицательном направлении оси х (т.е. уравнение отраженной волны):

(2)

Сложив (1) и (2) получим уравнение стоячей волны:

Особенностью стоячей волны является то, что амплитуда зависит от координаты х. При перемещении от одной точки к другой амплитуда меняется по закону:

— амплитуда стоячей волны.

Те точки среды, в которых амплитуда стоячей волны максимальна и равна 2А, называются пучностями. Координаты пучностей можно найти из условия, что

Расстояние между двумя соседними пучностями равно .

Точки, в которых амплитуда стоячей волны минимальна и равна 0 , называются узлами. Координата узлов можно найти из условия

Расстояние между двумя соседними узлами равно .

В отличие от бегущей волна, все точки которой колеблются с одинаковой амплитудой, но с разными фазами, зависящими от координаты х точки ( ), точки стоячей волны между двумя узлами колеблется с разными амплитудами, но с одинаковыми фазами( ). При переходе через узел множитель меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на π, т.е. точки лежащие по разные стороны от узла колеблются в противофазе.

Стоячая волна получается в результате интерференции падающей и отраженной волн. На характере отражения сказывается граница раздела двух сред, от которой происходит отражение. Если волна отражается от среды менее плотной (рис. а), то фаза волны на границе раздела не меняется и на границе раздела двух сред будет пучность. Если волна отражается от более плотной среды, то её фаза изменяется на противоположную, т.е. отражение от более плотной среды происходит с потерей половины длины волны (λ/2). Бегущая волна переносит энергию колебательного движения в направлении распространения волны. Стоячая волна энергию не переносит, т.к. падаюшая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узлами остается постоянной. Лишь в пределах расстояний равных λ/2 происходит превращение кинетической энергии в потенциальную.

Содержание

Узлы стоячей волны
Стоячие волны
Стоячие волны
Наложение двух волн, бегущих в противоположные стороны
Собственные колебания стержней
Стержень, открытый с обоих концов
Стержень, закрепленный в одном конце
Собственные колебания двумерных и трехмерных систем
Вынужденные колебания стержней и пластинок
Колебания пьезоэлектриков
📸 Видео

Видео:Стоячие волны. 11 класс.Скачать

Узлы стоячей волны

Стоячие волны

Волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Уравнение стоячей волны

(учли, что k = 2π/λ)—уравнение стоячей волны.

Пучности стоячей волны

Точки, в которых амплитуда максимальна (A_ст = 2Аcos(2πx/λ)) . Это точки среды, для которых

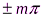
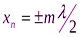
2πx/λ= (m=0,1,2,….)

(m = 0,1, 2. ).

Узлы стоячей волны

Точки, в которых амплитуда колебаний равна нулю (A_ст = 0). Это точки среды, для которых

(m = 0,1, 2. ).

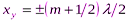
Расстояния пучность—пучность и узел—узел равны λ/2, а расстояние пучность—узел равно λ/4.

Образование стоячих волн наблюдают при

интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит, и у границы колебания складываются с одинаковыми фазами — получается пучность.

Уравнение стоячей волны и его анализ

Частным случаем интерференции волн, являются стоячие волны.

Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.

Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.

При наложении двух когерентных бегущих плоских волн вида

и где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением

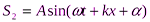
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.

Точки ,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.

Положение узлов и пучностей находится из условий

k*x+α/2=m*n (пучности) ,где m=0,1,2…

Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.

В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.

Видео:Урок 375. Стоячие волныСкачать

Стоячие волны

Содержание:

Стоячая волна — это волна, которая образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Видео:Галилео. Эксперимент. Стоячая волнаСкачать

Стоячие волны

Стоячая волна — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует.

Наложение двух волн, бегущих в противоположные стороны

Положим, что две плоские волны, вполне одинаковые по своим характеристикам, идут навстречу друг другу. Нас интересует возникающее колебательное движение среды, в которой распространяются волны.

Как упоминалось выше, различие в направлении распределения учитывается различием в знаках координаты в уравнении волны. Следовательно, результирующая картина смещения должна передаваться выражением

Результат вычисления весьма интересен. Сумма двух бегущих волн не дала волнового движения. Полученная формула указывает на наличие колебаний с амплитудой разной в разных местах пространства. Своеобразное колебательное состояние среды, возникающее при движении в противоположные стороны двух одинаковых бегущих волн, носит название стоячей волны. Еще раз подчеркнем, что стоячая волна не есть волна. Бегущая волна переносит энергию, в стоячей волне никакой передачи энергии от точки к точке нет; бегущая волна может двигаться вправо или влево, у стоячей волны нет направления распространения. Это название характеризует колебательное состояние среды.

В чем же особенности этого колебательного состояния? Прежде всего, мы видим, что колеблются не все точки среды. В местах пространства, удовлетворяющих условиях амплитуда колебания равна нулю. Соответствующие места носят название узлов стоячей волны. Расстояние между двумя соседними узлами вдоль оси х, по которой были пущены бегущие волны, равно половине длины волны. Между двумя узлами лежат точки, которые колеблются с наибольшей амплитудой, равной 2А. Эти точки называются пучностями стоячей волны.

На рис. 64 представлено колебательное состояние, соответствующее стоячей волне для нескольких последующих моментов времени. Мы видим, что название вполне оправдано. В каждое мгновение видна волна. При этом волна стоит на месте. Если делать мгновенные фотографии одну за другой, то точки пересечения волной оси абсцисс — узлы — будут оставаться на одном и том же месте. Волна стоит. Изменения в мгновенных снимках будут состоять в изменении величины смещений. Наступит такой момент, когда все точки среды будут неподвижными. По прохождении этого мгновения точки, отклонявшиеся кверху, будут идти вниз, и наоборот. Разумеется, нарисованная картина не имеет ничего общего с бегущей волной, где два «мгновенных снимка» выглядят так, как на ранее приведенном рис. 57. Там волна движется, максимумы и минимумы волны в каждое следующее мгновение переходят в новые места.

Мы сказали, что в стоячей волне передачи энергии нет. Как описать тогда в терминах энергии процессы, происходящие в этом своеобразном колебательном движении? Очевидно, что энергия стоячей волны (какой-либо области, в которой она существует) есть величина постоянная.

В тот момент, когда все точки проходят положение равновесия, вся энергия точек, захваченных

колебанием, является кинетической. Напротив, в положении максимального отклонения точек от положения равновесия энергия всех точек тела является потенциальной.

Стоячая волна — важнейший колебательный процесс: разного вида стоячие волны ‘возникают в телах ограниченных размеров, по которым распространяются упругие волны. Дело заключается в том, что упругие волны отражаются от границы тела со средой и отправляются в среду обратно. В ограниченном теле возникает сложное колебательное состояние, являющееся результатом наложения на исходную волну всех других волн, которые отразились от стенок и вернулись в среду. Ряд типичных случаев будет сейчас рассмотрен.

Собственные колебания стержней

Ударом или иным способом в каждом твердом стержне можно возбудить продольную упругую волну, распространяющуюся вдоль его длины. От противоположного конца стержня эта волна отразится, и, таким образом, весь стержень придет в колебательное состояние, изображаемое стоячей волной. Это колебательное состояние будет свободным, так как оно возникнет благодаря кратковременному импульсу и будет далее продолжаться без действия внешних сил. Ряд сведений о характере этих свободных колебаний мы получим, если положим известной длину стержня и укажем способ его закрепления. Длина стержня и способ его закрепления дают нам так называемые граничные условия. Они сводятся к следующему: в закрепленном месте стержня существует узел стоячей волны, на открытом конце стержня образуется пучность стоячей волны.

Рассмотрим несколько способов возбуждения продольных свободных колебаний в стержне с длиной

Стержень, закрепленный в обоих концах. В этом случае на концах стержня должны образоваться узлы волны смещений. Так как расстояние между узлами равно половине длины волны, то возможные длины волн связаны с длиной стержня условием т. е.— любое целое число.

Используя для скорости упругой волны выражение и вспоминая связь частоты с длиной волны, получим выражение для собственных частот свободных продольных колебаний стержня

Прежде всего необходимо подчеркнуть принципиально новый для нас результат. Сплошное тело имеет не одну, а множество собственных (характеристических) частот колебания. Соответственное этим разнообразны возможные свободные колебания стержня. Стержень может также совершать негармонические колебания с любым спектром *), составленным из частот

Частота V! является основной частотой колебания стержня. Ей соответствует колебательное движение с условием Это значит, что при основном колебании центр стержня лежит в пучности стоячей волны, а узлов между концами стержня нет. Колебанию во втором обертоне (вторая гармоника) соответствует условие Теперь в центре стержня имеется узел. Если возбуждена третья гармоника, то между концами стержня будут лежать два узла, и т. д.

Пример. Для железного стержня длиной 7 м основная частота

Стержень, открытый с обоих концов

Если стержень подвесить на нитях, а затем возбудить в нем колебания, то возникшая стоячая волна должна удовлетворять условию: на обоих концах стержня существует пучность. Так же как и в предыдущем случае, между длиной стержня и длинами волн возникает связь: Следовательно, формула собственных частот будет той же самой.

Отличие от предыдущего случая заключается в распределении узлов и пучностей. В основном колебании центр стержня покоится (узел). Если возбуждена вторая гармоника, то в центре стержня будет пучность, далее через четверть длины волны — узлы и на краях — пучности.

Стержень, закрепленный в одном конце

В этом случае на одном конце должен быть узел, а на другом — пучность. При колебании с основной частотой стержень имеет форму, соответствующую одной четверти периода синусоиды. Так как расстояние между узлом и пучностью равно то связь между длинами волн и длиной стержня дается условием

Собственные частоты колебаний такого стержня выразятся формулой

Если в первых двух случаях частоты относились друг к другу, как целые числа, то теперь отношение частот дается отношением нечетных чисел.

Стержень, закрепленный в середине, будет в этом месте иметь узел, а на концах — пучности. Задача ничем не отличается от рассмотренной.

Граничные условия, которые использовались при рассмотрении колебательного состояния стержней, являются предельным случаем граничных условий отражения волн, изложенных на стр. 111., Как было выяснено ранее, при отражении от границы, отделяющей среду от среды с большим сопротивлением, происходит отражение волны смещения с потерей полволны. Если стержень закреплен, то волна вовсе не проникает во вторую среду. В этом случае можно говорить о бесконечно большом сопротивлении второй среды. Коэффициент отражения становится равным единице и отражение происходит с потерей полволны. Нетрудно видеть, что это соответствует наличию узла на границе двух сред. Отражение волны от незакрепленного конца стержня соответствует отражению от среды с нулевым сопротивлением. Равенство коэффициента отражения единице-и отсутствие потери полволны приводят к необходимости существования пучности на такой границе.

Продольные собственные колебания могут быть также возбуждены в столбах жидкости и столбах газа. Поперечные собственные колебания легко возбудить в зажатой и натянутой струне. Распределение узлов н пучностей будет, разумеется, таким же, как и для закрепленного с обоих концов стержня. Набор частот выразится формулой, аналогичной приведенной для стержня, с тем лишь различием, что в выражении скорости поперечной волны в струне надо заменить на натяжение струны, т. е. на частное от деления силы, натягивающей струну, на поперечное сечение струны.

Собственные колебания двумерных и трехмерных систем

В стержнях, струнах, воздушных столбах поверхности равной фазы представляют собой параллельные плоскости. Колебательное состояние можно представить себе как результат наложения плоских волн, распространяющихся вдоль одной линии. Однако возможны и более сложные случаи, а именно такие, когда колебательным движением захвачена двумерная область (пластинка, мембрана) или тело, все три размера которого имеют одинаковый порядок величины.

С двумерными задачами мы сталкиваемся, рассматривая колебания упругих и жестких диафрагм. Колебания разного типа возникнут, если в одном случае закрепить пластинку по краям, а в другом — укрепить ее в одной точке или даже не закреплять вовсе. Кроме колебаний жестких пластинок наблюдают колебания натянутых нежестких пленок — резиновых, мыльных и пр.

Общие закономерности свободных колебаний в этом случае в принципе не отличаются от рассмотренных. Ввиду двумерности задачи узлы и пучности должны характеризоваться теперь кривыми линиями. Например, круглая закрепленная по краям пластинка совершает основное колебание, имея единственную пучность в центре круга. Центральная точка колеблется с максимальной амплитудой, а далее амплитуда спадает к закрепленным краям (к узловой окружности) с сохранением круговой симметрии. Так выглядит простейшее колебание основной (самой низкой) частоты. Мембрана может быть возбуждена и в более высоких гармониках, тогда поверхность ее разбивается на участки узловыми линиями. Оказывается, что узловые линии у круглых пластинок могут иметь форму либо окружностей, либо диаметров, проходящих через центр.

Эффектным и простым опытом является демонстрация узловых линий способом Хладни (по имени ученого, предложившего этот способ). Пластинку посыпают песком, а затем ударом или смычком приводят в колебательное состояние. Песок скатывается с пучностей и собирается на узловых линиях. На рис. 65 показано несколько примеров фигур Хладни.

Естественно, наиболее сложным является колебательное состояние сплошного трехмерного тела. Отказываясь от рассмотрения явления в теле сложной формы, мы ограничим себя изучением собственных колебаний прямоугольного параллелепипеда. Если бы в таком теле существовали только стоячие волны, возникшие благодаря сложению волн, бегущих параллельно ребру параллелепипеда, то собственные частоты колебаний ограничивались бы значениями

а волновые числа (так называют величины, обратные длине волны) будут равны
где — любые целые числа,— длины ребер параллелепипеда.

Однако в теле могут распространяться волны, идущие под произвольным углом к границам. Стоячие волны образуются в том случае, если после ряда отражений луч придет в ту же точку, из которой он вышел. Волновое число такого луча должно вычисляться из по правилу сложения векторов. Таким образом,

Ясно, что частоты колебаний для простейших случаев распространения волн параллельно ребрам тела также получатся из этой формулы, если положить отличным от нуля лишь одно из трех целых чисел, входящих в формулу.

Спектр колебания трехмерного тела изображается в трехмерном пространстве (рис. 66), которое можно назвать пространством частот, или обратным пространством. Если величины откладывать соответственно по трем осям, то возникнет решетка, (обратная решетка), каждый узел которой представляет одну из собственных частот колебания тела за номерами Радиус-вектор обратного пространства, проведенный в узел решетки, равняется возможной частоте колебания. Если провести сферу радиусом то в нее попадут все точки, изображающие частоты, меньшие Объем такой сферы равен объем каждой ячейки обратной решетки

равен — объем тела. Следовательно, число собственных колебаний тела с частотами, меньшими (число узлов в октанте сферы), выражается формулой

Эта интересная закономерность показывает, что число собственных частот резко возрастает, если мы начнем увеличивать интервал частот, подлежащий рассмотрению. При больших частотах дискретный характер спектра начинает смазываться, частоты становятся весьма близкими друг к другу.

Вынужденные колебания стержней и пластинок

Если колебания стержня, пластинки или иного тела происходят не в вакууме, а в какой-либо среде *), жидкой или газообразной, то некоторая часть интенсивности, зависящая, как нам известно, от отношения волновых сопротивлений соприкасающихся сред, переходит из колеблющегося тела в среду. Можно выразить эту же мысль короче: колеблющееся тело излучает энергию. Благодаря излучению свободные колебания стержня, струны и пр. быстро затухают. Если нужно, чтобы такое тело являлось постоянным источником излучения, то колебания следует возбуждать посторонним источником. Так же как и в случае колебаний точки, подведение энергии может произойти как по схеме автоколебаний, так и созданием вынужденных колебаний.

В зависимости от способа и места подведения внешней энергии можно возбудить, вообще говоря, любую из частот или любую комбинацию собственных частот способного колебаться тела. Можно, например, следующим образом создать вынужденные колебания натянутой струны. Около стальной струны укрепляется электромагнит, питаемый синусоидальным током от звукового генератора. Колебания струны под действием периодически меняющейся внешней поперечной силы станут заметными лишь в случае резонанса. Подбирая разные натяжения струны и варьируя внешнюю частоту, можно продемонстрировать колебание струны на основной частоте, а также и на более высоких обертонах.

Огромное практическое значение имеет создание вынужденных колебаний (стоячих волн) в пьезоэлектрических пластинках и ферромагнитных стержнях. Эти колеблющиеся тела являются источниками ультразвуковые волн.

Ферромагнитные тела обладают свойством удлиняться или укорачиваться под действием магнитного поля. Теория этого явления сложна и мы скажем о ней и в дальнейшем лишь немногое. Пока что для нас достаточно знать, как изменяется длина ферромагнитного стержня в зависимости от напряженности поля. На этот вопрос отвечает рис. 67, из которого следует, что никель и отожженный кобальт укорачиваются в полях любой силы, литой кобальт в малых полях укорачивается, а в больших удлиняется и, наконец, железо удлиняется в малых полях и укорачивается в больших. Так или иначе, любой ферромагнитный стержень будет способен совершать вынужденные колебания при внесении в переменное магнитное поле. Для этой цели стержень помещают обычно в отверстие сердечника трансформатора, через который проходит переменный ток. Чтобы стоячая волна в стержне была достаточно сильной, необходимо работать в условиях резонанса: частота переменного поля должна совпадать с собственной частотой колебания стержня.

Так как стержень закрепляют в середине, то собственная частота колебанийпричем стержень может совершать колебания только на нечетных гармониках. Основная частота для никеля, если подставить значения физических констант, окажется равной

Например, стержень длиной 40 см будет колебаться с основной частотой 6 кГц.

Наиболее распространенным источником ультразвуковых колебаний является пьезокварц.

Колебания пьезоэлектриков

Как будет рассказано ниже (§ 262), все кристаллы, не обладающие в числе своих элементов симметрии центром симметрии, могут обладать пьезоэлектрическим эффектом. Это явление заключается в изменении размеров кристалла под действием электрического поля и, обратно, в возникновении электрического поля в кристалле под действием приложенных к кристаллу сил. При использовании пьезэ-электрика в качестве источника колебаний мы, естественно, интересуемся первым явлением, называемым также электрострикцией, или обратным пьезоэлектрическим эффектом. В качестве пьезоэлектриков употребляют кварц, сегнетову соль, титанат бария,дигидрофос-фат аммония и другие кристаллы. Вообще говоря, имеются сотни известных веществ, которые могли бы в принципе использоваться для той же цели. Однако наличие дополнительных требований (прочность, устойчивость к влаге и пр.), а также, разумеется, желание выбрать кристаллы, дающие наиболее сильный эффект, резко ограничивают практический список веществ.

Кристалл, помещенный в электрическое поле, меняет свои размеры в разных направлениях (по отношению к осям симметрии кристалла) по-разному. Поэтому, вырезая из кристалла стержни или пластинки, различно ориентированные по отношению к осям кристалла, и помещая их между обкладками конденсатора, мы будем получать деформации разного типа. Чаще всего вырезают пластинку кварца или другого пьезоэлектрика таким образом, чтобы под действием электрического поля в ней происходили продольные смещения. Тогда под действием переменного электрического поля в такой пластинке возникнут вынужденные стоячие продольные волны.

Если — толщина пластинки в направлении движения волны, то собственные частоты колебания представятся, как обычно, формулой Для кварца в этой простейшей ориентировке скорость увру-гих волн равна 5400 м/с. Следовательно, основная собственная частота колебания кварцевой пластинки найдется по формуле

(опыт дает несколько иное значение: 2880// кГц).

Амплитуды колебаний зависят от величины прикладываемого поля. Между величиной смещения и напряженностью электрического поля существует линейная зависимость. Прибегают к довольно сильным полям. Кварц — превосходный изолятор, поэтому при толщинах до сантиметра применяются электрические поля порядка 30 000 В/см.

Основным в получении сильного ультразвукового сигнала является резонансный эффект. Смещения под действием статического поля в тысячи раз меньше резонансных смещений, а ведь энергия колебания пропорциональна квадрату смещения.

Если повышать частоту генератора, можно последовательно возбудить пластинку на всех ее обертонах. Частоты наиболее распространенных промышленных ультразвуковых генераторов лежат в пределах от сотен до тысяч килогерц.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.