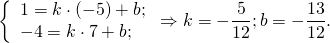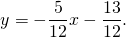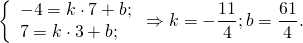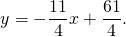1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание Видео:Уравнения стороны треугольника и медианыСкачать  Уравнения сторон треугольникаКак составить уравнение сторон треугольника по координатам его вершин? Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки. Дано: ΔABC, A(-5;1), B(7;-4), C(3;7) Составить уравнения сторон треугольника. 1) Составим уравнение прямой AB, проходящей через 2 точки A и B. Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b: Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7): Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Уравнение длины сторон треугольника
Средняя оценка: 4.7 Всего получено оценок: 133. Средняя оценка: 4.7 Всего получено оценок: 133. Уравнение длин сторон треугольника – это первые вкрапления высшей математики в математику школьного курса. Понимание данной тематики приближает ученика к университетскому уровню, вместе с тем делая более понятной тему функции. Видео:Уравнение прямой и треугольник. Задача про высотуСкачать  ФункцияЧто такое функция? Это зависимость одной величины от другой. В математической функции чаще всего две неизвестных: независимая и зависимая или х и у соответственно. Что это значит? Это значит, что х может принимать абсолютно любое значение, а у будет под него подстраиваться, меняясь в соответствии с коэффициентами функции. Существуют ситуации, когда функция имеет несколько переменных. Зависимая у всегда 1, но факторов, которые влияют на неё может быть несколько. Не всегда такую функцию получается отразить на графике. В лучшем случае графически можно отобразить зависимость у от 2 переменных. Как проще всего представить зависимость у(х)? Да очень просто. Представьте себе избалованного ребенка и богатую любящую мать. Они вместе приходят в магазин и начинают клянчить конфеты. Кто знает, сколько конфет мальчик потребует сегодня? Очень важно понимать, что одному значению функции у, всегда соответствует 1 значение аргумента х. Но, как и с корнями квадратного уравнения, эти значения могут совпадать. Видео:Аналитическая геометрия на плоскости. Решение задачСкачать  Уравнение прямой линииЗачем нам нужно уравнение прямой, если мы говорим об уравнении длин сторон треугольника? Да затем, что каждая из сторон треугольника это отрезок. А отрезок это ограниченная часть прямой. То есть мы можем задать уравнения прямых. А в точках их пересечения ограничить линии, тем самым обрезав прямые и превратив их в отрезки. Уравнение прямой выглядит следующим образом: Видео:Вычисляем высоту через координаты вершин 1Скачать  Уравнение сторон треугольникаНеобходимо найти уравнение длин сторон треугольника с вершинами в точках А(3,7) ; В(5,3); С(12;9) Все координаты положительны, значит, треугольник будет расположен в 1 координатной четверти. Поочередно составим уравнения каждой из линий треугольника.
Из первого уравнения выразим b и подставим во второе. Подставим значение а и найдем b. Составим уравнение прямой.
🌟 ВидеоВычисление медианы, высоты и угла по координатам вершинСкачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  найти уравнение высоты треугольникаСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Вычисляем угол через координаты вершинСкачать  Длина медианы треугольникаСкачать  Даны координаты вершин треугольника АВС.Скачать  найти уравнения биссектрис углов между прямымиСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Нахождение длины отрезка по координатамСкачать  | ||
