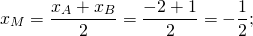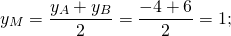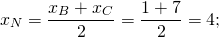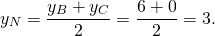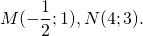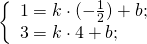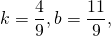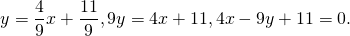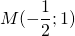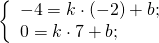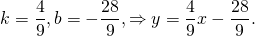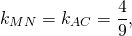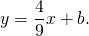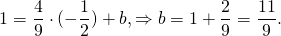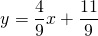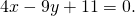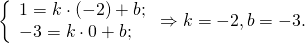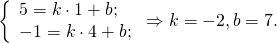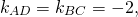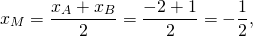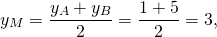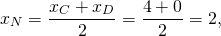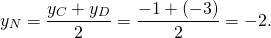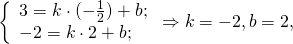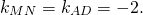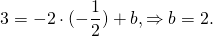Уравнение сторон трапеции по координатам (8 видео)

записать уравнение сторон трапеции с вершинами а( -2,2) b( -1,2) c(3,4) d(6,2) высшая математика

С высшей математикой тут явно перебор.
Это четыре прямые проходящие через соответствующие соседние вершины и имеющие область определения ограниченную координатой Х точек вершин. Попробуй сама их вывести. Это не сложно, если вспомнить уравнение прямой на плоскости проходящей через две заданные точки.

Чего-то вы напутали с координатами. Вот что получилось при построении (смотрите картинку). На трапецию никак не тянет.

Содержание

Уравнение средней линии
Стороны трапеции
Свойства
💡 Видео

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Видео:№974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3; 1). Напишите уравненияСкачать

Стороны трапеции

Видео:Уравнения стороны треугольника и медианыСкачать

Свойства

Трапеция является фигурой с двумя параллельными противоположными сторонами, при этом все четыре стороны могут быть разной длины. Параллельные стороны b и d называются меньшим и большим основанием трапеции, a и c – боковыми сторонами. Зная стороны трапеции, можно найти все характеризующие ее параметры. Периметр трапеции, зная стороны, представляет собой их сумму. P=a+b+c+d

Высота трапеции является перпендикуляром, соединяющим два основания, и может быть проведена в любой их точке, но удобнее всего это делать из вершины углов при меньшем основании, так как тогда образуется прямоугольный треугольник, из которого выводится формула. (рис.103.1) h=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон, и равный полусумме оснований. (рис.103.2) m=(b+d)/2

Площадь трапеции равна произведению ее высоты на среднюю линию. Чтобы найти площадь трапеции через стороны, необходимо развернуть эту формулу до ее истоков, заменив неизвестные переменные. S=hm=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )*(b+d)/2

Если в трапецию можно вписать окружность (а это возможно, если противоположные стороны в сумме дают одно и то же число), то радиус вписанной окружности будет равен половине высоты, или половине квадратного корня из произведения меньшего основания на большее, с учетом условия для окружности. (рис.103.3) r=h/2=√bd/2

Описать окружность можно только вокруг равнобокой трапеции, и если она является таковой, то радиус описанной окружности будет равен радиусу окружности, описанной вокруг треугольника, образованного диагональю. (рис.103.4) R=(abd_1)/√((a+b+d_1)(a+b)(a+d_1)(b+d_1))

Диагонали трапеции рассчитываются по формулам, приведенным через теорему Пифагора в треугольниках, образованных высотой и диагоналями. d_1=√(c^2+db d(c^2-a^2 )/(d-b)) d_2=√(a^2+db (b(c^2-a^2))/(d-b))