Уравнение сторон прямоугольного равнобедренного треугольника

Видео:Равнобедренный треугольник. 7 класс.Скачать

Равнобедренный прямоугольный треугольник – площадь, длина основания, свойства

И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Определение

Равнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны.

Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.

Рис. 1. Равнобедренный прямоугольный треугольник

Видео:Уравнения стороны треугольника и медианыСкачать

Свойства

Поговорим подробнее о свойствах и формулах. Не совсем ясно, как будут пролегать высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой.

В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами.

Рис. 2. Высота прямоугольного равнобедренного треугольника

Если к гипотенузе прямоугольного равнобедренного треугольника провести высоту, то она разделит треугольник на два, равных между собой, равнобедренных прямоугольных треугольника.

Теорема Пифагора для равнобедренного треугольника выглядит немного более упрощенной:

Квадрат гипотенузы равен удвоенному квадрату катета. Это значительно упрощает решение.

Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника.

Через гипотенузу можно найти катет через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45.

Рис. 3. Углы прямоугольного равнобедренного треугольника

Разберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам.

При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны. Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.е. 90 градусов, разделить пополам. Получается, что каждый из углов при гипотенузе прямоугольного равнобедренного треугольника будет равен 45 градусам.

Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным.

Из этого же свойства проистекает равенство синусов и косинусов всех острых углов между собой, а так же равенство тангенсов и котангенсов.

То есть, синус любого острого угла треугольника равен косинусу любого острого угла треугольника и равен $$<sqrtover2>$$. Тангенс любого острого угла треугольника равен котангенсу любого острого угла треугольника и равен 1.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Что мы узнали?

Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника. А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике. Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.

Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».

Видео:Найдите гипотенузу равнобедренного прямоугольного треугольника, площадь которого равна 1Скачать

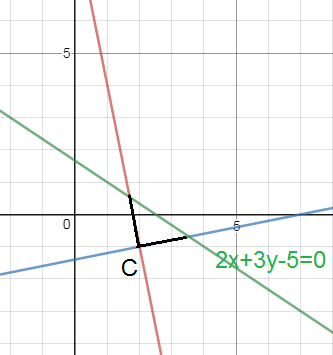
Составить уравнение катетов прямоугольного равнобедренного треугольника

УСЛОВИЕ:

Помогите решить, пожалуйста. Составить уравнения катетов прямоугольного треугольника, зная уравнение гипотенузы 2х+3у-5=0 и вершину прямого угла С(2;-1).

РЕШЕНИЕ ОТ sova ✪ ЛУЧШЕЕ РЕШЕНИЕ

Так и есть по ответам, треугольник прямоугольный равнобедренный.

Угловой коэффициент гипотенузы
k_(гипотенузы)=-2/3

Пусть угловой коэффициент одного катета
k_(1)

Формула тангенса разности двух углов

tg( α – β ) =(tg α -tg β )/(1+tg α *tg β )

((-2/3) -k_(1) )/(1+(-2/3) *k_(1) )=1
находим k_(1) и уравнение прямой первого катета, подставив координаты точки С в уравнение
y=k_(1)x+b

Так как катеты взаимно перпендикулярны, то угловой коэффициент второй прямой k_(2)=-1/k_(1)

Добавил vk492871866 , просмотры: ☺ 449 ⌚ 2019-04-19 15:17:02. математика 1k класс

Решения пользователей

Написать комментарий

Делим обе части равенства на π

и умножаем на 4

+pi k, k in Z
Можно правую часть записать в виде двух ответов:

x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].

x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]

[b]x=-5 – наибольшее отрицательное [/b]

О т в е т. x=1+8n in Z или x=3+ 8n, n in Z

корни чередуются так:

. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .

[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)

a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член

4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0

5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.

∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.

складываем оба равенства:

2* ∠ А=126 градусов.

По формулам приведения:

sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1

sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1

sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z

Найдем корни, принадлежащие указанному отрезку с помощью неравенства:

-286 ° ≤ 90 ° +360 ° *k ≤ 204 °

-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °

-376 ° ≤ 360 ° *k ≤ 114 °

Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]

Значит, указанному отрезку принадлежат два корня:

x=90 ° +360 °* ([green]-1[/green])=-270 °

x=90 ° +360 °*[red]0[/red]=90 °

7. KT- средняя линия трапеции:

Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)

Высоты треугольников АКО и СОК равны половине высоты трапеции

S_( Δ АКО)+S_( Δ COK)=44

S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=

О т в е т. [b]176[/b]

B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

3.4 Прямая на плоскости

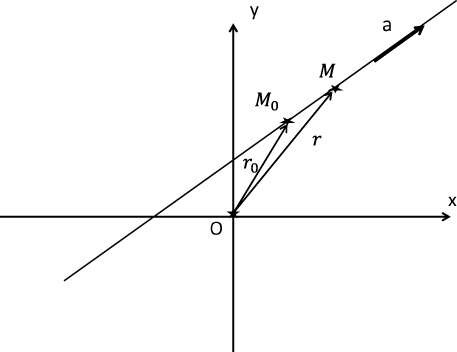
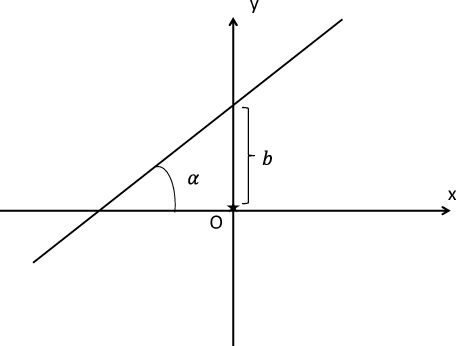
Для прямой на плоскости мы приведем несколько уравнений. В зависимости от задачи удобнее использовать то или иное уравнение и довольно часто требуется перейти от уравнения прямой в одной форме к уравнению, описывающему прямую в другой форме.

&nbsp

Рис 3: Прямая определяется точкой, через которую она проходит, и направляющим вектором.

&nbsp

Рис 4: Прямая: фиксирован угловой коэффициент и отрезок, отсекаемый на оси $y$.

Проведем через точку $(-1,,1)$ прямую, параллельную прямой $2x+3y+7=0$. Эта прямая будет иметь уравнение $2x+3y+C=0$, где число $C$ подлежит определению (коэффициенты перед $x,,y$ определяют наклон прямой и если мы возьмем их, как в исходной прямой, получим параллельную прямую). Подставляя точку в искомую прямую, получим уравнение для $C$: $-2+3+C=0$, так что $C=-1$ и искомое уравнение прямой: $2x+3y-1=0$.

Пусть задано общее уравнение прямой на плоскости. Перепишите его в виде нормального уравнения прямой.

Решение типовых задач.

Написать уравнения прямой в общем виде и с угловым коэффициентом, если прямая проходит через точки $ extbf (2,3)$ и $ extbf (4,-6)$.

Для написания уравнения искомой прямой воспользуемся формулой (
ef

). Подставляя в нее вместо $(x_0,y_0)$ координаты точки $ extbf $, а вместо $(x_1,y_1)$ – координаты точки $ extbf $, получим [ frac =frac . ] или [ frac =frac . ] С помощью несложных элементарных преобразований (домножения на наименьший общий знаменатель, переноса в левую часть и приведения подобных слагаемых), получим уравнение в общем виде: [ 2y + 9x -24 = 0 ] Теперь приведем это уравнение к виду уравнения прямой с угловым коэффициентом: [ y = 12 – frac . ]

Две стороны параллелограмма заданы уравнениями $2x+5y+6=0$ и $x-3y=0$. Известны координаты одной из вершин параллелограмма – $ extbf (4;-1)$. Написать уравнения двух других сторон параллелограмма.

В параллелограмме противоположные стороны параллельны, значит исходная задача сводится к построению прямых, параллельных данным и проходящих через заданную точку. Построим прямую, параллельную прямой $2x+5y+6=0$. Ее уравнение будет иметь вид $2x+5y+C=0$. Значение $ extbf $ определим, подставив в это уравнение координаты точки $ extbf $: $2 cdot 4 + 5 cdot (-1) + C=0$. Следовательно, $ extbf $ и искомое уравнение стороны есть [ 2x+5y-3=0 ] Аналогичным образом, подставляя в уравнение $x-3y+C=0$ координаты точки $ extbf $: $4 -3 cdot (-1)+C=0$, получим уравнение другой стороны параллелограмма: [ x-3y-7=0. ]

Проверить, что прямые [ y = 3x-1, x+y-7=0, x-7y=7 ] служат сторонами равнобедренного треугольника.

Выяснить являются ли перпендикулярными прямые $3x-2y=0$ и $-4x-6y+3=0$.

Приведем уравнения к виду уравнений с угловыми коэффициентами: [ y = frac , y = -frac +frac ] Тогда угловой коэффициент первого уравнения $k_1=frac $, второго – $k_1=-frac $. Проверим условие ортогональности, согласно которому $k_1cdot k_2=-1$. В нашем случае имеем $k_1cdot k_2=frac cdot -frac = -1$ . Это означает, что заданные прямые перпендикулярны.

Найти расстояние от прямой $frac =frac $ до точки $P(2,-1)$.

Приводя исходное уравнение к общему виду, получим [ 3x+4y+1 =0. ] Расстояние от точки $P(2,-1)$ до прямой вычислим по формуле [ p=frac > = frac . ]

1. Составить уравнение прямой, проходящей через точку $ M(-2,1)$ и параллельной прямой [ frac =frac . ]

2. Составить уравнение прямой, проходящей через точку $M(-2,1)$ и перпендикулярной прямой [ frac =frac . ]

3. Найти угол между прямыми [ frac =frac , quad frac =frac . ]

4. Составить уравнение биссектрисы острого угла между прямыми $3y=4x$ и $5x+12y=6$.

5. Написать уравнение прямой, удаленной на 5 от прямой $12x+5y=39$.

6. Основания трапеции лежат на прямых [ 2x+sqrt y-24=0, quad 2x+sqrt y+6=0. ] Найти ее высоту.

7. Проверить, что прямые $2x+frac y-15=0$ и $frac x-5y+30=0$ касаются одной и той же окружности с центром в начале координат и вычислить ее радиус.

8. На расстоянии 5 от точки $M(4,3)$ провести прямую, отсекающую равные отрезки на осях координат.

9. На оси $y$ найти точку, равноудаленную от начала координат и от прямой $3x-4y=12=0$.

10. Через точку пересечения прямых $2x-y=2$ и $x+y=1$ провести прямую, параллельную прямой $y=3x-2$.

11. Составить уравнения катетов прямоугольного равнобедренного треугольника, зная уравнение гипотенузы $y=3x+5$ и вершину прямого угла $M(4,-1)$.

12. Вычислить координаты вершин ромба, если известны уравнения двух его сторон $2x-5y-1=0$ и $2x-5y-34=0$ и уравнение одной из диагоналей $x+3y-6=0$.

13. Найти уравнения сторон треугольника, зная одну из его вершин $A(3,4)$ и уравнения двух высот $7x-2y=1$ и $2x-7y=6$.

14. Через точку $M(0,1)$ провести прямую так, чтобы ее отрезок, заключенный между двумя данными прямыми $x-3y+10$ и $2x+y-8=0$, делился в этой точке пополам.

15. Составить уравнения сторон треугольника, зная одну из его вершин $A(-4,2)$ и уравнения двух медиан $3x-2y+2=0$ и $3x+5y-12=0$.

16. Даны две противоположные вершины квадрата $A(-5,2)$ и $C(3,-4)$. Составить уравнения его сторон.

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Ответ или решение 1

1. Найдем расстояние l между точкой C(3; -1) и произвольной точкой M(x; y), лежащей на заданной прямой:

• 3x + 2y – 6 = 0;
• 2y = 6 – 3x;
• y = 3 – 1,5x;

• l^2 = (x – 3)^2 + (y + 1)^2;
• l^2 = (x – 3)^2 + (3 – 1,5x + 1)^2;
• l^2 = (x – 3)^2 + (4 – 1,5x)^2;
• l^2 = x^2 – 6x + 9 + 16 – 12x + 2,25x^2;
• l^2 = 3,25x^2 – 18x + 25;
• l^2 = 13/4 * x^2 – 18x + 25;
• l^2 = 13/4(x^2 – 72/13 * x + 100/13);
• l^2 = 13/4((x – 36/13)^2 – 1296/13 + 100/13);
• l^2 = 13/4((x – 36/13)^2 – 1296/13^2 + 1300/13^2);
• l^2 = 13/4((x – 36/13)^2 + 4/13^2);
• l^2 = 13/4(x – 36/13)^2 + 1/13.

2. Высота CH равнобедренного прямоугольного треугольника ABC (http://bit.ly/2MLdSeb), проведенная к гипотенузе AB, равна половине гипотенузы AB и наименьшему значению l:

3. А длина катетов AC и BC в √2 раз больше высоты CH:

отсюда получим уравнение для координат вершин A и B:

• l^2 = 2/13;
• 13/4(x – 36/13)^2 + 1/13 = 2/13;
• 13/4(x – 36/13)^2 = 1/13;
• (x – 36/13)^2 = 4/13^2;
• (x – 36/13)^2 = (2/13)^2;
• x – 36/13 = ±2/13;
• x = 36/13 ± 2/13;
• x = (36 ± 2)/13;

1) x = (36 – 2)/13 = 34/13;

y = 3 – 1,5x = 3 – 3/2 * 34/13 = 39/13 – 51/13 = -12/13;

2) x = (36 + 2)/13 = 38/13;

y = 3 – 1,5x = 3 – 3/2 * 38/13 = 39/13 – 57/13 = -18/13.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Все формулы для треугольника

Видео:Прямоугольный равнобедренный треугольникСкачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:Геометрия Найдите катеты прямоугольного равнобедренного треугольника, гипотенуза которого равна cСкачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

🔥 Видео

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Площадь равнобедренного треугольникаСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

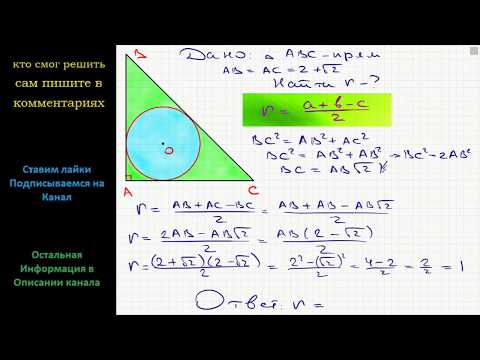
Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Уравнение прямой и треугольник. Задача про высотуСкачать

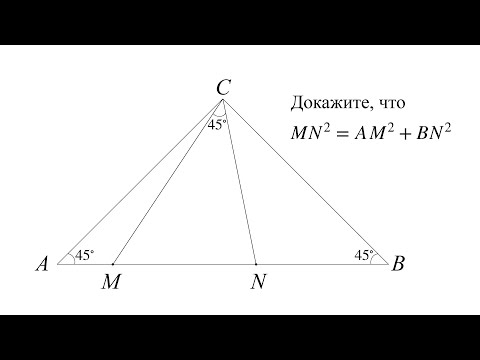
Доказать равенство для равнобедренного прямоугольного треугольникаСкачать

ЕГЭ математика 2021: Все задачи на равнобедренный треугольник (6 задание)Скачать