Уравнение стокса для скорости осаждения частиц (5 видео)

Лако-красочные материалы — производство

Содержание

Технологии и оборудование для изготовления красок, ЛКМ
Условия соблюдения закона Стокса при седиментации дисперсных систем
Как определить вязкость жидкости методом Стокса?
Что такое вязкость
Движение тела в жидкой среде
Формула вязкости
Дифференциальное уравнение осаждения частицы под действием силы тяжести.
💡 Видео

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Условия соблюдения закона Стокса при седиментации дисперсных систем

Рассмотрим условия, при которых соблюдаются закономерности седиментации, описываемые уравнениями (IV.7) и (IV.8). Эти соотношения справедливы, если частицы дисперсной фазы осаждаются независимо друг от друга, что может быть только в разбавленных системах. При осаждении в концентрированных системах происходят столкновения частиц, в результате которых малые частицы тормозят движение более крупных, а крупные ускоряют движение мелких частиц. В итоге происходит более медленное коллективное осаждение, и, кроме того, скорость осаждения частиц уменьшается под действием возникающего в этом случае встречного потока жидкости со дна сосуда, в котором находится дисперсная система.

Обычно частицы в дисперсных системах с твердой дисперсной фазой имеют неправильную форму. При свободном оседании частица несферической формы ориентируется в направлении движения таким образом, чтобы создавалось максимальное сопротивление движению, что уменьшает скорость осаждения. При расчете по уравнению (IV.6) коэффициента трения для частиц, линейные размеры которых по разным направлениям различаются незначительно, можно воспользоваться фактором формы, равным отношению площадей поверхностей сферической частицы scф и реальной частицы s, имеющих одинаковые объемы:

Так как всегда Sc$ 2 зависимость силы трения от скорости движения возрастает в большей степени, чем согласно закону Стокса. При развитой турбулентности (Re>500) сила трения пропорциональна квадрату скорости движения частиц. Неправильная форма частиц способствует турбулентности нх движения при меньших скоростях. Таким образом, закон Стокса выполняется, если скорость осаждения частиц не превышает определенного значения. Уменьшение скорости достигается увеличением дисперсности частиц, вязкости и плотности среды [см. уравнение (IV.7)].

Закон Стокса предполагает наличие внутреннего трения, или вязкого трения, когда граница (поверхность) движения частицы относительно среды находится внутри дисперсионной среды, вязкость которой определяет коэффициент трения. Внутреннее трение обычно преодолевается при движении жидких или твердых частиц в газообразной или жидкой среде, что обусловлено значительным межфазиым взаимодействием. Если межфазное взаимодействие мало, граница (поверхность) движения частицы относительно среды может совпадать с поверхностью раздела фаз и трение оказывается внешним. Это приводит к возникновению скольжения, ускоряющему движение частицы. В реальных системах нет резкой границы перехода от трения скольжения к вязкому трению; в промежуточной переходной области необходимо учитывать закономерности, характерные для вязкого трения и трения скольжения. Скольжение можно учесть, вводя дополнительный множитель в уравнение Стокса (IV.6):

FTP ==! (лщги 3tl + rT)c (IV. 17)

Где Т)с — коэффициент внешнего трения (скольжения).

При отсутствии скольжения цс=(» и формула (IV. 17) переходит в уравнение Стокса.

Применимость закона Стокса ограничивается также дисперсностью частиц. Большие частицы (>100 мкм) могут двигаться ускоренно, и тогда для определения скорости их движения нельзя пользоваться уравнениями (IV.5), (IV.7) и (IV.8). Кроме того, быстрое движение больших частиц может вызвать турбулентный режим потока, при котором также перестает соблюдаться закон Стокса. Очень малые частицы — ультрамикрогете — рогенные ( соотношение между силой трения и радиусом отвечает выводам из молеку- лярно-кинетической теории (/чр

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Как определить вязкость жидкости методом Стокса?

Формулу определения вязкости Стокс вывел ещё в 1851 году.

Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.

Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.

Всё это и конкретные методы описаны далее в статье.

Содержание статьи

Видео:Осаждение в поле силы тяжести | Лекция ПАППСкачать

Что такое вязкость

Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.

Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.

По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.

Движение тела в жидкой среде

Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.

Механизм №1 — За твердым телом нет вихрей

Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.

В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).

Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.

Механизм №2 — При движении тела образуются вихри

Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.

Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.

Сила сопротивления

В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.

Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:

где μ – вязкость жидкости;
r – радиус шарика;
υ – скорость равномерного движения шарика.

Условие использования формулы

Существует несколько ограничений для применения формулы Стокса.
1. вязкая среда не ограничена стенками и находится в покое
2. скольжений на границах с твердым телом нет
3. движение жидкости ламинарное
4. радиус круглого тела намного больше, чем длина среднего пробега молекул жидкой среды

Формула вязкости

Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
F_T – сила тяжести;
F_A – сила Архимеда (выталкивающая сила);
T_C – сила лобового сопротивления.

Для круглого шарика сила тяжести будет:

где r –радиус шара;
ρ – плотность шара;
ρ₀ – плотность жидкости;
g – ускорение свободного падения;
υ – скорость равномерного движения шарика;
μ – вязкость жидкости.

В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.

При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:

или подставляя формулы

таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле

Определение вязкости методом Стокса

Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.

На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.

Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.

Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.

Учитывая, что скорость это отношения длины пути ко времени, т.е.:

и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса

Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.

При падении шара радиусом r в трубе радиусом R₀ и высотой h формула будет выглядеть

Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом Стокса требует значения таких параметров, как:
плотность материала шарика;
плотность жидкости;
радиус шарика;
радиус сосуда;
скорость движения шарика.

Видео про методы определения вязкости

Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.

Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.

Но независимо от метода общими остаются:
1. результат измерение не должен зависеть от линейных размеров вискозиметра.
2. не должно быть пристеночного скольжения жидкости.
3. поток жидкости в используемом вискозиметре должен быть ламинарным.

Видео:Определение коэффициента вязкости жидкости методом СтоксаСкачать

Дифференциальное уравнение осаждения частицы под действием силы тяжести.

Лекция 5. гидромеханические процессы

Неоднородные системы и методы их разделения

Неоднородные, или гетерогенные системы, состоят из двух или нескольких фаз. Любая неоднородная бинарная система состоит из дисперсной (внутренней) фазы и дисперсионной среды (внешней) фазы, в которой распределены частицы дисперсной фазы. В зависимости от физического состояния фаз различают суспензии, эмульсии, пены, пыли, дымы и туманы.

Суспензии — неоднородные системы, состоящие из жидкости и взвешенных в ней твердых частиц. В зависимости от размеров твердых частиц суспензии условно подразделяют на грубые (с размером частиц более 100 мкм), тонкие (с размером частиц 0,5…100,0 мкм) и коллоидные растворы (с размером частиц менее 0,1…0,5 мкм).

Пыли — системы, состоящие из газа и распределенных в нем твердых частиц размерами 3…70 мкм.

Дымы — системы, состоящие из газа и распределенных в нем твердых частиц размерами 0,3…3,0 мкм, они образуются при горении.

Туманы — системы, состоящие из газа и распределенных в нем капель жидкости размерами 0,3…3,0 мкм, образовавшихся в процессах конденсации.

Пыли, дымы и туманы представляют собой аэрозоли.

Эмульсии — системы, состоящие из жидкости и распределенных в ней капель другой жидкости, не растворяющейся в первой.

Пены— системы, состоящие из жидкости и распределенных в ней пузырьков газа. Для эмульсий и пен характерна возможность перехода дисперсной фазы в дисперсионную среду и наоборот, этот переход, возможный при определенном массовом соотношении фаз, называют инверсией фаз.

Осаждение – процесс разделения неоднородных смесей на фракции, при котором взвешенные в жидкости или газе твердые или жидкие частицы отделяются от сплошной фазы под действием силы тяжести, центробежных сил или электростатических сил.

Отстаивание – это осаждение, происходящее под действием силы тяжести.

Материальный баланс гидромеханических процессов. Пусть подлежащая разделению неоднородная система состоит из вещества а (дисперсионной фазы) и взвешенных в ней частиц вещества b (дисперсной фазы). Обозначим , , — масса исходной смеси, осветленной жидкости и получаемого осадка, кг; , , — содержание вещества b в исходной смеси, осветленной жидкости и осадке, массовые доли.

При отсутствии потерь уравнения материального баланса имеют вид:

по общему количеству веществ

, (1)

по дисперсной фазе (веществу b):

. (2)

Решив совместно уравнения (1) и (2), определяем массу осветленной жидкости и массу осадка :

, (3)

. (4)

Кинетика осаждения

Дифференциальное уравнение осаждения частицы под действием силы тяжести.

Рассмотрим движение частицы произвольной формы под действием силы тяжести. Если плотность частицы , а жидкости , то на частицу действуют сила тяжести G и подъемная (архимедова) сила S, направленная в сторону, обратную направлению силы тяжести (рис. 1):

, (5)

. (6)

где l — наиболее характерный размер частицы, м; — коэффициент, зависящий только от формы частицы.

Под действием разности этих сил частица перемещается в жидкости, при этом на частицу со стороны жидкости действует сила трения, определяемая законом Ньютона, которая зависит от площади поверхности частицы

, (7)

где — коэффициент, учитывающий форму частицы; — коэффициент вязкости жидкости, Па×с; — изменение скорости движения жидкости в направлении, нормальном к поверхности частицы.

На основании второго закона механики для рассматриваемого случая равнодействующая сила равна

. (8)

Равенство (8) представляет собой дифференциальное уравнение осаждения частицы под действием силы тяжести. При его выводе не учитывались инерционные силы, что допустимо для установившегося ламинарного движения. Уравнение (8) не может быть решено в общем виде, поэтому для определения скорости осаждения частиц под действием силы тяжести необходимо прибегнуть к теории подобия.

Таким образом, из дифференциального уравнения (8) получаем уравнение подобия, описывающее процесс осаждения частиц,

. (14)

Установлены следующие режимы движения частицы в жидкости в процессе осаждения: ламинарный (Re 500).

Для каждого режима движения найдены зависимости

для ламинарного режима (при Re

, (15)

для переходного режима (при l,85 500 или >83000):

. (17)

Зная область осаждения, можно по найденному с помощью уравнений (15) – (17) значению числа Рейнольдса рассчитать скорость осаждения частицы в жидкости под действием силы тяжести:

. (18)

Закон Стокса. Рассмотрим процесс осаждения частицы сферической формы диаметром d при ламинарном движении. Тогда скорость осаждения равна:

. (20)

Уравнение (20) выражает закон Стокса: при ламинарном движении скорость осаждения шарообразных частиц пропорциональна квадрату их диаметра, разности плотностей частиц и среды и обратно пропорциональна вязкости среды.

Скорость осаждения u_о частиц неправильной формы меньше, чем скорость осаждения шарообразных частиц. Чтобы ее рассчитать, значение скорости осаждения u_о для шарообразных частиц необходимо умножить на поправочный коэффициент , называемый коэффициентом формы,

. (21)

Значения коэффициента формы определяют опытным путем (для частиц округлой формы — 0,77, для угловатых частиц — 0,66, для продолговатых частиц — 0,58 и для пластинчатых частиц — 0,43). Кроме того, при расчете скорости осаждения частиц нешарообразной формы в соответствующие уравнения для определения скорости следует подставлять эквивалентный диаметр.

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Аr для всех режимов осаждения,

. (22)

При малых значениях Аr вторым слагаемым в знаменателе можно пренебречь, и уравнение (22) превращается в уравнение (15), соответствующее области действия закона Стокса; при больших же значениях Аr пренебречь можно уже первым слагаемым в знаменателе, и уравнение (22) превращается в уравнение (17), отвечающее турбулентной области.

Сила сопротивления R (н) жидкости движущейся в ней частице может быть выражена уравнением закона сопротивления

, (23)

где z — коэффициент сопротивления жидкости; S — площадь проекции частицы на плоскость, перпендикулярную направлению его движения, м 2 ; — плотность жидкости, кг/м 3 ; — скорость частицы, м/с.

Отношение R/S представляет собой перепад давлений (Н/м 2 ), преодолеваемый движущееся частицей. Поэтому, решив уравнение (23) относительно z, можно установить, что коэффициент сопротивления z пропорционален критерию Эйлера (z отличается от Еu лишь множителем 2).

На рис. 2 представлена зависимость z от критерия Рейнольдса Re при движении шарообразных частиц диаметром d. Этот диаметр и является определяющим размером в критерии Re.

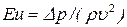
Из него видно, что существуют три различных режима движения, каждому из которых соответствует определенный характер зависимости z от Re:

ламинарный режим (область действия закона Стокса) приблизительно при Re 6 ;> Re >

const. (26)

Подстановка в уравнение (23) каждого из приведенных выше уравнений для z показывает, что при ламинарном режиме сила сопротивления пропорциональна скорости в первой степени, т. е. R

, при переходном режиме R – 1,4 , а при автомодельном режиме R

2 .

Приведенный расчет скорости свободного осаждения u_о относится к режиму, при котором осаждающиеся частицы практически не оказывают влияния на движение друг друга. В пищевой промышленности процессы осаждения очень часто проводятся в условиях, когда оседающие частицы могут влиять на движение друг друга. При значительной концентрации твердых частиц в жидкости происходит стесненное осаждение, скорость которого меньше, чем свободного, вследствие трения и соударений между частицами.

Рассмотрим процесс отстаивания неоднородной системы, при котором наблюдается постепенное увеличение концентрации частиц в аппарате по направлению сверху вниз (рис. 3).

При этом в аппарате образуются четыре зоны: зона 1 — слой осадка; зона 2 – сгущенная суспензия; зона 3 – свободного осаждения; зона 4 – осветленная жидкость.

В зоне сгущенной суспензии происходит стесненное осаждение частиц, сопровождающееся трением и взаимными столкновениями. При этом более мелкие частицы тормозят движение более крупных, а частицы больших размеров увлекают за собой мелкие частицы, ускоряя их движение. В результате наблюдается тенденция к сближению скоростей осаждения частиц различных размеров; возникает коллективное, или солидарное, осаждение частиц с близкими скоростями в каждом сечении аппарата.

Уменьшение скорости частиц по мере приближения к днищу аппарата объясняется тормозящим действием жидкости, вытесняемой осаждающимися частицами и движущейся в обратном направлении.

При этом высота отдельных зон изменяется во времени до момента полного расслоения неоднородной системы на осадок и осветленную жидкость. Это является следствием изменения скорости отстаивания u_{о с}_т во времени t (рис. 4).

В начале отстаивания осаждаются преимущественно более крупные частицы, вызывающие наиболее интенсивное обратное движение жидкости. Однако по мере уменьшения концентрации этих частиц тормозящее влияние обратного тока жидкости ослабевает и скорость отстаивания возрастает (отрезок aб на рис. 4) до момента установления динамического равновесия между действующей силой и силой сопротивления жидкости. В последующий период времени совместное осаждение частиц происходит с постоянной скоростью (отрезок бв на рис. 4). На завершающей стадии процесса происходит уплотнение осадка, т. е. частицы располагаются близко друг к другу и вытеснение жидкости становится затруднительным. При этом процесс отстаивания протекает с уменьшающейся скоростью (отрезок вг на рис. 4).

Скорость стесненного осаждения меньше скорости свободного осаждения. Это объясняется тем, что при стесненном осаждении частицы испытывают не только большее сопротивление жидкости, но и добавочное сопротивление, обусловленное трением и соударениями частиц.

Интерполяционное уравнение, применимое для всех областей осаждения, имеет вид

. (27)

Определив по уравнению (27) критерий , находят скорость стесненного осаждения u_о._ст_.

Отстойники

Отстаивание проводят в аппаратах, называемых отстойниками или сгустителями. Различают аппараты периодического, непрерывного и полунепрерывного действия, причем непрерывно действующие отстойники, в свою очередь, делятся на одноярусные, двухъярусные и многоярусные.

Периодически действующие отстойники представляют собой низкие емкости без перемешивающих устройств. Такой отстойник заполняется суспензией, которая остается в состоянии покоя в течение определенного времени, необходимого для оседания твердых частиц на дно аппарата. После этого слой осветленной жидкости сливают через сифонную трубку, расположенную выше уровня осевшего осадка. Последний, обычно представляющий собой подвижную текучую густую жидкую массу, выгружают вручную через верх аппарата или удаляют через нижний спусковой кран.

Скорость отстаивания существенно зависит от температуры, с изменением которой изменяется вязкость жидкости, причем скорость осаждения обратно пропорциональна вязкости, а последняя уменьшается с увеличением температуры.

Одноярусный отстойник непрерывного действия со скребковой мешалкой (рис. 5) представляет собой цилиндрический резервуар 1 с коническим днищем и внутренним кольцевым желобом 2. В резервуаре установлена мешалка 3 с наклонными лопастями, на которых имеются скребки 4 для непрерывного перемещения осаждающегося материала к разгрузочному отверстию 7. Одновременно скребки слегка взбалтывают осадок, способствуя этим более эффективному его обезвоживанию. Мешалка вращается медленно, чтобы не нарушать процесс осаждения. Исходная суспензия непрерывно подается через трубу 5 в середину резервуара. Осветленная жидкость переливается в кольцевой желоб 2 и удаляется через штуцер 6. Осадок удаляется из резервуара через разгрузочное отверстие 7.

Одноярусные отстойники со скребковыми мешалками обладают следующими достоинствами: в них достигается равномерная плотность осадка, имеется возможность регулировать ее изменяя производительность, обеспечивается более эффективное обезвоживание осадка вследствие легкого взбалтывания его мешалкой. К недостаткам этих аппаратов следует отнести их громоздкость.

Расчет отстойников. Производительность отстойника по осветленной жидкости (м 3 /с),

, (30)

где — скорость потока жидкости вдоль отстойника, м/с; b – ширина отстойника прямоугольного сечения, м; h – высота слоя осветленной жидкости, м.

Время прохождения t (с) суспензией отстойника

, (31)

где l – длина отстойника прямоугольного сечения, м.

За это же время частицы, осаждающиеся со скоростью , (м/с), должны пройти наибольший путь h (м). Следовательно, время отстаивания равно

. (32)

Приравнивая правые части уравнений (31) и (32) и подставляя вместо его значение из уравнения (30), получим

, (33)

откуда производительность отстойника по осветленной жидкости составит

, (34)

где F — поверхность отстойника в плане, м 2 .

Уравнение (34) показывает, что производительность отстойника не зависит от его высоты, а зависит от скорости и поверхности осаждения. Поэтому отстойники имеют значительную поверхность осаждения при небольшой высоте, которая обычно не превышает 1,8…4,5 м, а для отстойников очень больших диаметров – не более 7 м.

Необходимую поверхность осаждения F (м 2 ) находим из выражения

. (35)

В инженерных расчетах поверхность отстойника, определенную по уравнению (37), увеличивают на 30…35 %, т. к. при выводе уравнения (35) допускалось, что в отстойнике отсутствуют застойные зоны и не происходит вихреобразования жидкости, вызванного неравномерностью осаждения частиц.

Фильтрование

Процесс фильтрации основан на задержании твердых взвешенных частиц фильтрующими перегородками, способными пропускать только жидкость и задерживать частицы твердой фазы. При прохождении суспензии через пористую перегородку за счет разности давлений до и после перегородки жидкая фаза проходит через поры перегородки и собирается в виде освобожденного от твердых примесей фильтрата, а твердые частицы задерживаются на поверхности фильтрующей перегородки, образуя слой осадка (рис. 1).

Движущей силой фильтрации является разность давлений на входе в фильтр, состоящий из фильтрующей перегородки и слоя осадка, и на выходе из него. Разность давлений по обе стороны фильтровальной перегородки создают разными способами, в результате чего различают процесс фильтрования при постоянной разности давлений и процесс фильтрования при постоянной скорости.

Процесс фильтрования при постоянной разности давлений происходит, если пространство над суспензией сообщается с источником сжатого газа или пространство под фильтровальной перегородкой присоединяют к источнику вакуума так, что давление поддерживается постоянным. В этом случае скорость процесса фильтрования уменьшается в связи с увеличением сопротивления слоя осадка возрастающей толщины.

Процесс фильтрования при постоянной скорости осуществляется при подаче суспензии на фильтр поршневым насосом, производительность которого при данном числе оборотов электродвигателя постоянна. В этом случае разность давлений увеличивается за счет повышения сопротивления слоя осадка возрастающей толщины.

Различают также процесс фильтрования при переменных разности давлений и скорости, когда суспензию транспортируют на фильтр центробежным насосом, производительность которого при данном числе оборотов электродвигателя уменьшается при возрастании сопротивления осадка, что обусловливает повышение разности давлений.

В процессе фильтрования твердые частицы могут отлагаться на фильтровальной перегородке в виде осадка – этот процесс разделения суспензии называют фильтрованием с образованием осадка.

Процесс, когда твердые частицы проникают в поры фильтровальной перегородки и задерживаются там, не образуя осадка, называют фильтрованием с закупориванием пор.

Возможен также промежуточный вид фильтрования, когда твердые частицы проникают в поры фильтровальной перегородки и образуют на ней слой осадка. Застрявшие частицы будут уменьшать эффективное сечение поры, и вероятность задерживания в ней последующих твердых частиц увеличится. Возможен случай, когда отдельная частица полностью закупоривает пору и делает ее непроходимой для других частиц. Наконец, небольшая по сравнению с порами твердая частица может, несмотря на это, не войти в пору и остаться на поверхности фильтровальной перегородки.

Наиболее предпочтительно фильтрование с образованием осадка, когда не происходит закупоривание пор фильтровальной перегородки твердыми частицами с соответствующим увеличением ее сопротивления.

Нежелательно фильтрование с закупориванием пор фильтровальной перегородки, т. к. регенерация ее в данном случае сильно осложняется, а иногда становится невозможной вследствие трудности извлечения твердых частиц из пор.

Для уменьшения гидравлического сопротивления осадка необходимо периодически удалять его с фильтрующей перегородки. Характер и толщина слоя осадка, отлагающегося на поверхности фильтрующей перегородки, являются важными параметрами, определяющими эффективность фильтрации.

Осадки, получаемые на фильтровальной перегородке при разделении суспензий, подразделяют на:

– несжимаемые – получаемые из недеформируемых (кристаллических) частиц; в них пористость, т. е. отношение объема пор к объему осадка, не уменьшается при увеличении разности давлений. Скорость фильтрования суспензий, образующих несжимаемые осадки, растет с увеличением давления на жидкость, а при одном и том же давлении зависит только от толщины слоя осадка.

– сжимаемые – получаемые из деформируемых (аморфных) части, пористость сжимаемых осадков уменьшается, аих гидравлическое сопротивление потоку жидкой фазы возрастает с увеличением разности давлений.

С повышением давления осадок сжимается, поры его уменьшаются и скорость фильтрации снижается. Следовательно, в этом случае скорость фильтрации растет непропорционально разности давлений, а имеет некоторое отставание. Более того, скорость фильтрации при некоторой разности давлений не только не увеличивается, а наоборот, уменьшается вследствие сжатия осадка.

Уравнения фильтрования. Ввиду небольшого размера пор в слое осадка и фильтровальной перегородке, а также малой скорости движения жидкой фазы в порах считают, что фильтрование протекает в ламинарной области. При таком условии скорость фильтрования в каждый данный момент прямо пропорциональна разности давлений, но обратно пропорциональна вязкости жидкости фазы и общему гидравлическому сопротивлению слоя осадка и фильтровальной перегородки.

Основное дифференциальное уравнение фильтрования имеет вид

, (1)

где V — объем фильтрата, м 3 ; S — поверхность фильтрования, м 2 ; t — продолжительность фильтрования, с; Dp — разность давлений, Па; m — вязкость жидкой фазы суспензии, Па×с; R_oc — сопротивление слоя осадка; R_фп — сопротивление фильтровальной перегородки.

В уравнении (1) разность давлений представляет собой движущую силу, а общее сопротивление складывается из сопротивлений осадка (mR_oc) и фильтровальной перегородки (mR_фп). Сопротивление осадка R_oc тем больше, чем меньше пористость осадка и больше удельная поверхность составляющих его твердых частиц; на величину R_oc влияют также размер и форма частиц.

Уравнение фильтрования при постоянной разности давлений. Примем, что процесс фильтрования протекает при постоянной разности давлений (Dр = const) и постоянной температуре (t = const). Тогда все входящие в уравнение (3) величины, за исключением V и t, постоянны. Интегрируя это уравнение в пределах от 0 до V и от 0 до t, получим:

(4)

, (5)

где r_o — удельное объемное сопротивление слоя осадка,м -2 ; x_o – отношение объема осадка к объему фильтрата.

Разделив обе части уравнения (5) на , получим

. (6)

Уравнение (6) показывает зависимость продолжительности фильтрования от объема фильтрата. Решая его относительно V, получим зависимость объема фильтрата от продолжительности фильтрования. Это уравнение применимо к несжимаемым и сжимаемым осадкам, поскольку при Dр = const величины r_о и x_o также постоянны. Из уравнения (3) следует, что при Dр = const по мере увеличения объема фильтрата, а следовательно, и продолжительности фильтрования скорость фильтрования уменьшается.

Уравнение фильтрования при постоянной скорости процесса. Для фильтрования при постоянной скорости производную dV/dt можно заменить отношением конечных величин V/t. Решая уравнение (3) относительно Dр, находим

. (7)

Умножив и разделив первое слагаемое правой части этого уравнения на t и приняв во внимание, что постоянная скорость фильтрования равна , получим

. (8)

Уравнение (8) показывает, что при постоянной скорости фильтрования (W = const) разность давлений возрастает по мере увеличения продолжительности фильтрования. Это уравнение применимо к несжимаемым осадкам; при использовании его для сжимаемых осадков следует иметь в виду зависимость удельного сопротивления осадка от разности давлений.

Уравнение фильтрования при постоянных разности давление и скорости. Такой вид фильтрования осуществим, если чистая жидкость фильтруется сквозь слой осадка неизменной толщины при постоянной разности давлений. Промывку осадка на фильтре способом вытеснения, когда над осадком находится слой промывной жидкости, можно рассматривать как фильтрование промывной жидкости сквозь слой осадка неизменной толщины при постоянных разности давлений и скорости.

Приняв в уравнении (3) вместо эквивалентную этому выражению толщину слоя осадка на фильтре и заменив в нем dV/dt на постоянное значение V/t, при Dр = const найдем

. (9)

Это уравнение дает зависимость объема фильтрата от продолжительности фильтрования, чистой жидкости, в частности промывной жидкости. Поскольку в рассматриваемом случае Dр = const, уравнение (9) применимо для несжимаемых и сжимаемых осадков.

Из основного уравнения фильтрования (3) следует, что при прочих равных условиях скорость фильтрования тем больше и производительность фильтра тем выше, чем меньше объем полученного фильтрата или пропорциональная этому объему толщина слоя осадка на фильтровальной перегородке. Поэтому для повышения производительности фильтра необходимо стремиться к возможно быстрому удалению осадка с фильтровальной перегородки.

Фильтровальные перегородки. Фильтровальная перегородка представляет собой основную часть фильтра. От правильного выбора ее зависят производительность фильтра и чистота получаемого фильтрата. Выбор перегородки основывается на сопоставлении свойств разделяемой суспензии и характеристик различный перегородок. Фильтровальная перегородка должна иметь минимальное гидравлическое сопротивление и обеспечивать хорошую задерживающую способность твердых частиц и получение чистого фильтрата.

Фильтровальные перегородки классифицируются на следующие группы:

— по принципу действия различают поверхностные и глубинные фильтровальные перегородки;

— по материалам, из которых они изготовлены, – хлопчатобумажные, шерстяные, синтетические, стеклянные, керамические и металлические;

— по структуре фильтровальные перегородки подразделяются на гибкие и негибкие.

Поверхностные перегородки отличаются тем, что твердые частицы суспензии при ее разделении в основном задерживаются на их поверхности, не проникая в поры. Глубинные перегородки, которые используются преимущественно для осветления жидкостей, содержащих твердые частицы в небольшой концентрации, характеризуются тем, что частицы суспензии в процессе ее разделения проникают в их поры и задерживаются там.

Гибкие перегородки могут быть металлическими или неметаллическими, негибкие перегородки — жесткими, состоящими из связанных твердых частиц, или нежесткими, состоящими из несвязанных твердых частиц.

Гибкие металлические перегородки используются для работы с агрессивными жидкостями, при повышенной температуре и значительных механических напряжениях. Они изготавливаются в виде перфорированных листов, сеток и тканей из стали, алюминия, никеля, серебра и различных сплавов.

Гибкие неметаллические перегородки изготавливаются в виде тканей или слоев несвязанных волокон (нетканые перегородки), реже – в форме перфорированных листов. Используют асбестовые, стеклянные, хлопчатобумажные и шерстяные ткани, а также ткани из синтетических волокон.

Негибкие жесткие перегородки выполняют в виде дисков, плиток, патронов. Они состоят из частиц твердого материала (металлические, керамические, стеклянные, угольные порошки, а также диатомит), жестко связанных между собой путем непосредственного спекания или спекания в присутствии связующего вещества так, что эти частицы образуют поры, проницаемые для жидкости.

Негибкие и нежесткие перегородки состоят из соприкасающихся жестко несвязанных твердых частиц, например каменного, древесного и животного углей, песка, некоторых неорганических солей.

Классификация фильтров. Фильтры классифицируются на фильтры периодического и непрерывного действия. На первых осуществляют любой режим фильтрования, на вторых практически — лишь режим фильтрования при постоянной разности давлений. Для проведения процессов фильтрования с закупориванием пор используют фильтры периодического действия.

По способу создания разности давлений фильтровальное оборудование может быть подразделено на фильтры, работающие под вакуумом, под давлением, и комбинированные фильтры.

По взаимному направлению силы тяжести и движения фильтрата фильтры могут быть с противоположными, совпадающими и перпендикулярными направлениями силы тяжести и движения фильтрата.

Фильтр-пресс с вертикальными рамами (плиточно-рамный фильтр-пресс), является фильтром периодического действия, работающим под давлением, в нем направления силы тяжести и движения фильтрата перпендикулярны. Фильтр-пресс состоит из станины 1, на которой смонтированы задняя упорная плита 5, передняя нажимная плита 9 и плиты 6, 8, установленные на два горизонтальных стержня 7.

Насос 2, нагнетающий суспензию в канал 4, приводится в движение электродвигателем 3. Нажимная плита 9 перемещается винтом 10 при помощи маховика 11. Уплотнение плит 8 производится винтом 10 с помощью рычага 12 или механическим приводом.

Собранные в пакет плиты с размещенными между ними фильтрующими пластинами плотно сжимаются. При этом фильтрующие пластины делят зазор между двумя плитами на две части, что достигается благодаря ребристой поверхности плит. Поэтому различают четные и нечетные отсеки. Если исходная суспензия поступает в четный отсек, осветленный сок будет выходить из нечетного отсека.

Каждая плита имеет по два фасонных прилива с отверстиями. Эти приливы расположены в двух углах четных плит с одной стороны, в нечетных плитах – с противоположной стороны. Таким образом, при сборе плит в пакет создаются два канала в четных и два канала в нечетных плитах, соединенных с полостями, образуемыми каждой парой плит с разделяющей их фильтрующей пластиной.

При работе фильтра фильтруемая суспензия нагнетается в каналы четных плит, затем через отверстия в них поступает в отсеки для исходной суспензии и под давлением проходит через фильтрующие пластины (рис. 2), при этом частицы взвесей задерживаются, а осветленная жидкость попадает в отсеки, затем по двум каналам нечетных пластин выходит из фильтра.

Фильтр-пресс используется в промышленности для разделения суспензий с небольшой концентрацией твердых частиц, когда трудоемкие операции разборки, разгрузки и сборки производятся относительно редко.

К достоинствам фильтр-прессов относится большая поверхность фильтрования на единицу занимаемой ими площади помещения и отсутствие движущихся частей в процессе эксплуатации. К недостаткам относится необходимость в ручном обслуживании, несовершенная промывка осадка и быстрое изнашивание фильтровальной ткани.

Интенсификация работы фильтров. Повысить производительность фильтров можно за счет увеличения поверхности и скорости фильтрования.

Оптимизации процесса фильтрования можно добиться тремя способами:

— конструкционным – реализуется при реверсивном (при малой толщине осадка), динамическом (при непрерывном смывании осадка), неодномерном (при образовании осадка на цилиндрической поверхности с малым радиусом кривизны) и вибрационном фильтровании;

— технологическим – направлен на выбор оптимальной толщины осадка, разности давлений, концентрации суспензии;

— физико-химическим – сводится к таким воздействиям на суспензию, которые обусловливают значительное уменьшение удельного сопротивления осадка. Этого можно добиться путем выбора надлежащих условий образования суспензии (температура, концентрация и др.), что позволит увеличить размер твердых частиц, получить кристаллические частицы вместо аморфных.

Расчет фильтров. Производительность фильтр-пресса зависит от скорости фильтрации, которая определяется режимом фильтрации, характером фильтрующей перегородки и физико-химическими свойствами осадка.

Производительность П (м 3 /с) фильтров и фильтр-прессов

, (10)

где q – нагрузка на фильтрующую поверхность, м 3 /м 2 ; F – площадь фильтрующей поверхности, м 2 ; t_пр, t_ф, t_р – соответственно продолжительность фильтрации, промывки осадка, разгрузки и подготовки фильтр-пресса к следующему циклу, с.

При выборе насоса, подающего исходный продукт в фильтр-пресс, необходимо учитывать сопротивление перегородки, которая рассчитывается по формуле

, (11)

где R₀ – коэффициент сопротивления; m – динамическая вязкость фильтрующего продукта, Па×с.

Продолжительность фильтрации t_ф (с)

, (12)

где М_ф – масса отфильтрованного сока за один цикл работы фильтр-пресса, кг; М_ос – масса влажного осадка, образующегося за один цикл работы фильтр-пресса, кг; d – толщина фильтрующей рамы, м; r_ос, r_с – соответственно плотность отфильтрованного сока и влажного осадка, кг/м 3 ; v_о – объемная скорость фильтрации сока, м 3 /(м 2 ×с).