Уравнение средней арифметической скорости молекул (6 видео)

Средняя скорость молекул

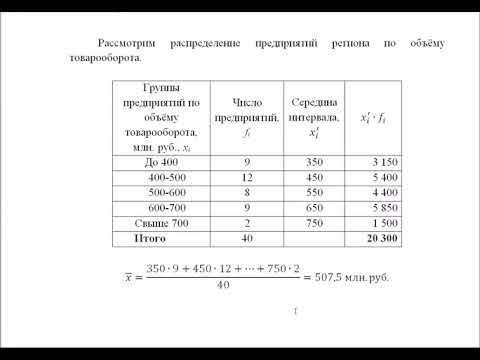
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.

Содержание

Средняя скорость движения молекул
Средняя квадратичная скорость
3.3. Характерные скорости молекул
Идеальный газ. Средняя квадратичная скорость
🔥 Видео

Видео:Измерение скоростей молекул газа | Физика 10 класс #32 | ИнфоурокСкачать

Средняя скорость движения молекул

Средняя скорость движения молекул называется также скоростью теплового движения молекул.

Формула средней относительной скорости молекул в физике представлена следующим выражением:

» open=» υ o t n = 2 8 k T πm 0 = 2 » open=» υ .

Видео:Урок 152. Среднеквадратичная скорость молекул. Опыт ШтернаСкачать

Средняя квадратичная скорость

Средняя квадратичная скорость движения молекул газа это следующая величина:

» open=» υ k υ = 1 N ∑ i = 1 N υ i 2

Формулу средней квадратичной скорости можно переписать так:

» open=» υ k υ 2 = ∫ 0 ∞ υ 2 F υ d υ .

Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:

» open=» υ k υ = 3 k T m 0 = 3 R T μ

Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:

p = 1 3 n m 0 » open=» υ k υ ,

где n = N V – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.

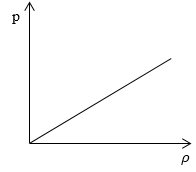
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1 ).

Запишем выражение для средней скорости движения молекул газа следующим образом:

» open=» υ = 8 k T πm 0

Из графика видно, что p

ρ или p = C ρ , где C – это некоторая константа.

m 0 = ρ n , p = n k T = C ρ → k T = C ρ n

Подставив m 0 = ρ n , p = n k T = C ρ → k T = C ρ n в » open=» υ = 8 k T πm 0 , получаем:

» open=» υ = 8 k T πm 0 = 8 C ρ π n n ρ = 8 C π

Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.

Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа ( p ) , молярная масса газа ( μ ) , а также концентрация молекул газа ( n ) ?

Применим выражение для » open=» υ k υ :

» open=» υ k υ = 3 R T μ

Помимо этого, из уравнения Менделеева-Клайперона и зная, что m μ = N N A :

p V = m μ R T = N N A R T .

Поделим правую и левую части p V = m μ R T = N N A R T на V , и зная N V = n , получаем:

p = n N A R T → R T = p N A n

Подставляем p = n N A R T → R T = p N A n в выражение для среднеквадратичной скорости » open=» υ k υ = 3 R T μ , получаем:

» open=» υ k υ = 3 p N A μ n

Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы » open=» υ k υ = 3 p N A μ n .

Видео:Урок 153. Распределение молекул по скоростямСкачать

3.3. Характерные скорости молекул

В этом разделе приводятся некоторые следствия, вытекающие из формул ( 3.29 ) и ( 3.30 ). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O₂ по абсолютным величинам скоростей при температурах Т₁ = 300 К и Т₂ = 1 300 К.

Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T₁ = 300 К и T₂ = 1 300 К

Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю

то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.

Наиболее вероятная скорость v_ВЕР — это скорость, отвечающая максимальному значению функции распределения.

Ее можно найти, решая уравнение

откуда следует, что

Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:

Соотношения (3.31), (3.32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода при температуре и для гелия при температуре .

С ростом температуры наиболее вероятная скорость v_ВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т₂ > Т₁. При этом f(v_ВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения f(v) площадь под кривыми постоянна и равна единице в соответствии с формулой ( 3.30 ).

Относительное количество молекул, скорость которых превышает некоторое значение v₀, определяется выражением

На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v₀ часть площади (отмечена штриховкой), ограниченная кривой f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v₀, растет с повышением температуры.

В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана

Умножая числитель и знаменатель на число Авогадро N_A и учитывая, что

— молярная масса газа, a

— универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме

Распределение молекул по величинам безразмерной скорости. Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул v, то форма кривой и положение максимума будут зависеть от массы молекул и от температуры газа. Но если по горизонтальной оси откладывать отношение скорости к наиболее вероятной скорости, то есть безразмерную скорость

то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).

Рис. 3.4. Распределение Максвелла по величинам безразмерной скорости

Сделав замену переменной

в ( 3.29 ) и учитывая, что

получим распределение Максвелла в форме

Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.

Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562–572 м/с.

Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = v_ВЕР. Величина интервала du = 0,02. Следовательно,

Вычислим наиболее вероятную скорость:

Найдем отношение v = 562 м/с к v_ВЕР = 395 м/с

Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = 0,62. Ширина интервала Dv = 10 м/с (Du = 10/395 = 0,0253). Следовательно, доля молекул в этом интервале

Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.

Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости v 2 или кинетической энергии молекулы mv 2 /2.

Средняя арифметическая скорость — это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул.

Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dv_i. Каждому интервалу соответствует количество молекул

Так как интервалы Dv_i, малы, то можно приближенно считать скорости молекул данного интервала одинаковыми и равными v_i. Сумма значений скоростей молекул интервала

Сумма значений скоростей всех молекул

Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости

Переходя от суммы к интегралу, получаем

Вычисляя интеграл, получаем среднюю арифметическую скорость молекул

Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям скорости:

В частности, при L(v) = v отсюда находится .

Среднее значение квадрата скорости равно отношению суммы квадратов скоростей всех молекул системы к общему числу молекул. Таким образом,

Среднеквадратичная скорость — это корень квадратный из среднего значения квадрата скорости молекул

Следует отметить, что характерные скорости отличаются друг от друга лишь численными множителями, причем

а зависимость от Т и m₀ (или m) у них одинаковая.

Через среднеквадратичную скорость выражается средняя кинетическая энергия поступательного движения молекул

Этот результат находится в согласии с формулой (1.14) кинетической теории идеальных газов и с законом о равнораспределении энергии, который гласит, что на каждую степень свободы молекулы приходится энергия k_BТ/2. Три степени свободы поступательного движения молекулы как раз соответствуют полученному здесь результату (3.44). В сущности, именно для того, чтобы получить такое соответствие, мы выбрали должным образом коэффициент α в ( 3.26 ).

Эксперимент по проверке распределения Максвелла. Необходимо еще раз подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия справедливы только для газа, находящегося в равновесии.

Закон справедлив для любого числа молекул N, если только это число достаточно велико. Закон Максвелла — статистический, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказанной статистики — флуктуации.

Экспериментальное определение распределения скоростей молекул было осуществлено впервые О. Штерном в 1920 г. Исследовалось распределение по скоростям одноатомных молекул паров металлов (Ag или Pt), из которых была изготовлена нить, расположенная на оси двух цилиндров. Нить нагревалась электрическим током, и металл испарялся (см. рис 3.5).

Рис. 3.5 Схема опыта Штерна: 1 — вид установки сбоку; 2 — вид установки сверху

Молекулы, прошедшие через щель во внутреннем цилиндре, летели по прямой и оседали на стенке холодного внешнего цилиндра. Если привести всю установку во вращение (щель все время против точки В₀), то молекулы, обладающие большой скоростью v, попадут в некоторую точку вблизи В₀, а более медленные затратят на путь больше времени и попадут в точки, отстоящие дальше от В₀. Следует обратить внимание, что вылетающие молекулы движутся по прямой, они не участвуют во вращательном движении. Поскольку молекулы в зависимости от скорости попадают в разные точки внешнего цилиндра, то исследуя толщину слоя металла, осевшего на его стенку, можно составить представление о распределении молекул по скоростям.

Найдем распределение молекул по расстояниям S от точки В₀ до места их попадания на стенку цилиндра. Если R и r — радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра

За это время цилиндр повернется на угол

где ω — угловая скорость вращения установки. Соответственно, точка попадания будет смещена относительно В₀ на расстояние

Подставляя сюда время полета, получаем связь скорости молекулы с расстоянием S:

Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что

находим распределение молекул по расстояниям S:

(мы опускаем выражение для нормировочной постоянной С).

Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.

Видео:Распределение Максвелла — Больцмана (часть 6) | Термодинамика | ФизикаСкачать

Идеальный газ. Средняя квадратичная скорость

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы введём понятие идеального газа, то есть газа, в котором молекулы не взаимодействуют между собой и не обладают объёмом. Также мы узнаем, что такое средняя квадратичная скорость молекул, микро- и макропараметры, и рассмотрим применение модели идеального газа.