Уравнение спрямляющей плоскости к кривой (4 видео)

VMath

Содержание

Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Касательная к кривой
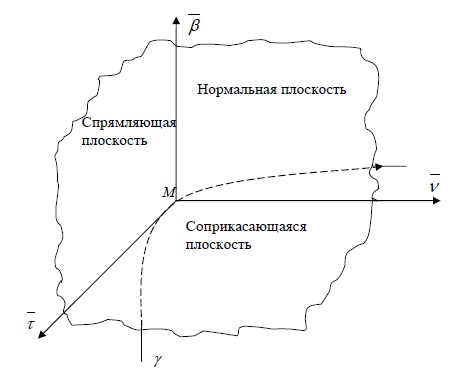
Нормальная плоскость
Соприкасающаяся плоскость
Бинормаль и главная нормаль
Спрямляющая плоскость
Репер Френе
Решение задач
Задача 1
Решение задачи 1
Задача 2
Решение задачи 2
Задача 3
Решение задачи 3
Уравнение спрямляющей плоскости к кривой
Глава 1 Элементы дифференциальной геометрии (стр. 1 )
Тогда с учетом формул (1.9), (1.12), имеем
📸 Видео

Инструменты сайта

Основное

Информация

Действия

Содержание

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Дифференциальная геометрия | плоская кривая и её параметризацияСкачать

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.

Видео:Дифференциальная геометрия | спрямляющая плоскостьСкачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Уравнение спрямляющей плоскости к кривой

Пространственные кривые. Задание пространственной кривой. Регулярное задание кривой. Регулярная кривая. Неявное задание пространственной кривой. Касательная к пространственной кривой. Единичный вектор касательной. Бинормаль и главная нормаль и их единичные векторы. Нормальная, соприкасающаяся и спрямляющая плоскости. Ускорение при криволинейном движении и векторы сопровождающего трехгранника. Кривизна пространственной кривой. Теорема о прямой. Кручение пространственной кривой. Теорема о плоской кривой. Формулы Френе. Естественный параметр и натуральные уравнения кривой.

Основные определения, результаты, комментарии

Элементарной кривой в пространстве называется образ открытого интервала при его гомеоморфизме в евклидово трехмерное пространство.

Общей кривой на плоскости называется подмножество евклидова пространства, локально гомеоморфное прямой.

Как и в случае плоских кривых, всякая общая кривая допускает покрытие элементарными кривыми.

Кривая задана неявным способом

если координаты каждой точки кривой удовлетворяют обоим уравнениям .

Наиболее удобны и наиболее часто используются векторно-параметрическое представление

и координатно-параметрическое представление

отличающиеся лишь формой записи.

Определение регулярности параметрического представления пространственной кривой полностью аналогично плоскому случаю.

Неявное задание (5) кривой регулярно в точке , если матрица частных производных

имеет в этой точке ранг 2.

Понятия длины кривой, ее естественной параметризации, а также определение касательной полностью аналогичны тем же понятиям для плоских кривых. Направляющий вектор касательной — это, по-прежнему, производная , имеющая физический смысл скорости, если параметрическое представление кривой интерпретировать как кинематическое описание движения точки.

Нормальная плоскость кривой в точке — это плоскость, проходящая через точку ортогонально касательной.

Соприкасающейся плоскостью кривой в ее точке (рис. 17) называется содержащая эту точку плоскость , удовлетворяющая соотношению

где — точка, принадлежащая элементарной окрестности точки .

Спрямляющей плоскостью кривой в ее точке называется содержащая эту точку плоскость, ортогональная нормальной и соприкасающейся плоскостям в этой точке.

Прямые, ортогональные соприкасающейся и спрямляющей плоскостям в точке , называются соответственно бинормалью и главной нормалью кривой в точке .

Нормальная, соприкасающаяся и спрямляющая плоскости образуют сопровождающий трехгранник кривой , или трехгранник Френе , в точке , и называются его гранями . Касательная, бинормаль и главная нормаль называются ребрами сопровождающего трехгранника (рис. 18).

Уравнения элементов сопровождающего трехгранника вычисляются по следующим правилам:

Касательная	Нормальная плоскость
Бинормаль	Соприкасающаяся плоскость
Главная нормаль	Спрямляющая плоскость

Единичные векторы

касательной

главной нормали

бинормали

Если параметризация естественная , то вектор главной нормали может быть вычислен по формуле .

Вектор ускорения может быть разложен в сумму двух составляющих: нормальной (ортогональной вектору скорости) и тангенциальной (параллельной вектору скорости). При этом нормальная составляющая ускорения сонаправлена единичному вектору главной нормали.

Пусть и — две различные точки кривой , соответствующие значениям и естественного параметра. Тогда — длина дуги кривой, заключенной между точками и . Пусть — величина угла, образуемого касательной к кривой в точке по отношению к касательной в точке . Кривизна кривой в ее точке — это предел

В отличие от кривизны плоской кривой, кривизна пространственной кривой всегда положительна . Кривизна пространственной кривой в регулярной точке может быть вычислена по формулам:

если параметризация естественная.

Пусть и — две различные точки кривой , соответствующие значениям естественного параметра и соответственно, и — единичные векторы бинормалей в этих точках (рис. 19).

Обозначим за величину угла между ними. Очевидно, этот угол равен углу, образованному соприкасающимися плоскостями в точках и .

Абсолютным кручением кривой в точке называют величину

Кручение кривой определяется в соответствии со следующим правилом: если при движении вдоль кривой по направлению возрастания параметра вектор бинормали поворачивается в сторону, указываемую вектором , в противном случае. Наглядно это означает, что кривая с положительным кручением «закручена» по правилу правого винта.

Кручение кривой в точке, соответствующей значению параметра , может быть вычислено по следующим формулам:

Для производных векторов , по естественному параметру справедливы формулы Френе :

Уравнения и называются натуральными уравнениями кривой. По натуральным уравнениям вид кривой может быть восстановлен с точностью до перемещения. В большинстве случаев решение такой задачи оказывается очень сложным.

1. Для данных представлений кривых укажите область допустимых значений параметра и область значений параметра, в которой задание кривой регулярно.
1)
2)
3)
4) .

2. Кривая задана неявными уравнениями. Изобразите на рисунке вид кривой. Постройте какое-нибудь параметрическое представления этой кривой. Укажите область допустимого изменения параметра и область регулярности параметризации.
1)
2) R,;; y>0;$ —> R,;; y>0;$»>
3)

3. Кривая Вивиани образована пересечением сферы радиуса и цилиндра радиуса , проходящего через центр сферы. Постройте параметрическое представление кривой Вивиани.

4. Винтовая линия. Окружность радиуса движется так, что ее центр перемещается вдоль оси , плоскость ортогональна оси . По окружности равномерно движется точка. В начальный момент времени точка имеет координаты . Составьте параметрические уравнения кривой, описываемой данной точкой.

5. Кривая задана пересечением цилиндрических поверхностей и Постройте параметрическое представление кривой , не содержащее радикалов, и дайте ее изображение.

6. Покажите, что линия

принадлежит сфере и является линией пересечения параболического и кругового цилиндров.

7. Найдите длину дуги линии

между плоскостями и .

8. Покажите, что кривая замкнута и имеет длину .

9. Запишите в естественной параметризации
a) винтовую линию ;
б) гиперболическую винтовую линию .

10. Кривая задана параметрически: 0. end —>

Напишите уравнения
а) касательной и нормальной плоскости в точке (1/4; 1/3; 1/2);
б) касательной, параллельной плоскости .

11. Найдите линию, по которой касательные к линии

Сферической индикатрисой данной кривой называется геометрическое место концов единичных касательных векторов, отложенных от начала координат.

12. Дана винтовая линия

a) Напишите уравнение семейства касательных этой кривой;
б) убедитесь в том, что все касательные к винтовой линии образуют с плоскостью один и тот же угол;
в) составьте уравнение кривой, образуемой точками пересечения касательных с плоскостью ;
г) найдите сферическую индикатрису винтовой линии.

13. Докажите, что все нормальные плоскости кривой Вивиани (задача 3) проходят через начало координат.

14. Составьте уравнения бинормали и главной нормали кривой в указанной точке:
1)
2)
3) ;
4)

15. Найдите точки на кривой

в которых бинормаль параллельна плоскости .

16. Материальная точка движется в пространстве по закону

Укажите моменты времени, в которые
а) ее скорость равна нулю, и сравните их со значениями параметра , при которых параметризация траектории нерегулярна;
б) нормальное ускорение точки ортогонально .

17. Составьте уравнения ребер и граней сопровождающего трехгранника данной кривой в указанной точке
1)
2)
3)
4)

18. Для данной кривой вычислите кривизну в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных касательных векторов данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.
1) 0,;; bne 0, ;; t_0=pi/2$ —> 0,;; bne 0, ;; t_0=pi/2$»>
2)

19. Для кривых задачи 18 вычислите абсолютное кручение в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных векторов бинормали данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.

20. Вычислите кривизну и кручение данной кривой произвольной регулярной точке:
1) 0,;; bne 0$ —> 0,;; bne 0$»>;
2)
3)
4) .

21. Найдите точки распрямления следующих кривых:
1)
2)
3) .

22. Найдите точки уплощения и дуги, на которых кручение сохраняет свой знак, у следующих кривых:
1)
2)

23. Напишите натуральные уравнения, которым удовлетворяют следующие кривые:
1) 0,;; bne 0$ —> 0,;; bne 0$»>;
2)

24. Найдите точки на кривой

в которых кривизна принимает локально минимальное значение.

25. Найдите точки на кривой

в которых радиус кривизны достигает локального максимума.

26. Докажите, что следующие кривые плоские, и составьте уравнения плоскостей, в которых они расположены:

27. Найдите такую функцию , чтобы кривая

была плоской. Решите задачу двумя способами: 1) используя условие плоскости и 2) используя тот факт, что искомая кривая принадлежит круговому цилиндру (составьте его уравнение!). Результаты сравните.

28. Докажите, что если все соприкасающиеся плоскости линии проходят через неподвижную точку , то линия плоская.

29. Докажите, что если соприкасающиеся плоскости линии (отличной от прямой) параллельны некоторому вектору , то линия плоская.

30. Докажите, что если все нормальные плоскости линии параллельны некоторому вектору , то линия или прямая, или плоская.

Видео:Дифференциальная геометрия | кривизна плоской кривойСкачать

Глава 1 Элементы дифференциальной геометрии (стр. 1 )

Уравнение спрямляющей плоскости к кривой

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7

Дифференциальная геометрия изучает геометрические свойства пространственных и плоских кривых линий и поверхностей. В данной работе рассматриваются наиболее общие свойства геометрических объектов, необходимые для конструирования и расчета напряженно деформированного состояния оболочек. Для более углубленного изучения геометрии поверхностей можно использовать многочисленную специальную литературу.

1.1. Элементы теории кривых

Кривой линией называется множество точек, состоящее из конечного или счетного множества простых дуг, примыкающих друг к другу. Уравнение кривой может быть задано в векторном или параметрическом виде

, (1.1)

где r(t) – радиус вектор кривой; t – параметр, задающий положение точки пространственной кривой; X(t), Y(t), Z(t) – координаты произвольной точки линии в прямоугольной декартовой системе координат; i, j, k – орты прямоугольной системы координат (рис. 1.1).

Производная радиуса вектор кривой r(t) по параметру t определяет вектор касательной к кривой линии в заданной точке

. (1.2)

Модуль производной радиус-вектора кривой линии определяет длину дуги кривой линии:

; (1.3)

; . (1.4)

Так как между длиной дуги s и параметром t, формулой (1.4) определяется однозначное соответствие, то длина кривой может рассматриваться как параметр, определяющий положение точки кривой (t0 принимается за начальную точку отсчета длины кривой линии)

. (1.5)

Параметр s оказывается наиболее удобным при изучении свойств кривой линии по ее уравнению и называется натуральным параметром, а уравнение (1.5) – натуральным уравнением кривой.

Дифференцируя радиус-вектор кривой по параметру t и учитывая зависимость s = s(t), имеем

. (1.6)

Из соотношения (1.6) следует, что |dr/ds| = 1 и, следовательно,

, (1.7)

где τ – единичный вектор касательной кривой линии в заданной точке (рис. 1.1). В дальнейшем единичный вектор касательной будем называть просто вектор касательной кривой линии.

Прежде чем продолжить изучение свойств кривой линии, рассмотрим вектор постоянный длины R(t) (|R(t)| = a = const), т. е. вектор, меняющий только направление при изменение параметра t. Если при этом, один конец вектора расположен в заданной точке, то очевидно второй конец вектора описывает кривую на сфере радиуса, равного длине вектора, и вектор касательной расположен в касательной плоскости сферы и перпендикулярен вектору R(t). Докажем аналитически свойство перпендикулярности вектора производной вектору-функции постоянной длины

;

Дифференцируя квадрат вектора постоянной длины, получим

. (1.8)

Но равенство нулю скалярного произведения двух векторов (каждый из которых не равен нулю) означает их ортогональность, следовательно, вектор производной вектор-функции постоянной длины перпендикулярен этой вектор-функции.

Вернемся к изучению свойств кривой линии.

Плоскость перпендикулярная вектору касательной кривой называется нормальной плоскостью кривой в данной точке.

Плоскость, содержащая вектор касательной кривой называется касательной плоскостью кривой в данной точке. Очевидно, через точку кривой линии можно провести бесконечное число касательных плоскостей.

Так как касательный вектор τ кривой линии является вектором единичной длины, то вектор его производной ортогонален вектору касательной, т. е. лежит в нормальной плоскости кривой.

В точке кривой можно провести бесконечное множество нормалей, которые лежат в нормальной плоскости кривой. Нормаль кривой, совпадающая с направлением вектора производной касательного вектора, называется главной нормалью кривой линии.

Касательная плоскость, проходящая через главную нормаль кривой, называется соприкасающейся плоскостью. В частности, для плоской кривой соприкасающаяся плоскость является плоскостью, в которой лежит плоская кривая. Соприкасающуюся плоскость можно также получить, как предельное положение плоскости, проходящей через три неограниченно сближающиеся точки кривой линии.

Дифференцируя дважды радиус-вектор кривой по натуральному параметру, получим вектор главной нормали кривой линии в заданной точке

, (1.9)

где v – единичный вектор нормали кривой;

– кривизна кривой линии.

Вектор, перпендикулярный соприкасающейся плоскости, т. е. перпендикулярный векторам касательной и главной нормали называется бинормалью кривой линии. Очевидно, единичный вектор бинормали кривой можно определить как векторное произведение векторов касательной и нормали

. (1.10)

Касательная плоскость, проходящая через бинормаль, называется спрямляющей плоскостью кривой линии.

Касательная, нормаль и бинормаль определяют в каждой точке кривой три единичных взаимно перпендикулярных вектора (риc. 1.1), которые называют натуральным трехгранником кривой, или трехгранником Френе.

Основные свойства векторов трехгранника Френе:

; ;

; ; ;

; ; . (1.11)

Дифференцируя соотношение (1.10) по натуральному параметру, получим вектор, лежащий в соприкасающейся плоскости:

, (1.12)

где χ = |dβ/ds| – кручение кривой линии.

Дифференцируя скалярное произведение двух любых взаимно перпендикулярных векторов (e1·e2) = 0, имеем

, или .

Дифференцируя скалярные произведения векторов трехгранника Френе (1.11), получим

; ; .

Видео:Дифференциальная геометрияСкачать

Тогда с учетом формул (1.9), (1.12), имеем

. (1.13)

Формулы дифференцирования векторов трехгранника Френе (1.9), (1.12), (1.13)

; ; (1.14)

называются формулами Серре-Френе.

Геометрический смысл кривизны и кручения кривой линии можно получить рассматривая перемещение трехгранника Френе вдоль кривой линии. При перемещении вдоль кривой на расстояние Ds направление касательной изменяется. Касательная поворачивается на некоторый угол Δφ (рис. 1.2). Скорость изменения угла направления касательной, определяемая пределом отношения угла поворота касательной к длине дуги кривой называется кривизной кривой линии:

. (1.15)

Сравнивая определение кривизны (1.15) с формулой дифференцирования вектора касательной, имеем

так как для вектора единичной длины

Из рис 1.2 ясно, что приращение касательной Δτ и, следовательно, нормаль ν, при движении вдоль кривой линии всегда направлены в сторону вогнутости кривой.