Функция Стоуна U(x, y)=(x-a)α(y-b)β
Здесь 



1. Нахождение функций спроса по Маршаллу:
Исследуем задачу рационального потребительского выбора, если предпочтения потребителя описываются функцией Стоуна.

Составляем условия первого порядка (затем делим первое уравнение на второе):
В полученной системе верхнее уравнение – расписанное для функции Стоуна правило: соотношение предельных полезностей равно соотношению цен на продукты. Нижнее уравнение – ограничение в оптимизационной задаче.
Два уравнения – два неизвестных (x и y). Решаем систему и получаем однозначное решение – функции спроса по Маршалу.
2. Рассчитаем функцию косвенной полезности:
Подставим в функцию полезности вместо x и y полученные функции Маршала:
3. Кривые Энгеля
Алгебраический вид кривых получается из функций Маршала подстановкой в них конкретных значений всех параметров и переменных кроме x, y, M. Геометрический вид:
Кривые расходов Энгеля
Минимальные Дополнительные расходы
расходы на на товар x при наличии
товар x суммы денег превышающей
предпочтений потребителя 45º
(доля расходов на товар х
из «дополнительных» денег)
Минимальные Дополнительные расходы
расходы на на товар y при наличии
товар y суммы денег превышающей
предпочтений потребителя 45º
(доля расходов на товар y
из «дополнительных» денег)
По виду кривых расходов Энгеля можно сделать вывод о нормальльности исследуемых товаров.
4. Кривая «доход-потребление»
Алгебраически выводится из функций Маршала. Рассматриваются два уравнения (функции Маршала для товаров x и y) с тремя неизвестными: x, y, M. Исключая M – получаем одно уравнение – множество оптимальных пар (x, y) при различных уровнях дохода М индивида. Получаем уравнение оптимальных точек аналогичное полученному при построении условий первого порядка:

Наклон
5. Кривая «цена товара х – потребление»
6. Кривая «цена товара y – потребление»
Алгебраически строятся аналогично кривой «доход-потребление», только третьим неизвестным фактором выступает не доход (М) а соответствующая цена. Получается абсолютно такая же зависимость координат оптимальных точек, такие же графики.
7. Функции спроса по Хиксу.
Составим оптимизационную задачу (минимум расходов на достижение заданного уровня полезности)
Составим функцию Лагранжа:
Найдем условия первого порядка:
Получим функции спроса Хикса
8. Функция расходов
Подставим полученные функции спроса (по Хиксу) вместо количества товаров x и y в уравнение бюджетного ограничения – получим зависимость расходов от цен товаров и уровня желаемой полезности набора – это функция расходов.
 |  |
Минимально «дополнительные» расходы,
необходимые связанные с желаемым уровнем полезности,
автономные ценами товаров, предпочтениями потребителя
ОБЩИЙ ЭФФЕКТ показывает как изменился объем потребления товара при изменении его цены. Если зависимость между изменением цены и объемом потребления данного товара прямая, то есть закон спроса нарушен, то такие блага называют товарами Гиффена.
по Хиксу показывает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.
по Слуцкому показывает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителю возможности приобрести первоначальный набор продуктов.
Эффект замены всегда отрицателен. Под этим утверждением понимается, что зависимость между ценой товара и объемом потребления при эффекте замены всегда обратная. То есть, при снижении цены объем потребления товара в ходе эффекта замены всегда будет расти (не убывать), а при увеличении цены – наоборот, снижаться (не возрастать). Таким образом, направление эффекта замены – движение из первоначальной точки оптимума потребителя вдоль первоначальной кривой безразличия в промежуточную (вспомогательную, построенную нами для расчета эффектов) точку.
ЭФФЕКТ ДОХОДА показывает на сколько изменится объем потребления данного блага за счет того, что потребитель начинает чувствовать себя богаче (рост реального дохода потребителя при снижении цены на товар) или беднее (снижение реального дохода при росте цены). Эффект дохода может быть как положительным, так и отрицательным.
По Хиксу – рост изменение дохода на столько, чтобы при новых ценах попасть на старую кривую безразличия.
По Слуцкому – рост изменения дохода на столько, чтобы при новых ценах можно было бы купить старый набор товаров.
ПОЛОЖИТЕЛЬНЫЙ ЭФФЕКТ ДОХОДА: прямая зависимость между изменением реального дохода и объемом потребления товара
а) при снижении цены товара, что эквивалентно росту реального дохода потребителя, объем потребления данного товара тоже вырастет (Pa↓, Iреальный ↑, Qa↑);
б) при росте цены товара, что эквивалентно снижению реального дохода потребителя, объем потребления данного товара (за счет эффекта дохода) сократится (Pa↑, то есть I реальный ↓ и Qa ↓)
При положительном эффекте дохода мы делаем вывод о том, что данный товар является качественным.
ОТРИЦАТЕЛЬНЫЙ ЭФФЕКТ ДОХОДА: обратная зависимость между изменением реального дохода и объемом потребления товара
а) при снижении цены товара, что эквивалентно росту реального дохода потребителя, объем потребления данного товара снизился (Pa ↓, то есть Iреальный ↑, Qa ↓);
б) при росте цены товара, что эквивалентно снижению реального дохода потребителя, объем потребления данного товара (за счет эффекта дохода) вырастет (Pa↑, то есть I реальный ↓, Qa ↑)
При отрицательном эффекте дохода мы делаем вывод о том, что данный товар является некачественным для потребителя.
Направление эффекта дохода – движение из промежуточной (вспомогательной, построенной нами для расчета эффектов) точки, в которую мы как бы перешли из первоначальной за счет эффекта замены, в конечную, расположенную на новой (конечной) кривой безразличия.
Рассмотрим случай, когда понижается цена товара Y. Эффекты по Хиксу.
Эффекты по Слуцкому
Общая ситуация: возможно построение всех видов индексов количества и цен, номинального дохода, Пааше и Ласпейреса, простых и теоретических. В общем случае нет совпадений.
При их построении ориентируются на определение Слуцкого неизменного благосостояния индивида: если индивид может приобрести в различных экономических условиях один и тот же набор товаров, то его благосостояние в этих различных условиях одинаково.
Алгебраические формулы индексов:
Индекс цен Ласпейреса 
Индекс реального 
дохода Ласпейреса дохода Пааше
Индекс реального дохода:
Очевидны тождества:
Рассмотрим ситуацию, когда понижается цена товара Y.
При их построении ориентируются на определение Хикса неизменного благосостояния индивида: если индивид получает один тот же уровень полезности от двух наборов товаров, то его благосостояние при потреблении этих наборов одинаково.
Цены первоначальные pA, цены конечные – pB;
набор товаров первоначальный (xA, yA), конечный –(xB, yB), наборы «вспомогательные» — соответствующие оптимуму при компенсационном изменении дохода – (xC, yC), при эквивалентном – (xD, yD).
Алгебраические формулы индексов:
Индекс цен Ласпейреса 
Индекс реального 
дохода Ласпейреса дохода Пааше
Индекс реального дохода:
Очевидны тождества:
Рассмотрим ситуацию, когда понижается цена товара Y.
a
ДАНО: Функция полезности потребителя задана уравнением U=X2Y. Общий доход, которым располагает потребитель, равен 240 у. е. Цена товара Х: Рх=4 у. е.; цена товара У: Ру=8 у. е. Если цена товара У снижается до Ру2=5 у. е., рассчитайте эффект замены, эффект дохода и общий эффект (по Хиксу). Охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
1. (Функции спроса Маршала)
Функция полезности потребителя представляет собой функцию Кобба-Дугласа (Функция вида 
Графическое представление оптимальной точки – это точка касания бюджетного ограничения потребителя и кривой безразличия. Исходя из этого, в точке оптимума угол наклона кривой безразличия (

Решая данную систему для функции вида Кобба-Дугласа (
Полученные формулы справедливы для любой функции Кобба-Дугласа и получили название «метода долей дохода».
2. Функция косвенной полезности:
3. Кривые Энгеля:
Кривые расходов Энгеля
4.
Кривая «доход-потребление» y


5. Кривая «цена товара Х – потребление»




Стрелками на графике показано направление перемещения оптимального набора при росте цены товара Х. Точка (0,10) выколота.
6. Кривая «цена товара Y – потребление»


 |


Стрелками на графике показано направление перемещения оптимального набора при росте цены товара Y. Точка (0,40) выколота.
7. Функции спроса по Хиксу:
Первоначальное состояние – точка A, (х, у) рассчитываются с помощью функций спроса Маршала.


Конечное состояние – точка В, (х, у) рассчитываются с помощью функций спроса Маршала.


Рассчитаем эффекты по Хиксу:
Переходное состояние – вспомогательная точка С, (x, y) рассчитываются с помощью функций спроса Хикса.
Следовательно, после снижения цены товара У, потребитель увеличил объем потребления этого товара на 6 единиц. Таким образом, общий эффект от снижения цены товара У равен +6 ед. (ΔYобщий=Yконечное – Yначальное = 16-10).
Эффект ЗАМЕНЫ: при снижении цены товара У, объем потребления товара У (при сохранении потребителем первоначального уровня полезности) увеличился на 3,7 ед. (ΔYзамены=Yпромежуточное – Yначальное =13,7-10).
Эффект ДОХОДА: при снижении цены товара У, что эквивалентно росту реального дохода потребителя, объем потребления товара У увеличился на 2,3 ед. (ΔYдохода=Yконечное – Yпромежуточное =16-13,7), то есть прямая зависимость между изменением реального дохода и объемом потребления, следовательно Y — товар нормальный.
Проверка: Общий Эффект = Эффект замены + Эффект дохода; то есть общее изменение объема потребления товара потребителем при изменении цены данного товара складывается из изменения объема за счет эффекта замены и изменения объема за счет эффекта дохода. Таким образом: +2,3 + 3,7= +6.
Выводы: товар У является нормальным (качественным товаром). Закон спроса (обратная зависимость между ценой товара и объемом потребления ) не нарушен (в данном случае, цена товара У снизилась, что в итоге привело к росту объема потребления данного товара на 6 единиц (то есть обратная зависимость).
Такие же рассчеты можно провести относительно товара Х:
Общий эффект=хВ-хА=40-40=0=эффект замены+эффект дохода
Рассчитаем эффекты по Слуцкому:
Вспомогательная точка С строится так:
— через точку А проводим линию бюджетного ограничения с новыми ценами
— проводим касательно к этому Б. О.(С) кривую безразличия, точка касания – точка С.
Такие же расчеты можно провести относительно товара Y:
Общий эффект = yВ-yА=16-10=6=эффект замены+эффект дохода
Эффект замены = yС-yА=14-10=4
Эффект дохода = yВ-yС=16-14=2
Такие же расчеты можно провести относительно товара Х:
Общий эффект=хВ-хА=40-40=0=эффект замены+эффект дохода
Обратим внимание, что для товаров Х и У, в этой задаче, эффект замены по Слуцкому больше, чем по Хиксу, а эффект дохода по Слуцкому меньше, чем по Хиксу.
дохода Ласпейреса дохода Пааше
Индекс реального дохода:
Очевидны тождества:
Рассчитаем координаты точки D с помощью функций спроса Хикса.
Индекс реального дохода: 
Очевидны тождества:
Видео:Равновесная цена | Крест МаршаллаСкачать

Уравнение спроса по маршаллу пример
Связь между кривыми спроса, построенными согласно двум интерпретациям, изображена на рис. 1. Кривая Cc представляет собой кривую спроса отдельного потребителя на товар X, построенную в соответствии с общепринятой интерпретацией. Предполагается, что денежный доход и цены прочих товаров одинаковы во всех ее точках; следовательно, реальный доход в точке С ниже, чем в точке Р, а отсюда, если бы индивидуум стремился купить ОМ товара X по цене OC, то он вынужден был бы сократить свои покупки каких-либо других товаров. Согласно изображенной кривой он, разумеется, не купит никакого количества товара X по цене OC, истратив сумму ОНРМ на другие товары, которые, как показывает его действие, при цене ОН оцениваются им менее высоко, чем ОМ товара X. Ордината представляет отношение цены товара X к цене других товаров. Для кривой спроса Cc это вопрос только единицы измерения, так как предполагается, что другие цены одинаковы во всех ее точках.
Видео:Как спрос и предложение задают ценыСкачать

Уравнение спроса по маршаллу пример
• Место Маршалла в истории экономической мысли
• Метод частичного равновесия
• Анализ полезности и спроса
• Анализ издержек и предложения
• Равновесная цена и влияние фактора времени
• Элементы теории благосостояния
Альфред Маршалл (1842-1924) — одна из наиболее выдающихся личностей в истории экономической мысли. По влиянию на развитие экономической теории XX в. его можно сравнить разве что с Вальрасом, а его «Принципы экономической науки» являются, пожалуй, единственной книгой по экономической теории XIX в., которую можно рекомендовать изучающим микроэкономику даже в конце XX в.
Вопреки желанию отца, который хотел видеть сына студентом Оксфордского университета, а затем священником, Маршалл получил математическое образование в Кембридже. Биографы неизменно отмечают тот факт, что он стал вторым из всех кембриджских бакалавров на открытом экзамене по математике (первым был будущий знаменитый математик лорд Рейли). Так или иначе, математическая подготовка Маршалла превосходила уровень всех его современников-маржиналистов. Тогда же в Кембридже проявились и чрезвычайно разносторонние интересы Маршалла в области философии и общественных наук. По его собственным воспоминаниям, он шел от метафизики к этике, от этики к политической экономии. Изучая труды Рикардо и Дж. Ст. Милля, Маршалл перекладывал их для себя на язык диаграмм, что в дальнейшем привело его к графическому методу анализа, закрепившемуся в современной экономической науке именно благодаря его усилиям. С 1877 по 1885 г. Маршалл преподавал политическую экономию сначала в Бристоле, а затем в Оксфорде. С 1885 до 1908 г. был профессором Кембриджского университета, где стал основоположником знаменитой Кембриджской школы. Среди его учеников были А.С. Пигу, Дж.М. Кейнс, Дж. Робинсон и многие другие. Слава Маршалла как ведущего экономиста-теоретика долгое время основывалась именно на его лекциях, поскольку, стремясь к совершенству, он мучительно долго (около 20 лет) писал и готовил к печати свой главный труд: «Принципы экономической науки» (1890) . Другие книги Маршалла: «Экономика промышленности» (1879; написана вместе с женой Мэри Пейли и содержит некоторые элементы, развитые позднее в «Принципах. »), «Промышленность и торговля» (1919) и «Деньги, кредит и коммерция» (1923) — содержат преимущественно более ранние работы Маршалла. Благодаря активной преподавательской деятельности и влиянию «Принципов. » Маршалл доминировал в британской экономической науке с 1890-х до начала 1930-х годов.
Маршалл был завершающей, систематизирующей фигурой маржиналистской революции в том же смысле, в каком Дж. Ст. Милль выполнял ту же функцию для классической школы. Как и труд Милля, «Принципы. » Маршалла являлись наиболее полным сводом существующей теории и учебником для многих поколений студентов.
🎬 Видео
Эластичность спроса и предложения | Как цена влияет на спросСкачать

Спрос и предложение разбор задачСкачать

2.1 Спрос и величина спросаСкачать
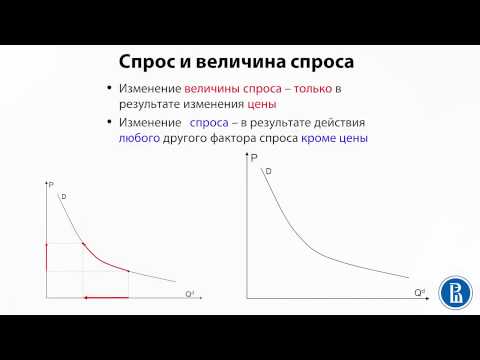
2.3 Рыночное равновесиеСкачать

9.6 Количественная теория денег Монетизация экономикиСкачать

Что такое спрос и предложение? Неценовые факторы спроса и предложения | обществознание ЕГЭ 2022Скачать

4.1.2. Паутинообразная модель рынкаСкачать

Микра для начинающих/ЭД и ЭЗ. Модель ХиксаСкачать

Микра для начинающих/ЭД и ЭЗ. Модель СлуцкогоСкачать
Экономика 10 класс (Урок№8 - Рыночное равновесие.)Скачать

Микра для начинающих/Эффект дохода и эффект замещенияСкачать
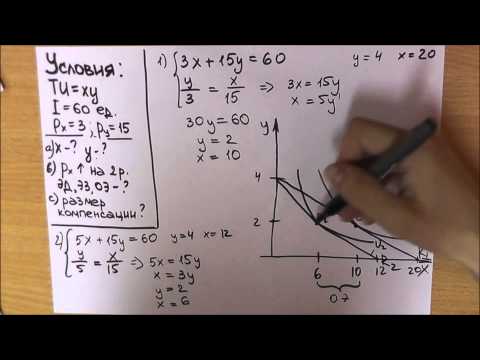
Изменение спросa и изменение величины спроса | МакроэкономикаСкачать

3.2 Эффекты замены и доходаСкачать

Экономика доступным языком:ЭластичностьСкачать

3.7 Эластичность спроса по цене ч.2Скачать

41 Определение равновесия по ВальрасуСкачать

3.4 ЭластичностьСкачать

2.1.2. Индивидуальный и рыночный спросСкачать






















































































