Уравнение состояния реального газа по сравнению с уравнением состояния идеального газа учитывает

Уравнение описывает поведение реальных газов при не слишком высоких давлениях и при достаточно высоких температурах. В действительности, при давлениях порядка 200 атм наблюдаются значительные отклонения от этого закона, которые, непрерывно возрастая с увеличением давления, достигают при 1000 атм более 100%. При выводе уравнения состояния идеального газа не принимались во внимание размеры молекул и их взаимодействие друг с другом. Между тем при повышении давления возрастает плотность газа, что приводит к уменьшению среднего расстояния между молекулами, вследствие чего размерами молекул и их взаимодействием пренебрегать уже нельзя. Размеры молекулы имеют порядок 10 -8 см. Тогда для объема одной молекулы получим:

Умножая эту величину на число Лошмидта (число молекул в 1 cм&sup3), имеем объем молекул, находящихся в 1 cм&sup3 при нормальных условиях:

Такой величиной действительно можно пренебречь по сравнению с объемом газа в 1 cм&sup3. Однако, если увеличить давление до 5000 атм, то в 5000 раз должна возрасти плотность газа, и их объем в 1 cм&sup3 составит уже 0,5 cм&sup3. Доступным для движения молекул оказался бы объем, в два раза меньший, чем при нормальных условиях. Совершенно очевидно, что обратная пропорциональность объема газа давлению неизбежно должна нарушаться.

Самым простым и дающим хорошие результаты по писанию поведения реальных газов оказалось уравнение Ван-дер-Ваальса, полученное путем введения поправок в уравнение состояния идеального газа pV_км = RT:

где р — давление, оказываемое на газ извне и равное давлению газа на стенки сосуда, а и b — константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем.

В системе СИ константа а измеряется в Н·м 4 /кмоль 2 , константа b — в м&sup3/кмоль. Константа b определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров, и равна учетверенному объему молекулы. Пусть в сосуде находится только две молекулы. Центр любой из них не может приблизиться к центру другой на расстояние, меньшее диаметра молекулы d (Рис. 2.2.1).

Рис. 2.2.1. К объяснению физического смысла константы b

Таким образом, для центра этой молекулы оказывается недоступным сферический объем с радиусом d, т.е. объем, равный 8 объемам молекулы. Поскольку принято во внимание парное взаимодействие молекул, в расчете на одну молекулу недоступным оказывается объем, равный учетверенному объему молекулы. В газе молекулы взаимодействуют (сталкиваются) чаще всего попарно, поскольку вероятности столкновения трех и более молекул крайне малы, поэтому приведенное рассуждение справедливо для всего объема газа: константа b равна учетверенному суммарному объему всех молекул. Фактически введением константы b учитывают отталкивание между молекулами, возникающее при их сильном сближении.

Кроме сил отталкивания, между молекулами есть и силы притяжения. Поправка дает внутреннее давление p_i, обусловленное взаимным притяжением молекул друг к другу. Если бы взаимодействие между молекулами вдруг прекратилось бы, то для того, чтобы удержать газ в пределах заданного объема потребовалось бы увеличить внешнее давление на величину p_i. Обратная пропорциональность может быть объяснена так. Любая молекула, находящаяся вблизи стенки сосуда, будет иметь с одной стороны (обращенной внутрь сосуда) больше соседей, чем с другой. В результате эта молекула будет испытывать результирующую силу, направленную внутрь сосуда. Давление, которое испытывает пристенный слой молекул со стороны остальных молекул газа, равно силе f, действующей на все молекулы на единице поверхности слоя. Очевидно, что эта сила пропорциональна плотности молекул n. С другой стороны, число молекул N в пристенном слое, испытывающих притяжение, также пропорционально n. Следовательно, p_i∼N·∼n 2 . Так как концентрация молекул обратно пропорциональна объему, занимаемому одним молем газа, то выполняется:

Коэффициент пропорциональности а должен быть измерен, поскольку нет способа точного его вычисления.

Чтобы перейти к произвольной массе газа, учтем, что z = m/μ киломолей газа при тех же условиях занимают в z раз больший объем: V = z·V_км. Используя это обстоятельство, запишем уравнение (2.2.1) так:

Умножив это уравнение на z и вводя обозначения:

придем к уравнению Ван-дер-Ваальса для произвольной массы газа:

Насколько уравнение Ван-дер-Ваальса лучше описывает поведение реальных газов, чем уравнение состояния идеального газа, можно судить по данным для 1 л газообразного азота, занимающего при нормальных условиях объем 1 л при 0°С (Табл. 2.2.1).

Сравнение уравнений состояния для идеального и реального газа

р, атм	pV, атм·л	, атм·л
1	1,000	1,000
100	0,994	1,000
200	1,048	1,009
500	1,390	1,014
1000	2,069	0,893

Как видно из Табл. 2.2.1, уравнение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом. Уравнение (2.2.5) можно представить так:

Получилось кубическое уравнение относительно неизвестной V, коэффициенты которого зависят от давления и температуры. Такое уравнение со свободным членом и вещественными коэффициентами имеет три решения, причем в зависимости от соотношения между коэффициентами либо все три решения будут вещественными, либо одно решение — вещественным, а два других — комплексными. Поскольку объем может быть только вещественной величиной, комплексные решения не имеют физического смысла. На Рис. 2.2.2 показаны изотермы Ван-дер-Ваальса для нескольких значений температур.

Рис. 2.2.2. Изотермы Ван-дер-Ваальса

При температуре Т’ и давлениях в пределах p’₁ до p’₂ коэффициенты в уравнении (2.2.6) таковы, что все три решения оказываются вещественными; при иных давлениях вещественным будет только одно решение. Начиная с определенной, своей для каждого вещества температуры Т_кр ( критической температуры ) при любом давлении вещественным остается только одно решение уравнения (2.2.6). Если повышать температуру, то точки, соответствующие решениям уравнения V’₁, V’₂, V’₃, все больше сближаются, сливаясь при критической температуре в одну точку К, также называемую критической точкой . Для соответствующей изотермы точка К является точкой перегиба. Ей соответствуют три совпадающих вещественных решения уравнения (2.2.6). Касательная к критической изотерме в точке К будет параллельна оси V, так что в этом случае производная . Кроме того, в точке перегиба должна быть равна нулю и вторая производная .

Разрешим уравнение (2.2.1) относительно р:

Дифференцирование (2.2.7) по объему дает:

(2.2.8)

(2.2.9)

В критической точке, т.е. при подстановке Т = Т_кр, V_км = V_км.кр, эти выражения должны обращаться в нуль:

(2.2.10)

(2.2.11)

Совместно с (2.2.7), записанным для точки К:

они образуют три уравнения с тремя неизвестными р_кр, V_км.кр и Т_кр. Решение этой системы уравнений дает:

Таким образом, зная константы Ван-дер-Ваальса а и b, можно найти соответствующие критической точке параметры р_кр, V_км.кр и Т_кр, которые называются критическими величинами . И, наоборот, по известным критическим величинам могут быть найдены значения констант Ван-дер-Ваальса. Из (2.2.13) и (2.2.12) можно получить:

в то время как согласно уравнению состояния идеального газа должно было бы выполняться соотношение:

2.2.2. Внутренняя энергия реального газа

Взаимодействие между молекулами реального газа обусловливает их взаимную потенциальную энергию, которая должна учитываться во внутренней энергии газа наряду с кинетической энергией движения молекул:

Кинетическая энергия киломоля газа равна:

и прямо пропорционально зависит от температуры.

Потенциальная энергия взаимодействия молекул зависит от среднего расстояния между ними, поэтому Е_п должна быть функцией объема газа V. Следовательно, внутренняя энергия газа есть функция двух параметров — температуры и объема:

При расширении газа совершается работа по преодолению сил притяжения между молекулами. Работа против внутренних сил, действующих между молекулами киломоля газа, может быть записана в виде:

Приравнивая (2.2.19) приращению потенциальной энергии, получим:

Интегрируя (2.2.20), имеем:

Значение постоянной интегрирования полагают равной нулю, что при увеличении объема газа до бесконечности соответствует отсутствию взаимодействия между молекулами газа. Тогда полное выражение для внутренней энергии киломоля реального газа будет иметь вид:

Из (2.2.22) следует, что внутренняя энергия растет как при повышении температуры, так и при увеличении объема.

Если газ будет расширяться или сжиматься без теплообмена с внешней средой и без совершения над ним внешней работы, то, согласно первому началу термодинамики, его внутренняя энергия должна оставаться постоянной. Тогда из (2.2.22) получим:

из чего следует, что приращения dT и dV_км имеют противоположный знак.

Следовательно, при расширении в таких условиях газ всегда должен охлаждаться, а при сжатии — нагреваться.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Уравнение состояния вещества

Параметры состояния связаны друг с другом. Соотношение, при котором определяется данная связь, называют уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров: давления p , объема V и температуры (масса тела или системы, как правило, известна).

Что такое идеальный газ

Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.

Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.

Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.

Уравнение состояния идеального газа запишем несколько раз ( 2 ) , ( 3 ) , ( 5 ) :

p V = m μ R T = ν R T ( 2 ) .

Уравнение ( 2 ) – уравнение Менделеева-Клапейрона, где m – это масса газа, μ – это молярная масса газа, R = 8 , 31 Д ж м о л ь · К – это универсальная газовая постоянная, ν – это число молей вещества.

где N – это количество молекул газа в массе m , k = 1 , 38 · 10 — 23 Д ж К , постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и

N A = 6 , 02 · 10 23 м о л ь — 1 – это постоянная Авогадро.

Если поделить в ( 4 ) обе части на V , то получаем следующий вид записи уравнения состояния идеального газа:

где n = N V – это количество частиц в единице объема или же концентрация частиц.

Что такое реальный газ

Рассмотрим теперь более сложные системы: неидеальные газы и жидкости.

Реальный газ – это газ, между молекулами которого наблюдаются заметные силы взаимодействия.

Необходимо учитывать, что в неидеальных, плотных газах взаимодействие молекул высоко. Известно, что взаимодействие молекул очень сильно усложняет физическую картину, потому точную формулу уравнения состояния неидеального газа не получается записать в простом виде. В данном случае прибегают к приближенным формулам, найденным полу-эмпирическим путем. Самая удачная формула – это уравнение Ван-деp-Ваальса.

Взаимодействие молекул обладает сложным характером. На достаточно больших расстояниях между молекулами действуют силы притяжения. С уменьшением расстояния силы притяжения вначале растут, однако потом уменьшаются и преобразуются в силы отталкивания. Притяжение и отталкивание молекул будем рассматривать и учитывать отдельно. Уравнение Ван-дер-Ваальса, которое описывает состояние одного моля реального газа, имеет вид:

p + a V μ 2 V μ — b = R T ( 6 ) ,

где a V μ 2 – это внутреннее давление, обусловленное силами притяжения между молекулами, b – это поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами, при этом:

b = N A 2 3 πd 3 ( 7 ) ,

где d – это диаметр молекулы. Значение a рассчитывается по формуле:

a = — 2 πN A 2 ∫ d ∞ W p ( r ) r 2 dr ( 8 ) ,

где W p ( r ) – это потенциальная энергия притяжения 2 -х молекул.

При увеличении объема значение поправок в уравнении ( 6 ) становится менее существенным. И в пределе уравнение ( 6 ) превращается в уравнение ( 2 ) . Это согласовано с тем фактом, что с уменьшением плотности реальные газы по своим характеристикам приближаются к идеальным.

Положительным в уравнении Ван-деp-Ваальса является тот факт, что данное равенство при очень больших плотностях приблизительно описывает также и свойства жидкости, в частности, плохую ее сжимаемость. Потому существует основание предполагать, что уравнение Ван-деp-Ваальса позволяет отразить и переход от жидкости к газу (либо от газа к жидкости).

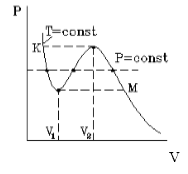
На рисунке 1 представлена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T , которая построена из соответствующего уравнения.

В месте “извилины” (участок КМ) изотерма 3 раза пересекает изобару. На участке
V 1 , V 2 давление увеличивается с ростом объема.

Подобная зависимость невозможна. Это означает, что в этой области с веществом происходит что-то необыкновенное. Что именно, не видно в уравнении Ван-деp-Ваальса. Обратимся к опыту. В месте “извилины” на изотерме в состоянии равновесия вещество расслаивается на 2 фазы: жидкую и газообразную. Обе фазы существуют одновременно и находятся в фазовом равновесии. В таком состоянии происходит испарение жидкости и конденсация газа. Процессы протекают с такой интенсивностью, что полностью компенсируют друг друга: объем жидкости и газа со временем не изменяется.

Газ, который находится в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазовое равновесие отсутствует, отсутствует также компенсация испарения и конденсации, тогда газ называется ненасыщенным паром.

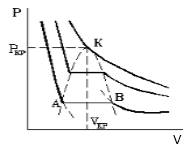
Что происходит с изотермой в области двухфазного состояния вещества (то есть в месте «извилины» изотермы Ван-деp-Ваальса)? Эксперимент показывает, что в этом месте при изменении объема давление остается неизменным. График изотермы идет параллельно оси V (рисунок 2 ).

С увеличением температуры участок двухфазных состояний на изотермах уменьшается до тех пор, пока не превращается в точку (рисунок 2 ). Это особая точка К , в которой исчезает разница между жидкостью и паром. Ее называют критической точкой.

Параметры, которые соответствуют критическому состоянию, являются критическими (критическая температура, критическое давление, критическая плотность вещества).

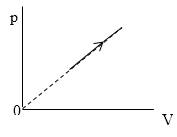
Необходимо найти величину n . В процессе, представленном на рисунке 3 , давление p

Из графика, приведенного на рисунке 3 , запишем уравнение процесса в параметрах p ( V ) :

С учетом уравнения Менделеева-Клайперона:

V вместо объема, получаем:

Моль кислорода охлаждают до — 100 ° C . Необходимо определить давление, которое оказывает газ на стенки сосуда, если занимаемый газом объем V = 0 , 1 л . Необходимо также сравнить p с давлением идеального газа p i d , если бы кислород вел себя как идеальный газ. Величина постоянных Ван-дер-Ваальса a и b , для кислорода a = 0 , 1358 П а · м 6 / м о л ь 2 , b = 3 , 167 · 10 — 5 м 3 / м о л ь .

Из уравнения Ван-Дер-Ваальса имеем:

p = R T V μ — b — a V μ 2

Переведем температуру в систему измерения: T = t + 273 , По условию T = 173 K , V = 0 , 1 л = 10 — 4 м 3 .

Произведем расчет: p = 8 , 31 · 173 ( 10 — 3 , 2 ) · 10 — 5 — 0 , 1358 ( 10 — 4 ) 2 = 75 , 61 · 10 5 ( П а ) .

Для идеального газа:

Рассчитаем: p i d = 1 · 8 , 31 · 173 10 — 4 = 143 · 10 5 ( П а ) .

Уравнения состояния реальных газов

Вопрос №1

Идеальный газ. Законы идеальных газов

Идеальным называется газ, у которого объемы молекул беско­нечно малы и отсутствуют силы межмолекулярного взаимодей­ствия. Молекулы идеального газа представляют собой материаль­ные точки, взаимодействие между которыми ограничено молеку­лярными соударениями.

Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воз­дух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

На практике часто приходится иметь дело с газами при невы­соких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.

Закон Авогадро

Согласно этому закону, все газы при одинаковых температу­рах и одинаковом давлении содержат в одном и том же объеме оди­наковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных га­зов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м 3 /кмоль.Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.

Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведе­ние давления газа на его объем есть величина постоянная, т.е. при

рV= const и рv = const.

Закон Гей-Люссака

Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если

Р = const, то и v/ Т = const.

Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.

Уравнение состояния идеального газа

Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид

Для одного киломоля вещества уравнение состояния (получе­но Д.И. Менделеевым) имеет вид рV_µ =µRT, где µR— универсаль­ная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.

Во всех этих уравнениях давление подставляется в Па, темпе­ратура — в К, объем — в м 3 и удельный объем — в м 3 /кг.

В резервуаре объемом 10 м 3 находится азот при из­быточном давлении 100 кПа и при температуре 27 °С. Атмосфер­ное давление равно 750 мм рт. ст. Требуется найти массу и плот­ность азота.

Выразим атмосферное давление в паскалях: р_б = 10 5 Па.

Абсолютное давление газа равно:p =р_и +р_б = 100 • 10 3 + 10 5 = = 2 • 10 5 Па.

Газовая постоянная азота равна (µ = 28 кг/кмоль)

R = 8314/28 = 297 Дж/кгЧК. Масса газа равна

М =рV/RT= 2*10 5* 10/297 • (273,15 + 27) = 22,43 кг.

р = M/V= 22,43/10 = 2,243 кг/м 3 .

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РЕАЛЬНЫЕ ГАЗЫ

Свойства реальных газов

Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше дав­ление и ниже температура газа. Это объясняется тем, что молеку­лы реальных газов имеют конечный объем и между ними существу­ют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид

где z= φ(р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.

При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энталь­пии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависи­мости от температуры может находиться в разных состояниях.

Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния бу­дем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.

При определенных условиях могут существовать одновремен­но две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.

У всех веществ фазовые переходы происходят при определен­ных физических параметрах, поэтому рассмотрение свойств реаль­ных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.

Рассмотрим диаграмму «v—p» воды и во­дяного пара, на которой изобразим грани­цы между фазами (рис. 1.1). В области а нахо­дится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый во­дяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.

Показанные на рис. 1.1 кривые называют­ся пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насы­щенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухо­го насыщенного пара и кипящей воды называют влажным насы­щенным паром. Масса влажного насыщенного пара равна

где М’ — масса кипящей воды и М» — масса сухого насыщенного пара.

В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р’, h’и т.д.), а все параметры, от­носящиеся к сухому насыщенному пару,— индекс «два штри­ха» (р’, h» и т.д.).

Температуру и давление насыщенного пара принято обозна­чать Т_н и р_н. В то же время в ряде литературных источников их обозначают Т_s и р_s (буква s является первой буквой английского слова sаturation — насыщение). Отношение массы сухого насыщен­ного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой погранич­ной кривой х = 0, а на правой — х = 1. Разность <1-х) называется степенью влажности.

Чем выше давление пара, тем меньше расстояние по горизон­тали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насы­щенного пара, называется критической (точка к на рис. 1.1).

Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведе­ны в табл. 1

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Таблица 1 Критические параметры веществ

Вещество	Tкр, К	pкр,МПа	ρкр, кг/м 3
Азот N2	3,40
Водород Н2	33,2	1,29
Водяной пар H2O	647,12	22,115
Кислород О2	5,05
Ртуть Нg	—
Диоксид углерода СО2	7,38

При сверхкритическом давлении не может быть влажного на­сыщенного пара. Если давление пара больше критического и по­стоянно по величине (р > ркр), то при подводе (или отводе) тепло­ты физические параметры (удельный объем, энтальпия и др.) меня­ются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода перехо­дит в сверхперегретый водяной пар.

Уравнения состояния реальных газов

Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде

Слагаемое a/v 2 учитывает внутреннее давление, обусловлен­ное силами взаимодействия молекул газа, а величина b— умень­шение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объе­мов реальных газов, то уравнение (1) имеет три действительных корня при Т Ткр . Точность вычислений по этому уравнению невелика.

В самой общей форме уравнение состояния реальных газов имеет вид

(2)

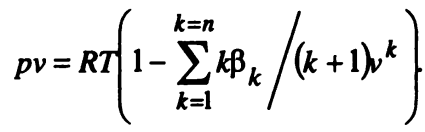
где 𝛽_k — вириальные коэффициенты, зависящие от температуры газа.

Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значитель­ные трудности.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

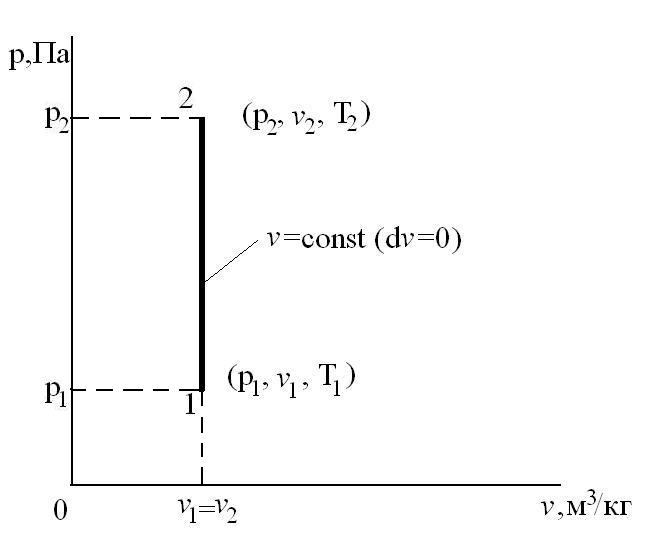
Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.

Этот процесс используется как подготовительный процесс в циклах.

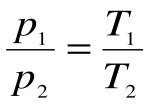
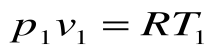
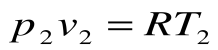
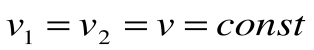
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: , который следует из уравнений состояния для точек 1 и 2:

и при .

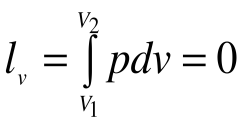
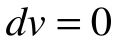
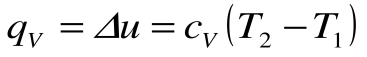
Поскольку работа расширения в этом процессе равна нулю: , т.к. , то из уравнения 1-го закона термодинамики следует, что:

.

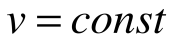
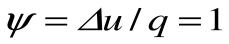
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП коэффициент распределения теплоты , теплоемкость и показатель политропы:

.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

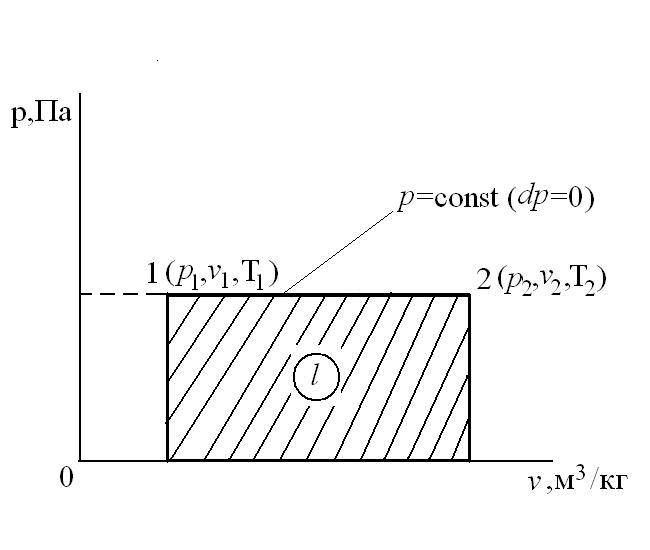
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.

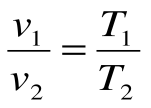
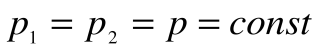
Соотношение между параметрами в процессе р=const: — закон Гей-Люссака, т.к.: , и .

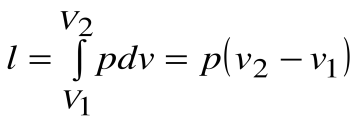
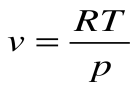
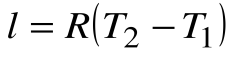
Работа расширения . Т.к. , то .

Следовательно, удельная газовая постоянная R— это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:

.

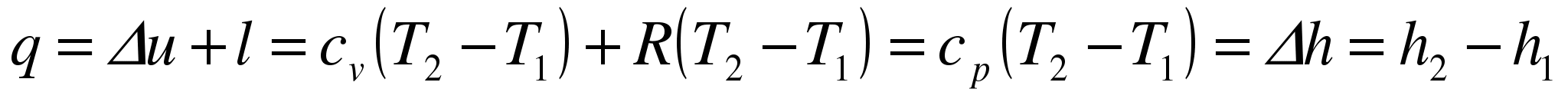
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.

Коэффициент распределения теплоты в процессе р=const равен:

, .

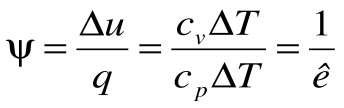
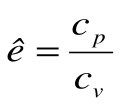
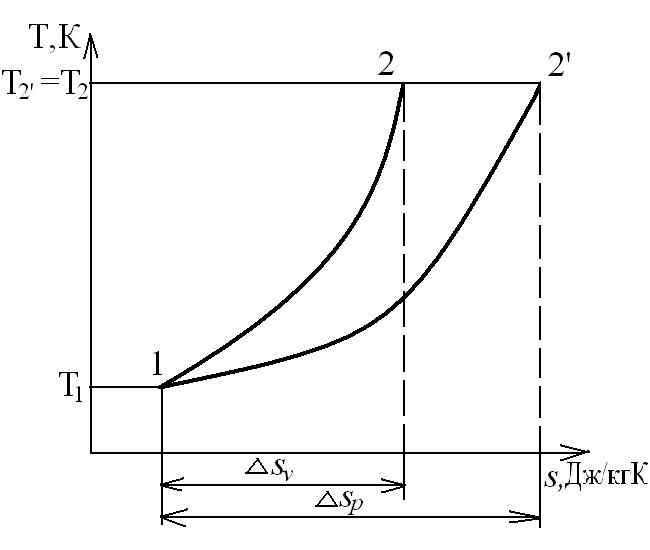
В T-s координатах взаимное положение изобары и изохоры имеет вид:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

, , т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.

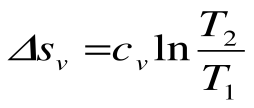
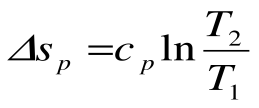
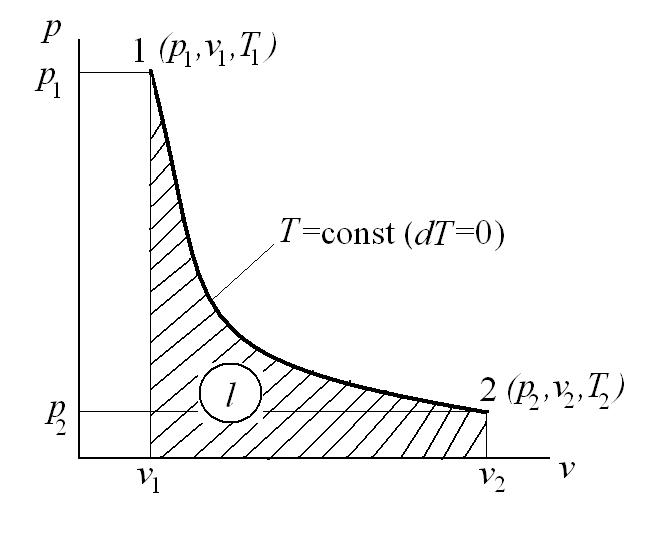
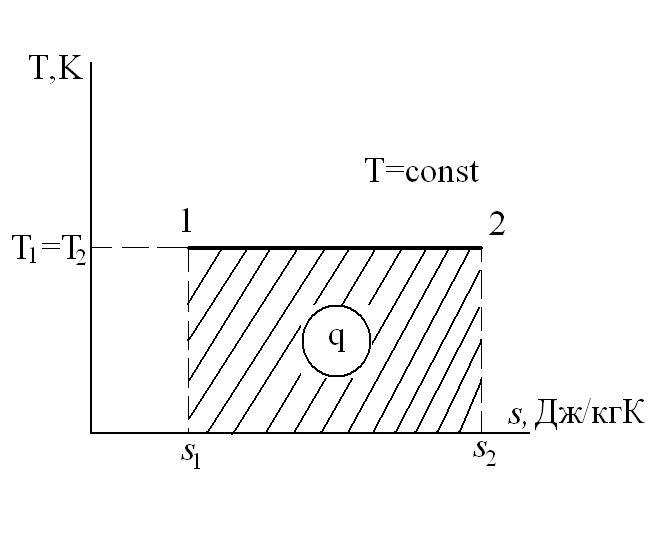
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре

При Т=const из уравнения состояния имеем: — это уравнение изотермического процесса является уравнением равнобокой гиперболы.

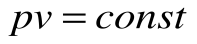
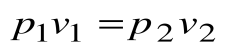
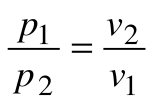
Тогда , и — закон Бойля-Мариотта.

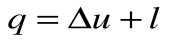
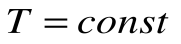
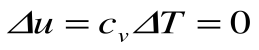
Из уравнения 1-го закона термодинамики при имеем:

и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.

Изменение энтальпии в процессе T=const равно:

.

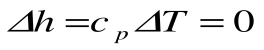
Изм.

Лист

№ докум.

Подпись

Дата

Лист

Работа расширения .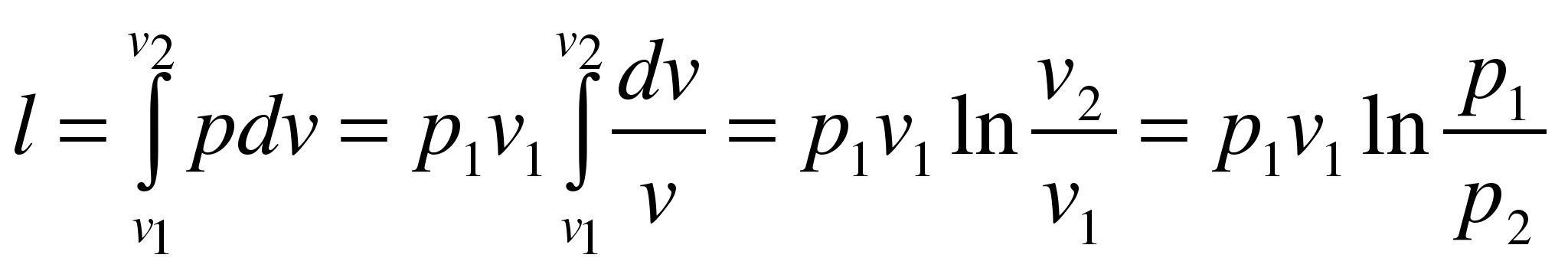

Коэффициент распределения теплоты

.

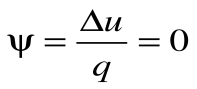
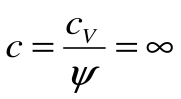
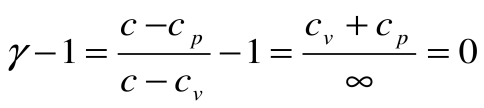
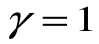
Тогда теплоемкость и показатель политропы для процесса T=const будет равен , т.е. .

Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и 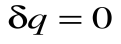(на конечном и бесконечно малом участке процесса).

Если записать для этого случая уравнения 1-го закона термодинамики в виде:

1. или ,

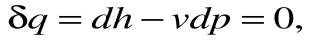
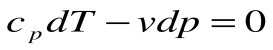
2. или , то после деления (1) на (2) получим:

— показатель адиабаты.

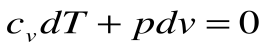
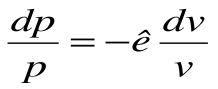
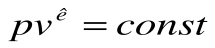
Тогда после интегрирования выражения для конечного процесса 1-2 будем иметь , или — это есть уравнение адиабатного процесса в p-v-координатах, которое является уравнением неравнобокой гиперболы.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

, т.к. Т , то ds=0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.

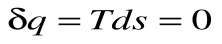
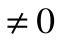
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т₁ и Т₂.

Рассмотрим прямой цикл Карно.

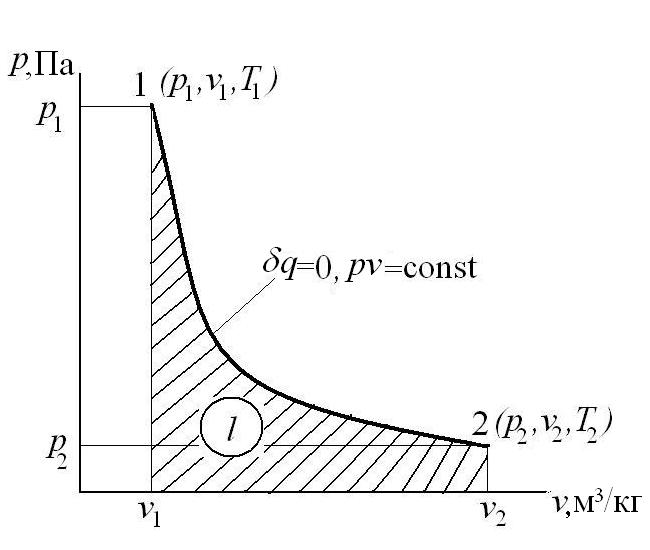
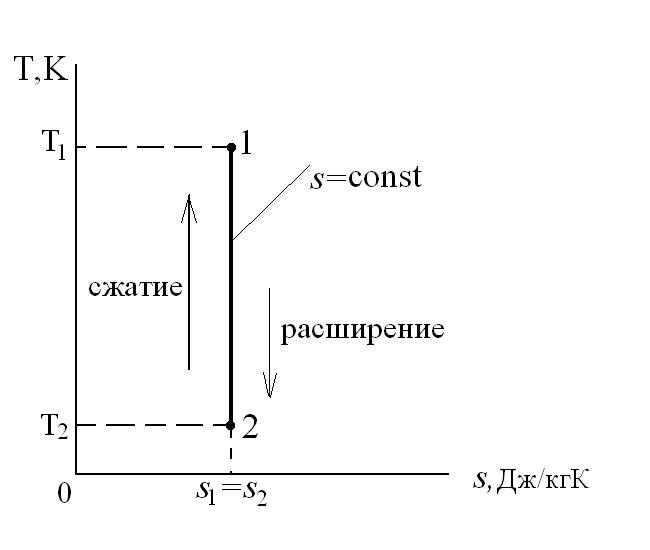
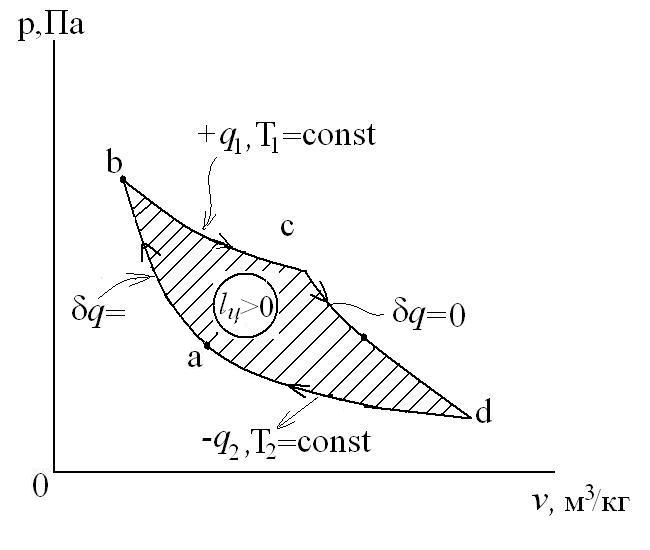
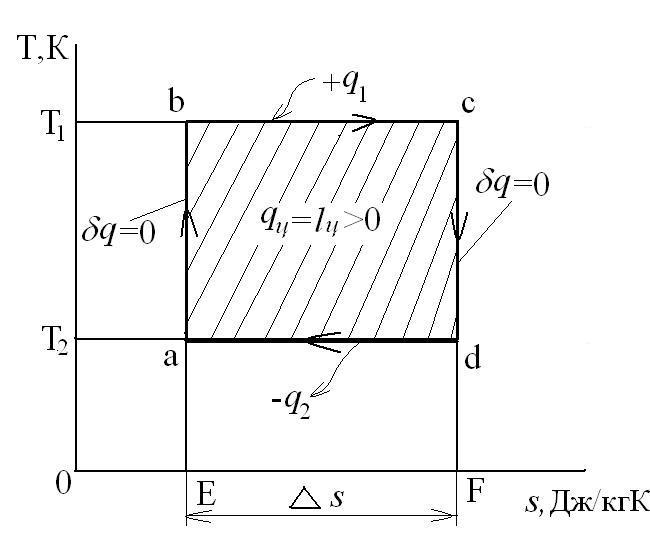
Графически в p-v и T-s координатах этот цикл можно представить в виде:

где ab – адиабатное сжатие ТРТ;

bc – подвод теплоты q₁ в изотермическом процессе при Т₁=const;

cd – адиабатное расширение ТРТ;

da – отвод теплоты 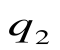в холодильник при Т₂=const;

q₁ = площадь bсFEb – теплота, затраченная на совершение цикла .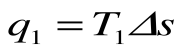

q₂ = площадь adFЕa – теплота, отведенная в холодильник .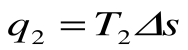

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Тогда термический кпд прямого цикла Карно будет равен:

.

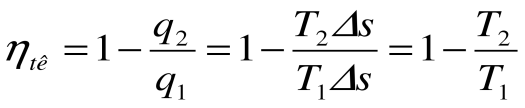
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т₁ и Т₂ являются основными параметрами цикла Карно, которые полностью определяют этот цикл.

При Т₁=Т₂ термический кпд цикла Карно 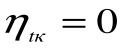, т.е. превращение теплоты в работу невозможно.

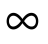
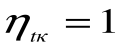
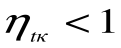
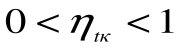
При Т₂=0 или Т₁= , что невыполнимо. Следовательно, в цикле Карно термический кпд цикла всегда меньше единицы: . Таким образом, для прямого цикла Карно .

Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.

В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В– водород, объем сосуда А– 150 л, сосуда В – 250 л. Давление и температура аргона – р₁, t₁, водорода – р₂, t₂. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь

📸 Видео