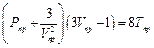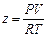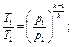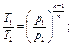Уравнение состояния отклонения реальных газов от законов идеального газа

Как известно, уравнение состояния устанавливает функциональную связь между давлением p, объемом V, температурой T и числом молей n газа в состоянии равновесия. Эта связь может выражаться не только в форме уравнения, но также графически или в виде таблиц, которые часто используются, особенно для практических целей. Самым простым и известным уравнением состояния является уравнение состояния идеального газа:

где R – универсальная газовая постоянная.

Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации.

Так, для газов с низкой температурой сжижения (He, H₂, Ne и даже N₂, O₂, Ar, CO, CH₄) при давлениях до 50 атм отклонения не превышают 5%, а при давлениях до 10 атм – 2%. Легко конденсирующиеся газы (CO₂, SO₂, Cl₂, CH₃Cl) уже при 1 атм обнаруживают отклонения до 2 – 3%.

Одной из наглядных характеристик отклонений реальных газов от идеального поведения оказывается мольный объем газа V_m = V/n. Для идеального газа он равен 22,414 л при 1 атм и 273 K. Значения V_m для некоторых реальных газов представлены в таблице 1.1.

Таблица 1.1. Мольные объемы газов при 1 атм и 273 K

Газ	Vm, л* моль -1	Газ	Vm, л* моль -1
H2	22,43	CO2	22,26
He	22,43	N2O	22,25
Ne	22,42	H2O	22,14
F2	22,42	NH3	22,08
N2	22,40	Cl2	22,02
CO	22,40	SO2	21,89
O2	22,39	C4H10	21,50
CH4	22,36	O3	21,60

Наиболее удобной мерой неидеальности является фактор сжимаемости Z = pV_m/RT, поскольку для идеального газа Z = l при любых условиях.

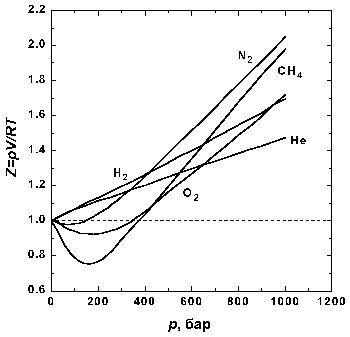
Рис.1.1 Зависимость фактора сжимаемости некоторых газов от давления при 298 К.

На рис. 1.1 представлены факторы сжимаемости для некоторых реальных газов как функции давления при 298 К (для сравнения поведение идеального газа показано пунктиром). При высоких давлениях для всех газов Z > 1, т.е. их труднее сжать, чем идеальный газ, поскольку в этой области преобладают силы межмолекулярного отталкивания. Из рисунка видно, что при более низких давлениях для некоторых газов Z

Рис1.2. Зависимость фактора сжимаемости N₂ от давления при разных температурах.

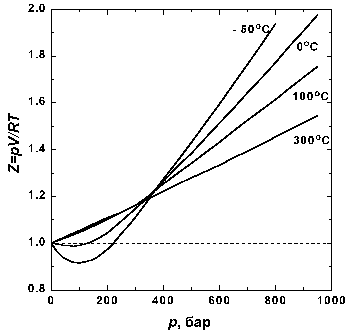
На рис. 1.2 представлены факторы сжимаемости для азота при разных температурах. По мере уменьшения температуры эффект межмолекулярного притяжения увеличивается (что проявляется в образовании минимума на кривых в области давлений около 100 бар). Минимум на кривых обнаруживается для всех газов, если температура достаточно низка. У водорода и гелия, имеющих очень низкие температуры кипения, этот минимум наблюдается только при температурах значительно ниже 0° C.

Из приведенных данных видно, что при низких давлениях реальные газы могут быть более сжимаемыми (Z 1). Очевидно, что основными причинами отклонений свойств реальных газов от свойств идеального газа оказываются взаимное притяжение молекул и наличие у них собственного объема. Наиболее ярко межмолекулярное притяжение в реальных газах проявляется в их способности к конденсации – переходу в жидкое состояние.

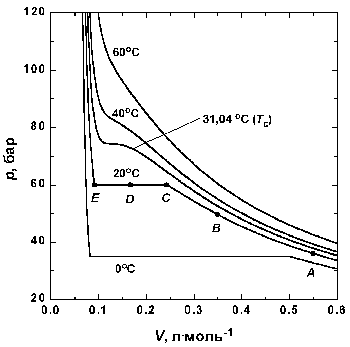
Рассмотрим, что происходит, когда образец газа в состоянии, отмеченном точкой А на рис. 1.3, сжимается при постоянной температуре.

Рис 1.3. Экспериментальные изотермы для СО₂

Вблизи точки А давление возрастает приблизительно по закону Бойля. Заметные отклонения от закона Бойля начинают наблюдаться, когда объем становится соизмеримым со значением, указанным точкой В.

В точке С сходство с идеальным поведением полностью теряется, так как оказывается, что дальнейшее уменьшение объема не вызывает роста давления; это показано горизонтальной линией CDE. Исследование содержания сосуда показывает, что сразу за точкой С появляется жидкость, и можно наблюдать две фазы, разделенные резко обозначенной границей – поверхностью раздела. Поскольку при уменьшении объема газ конденсируется, он не оказывает сопротивления дальнейшему движению поршня. Давление, соответствующее линии CDE, когда жидкость и пар находятся в равновесии, называется давлением пара жидкости при температуре опыта.

В точке Е весь образец представляет собой жидкость, и дальнейшее уменьшение объема образца требует значительного давления, поскольку жидкости по сравнению с газами очень трудно сжимаются, что проявляется в резком подъеме кривой слева от точки Е.

1.2. Критические явления

Изотерма при температуре T_c играет особую роль в теории состояния вещества. Изотерма, соответствующая температуре ниже T_c, ведет себя так, как уже описано: при определенном давлении газ конденсируется в жидкость, которую можно различать по наличию поверхности раздела. Если же сжатие осуществлять при T_c, то поверхность, разделяющая две фазы, не появляется, а точка конденсации и точка полного перехода в жидкость сливаются в одну критическую точку газа. При температуре выше T_c газ невозможно обратить в жидкость никаким сжатием. Температура, давление и мольный объем в критической точке называются критической температурой T_c, критическим давлением p_c и критическим мольным объемом V_c вещества. Собирательно параметры p_c, V_c, и T_c называются критическими константами данного газа (таблица 1.2).

Таблица 1.2. Критические константы и температуры Бойля

Газ	Tc, K	Pc, бар	Vc, мл* моль -1	Zc	TB, K	TB/Tc
He	5,21	2,27	57,76	0,305	22,64	4,35
Ne	44,44	26,9	41,74	0,307	122,1	2,75
Ar	150,72	48,0	75,25	0,292	411,5	2,73
Kr	209,4	54,3	92,24	0,291	575,0	2,75
Xe	289,75	58,0	118,8	0,290	768,0	2,65
H2	33,3	13,0	65,0	0,306	110,0	3,30
N2	126,1	34,0	89,5	0,292	327,2	2,60
O2	154,4	50,5	73,4	0,292	405,9	2,63
CO2	304,2	73,8	94,0	0,274	714,8	2,35
CH4	190,7	46,0	99,0	0,287	510,0	2,67
C2H4	282,4	50,4	129,0	0,277	624	2,21

При T T_c образец представляет собой фазу, полностью занимающую объем содержащего ее сосуда, т. е. по определению является газом. Однако плотность этой фазы может быть значительно большей, чем это типично для газов, поэтому обычно предпочитают название «сверхкритический флюид» (supercritical fluid).

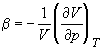
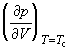
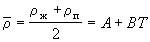
В критической точке изотермический коэффициент сжимаемости равен бесконечности, поскольку = 0. Поэтому вблизи критической точки сжимаемость вещества так велика, что ускорение силы тяжести приводит к значительным различиям плотности в верхней и нижней частях сосуда, достигающим 10% в столбике вещества высотой всего несколько сантиметров. Это затрудняет определение плотностей (удельных объемов) и, соответственно, изотерм p – V вблизи критической точки. В то же время критическую температуру можно определить весьма точно как такую температуру, при которой поверхность, разделяющая газообразную и жидкую фазы, исчезает при нагревании и вновь появляется при охлаждении. Зная критическую температуру, можно определить критическую плотность (и, соответственно, критический мольный объем), пользуясь эмпирическим правилом прямолинейного диаметра (правило Кальете-Матиаса), согласно которому средняя плотность жидкости и насыщенного пара является линейной функцией температуры:

, (1.2)

где A и B – постоянные для данного вещества величины. Экстраполируя прямую средней плотности 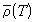до критической температуры, можно определить критическую плотность (см. задачу 1.7).

Высокая сжимаемость вещества вблизи критической точки приводит к росту спонтанных флуктуаций плотности, которые сопровождаются аномальным рассеянием света. Это явление называется критической опалесценцией.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Уравнение состояния отклонения реальных газов от законов идеального газа

Уравнение описывает поведение реальных газов при не слишком высоких давлениях и при достаточно высоких температурах. В действительности, при давлениях порядка 200 атм наблюдаются значительные отклонения от этого закона, которые, непрерывно возрастая с увеличением давления, достигают при 1000 атм более 100%. При выводе уравнения состояния идеального газа не принимались во внимание размеры молекул и их взаимодействие друг с другом. Между тем при повышении давления возрастает плотность газа, что приводит к уменьшению среднего расстояния между молекулами, вследствие чего размерами молекул и их взаимодействием пренебрегать уже нельзя. Размеры молекулы имеют порядок 10 -8 см. Тогда для объема одной молекулы получим:

Умножая эту величину на число Лошмидта (число молекул в 1 cм&sup3), имеем объем молекул, находящихся в 1 cм&sup3 при нормальных условиях:

Такой величиной действительно можно пренебречь по сравнению с объемом газа в 1 cм&sup3. Однако, если увеличить давление до 5000 атм, то в 5000 раз должна возрасти плотность газа, и их объем в 1 cм&sup3 составит уже 0,5 cм&sup3. Доступным для движения молекул оказался бы объем, в два раза меньший, чем при нормальных условиях. Совершенно очевидно, что обратная пропорциональность объема газа давлению неизбежно должна нарушаться.

Самым простым и дающим хорошие результаты по писанию поведения реальных газов оказалось уравнение Ван-дер-Ваальса, полученное путем введения поправок в уравнение состояния идеального газа pV_км = RT:

где р — давление, оказываемое на газ извне и равное давлению газа на стенки сосуда, а и b — константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем.

В системе СИ константа а измеряется в Н·м 4 /кмоль 2 , константа b — в м&sup3/кмоль. Константа b определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров, и равна учетверенному объему молекулы. Пусть в сосуде находится только две молекулы. Центр любой из них не может приблизиться к центру другой на расстояние, меньшее диаметра молекулы d (Рис. 2.2.1).

Рис. 2.2.1. К объяснению физического смысла константы b

Таким образом, для центра этой молекулы оказывается недоступным сферический объем с радиусом d, т.е. объем, равный 8 объемам молекулы. Поскольку принято во внимание парное взаимодействие молекул, в расчете на одну молекулу недоступным оказывается объем, равный учетверенному объему молекулы. В газе молекулы взаимодействуют (сталкиваются) чаще всего попарно, поскольку вероятности столкновения трех и более молекул крайне малы, поэтому приведенное рассуждение справедливо для всего объема газа: константа b равна учетверенному суммарному объему всех молекул. Фактически введением константы b учитывают отталкивание между молекулами, возникающее при их сильном сближении.

Кроме сил отталкивания, между молекулами есть и силы притяжения. Поправка дает внутреннее давление p_i, обусловленное взаимным притяжением молекул друг к другу. Если бы взаимодействие между молекулами вдруг прекратилось бы, то для того, чтобы удержать газ в пределах заданного объема потребовалось бы увеличить внешнее давление на величину p_i. Обратная пропорциональность может быть объяснена так. Любая молекула, находящаяся вблизи стенки сосуда, будет иметь с одной стороны (обращенной внутрь сосуда) больше соседей, чем с другой. В результате эта молекула будет испытывать результирующую силу, направленную внутрь сосуда. Давление, которое испытывает пристенный слой молекул со стороны остальных молекул газа, равно силе f, действующей на все молекулы на единице поверхности слоя. Очевидно, что эта сила пропорциональна плотности молекул n. С другой стороны, число молекул N в пристенном слое, испытывающих притяжение, также пропорционально n. Следовательно, p_i∼N·∼n 2 . Так как концентрация молекул обратно пропорциональна объему, занимаемому одним молем газа, то выполняется:

Коэффициент пропорциональности а должен быть измерен, поскольку нет способа точного его вычисления.

Чтобы перейти к произвольной массе газа, учтем, что z = m/μ киломолей газа при тех же условиях занимают в z раз больший объем: V = z·V_км. Используя это обстоятельство, запишем уравнение (2.2.1) так:

Умножив это уравнение на z и вводя обозначения:

придем к уравнению Ван-дер-Ваальса для произвольной массы газа:

Насколько уравнение Ван-дер-Ваальса лучше описывает поведение реальных газов, чем уравнение состояния идеального газа, можно судить по данным для 1 л газообразного азота, занимающего при нормальных условиях объем 1 л при 0°С (Табл. 2.2.1).

Сравнение уравнений состояния для идеального и реального газа

р, атм	pV, атм·л	, атм·л
1	1,000	1,000
100	0,994	1,000
200	1,048	1,009
500	1,390	1,014
1000	2,069	0,893

Как видно из Табл. 2.2.1, уравнение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом. Уравнение (2.2.5) можно представить так:

Получилось кубическое уравнение относительно неизвестной V, коэффициенты которого зависят от давления и температуры. Такое уравнение со свободным членом и вещественными коэффициентами имеет три решения, причем в зависимости от соотношения между коэффициентами либо все три решения будут вещественными, либо одно решение — вещественным, а два других — комплексными. Поскольку объем может быть только вещественной величиной, комплексные решения не имеют физического смысла. На Рис. 2.2.2 показаны изотермы Ван-дер-Ваальса для нескольких значений температур.

Рис. 2.2.2. Изотермы Ван-дер-Ваальса

При температуре Т’ и давлениях в пределах p’₁ до p’₂ коэффициенты в уравнении (2.2.6) таковы, что все три решения оказываются вещественными; при иных давлениях вещественным будет только одно решение. Начиная с определенной, своей для каждого вещества температуры Т_кр ( критической температуры ) при любом давлении вещественным остается только одно решение уравнения (2.2.6). Если повышать температуру, то точки, соответствующие решениям уравнения V’₁, V’₂, V’₃, все больше сближаются, сливаясь при критической температуре в одну точку К, также называемую критической точкой . Для соответствующей изотермы точка К является точкой перегиба. Ей соответствуют три совпадающих вещественных решения уравнения (2.2.6). Касательная к критической изотерме в точке К будет параллельна оси V, так что в этом случае производная . Кроме того, в точке перегиба должна быть равна нулю и вторая производная .

Разрешим уравнение (2.2.1) относительно р:

Дифференцирование (2.2.7) по объему дает:

(2.2.8)

(2.2.9)

В критической точке, т.е. при подстановке Т = Т_кр, V_км = V_км.кр, эти выражения должны обращаться в нуль:

(2.2.10)

(2.2.11)

Совместно с (2.2.7), записанным для точки К:

они образуют три уравнения с тремя неизвестными р_кр, V_км.кр и Т_кр. Решение этой системы уравнений дает:

Таким образом, зная константы Ван-дер-Ваальса а и b, можно найти соответствующие критической точке параметры р_кр, V_км.кр и Т_кр, которые называются критическими величинами . И, наоборот, по известным критическим величинам могут быть найдены значения констант Ван-дер-Ваальса. Из (2.2.13) и (2.2.12) можно получить:

в то время как согласно уравнению состояния идеального газа должно было бы выполняться соотношение:

2.2.2. Внутренняя энергия реального газа

Взаимодействие между молекулами реального газа обусловливает их взаимную потенциальную энергию, которая должна учитываться во внутренней энергии газа наряду с кинетической энергией движения молекул:

Кинетическая энергия киломоля газа равна:

и прямо пропорционально зависит от температуры.

Потенциальная энергия взаимодействия молекул зависит от среднего расстояния между ними, поэтому Е_п должна быть функцией объема газа V. Следовательно, внутренняя энергия газа есть функция двух параметров — температуры и объема:

При расширении газа совершается работа по преодолению сил притяжения между молекулами. Работа против внутренних сил, действующих между молекулами киломоля газа, может быть записана в виде:

Приравнивая (2.2.19) приращению потенциальной энергии, получим:

Интегрируя (2.2.20), имеем:

Значение постоянной интегрирования полагают равной нулю, что при увеличении объема газа до бесконечности соответствует отсутствию взаимодействия между молекулами газа. Тогда полное выражение для внутренней энергии киломоля реального газа будет иметь вид:

Из (2.2.22) следует, что внутренняя энергия растет как при повышении температуры, так и при увеличении объема.

Если газ будет расширяться или сжиматься без теплообмена с внешней средой и без совершения над ним внешней работы, то, согласно первому началу термодинамики, его внутренняя энергия должна оставаться постоянной. Тогда из (2.2.22) получим:

из чего следует, что приращения dT и dV_км имеют противоположный знак.

Следовательно, при расширении в таких условиях газ всегда должен охлаждаться, а при сжатии — нагреваться.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Отклонения реальных газов от физических законов

Законы газового состоянии справедливы для идеальных газов. Все существующие в действительности реальные газы более или менее отклоняются от идеальных газов. При этом отклонение тем больше, чем ниже температура и выше давление.

Такие газы, как водород, азот, кислород, так называемые действительные или постоянные газы при обычных условиях приближаются к идеальным. Вообще при нормальных температурах и давлении отклонение от идеальных газов меньше у тех газов, у которых критическая температура очень низка, а критическое давление велико. Для таких газов почти полностью справедливо выражение PV=const. Реальные газы следуют этому закону приблизительно и то при низких давлениях. Для реальных газов уравнение состояния газа PV=RT является предельным, т. е. становится справедливым только при Р→0.

Причина отклонения реальных газов от законов газового состояния заключается в следующем.

Законы газового состояния были введены при допущении, что молекулы газа можно рассматривать как материальные точки, размep которых ничтожно мал по сравнению с пространством между ними, и что между молекулами газа не действуют межмолекулярные силы. Между тем у реальных газов молекулы занимают некоторый объем, вследствие чего часть объема занята самими молекулами, и между ним действуют силы сцепления.

Было сделано много попыток опытным путем или теоретически обобщить отклонения реальных газов от законов газового состояния. Из всех попыток наибольшего внимания заслуживает уравнение Ван-дер-Ваальса, согласно которому в уравнение состояния газа PV=RT введены поправки на объем, занимаемый молекулами, и на силы взаимодействия между ними (внутреннее давление). Уравнение, Ван-дер-Ваальса имеет следующий вид

(1.14)

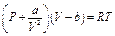
где 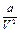— выражает внутреннее давление молекул, которое является равнодействующей сил их взаимного притяжения в объеме V; b — поправка на объем, которая при допущении шарообразности молекул равна учетверенному объему самих молекул.

Постоянные а и b приведенного уравнения могут быть вычислены из критических условий по следующим соотношениям:

;

;

.

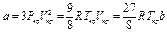
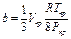
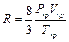
Если вместо параметров Р, V и Т ввести приведенные параметры и выразить константы aи bчерез критические параметры, то уравнение (1.14) может быть преобразовано в обобщенное уравнение, одинаковое для любого газа:

где 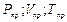— приведенные давление, объем и температура

Уравнение состояния газов Baн-дep-Ваальса наиболее точно определяет поведение легких газов при давлении до 100 атм и температуре 0-20 0 С. Применение этого уравнения к пропану и бутану или их смесям в назначенном диапазоне температур и давлений приводит к ошибкам, величина которых не превышает 10%.

Однако уравнение Ван-дер-Ваальса громоздко и пользоваться им при термодинамических расчетах трудно. Значительно удобнее и легче пользоваться уравнением состояния идеального газа, введя в него эмпирическую безразмерную поправку:

Безразмерный поправочный коэффициент z называется коэффициентом сжимаемости газов.

Эта эмпирическая величина, выражающая отклонение реальных газов от идеальных, находится из специальных графиков, построенных по приведенным температурам и давлениям.

Коэффициент сжимаемости в согласовании с законом соответствующих состояний связан с критическими и приведенными параметрами. Так как согласно уравнению (1.13)

,

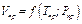
то можно записать

.

(1.15)

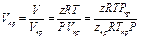
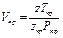
Если уравнение (1.15) написать в выражениях критических параметров, то получим значение критического коэффициента сжимаемости, т. е. значение коэффициента сжимаемости для критической точки

,

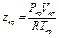
Для абсолютного большинства веществ значение Zкр лежит в пределах 0,25—0,29, а в среднем принимается равным около 0.265

Отклонение газов от законов газового состояния при нормальных условиях может быть определено по уравнению

,

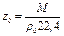
где ρ₀ — плотность при нормальных условиях, определенная экспериментально.

Зная коэффициент сжимаемости при нормальных условиях, можно определить его значение и при любых других условиях по уравнению:

.

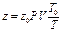
Процессы сжатия и расширения газа

Изменение состояния газа в зависимости от условий может происходить различно, причем каждый комплекс условий определяет соответствующий процесс изменения состоя­ния газа.

Изменение состояния газа может происходить без теплообмена с ок­ружающей средой (обычно это бывает при очень быстром течении процес­са, например при движении газа в сопле реактивного двигателя). Такой процесс называется адиабатным и характеризуется уравнением: рV к = const, откуда следуют такие соотношения:

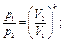
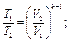
где k = c_p/c_w— показатель адиабаты; с_р — теплоемкость газа при р = const; c_w—теплоемкость газа при V= const.

Все перечисленные выше процессы являются частными случаями по-литропного процесса, при котором ни один параметр газа не остается неиз­менным и состояние газа изменяется в условиях теплообмена с окружаю­щей средой. Он характеризуется соотношением рV n = const, откуда следуют равенства:

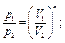
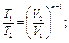
где п — показатель политропы.

При п = k — получим адиабатный процесс, при n = 1 — изотермический, при п = 0 — изобарный, при п = ∞- изохорный.

🎥 Видео