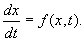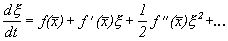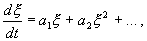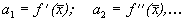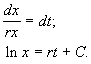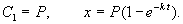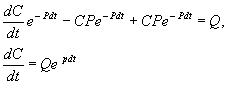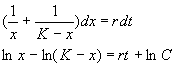Уравнение состояния линейных систем линеаризация уравнений состояния (8 видео)

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Содержание

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
Пример
2.3. Классический способ решения уравнений динамики
Пример
Уравнения состояния
Уравнение состояния линейных систем линеаризация уравнений состояния
💥 Видео

Видео:Устойчивость 1 ОпределениеСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

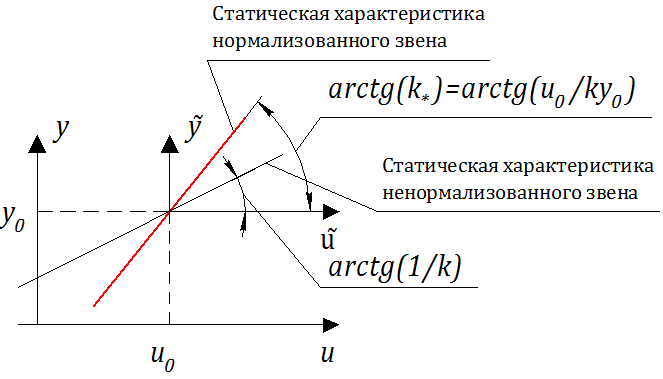
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

Нелинейностью статической характеристики.
Нелинейностью динамических членов в уравнениях динамики.
Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

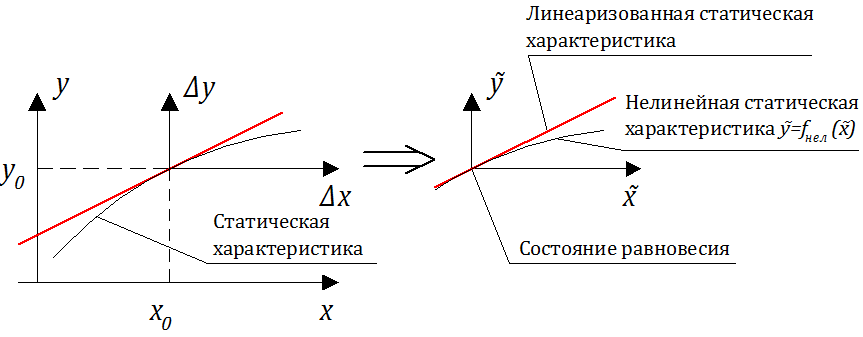
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

Перейдем к безразмерным переменным (нормализованным);
Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

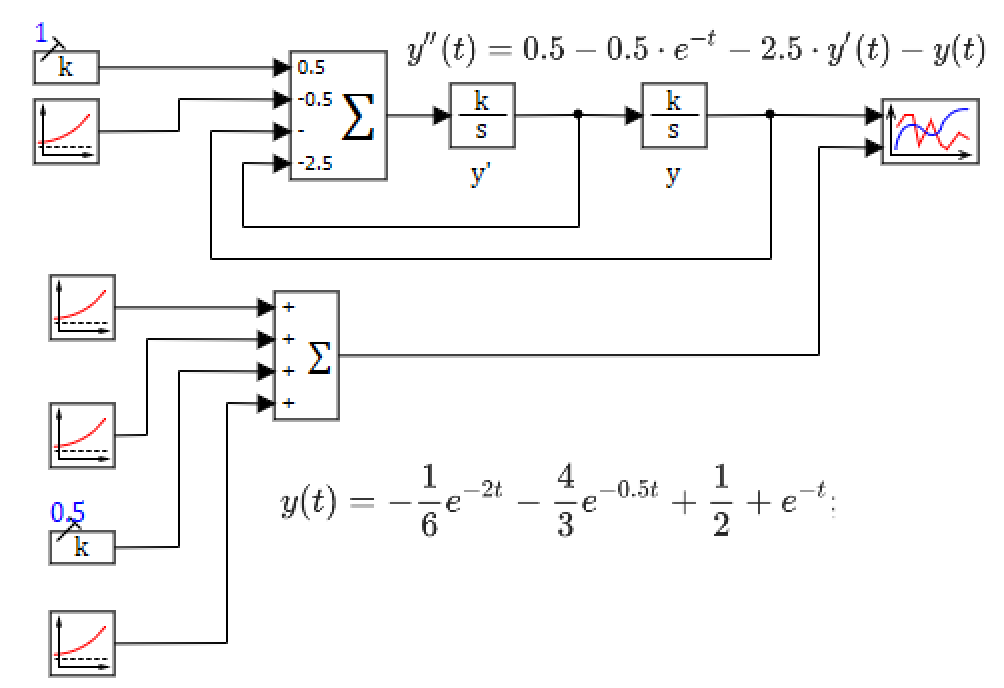
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Уравнения состояния

При решении некоторых задач теории автоматического управления удобнее представлять дифференциальное уравнение объекта (5.1) или дифференциальные уравнения системы (5.4) и (5.6) в виде совокупности дифференциальных уравнений первого порядка. Не умаляя общности, рассмотрим эти уравнения применительно к управляемому объекту.

Пусть объект описывается дифференциальным уравнением n-го порядка (5.1)

называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений

устанавливается алгебраическим уравнением

Обычно уравнения (5.71) и (5.72) записываются в векторпо-матричной форме:

— матрицы-столбцы. Матрицу-столбец-

могут иметь неодинаковые размерности.

В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений (5.73) и (5.74), т. е. вид входящих в них матриц.

При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина п- 1 ее производные:

т. с. когда оно имеет вид

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, хих2 и х:]) могут быть непосредственно измерены датчиками различных типов.

Для получения уравнений состояния в канонической форме уравнение объекта (5.70) представляется в виде

Если корни рь Ръ-Рп полинома С0(р) действительные однократные, то правая часть (5.80) может быть представлена в виде суммы элементарных дробей:

где К; и ()г- — коэффициенты разложения.

В качестве неременных состояния выбираются слагаемые суммы (5.81):

Большим достоинством канонической формы является диагоиальиость матрицы Л , что существенно упрощает решение уравнения (5.73). Основной недостаток ее состоит в том, что переменные состояния не имеют ясного физического смысла, в результате чего возникает проблема их непосредственного измерения.

Существуют и другие способы выбора переменных состояния, которые здесь не рассматриваются.

Решение векторно-матричиого уравнения (5.73) может быть представлено в виде

Здесь оно без строгого доказательства построено по аналогии с решением линейного дифференциального уравнения 1-го порядка

общий интеграл которого, как известно, определяется но формуле

называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда

При других формах уравнений состояния для определения фундаментальной матрицы можно использовать известные способы нахождения матричных функций, например, теоремы Кели—Гамильтона или Сильвестра. Можно также использовать формулу

—

При необходимости можно осуществить обратный переход от уравнений состояния к передаточным функциям объекта. Для этого уравнение (5.73) запишем в изображениях по Лапласу:

получается формула (5.88). Из уравнения

(5.74) с учетом (5.89) найдем изображение управляемой величины при нулевых начальных значениях:

При описании свойств объекта уравнениями состояния возникают две проблемы, нетипичные для случая, когда используется одно дифференциальное уравнение я-то порядка. Эти проблемы рассматриваются в следующем параграфе.

Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Уравнение состояния линейных систем линеаризация уравнений состояния

МОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ

ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА

Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост.

Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка:

Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид:

(2.1)

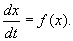
Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t.

Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)

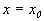
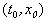
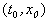
Пусть заданы начальные условия при t =0 или, иначе, пусть на плоскости t, x задана точка с координатами . Если для уравнения (2.1) выполнены условия теоремы Коши, то имеется единственное решение уравнения (2.1), удовлетворяющее этим начальным условиям, и через точку проходит одна единственная интегральная кривая x( t) .

Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

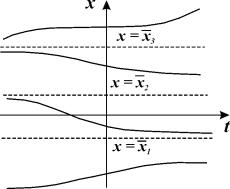
Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.

Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.

Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).

Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.

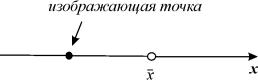
Стационарное состояние (точка покоя, особая точка, состояние равновесия)

В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:

(2.2)

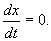
Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:

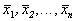
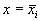
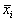
Корни алгебраического уравнения (2.3): суть стационарные состояния дифференциального уравнения (2.1). На плоскости ( t, x) прямые – асимптоты, к которым приближаются интегральные кривые. На фазовой прямой (рис. 2.2) стационарное состояние – точка, к которой стремится величина x.

Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.

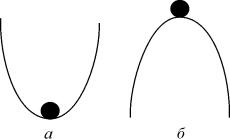
Рис. 2.3. К понятию устойчивости состояния равновесия

Устойчивость состояния равновесия

Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.

Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»

Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.

Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.

Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :

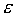
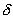
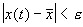
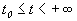
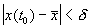
Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное , всегда можно найти такое , что

для если .

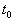
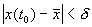
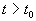
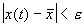
Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени отклонение от состояния равновесия мало ( ), то в любой последующий момент времени отклонение решения системы от состояния равновесия будет также мало: .

Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).

Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.

Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.

Устойчивое стационарное состояние представляет собой простейший тип аттрактора.

Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).

В нашем курсе мы рассмотрим следующие типы аттракторов:

· устойчивая точка покоя;

· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );

· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).

Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.

Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.

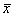
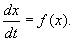
Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть — стационарное решение уравнения:

(2.1)

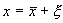
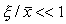
Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: , причем .

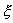
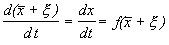
Перейдем в уравнении (2.1) от переменной x к переменной , т.е. новой переменной будет отклонение системы от стационарного состояния.

Учтем, что 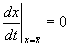по определению стационарного состояния.

Правую часть разложим в ряд Тейлора в точке :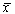

где

Отбросим члены порядка 2 и выше. Останется линейное уравнение:

(2.4)

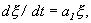
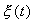
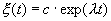
которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для находится сразу:

, (2.5)

где 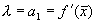, с — произвольная постоянная.

Если SYMBOL 108 f «Symbol» s 12 l SYMBOL 60 f «Symbol» s 12 0 , то при 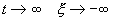и, следовательно, первоначальное отклонение SYMBOL 120 f «Symbol» s 12 x от состояния равновесия со временем затухает. Это означает, по определению, что состояние равновесия устойчиво.

Если же SYMBOL 108 f «Symbol» s 12 l SYMBOL 62 f «Symbol» s 12 > 0 , то при 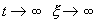, и исходное состояние равновесия неустойчиво.

Если SYMBOL 108 f «Symbol» s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.

Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.

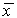
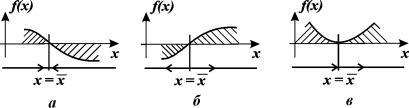
Итак, устойчивость стационарного состояния уравнения dx/dt=f(x) определяется знаком производной правой части в стационарной точке.

В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).

По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.

Здесь возможны три случая (рис. 2.4 а, б, в).

1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).

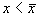
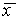
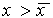
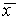
Отклоним изображающую точку системы в сторону . В этой области скорость изменения x dx/dt = f(x) положительна. Следовательно, x увеличивается, т.е. возвращается к . При скорость изменения величины x уменьшается, т.к. функция f(x) SYMBOL 60 f «Symbol» s 12 0. Следовательно, здесь x уменьшается и опять стремится к . Таким образом, отклонения от стационарного состояния в обе стороны затухают. Стационарное состояние устойчиво.

Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)

a – стационарное состояние 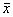устойчиво;

б, в ‑ стационарное состояние 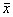неустойчиво

2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .

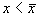
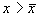
Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область . Теперь в область .

В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.

3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .

Поскольку 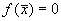, это означает, что изображающая точка, помещенная достаточно близко к состоянию равновесия с одной стороны, будет приближаться к нему, помещенная с другой стороны – удаляться.

Вопрос. Является ли состояние равновесия в случае 3 устойчивым?

Ответ. Нет. По определению устойчивости.

1. Рост колонии микроорганизмов

За время D t прирост численности равен:

где R – число родившихся и S – число умерших за время SYMBOL 68 f «Symbol» s 12 D t особей пропорциональные этому промежутку времени:

В дискретной форме:

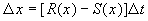
Разделив на SYMBOL 68 f «Symbol» s 12 D t и переходя к пределу при t SYMBOL 174 f «Symbol» s 12 ® 0 , получим дифференциальное уравнение

. (2.6)

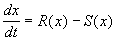
В простейшем случае, когда рождаемость и смертность пропорциональны численности:

(2.7)

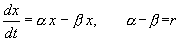
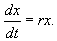
Разделим переменные и проинтегрируем:

Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.

(2.8)

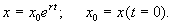
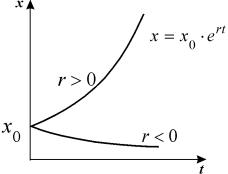
График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.

Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

2. Вещество переходит в раствор

Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: .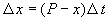

В форме дифференциального уравнения этот закон выглядит в

. (2.9)

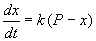
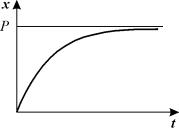
Разделим в этом уравнении переменные, и проинтегрируем:

(2.10)

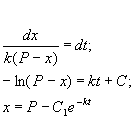
Здесь C ₁ — произвольная постоянная. Если x (0) = 0,

График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.

Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?

Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/

1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.

2. Линейные дифференциальные уравнения (не обязательно автономные).

3. Некоторые специальные виды уравнений.

Решение линейного уравнения

Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

. (2.11)

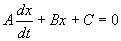
Здесь A, B, C — заданные непрерывные функции от t.

Пусть в некотором интервале изменения t A SYMBOL 185 f «Symbol» s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:

. (2.12)

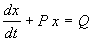
Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 f «Symbol» s 12 _ 0 – неоднородным.

Решим сначала однородное уравнение.

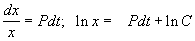
Общее решение линейного однородного уравнения имеет вид:

. (2.13)

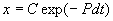
Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:

Теперь С находим интегрированием: 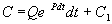. Здесь С₁ – произвольная постоянная.

Итак, общее решение линейного неоднородного уравнения первого порядка:

(2.14)

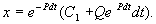
Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:

1) общее решение однородного уравнения (2.13) и

2) частное решение неоднородного уравнения, которое получается из общего решения, если С₁ = 0.

Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:

. (2.15)

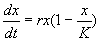
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .

Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:

. (2.16)

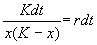
Представим левую часть в виде суммы и проинтегрируем

Переходя от логарифмов к переменным, получим:

(2.17)

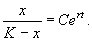
Здесь С – произвольная постоянная, которая определяется начальным значением численности x₀ :

; .

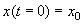
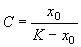
Подставим это значение С в формулу (2.17):

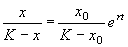
Отсюда получим решение – зависимость численности от времени:

. (2.18)

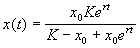
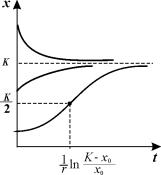
График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.

Рис.2.7. Динамика численности в логистической модели 2.18

при разных начальных значениях численности

Если начальное значение х₀ К/2, кривая роста имеет точку перегиба. Если х₀ > К, численность со временем убывает.

В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.

В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.