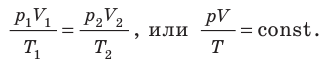Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.
ν — количество вещества [моль]
R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]
T – температура [K]
Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.
- Вывод уравнения Менделеева-Клапейрона
- Закон Бойля-Мариотта — изотермический процесс
- Закон Гей-Люссака — изобарный процесс
- Закон Шарля — изобарный процесс
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение состояния идеального газа
- Уравнение состояния идеального газа
- Уравнение Менделеева-Клапейрона
- Уравнение состояния для смеси газов
- Что мы узнали?
- 🔥 Видео
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Вывод уравнения Менделеева-Клапейрона
Давление идеального газа зависит от концентрации частиц и температуры тела:
n — концентрация частиц [м -3 ]
k – константа Больцмана k = 1,38 · 10 -23 [Дж/К]
Т – абсолютная температура, в кельвинах [К]
Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:
Подставим nkT вместо давления и выразим кинетическую энергию:
Концентрация частиц газа n равна:
N – число молекул газа в емкости объемом V [м 3 ]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:
Подставим эти величины в уравнение давления идеального газа (p=nkT):
Произведение числа Авогадро NA и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:
Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:
можно привести уравнение к следующему виду:
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.
Закон Бойля-Мариотта — изотермический процесс
Проходит при постоянной температуре: T= const.
P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:
Закон Гей-Люссака — изобарный процесс
Проходит при постоянном давлении: P = const.
V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:
Закон Шарля — изобарный процесс
Проходит при постоянном объеме: V = const.
P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:
Понравилась статья, расскажите о ней друзьям:
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 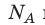
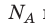
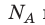
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (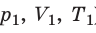
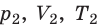
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 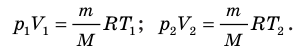
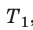
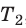
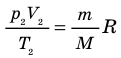
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (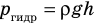
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (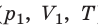
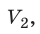
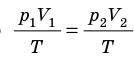
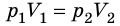
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 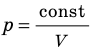
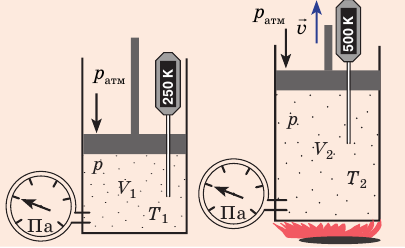
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (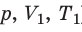
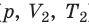
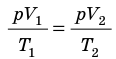
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (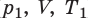
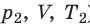
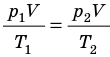
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 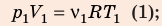

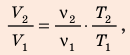
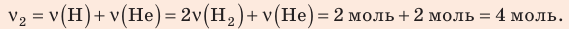
Ответ: примерно в 2,7 раза.
Пример №2
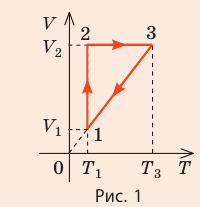
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
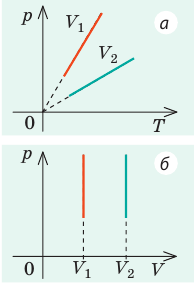
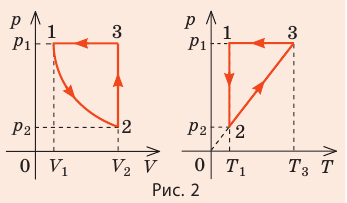
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнение состояния идеального газа

Средняя оценка: 4.5
Всего получено оценок: 87.
Средняя оценка: 4.5
Всего получено оценок: 87.
Идеальный газ – это теоретическая модель газа, хорошо описывающая поведение реальных газов при невысоких давлениях и температурах. Для описания его макроскопических параметров (температуры, давления и объема) используется специальное соотношение, называемое уравнением состояния. Рассмотрим его подробнее.
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Уравнение состояния идеального газа
Основное уравнение состояния идеального газа выводится на основе положений молекулярно-кинетической теории. Согласно этой теории, идеальный газ – это вещество в газообразном состоянии, для которого справедливы следующие допущения:
- молекулы представляют собой материальные точки;
- силы взаимного притяжения молекул отсутствуют;
- молекулы движутся хаотично, при этом каждая движется в соответствии с законами механики Ньютона;
- взаимодействия между молекулами состоят только в абсолютно упругих соударениях.
Согласно основному уравнению молекулярно-кинетической теории, если концентрация молекул газа (количество в единице объема) равно $n$, масса одной молекулы $m_0$, а ее среднеквадратичная скорость $overline $, то давление такого газа равно:
Поскольку молекулы газа считаются материальными точками, то средняя кинетическая энергия движущейся молекулы равна:
Выразим из этого соотношения массу молекулы, и подставим в предыдущее. Получим:
Средняя энергия молекулы в молекулярно-кинетической теории связана с температурой газа через постоянную Больцмана ($k=1,38×10^Дж/К$):
Подставив эту среднюю энергию в предыдущее выражение, получим:
Наконец, выразим концентрацию молекул как отношение их количества к объему ($n=$). В итоге получим:
Данное соотношение было впервые получено и практически доказано в 1834г. Б. Клапейроном, поэтому оно носит название «уравнение Клапейрона».
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение Менделеева-Клапейрона
Уравнение Клапейрона хорошо описывает изменение в газовых процессах макроскопических параметров некоторого количества газа. Однако, заранее сказать, какими будут эти параметры для конкретной массы некоторого конкретного газа, нельзя. Константа, присутствующая в уравнении Клапейрона должна вычисляться каждый раз заново.
В 1874 г Д. Менделеев сделал вывод, что эта константа прямо пропорциональная количеству вещества газа, то есть отношению общей массы газа $m$ к его молярной массе $М$:

А поскольку один моль любого газа в одинаковых условиях занимает один и тот же объем, можно ввести специальный коэффициент, $R=8.31 $. С этим коэффициентом уравнение состояния идеального газа получит вид:
Значение температуры чаще всего переносят в правую часть формулы. Окончательно имеем:
Уравнение состояния идеального газа в таком виде называется уравнением Менделеева-Клапейрона. Данное уравнение связывает макроскопические параметры газа с его физическими параметрами.
Постоянная R, присутствующая в уравнении, называется универсальной газовой постоянной. Она равна произведению числа Авогадро на постоянную Больцмана, и представляет количество тепла, которое необходимо сообщить одному молю газа для увеличения его температуры на один кельвин.
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение состояния для смеси газов
Уравнение состояния идеального газа описывает макроскопические параметры конкретного газа. Однако, в задачах нередко необходимо определять параметры смеси газов с разными молярными массами.
В этом случае применяется закон Дальтона.

Давление для каждой из компонент газа вычисляется отдельно, как если бы эта компонента была бы одна. Такое давление называется парциальным, а потом, общее давление смеси, в соответствии с законом Дальтона находится, как сумма парциальных давлений всех компонент.
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Что мы узнали?
Уравнение состояния идеального газа связывает объем, давление и температуру (макроскопические газовые параметры) с общей и молярной массой газа. Данное уравнение называется уравнением Менделеева-Клапейрона. Для расчета параметров смеси газов используется закон Дальтона.
🔥 Видео
идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Уравнение состояния идеального газаСкачать

Уравнение состояния идеального газаСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать

Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Температура. Вывод уравнения состояния идеального газа на основе МКТСкачать

ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

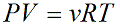
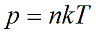
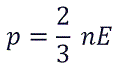
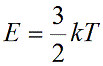
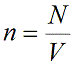
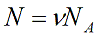
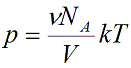
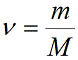
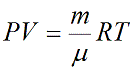

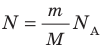
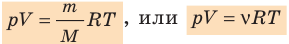
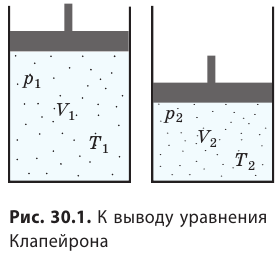
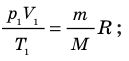
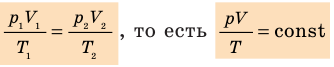
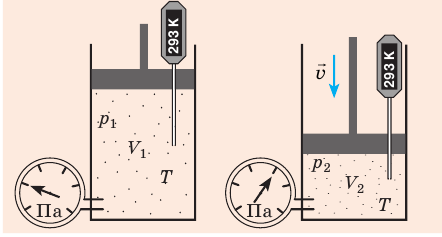
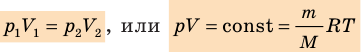
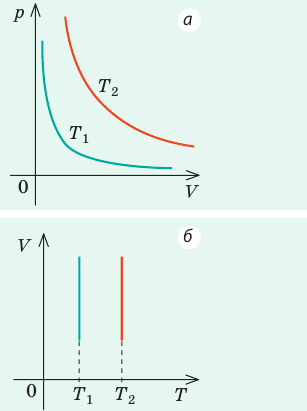

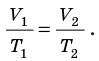
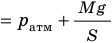
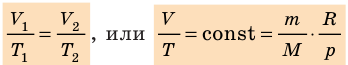
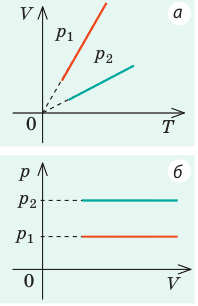

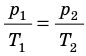
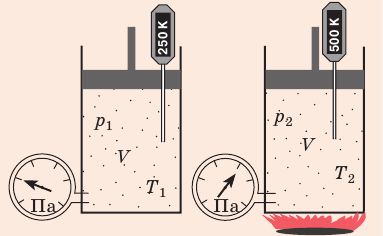
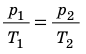
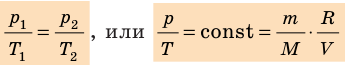

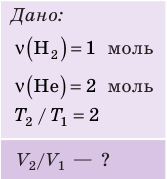
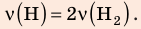

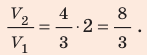
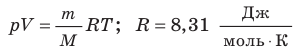 — универсальная газовая постоянная.
— универсальная газовая постоянная.