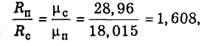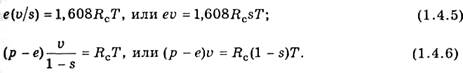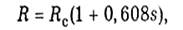Уравнение состояния газов в метеорологии (5 видео)

Содержание

Плотность воздуха. Уравнение состояния газов
Уравнение состояния газов
Уравнение состояния влажного воздуха
💡 Видео

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Плотность воздуха. Уравнение состояния газов

Основными характеристиками физического состояния любого газа является плотность, давление и температура. Между этими характеристиками существует связь, которая для идеальных газов выражается уравнением состояния газов

где Р – давление;
V – удельный объем газа V = 1 / ρ.
Т – температура по абсолютной шкале;
R – газовая постоянная;
ρ – плотность газа.

Применяя уравнение состояния газов к сухому воздуху и вводя числовое значение газовой постоянной для сухого воздуха R = 2,87·10 6 см 2 /сек 2 ·град можно получить выражение для плотности сухого воздуха.

Один кубический метр воздуха при t° = 4°С и нормальном давлении имеет массу 1,293 кг. Следовательно, при данных условиях плотность воздуха 1,293 кг/м куб. Это примерно в 800 раз меньше плотности воды.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение состояния газов

Основными характеристиками физического состояния газа являются его давление, температура и плотность. Все эти величины взаимозависимы. Газы сжимаемы, поэтому их плотность меняется в зависимости от давления и температуры. Связь между давлением, температурой и плотностью для идеальных газов дается уравнением состояния газов, известным из физики. Оно пишется

, (1)

где – давление; — удельный объем газа; — температура по шкале Кельвина;

— удельная газовая постоянная, зависящая от природы газа.

Для каждого газа существует температура, называемая критической, выше которой любой газ можно с большой степенью точности назвать идеальным. Если температура газа выше критической, то газ ни при каком давлении не может быть переведен ни в жидкое, ни в твердое состояние.

Идеальный газ, находясь в смеси с другими газами, ведет себя независимо от них, имея собственные давление плотность , удельный объем . В случае термодинамического равновесия смеси у всех газов должна быть общая температура Т. Общее давление газа, согласно закону Дальтона, должно равняться сумме их парциальных давлений.

Рассмотрим уравнение состояния газа применительно к сухому воздуху, поскольку он как смесь газов удовлетворяет изложенным выше положениям физики. В табл. 2 приведены значения критической температуры для основных газов, входящих в состав сухого воздуха.

Критическая температура газов, входящих в состав сухой атмосферы

Для сухого воздуха, кроме входящего в него углекислого газа, все газы имеют критическую температуру более низкую, чем температуры, наблюдаемые в земной атмосфере, т.е. сухой воздух можно считать смесью идеальных газов. Углекислый газ в атмосфере имеет очень малое парциальное давление, далекое от насыщающего, т.е. в естественных условиях он также не может сконденсироваться.

Для каждого газа, входящего в атмосферу, можно записать уравнение состояния

, (2)

где – парциальное давление, — удельный объем, – удельная газовая постоянная для соответствующего газа, входящего в смесь.

Удельная газовая постоянная связана с универсальной R= 8,31441·103 Дж/кмоль·К так:

, (3)

где – относительная молекулярная масса газа.

Общее давление смеси

. (4)

Принимая массу сухого воздуха равной единице, а массу газа , имеем

, (5)

где: – удельный объем сухого воздуха

Используя уравнения (1), (4) и (5), запишем

(6)

, (7)

где – удельная газовая постоянная сухого воздуха. Она представляет собой результирующую вклада каждой компоненты смеси пропорционально удельной газовой постоянной и относительной массы в смеси каждого газа

. (8)

Относительная молекулярная масса сухого воздуха при известном по углеродной шкале получается на основе универсальной газовой постоянной

= 28,97 кг/моль. (9)

Рассмотрим влажный воздух как смесь сухого воздуха и водяного пара. Поскольку критическая температура водяного пара равна 374ºС, он как примесь идеального газа к смеси газов, формирующих сухой воздух, рассматриваться не может. Условие, когда фактическая температура меньше критической, является необходимым, но недостаточным для перехода газа в жидкость или твердое состояние. Необходимо также, чтобы его парциальное давление достигло состояния насыщения. Последнее является только функцией температуры, свойств газа и формы поверхности, для которой она рассчитывается. Здесь будет рассмотрен водяной пар, который до момента насыщения можно считать примесью идеального газа.

Уравнение состояния водяного пара можно представить в следующем виде:

, (10)

где — парциальное давление, – удельный объем, – удельная газовая постоянная водяного пара.

= 461,5 Дж/кг·К, (11)

где = 18,015 кг/моль – относительная молекулярная масса водяного пара.

Как показывают экспериментальные исследования и расчеты, в диапазоне температур от 0 до 40ºС удельная постоянная водяного пара практически совпадает с теоретической и не меняется.

Для вывода уравнения состояния рассмотрим 1 кг влажного воздуха. В нем содержится q кг водяного пара и кг сухого воздуха. Обозначим через и удельные объемы водяного пара, сухого и влажного воздуха.

Сухой воздух и водяной пар равномерно распределены по объему влажного воздуха и полностью его занимают. Удельные объемы водяного пара и сухого воздуха соответственно равны

и . (12)

Если обозначить — общее давление, —общую температуру, – парциальное давление сухого воздуха, то уравнение состояния сухой части воздуха имеет вид

. (13)

Отношение удельных газовых постоянных водяного пара и сухого воздуха

= 1,608 (14)

Заменив удельную газовую постоянную водяного пара удельной газовой постоянной сухого воздуха с соответствующим коэффициентом, получим уравнение состояния влажного воздуха

Множитель (1 + 0,608q) в метеорологии относят к температуре, вводя понятие виртуальной температуры

Она всегда не меньше молекулярной, так как влажность может меняться от 0 до насыщающей.

Таким образом, виртуальная температура – это температура, которую должен иметь сухой воздух, чтобы его плотность при том же давлении была равна плотности влажного воздуха.

Плотность влажного воздуха всегда меньше плотности сухого. В некоторых случаях это может служить дополнительным фактором, способствующим развитию свободной конвекции в атмосфере.

Плотность воздуха в каждом месте непрерывно меняется во времени. Кроме того, она сильно меняется с высотой, потому что с высотой меняются также атмосферное давление и температура воздуха. Давление с высотой всегда уменьшается, а вместе с ним убывает и плотность. Температура с высотой по большей части понижается, по крайней мере в нижних 10-15 кматмосферы. Но падение температуры влечет за собой повышение плотности. В результате совместного влияния изменения давления и температуры плотность с высотой, как правило, понижается, но не так сильно, как давление. В среднем для Европы она равна у земной поверхности 1250 г/м3, на высоте 5 км – 735 г/м3, 10 км – 411 г/м3, 20 км – 87 г/м3.

На высотах около 300 кмплотность воздуха имеет порядок величины 10-8 г/м3, т.е. в сто миллиардов раз меньше, чем у земной поверхности. На высоте 500 км плотность воздуха уже 10-9 г/м3,на высоте 750 км – 10-10 г/м3или еще меньше. Эти значения плотности ничтожны по сравнению с приземными. Но все же до высот более 20 тыс. кмплотность воздуха остается значительно большей, чем плотность вещества в межпланетном пространстве.

Если бы плотность воздуха не менялась с высотой, а оставалась на всех уровнях такой же, как у земной поверхности, то для высоты атмосферы получилась бы величина около 8000 м.В самом деле, приземная плотность сухого воздуха при давлении 760 мми температуре 0° равна 1293 г/м3;столб воздуха с этой плотностью должен был бы иметь высоту, очень близкую к 8000 м,чтобы производить такое же давление, какое производит столб ртути в 760 мм высотой (1033 г/см3).Указанная высота (8000 м)называется высотой однородной атмосферы. В действительности плотность воздуха с высотой убывает, и потому истинная высота атмосферы равняется многим тысячам километров.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение состояния влажного воздуха

Влажный воздух представляет собой механическую смесь сухого воздуха и водяного пара. Поскольку критическая температура водяного пара (Т_кр =374 °С) выше наблюдаемых в атмосфере температур, то он в реальных условиях атмосферы может переходить в жидкое и твердое состояния (конденсироваться).

Теория фазовых переходов водяного пара детально рассматривается в разделе IV. Здесь отметим только, что условие Т

Примем следующие обозначения: р — общее давление; Т — температура, одинаковая для водяного пара, сухого и влажного воздуха; е — парциальное давление водяного пара; (р — е) — парциальное давление сухого воздуха. Уравнением состояния водяного пара служит уравнение (1.4.1). Уравнение состояния сухой части воздуха имеет вид

Подставим в уравнения (1.4.1) и (1.4.3) значения удельных объемов в соответствии с (1.4.2) и удельной газовой постоянной водяного пара в соответствии с (1.4.4):

Сложив уравнения (1.4.5) и (1.4.6), получим уравнение состояния влажного воздуха:

которому можно придать два различных вида в зависимости от того, отнесен ли множитель (1 + 0,608s) к удельной газовой постоянной Rc или к температуре Т.

Если ввести удельную газовую постоянную влажного воздуха

то уравнение (1.4.7) примет вид

Удельная газовая постоянная R в этом уравнении — величина переменная, зависящая от влажности воздуха s.

В метеорологии множитель (1 + 0,608s) обычно относят к температуре, вводя понятие виртуальной температуры

Нередко виртуальную температуру представляют в виде суммы:

где ∆T_v — виртуальный добавок. Из сравнения последнего выражения с (1.4.9) следует:

Если водяной пар находится в состоянии насыщения, то ∆T_v при данных Т и р достигает наибольшего значения

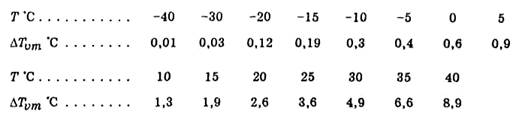
которое при фиксированном р является функцией одной лишь температуры. При р = 1000 гПа максимальный виртуальный добавок ∆T_v_т имеет следующие значения:

Из этих данных вытекает, что виртуальный добавок, а соответственно и роль влажности в изменении плотности воздуха малы при низких температурах и достаточно велики при высоких.

С введением виртуальной температуры уравнение состояния влажного воздуха принимает вид

Если в (1.4.11) ввести плотность влажного воздуха p = l/v, то уравнение состояния влажного воздуха примет вид

Из сравнения уравнения (1.4.12) с уравнением (1.3.8) следует, что при одинаковых температуре и давлении плотность влажного воздуха всегда меньше плотности сухого воздуха. Физически это объясняется тем, что в состав влажного воздуха входит более легкий по сравнению с сухим воздухом водяной пар, который вытесняет часть сухого воздуха.