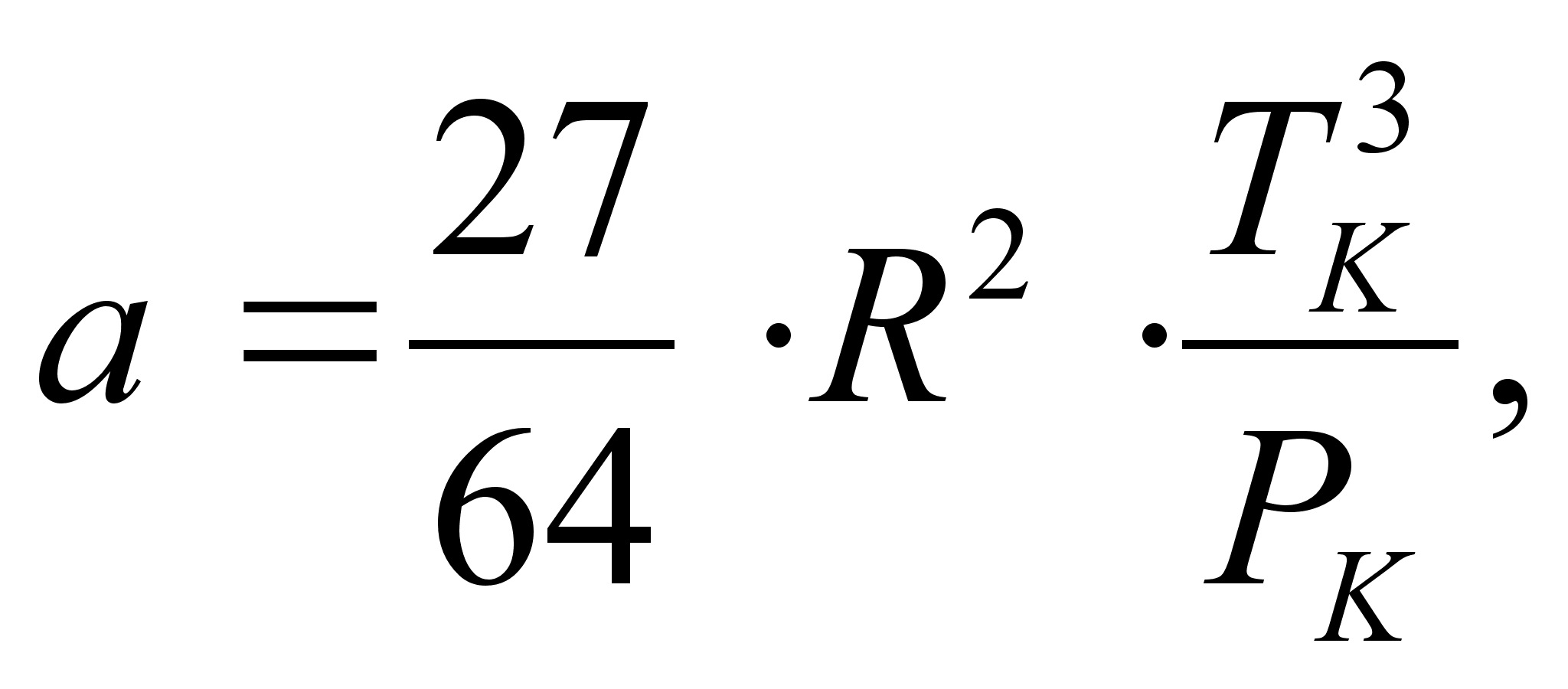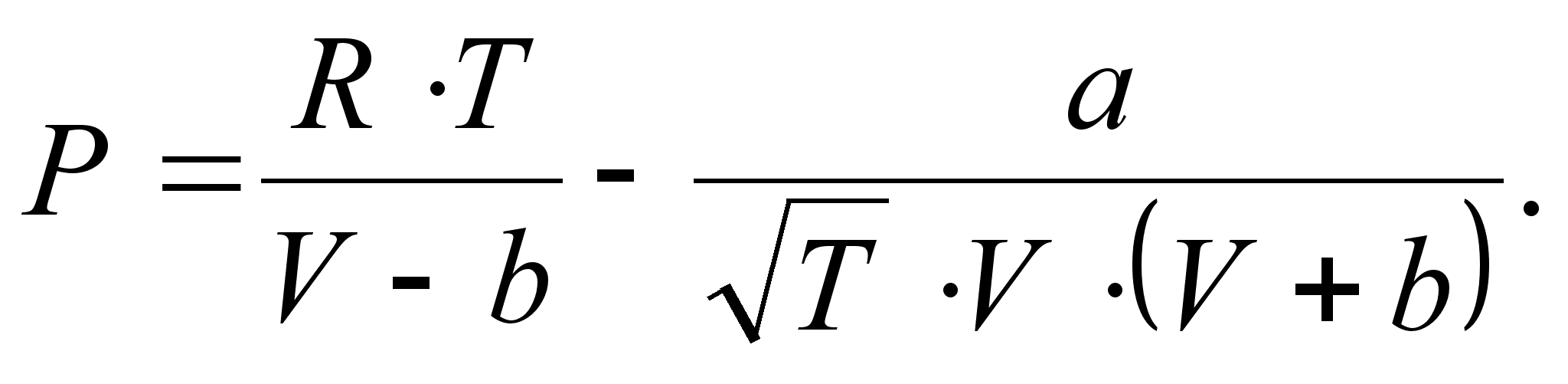| Название: Идеальный газ 2 Раздел: Рефераты по физике Тип: реферат Добавлен 14:24:43 06 июля 2011 Похожие работы Просмотров: 3610 Комментариев: 23 Оценило: 17 человек Средний балл: 4.4 Оценка: 4 Скачать | ||
 |
температурах.
Закон Бойля — Мариотта следует из кинетической теории газов, когда принимается допущение, что размеры молекул пренебрежимо малы по сравнению с расстоянием между ними и отсутствует межмолекулярное взаимодействие. При больших давлениях необходимо вводить поправки на силы притяжения между молекулами и на объем самих молекул. Как и уравнение Клайперона, закон Бойля — Мариотта описывает предельный случай поведения реального газа, более точно описываемый уравнением Ван-дер-Ваальса. Применение закона приближенно можно наблюдать в процессе сжатия воздуха компрессором или в результате расширения газа под поршнем насоса при откачке его из сосуда.
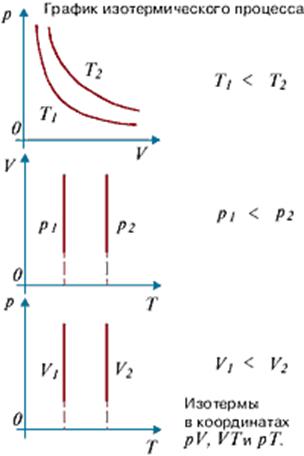
Термодинамический процесс, котроый происходит при постоянной температуре называется изотермическим. Изображение его на графике называется изотермой.(см. график изотермического процесса)
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Закон Гей-Люссака. Изобара
Французский ученый Ж. Гей-Люссак в 1802 году нашел экспериментально зависимость объема газа от температуры при постоянном давлении. Данные лежат в основе газового закона Гей-Люссака.
Формулировка закона Гей-Люссака следующая: для данной массы газа отношение объема газа к его температуре постоянно, если давление газа не меняется. Эту зависимость математически записывают так:
Данный закон приближенно можно наблюдать, когда происходит расширение газа при его нагревании в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня. Другим проявлением закона Гей-Люссака в действии является аэростат. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
Закон справедлив для идеального газа. Он неплохо выполняется для разреженных газов, которые по своим свойствам близки к
 |
идеальному. Температура газа должна быть достаточно велика.
Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0 . Эту прямую называют изобарой . Разным давлениям соответствуют разные изобары. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным . От греческого слова «барос» — вес (тяжесть). (см. график изобарного процесса).
Видео:Уравнение состояния идеального газаСкачать

Закон Шарля. Изохора
Французский ученый Ж. Шарль в 1787 году нашел экспериментально зависимость давления газа от температуры при постоянном объеме. Данные лежат в основе газового закона Шарля.
Формулировка закона Шарля следующая: для данной массы газа отношение давления газа к его температуре постоянно, если объем газа не меняется. Эту зависимость математически записывают так:
 |
P /Т= const , если V = const и m = const
Данный закон приближенно можно наблюдать, когда происходит увеличение давления газа в любой емкости или в электрической лампочке при нагревании. Изохорный процесс используется в газовых термометрах постоянного объема. Закон Шарля не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
Закон справедлив для идеального газа. Он неплохо выполняется для разреженных газов, которые по своим свойствам близки к идеальному. Температура газа должна быть достаточно высокой. Процесс должен проходить очень медленно
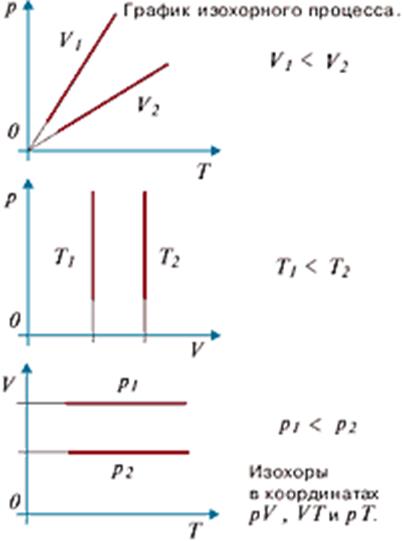
Графически эта зависимость в координатах P-T изображается в виде прямой, выходящей из точки Т=0 . Эту прямую называют изохорой . Разным объемам соответствуют разные изохоры. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным . От греческого слова «хорема»-вместимость. (см. графики изохорного процесса
Видео:идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Заключение
Газовые законы — законы термодинамических процессов, протекающих в системе с неизменным количеством вещества при постоянном значении одного из параметров: закон Шарля, закон Гей-Люссака, закон Бойля-Мариотта, а также закон Авогадро, закон Дальтона.
Видео:Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Список источников
1. Вукалович М.П., Новиков И.И. — Термодинамика. М: Машиностроение, 1972
2. Грабовский Р.И. Курс физики. М: Высшая школа, 1974
3. Громов С. В., Физика: Оптика. Тепловые явления. Строение и свойства вещества: Учебник для 10 класса., Москва, «Просвещение», 2003 г.
4. Коротков П.Ф. Молекулярная физика и термодинамика — 2e изд., MФТИ, 2004
5. Мякишев Г. Я., Буховцев Б. Б., Сотский Н. Н., Физика, учебник для 10 класса общеобразовательных учреждений, Москва, «Просвещение», 2008г.
6. Якунин В. И., Учебное пособие для изучающих физику в средней школе., Тамбов, ТИПКРО, Тамбовский областной физико-математический лицей, 1994
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Реферат по физике на тему: «Понятие идеального и реального газа. Газовые законы»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Реферат по физике на тему: « Понятие идеального и реального газа. Газовые законы »
Характеристика идеального и реального газов…………………………………………. 3
Основное уравнение кинетической теории газа…………………………………………..7
Список использованной литературы……………………………………………………………..13
Газы – агрегатное состояние вещества, в котором его частицы не связаны или весьма слабо связаны силами взаимодействия и движутся свободно, заполняя весь предоставленный им объём. Вещество в газообразном состоянии широко распространено в природе. Газы образуют атмосферу Земли, в значительных количествах содержатся в твёрдых земных породах, растворены в воде океанов, морей и рек. Солнце, звёзды, облака межзвёздного вещества состоят из газов – нейтральных или ионизованных. Встречающиеся в природных условиях газы представляют собой, как правило, смеси химически индивидуальных газов. Газы обладают рядом характерных свойств. Они полностью заполняют сосуд, в котором находятся, и принимают его форму. В отличие от твёрдых тел и жидкостей, объём газа существенно зависит от давления и температуры. Коэффициент объёмного расширения газа в обычных условиях (0-100°С) на два порядка выше, чем у жидкостей, и составляет в среднем 0,003663 град-1.
Газовые законы — законы термодинамических процессов, протекающих в системе с неизменным количеством вещества при постоянном значении одного из параметров: закон Шарля, закон Гей-Люссака, закон Бойля-Мариотта, а также закон Авогадро, закон Дальтона.
Характеристика идеального и реального газов
Идеальный газ – математическая модель газа , в которой в рамках молекулярно-кинетической теории предполагается, что:
потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией ;
суммарный объём частиц газа пренебрежимо мал;
между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги ;
время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями.[4]
В расширенной модели идеального газа, частицы, из которых он состоит, имеют форму упругих сфер или эллипсоидов , что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц. В рамках термодинамики идеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона-Менделеева .
Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики . Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса , в котором учитывается притяжение между молекулами.
Различают классический идеальный газ и квантовый идеальный газ.
Классический идеальный газ. Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
объём частицы газа равен нулю (то есть диаметр молекулы d пренебрежимо мал по сравнению со средним расстоянием между ними, ;
импульс передается только при соударениях (то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях);
суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучением)
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия – сумме энергий частиц газа. Свойства идеального газа описываются уравнением Менделеева — Клапейрона :
Равновесное распределение частиц классического идеального газа по состояниям описывается распределением Больцмана :
где – среднее число частиц, находящихся в j -ом состоянии с энергией , а константа a определяется условием нормировки:
где N – полное число частиц.
Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми-Дирака и Бозе-Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа . Для любого идеального газа справедливо соотношение Майера :
где R — универсальная газовая постоянная , — молярная теплоемкость при постоянном давлении, молярная теплоемкость при постоянном объёме.
Квантовый идеальный газ. Понижение температуры и увеличение плотности газа может привести к ситуации, когда среднее расстояние между частицами становится соизмеримым с длинной волны де Бройля для этих частиц, что приводит к переходу от классического к квантовому идеальному газу. В таком случае поведение газа зависит от спина частиц: в случае полуцелого спина ( фермионы ) действует статистика Ферми-Дирака ( Ферми-газ ), в случае целого спина ( бозоны ) – статистика Бозе-Эйнштейна ( Бозе-газ ).
Ферми-газ . Для фермионов действует принцип Паули , запрещающий двум тождественным фермионам находиться в одном квантовом состоянии. Вследствие этого при абсолютном нуле температуры импульсы частиц и, соответственно, давление и плотность энергии Ферми-газа отличны от нуля и пропорциональны числу частиц в единице объёма. Существует верхний предел энергии, который могут иметь частицы Ферми-газа при абсолютном нуле ( Энергия Ферми ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом .
Особенностью Ферми-газов является крайне слабая зависимость давления от температуры: в нерелятивистском случае давление , в релятивистском – .
Бозе-газ . Так как на бозоны принцип Паули не распространяется, то при снижении температуры Бозе-газа ниже некоторой температуры возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе-Эйнштейна . Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при давление Бозе-газа зависит только от температуры.
Примерами Бозе-газов являются различного рода газы квазичастиц (слабых возбуждений) в твёрдых телах и жидкостях , сверхтекучая компонента гелия II, конденсата Бозе-Эйнштейна куперовских электронных пар при сверхпроводимости . Примером ультрарелятивистского Бозе-газа является фотонный газ .[2]
Реальный газ – это газ , свойства которого существенно зависят от взаимодействия молекул.
В обычных условиях, когда средняя потенциальная энергия взаимодействия молекул много меньше их средней кинетической энергии, свойства реальных газов незначительно отличаются от свойств идеального газа и к реальным газам применимы законы, установленные для идеального газа. Отличие свойств реального газа от свойств идеального становится особенно значительным при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.
В модели идеального газа не учитывается собственный объем молекул и силы межмолекулярного взаимодействия. Тщательная экспериментальная проверка газовых законов современными методами показала, что эти законы достаточно точно описывают поведение реальных газов при небольших давлениях и высоких температурах. При других условиях наблюдаются значительные отступления от этих законов. Причина заключается в том, что, во-первых, при очень сильном сжатии газов объем незанятого молекулами пространства становится сравним с объемом, занимаемым самими молекулами; а во-вторых, при низких температурах становится заметным взаимодействие между молекулами. Поэтому для описания поведения газа при достаточно больших плотностях уравнения состояния идеального газа не пригодны. Наличие сил межмолекулярного взаимодействия, а именно сил отталкивания, действующих на малых расстояниях порядка размеров молекул, и сил притяжения, приводит к сложной зависимости энергии потенциального взаимодействия молекул от расстояния.
Для описания термодинамических свойств реальных газов используются различные уравнения состояния . При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа:
где p – давление, v – мольный объем, Т – абсолютная температура, R – газовая постоянная, В(Т), С(Т) и т. д. – вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и т. д. взаимодействия частиц в газе. Качественно верно описывает основные отличия реального газа от идеального уравнение Ван-дер-Ваальса , учитывающее существование сил притяжения между молекулами, действие которых приводит к уменьшению давления газа, и сил отталкивания, препятствующих безграничному сжатию газа.
Кроме уравнения Ван-дер-Ваальса было предложено много других эмпирических уравнений состояния реальных газов. Некоторые из них дают лучшее согласие с опытом за счет большого числа входящих в них феноменологических постоянных. Однако при качественном исследовании поведения реальных газов использование уравнения Ван-дер-Ваальса более удобно, благодаря его простоте и понятному физическому смыслу.
Одной из основных характеристик реальных газов являются размеры молекул. В реальных газах их называют газокинетическими радиусами, и их размер связан с характерными расстояниями, на которых проявляются силы межатомных и межмолекулярных взаимодействий.
В реальных газах возникают неоднородности полей давления и температуры, а также макроскопические потоки, которые приводят к переносу массы – диффузии. Для реальных газов характерна теплопроводность и вязкость. Главная особенность кинетических процессов переноса в реальных газах (в отличие от жидкостей и твердых тел) – наличие механизма столкновения молекул. Поэтому основной характеристикой этих процессов в газах является длина свободного пробега.
Внутренняя энергия реального газа зависит от объема V , то есть от расстояния между молекулами, так как потенциальная энергия молекул определяется их взаимным расположением.
Существование межмолекулярного взаимодействия в той или иной степени сказывается на всех свойствах реальных газов.[5]
Основное уравнение кинетической теории газа
Величина, измеряемая силой, действующей перпендикулярно на единицу площади поверхности тела, называется давлением.
Согласно определению, давлении . Ниже приводятся единицы давления и соотношения между ними:
1 н/м2, 1 атм, 1 ат, 1 мм рт. ст.
1 атм = 760 мм рт. ст. = 1,01*105 н/м2.
1 ат = 9,81*104 н/м2.
1 мм рт. ст. = 133 н/м2.
Давление газа на стенки сосуда – это сила, действующая перпендикулярно на единицу площади последнего. Причиной давления являются удары молекул о стенки сосуда. Сила удара одной молекулы пренебрежительно мала, но большое число ударов огромного количества молекул создает заметное давление газа на стенки сосуда. Выведем упрощенно формулу, по которой вычисляется давление идеального газа на стенки сосуда.
Допустим, что имеется прямоугольный цилиндр с поршнем, который может двигаться без трения (рис. 1).
Рис. 1. К выводу основного уравнения кинетической теории газов.
Давление газа на поршень . Найдем общую силу удара F молекул о поршень. Для этого первоначально по второму закону Ньютона найдем силу одного удара одной молекулы о поршень: F1 = Ma , где М – масса поршня, а – ускорение, с которым будет двигаться поршень. Умножив силу F1 на число молекул, движущихся вдоль оси Y , найдем общую силу удара молекул о поршень.
Пусть на покоящийся поршень летит перпендикулярно к нему молекула с массой m и скоростью v. За время продолжительности удара t скорость поршня изменится от v0 = 0 до v1 , и он получает ускорение
Так как поршень движется очень медленно, а молекула очень быстро, то можно некоторое время пренебрегать увеличением расстояния t и считать что удары молекулы о поршень следуют друг за другом через равные промежутки времени в течение которого происходит изменение скорости v1 .
До удара молекулы сумма импульсов ее и поршня равна mv . Удар молекулы о поршень вполне упругий, поэтому после удара она будет иметь импульс – mv , а поршень Mv1 . Сумма их импульсов: -mv + Mv1 . По закону сохранения импульса mv = -mv + Mv1 или 2mv = Mv1 .
Отсюда скорость, которую получил поршень, C каждым новым ударом молекулы поршень через равные промежутки времени t будет увеличивать свою скорость на величину 2mv/M . Тогда ускорение поршня:
Сила одного удара молекулы о поршень:
Ввиду хаотичности движения молекул по всем трем направлениям осей координат движется одинаковое количество молекул. Из общего числа n всех молекул 1/3 двигалась прямолинейно между поршнем и противоположной ему стенкой, 1/3 молекул – между верхней и нижней стенками и 1/3 – между дальней и ближней стенками. Все три направления одинаково вероятны.
Тогда сила давления молекул на поршень:
Давление газа на поршень:
где lS = V – объем газа.
Здесь – число молекул в единице объема газа. Следовательно :
где v — средняя квадратичная скорость.
Эта формула называется основным уравнением кинетической теории идеального газа для давления. Давление газа равно 1/3 произведения массы молекулы, числа молекул в единице объема и квадрату средней квадратичной скорости молекулы газа.[1]
Законы идеальных газов
Газы, подчиняющиеся законам Бойля-Мариотта, Гей-Люссака, Авогадро и Дальтона, называются идеальными. Эти законы и соотношения, построенные на их основе, можно применять также к реальным газам при сравнительно невысоких давлениях и сравнительно высоких температурах.
С молекулярно-кинетической точки зрения идеальный газ – это газ, в котором отсутствуют силы взаимодействия между молекулами и пренебрегают объемом самих молекул.
Закон Бойля-Мариотта. При постоянной массе и одной и той же температуре плотность идеального газа изменяется прямо пропорционально, а удельный объем – обратно пропорционально давлению газа:
Закон Гей-Люссака. При постоянных давлении и массе удельный объем идеального газа изменяется прямо пропорционально, а его плотность — обратно пропорционально абсолютной температуре газа:
При объединении законов Бойля-Мариотта и Гей-Люссака получают уравнение Клапейрона для 1 кг газа:
где R – газовая постоянная.
Размерность R , в соответствии с последним уравнением,
показывает, что эта величина является работой 1кг газа при постоянном давлении и изменении его температуры на 1К. Для идеального газа величина R зависит только от природы рабочего вещества.
Таким образом, уравнение Клапейрона связывает три основных термодинамических параметра: p, v, T и обычно используется для определения неизвестного параметра по двум заданным. Поэтому оно называется уравнением состояния идеального газа или его характеристическим уравнением.
Для G кг газа уравнение состояния:
Закон Авогадро. При одинаковых температурах и давлениях в равных объёмах различных идеальных газов содержится одинаковое количество молекул.
Масса газа в килограммах, численно равная молекулярной массе, называется: килограмм-молекула или киломоль (кмоль). Из закона Авогадро следует, что произведение v (т.е. объём одного киломоля, где кг/кмоль – молекулярная масса однородного газа, а для смеси кажущаяся молекулярная или средняя молекулярная масса) есть величина одинаковая для всех газов и газовых смесей при одинаковых p и T . При нормальных физических условиях
Уравнение состояния для 1 кмоль газа называется уравнением Клапейрона-Менделеева и имеет вид
где V = V , при этом
Величина R является универсальной газовой постоянной, одинаковой для киломоля любого однородного газа или газовой смеси. Универсальная газовая постоянная для 1кг газа ( R ) определяется из соотношения[3]
Идеальный газ – математическая модель газа , в которой предполагается , что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией . Между молекулами не действуют силы притяжения или отталкивания , соударения частиц между собой и со стенками сосуда абсолютно упруги , а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями .
Реальный газ отличается от идеального наличием взаимодействия молекул. При малых плотностях в нем преобладают силы притяжения, что приводит к появлению дополнительного давления: газ как бы сжимает сам себя. При больших плотностях действуют силы отталкивания, в следствие чего молекула не допускает проникновения других молекул в занимаемый ею объем. Пренебрегать собственным объемом молекул реального газа нельзя.
При не слишком высоком давлении и не слишком низкой температуре реальный газ с достаточной степенью точности подчиняется законам идеального газа.
Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разрежении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление, объем и температура.
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров – давление, объем или температура – остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами .
Газовые законы – частный случай уравнения состояния идеального газа , один из параметров которого остается постоянным.
При температуре 27 0С давление газа в закрытом сосуде было 75 кПа. Каким будет давление при температуре равной –13°С?
Видео:Физика. 10 класс. Уравнение состояния идеального газаСкачать

Уравнения состояния реального газа
1.1. Уравнения состояния реального газа
Модель идеального газа хорошо описывает свойства газообразного состояния вещества при средних и высоких температурах (от комнатной и выше) и небольших давлениях (около атмосферного). Расчет свойств газов в широком интервале экспериментальных условий требует использования уравнения состояния реального газа[1].
Реальным газом называется газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия. Оно имеет электромагнитную и квантовую природу и осуществляется посредством сил межмолекулярного притяжения и отталкивания.
Силы притяжения, проявляющиеся на расстояниях r между центрами молекул порядка 10 -7 см, называются ван-дер-ваальсовыми силами. Они убывают с расстоянием r –7 , что соответствует изменению потенциальной энергии по закону r –6 .
Различают три вида ван-дер-ваальсовых сил [7]:
Ориентационные силы между двумя молекулами, обладающими постоянными дипольными моментами. Они стремятся расположить молекулы упорядоченно так, чтобы векторы дипольных моментов ориентировались вдоль одной прямой. Этому препятствует тепловое движение молекул.
Индукционные силы, возникающие между молекулами, обладающими высокой поляризуемостью. Если молекулы достаточно сближены, то под действием электрического поля одной из них в другой возникает индуцированный дипольный момент.
Дисперсионные силы возникают в результате возбуждения колебаний электронов в молекуле (атоме) под влиянием колебаний электронов в другой молекуле (атоме). Колебания электронов соседних молекул происходят в одинаковой фазе и приводят к притяжению двух молекул (атомов). Величина дисперсионных сил определяется нулевой энергией молекул (атомов), если их колебания можно рассматривать как колебания линейных гармонических осцилляторов.
Полная потенциальная энергия ван-дер-ваальсовых сил описывается суммой:
Для полярных молекул основную роль играют ориентационные силы притяжения, для остальных молекул – дисперсионные силы. Энергия ван-дер-ваальсового притяжения составляет (0,1 – 1) ккал/моль [7]. В большинстве случаев ван-дер-ваальсовы силы притяжения перекрываются значительно превосходящими их химическими валентными силами притяжения с энергиями порядка (10 – 100) ккал/моль.
Согласно упрощенной модели ван-дер-ваальсовых сил, молекулы газа – абсолютно упругие шары – притягиваются с силами, достигающими наибольшего значения при непосредственном их соприкосновении. Силы отталкивания проявляют себя на значительно меньших расстояниях.
Для описания свойств реальных газов применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева. Наиболее удобны двухпараметрические уравнения, разрешимые относительно давления и содержащие объем в третьей степени (кубические уравнения состояния). Первое такое уравнение было предложено Ван-дер-Ваальсом в 1873 г.
Уравнение Ван-дер-Ваальса состояния реального газа имеет следующий вид [7]:
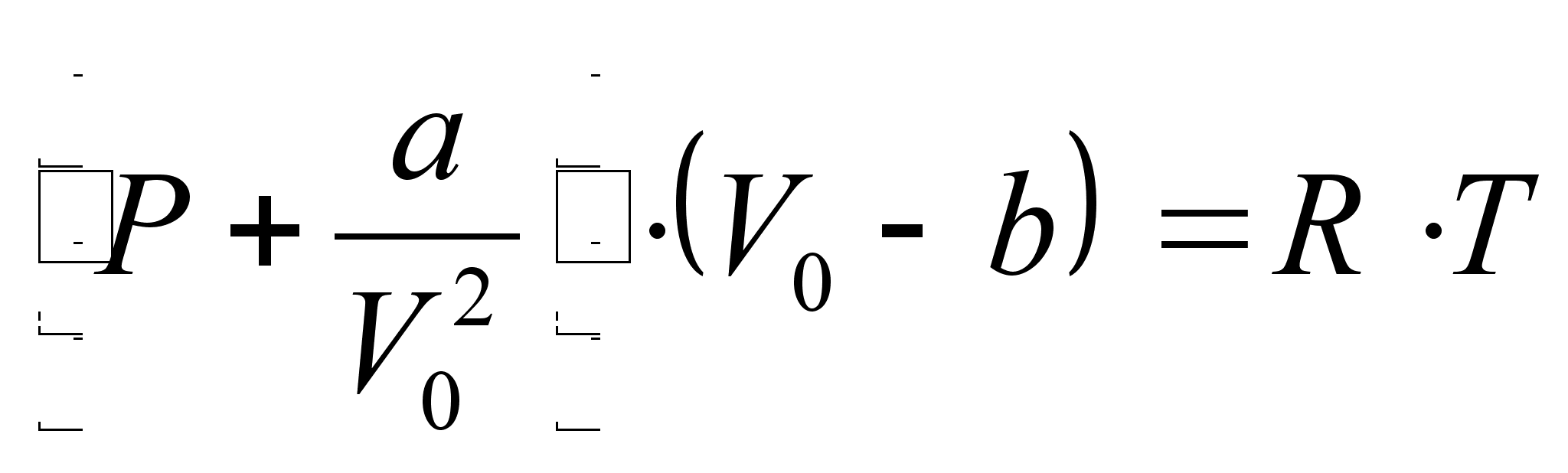
где V0 – объем 1 моля газа, а 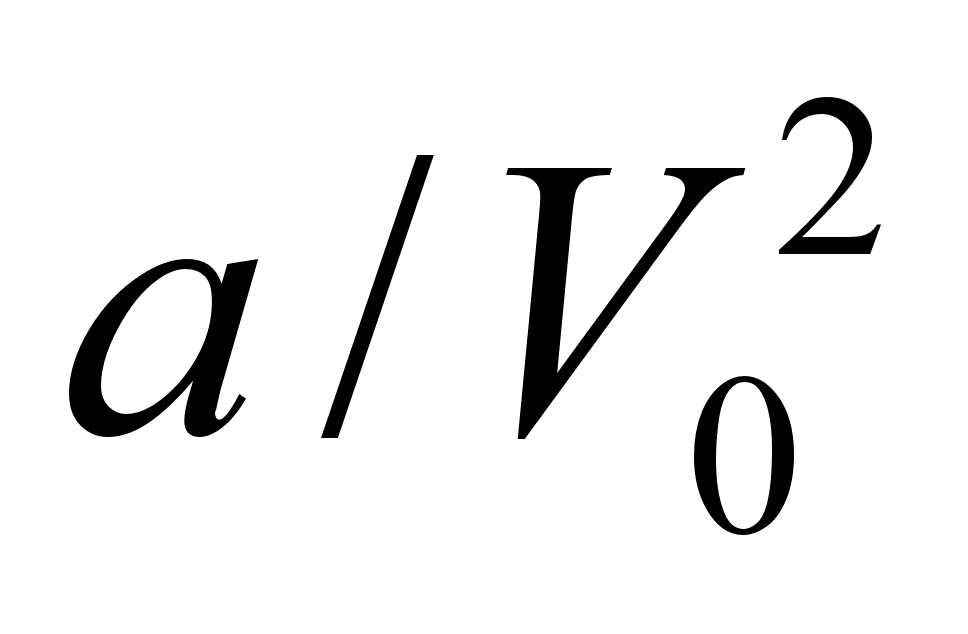
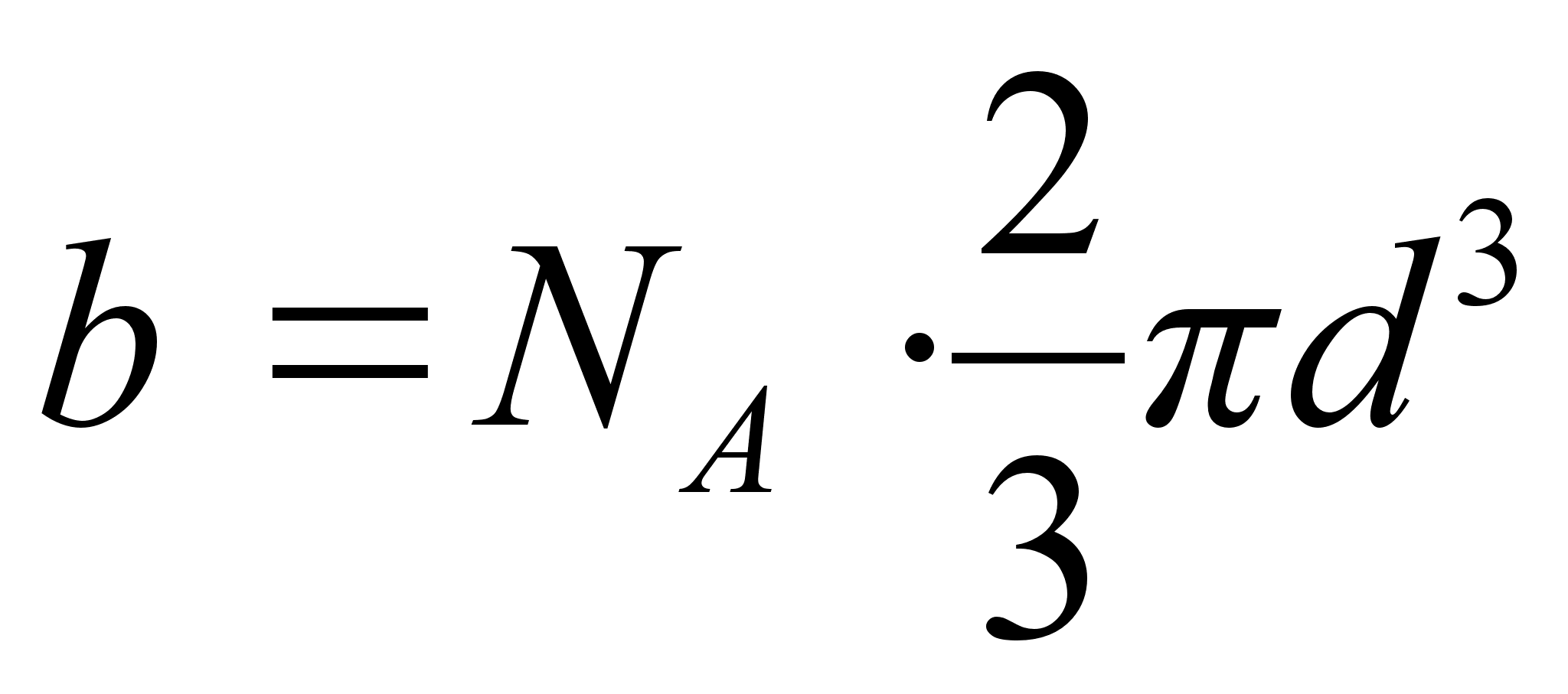
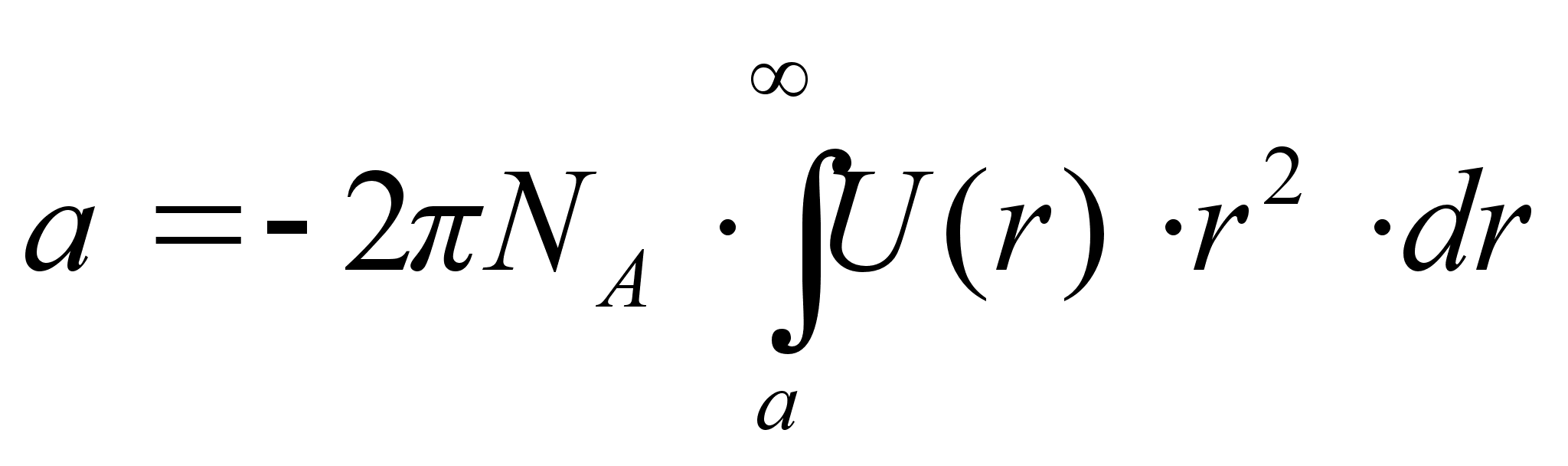
Здесь NA – число Авогадро, d – диаметр молекулы, U(r) – потенциальная энергия притяжения двух молекул.
Уравнение состояния Бертло (1900г.):

Здесь а и b связаны с параметрами критического состояния (в критической точке) соотношениями [8]:
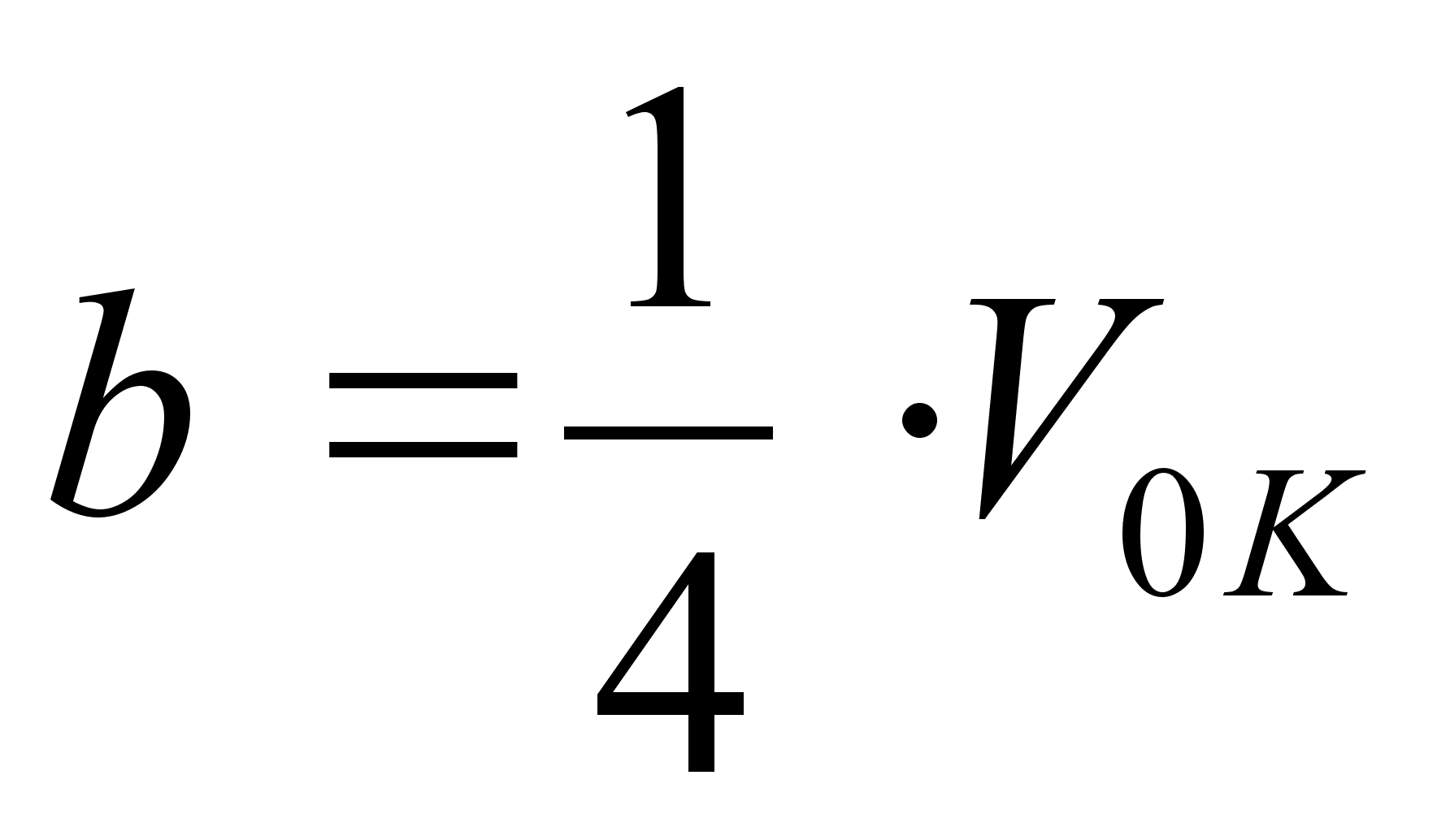
Уравнение состояния Вукаловича и Новикова [7]:
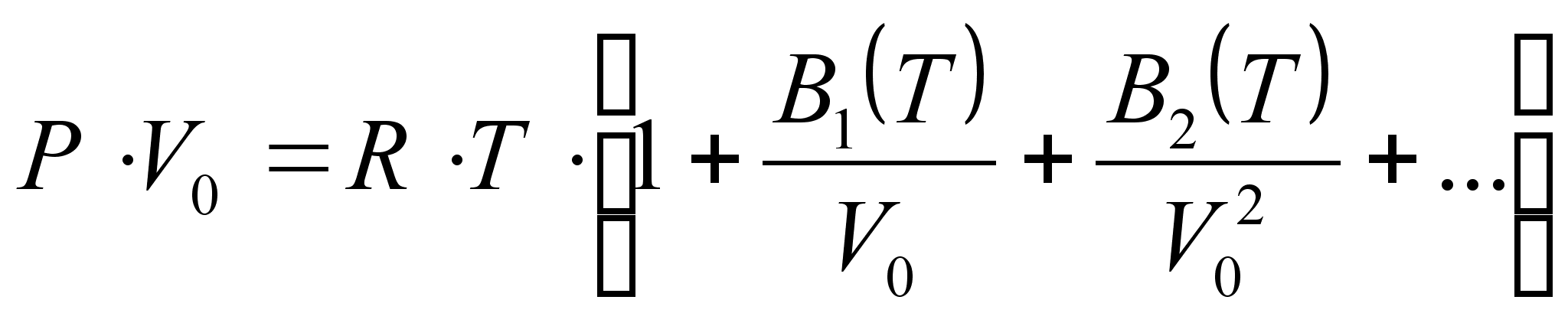
Здесь B1, B2 и т.д. – так называемые вириальные коэффициенты весьма сложного вида. Их вычисление производится с учетом ассоциации молекул – объединения под влиянием ван-дер-ваальсовых сил притяжения.
Уравнение состояния Майера [7]:

где: 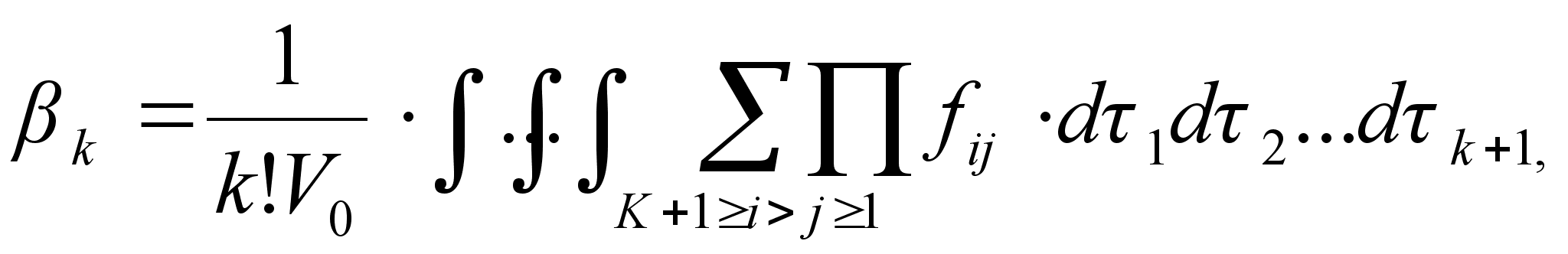
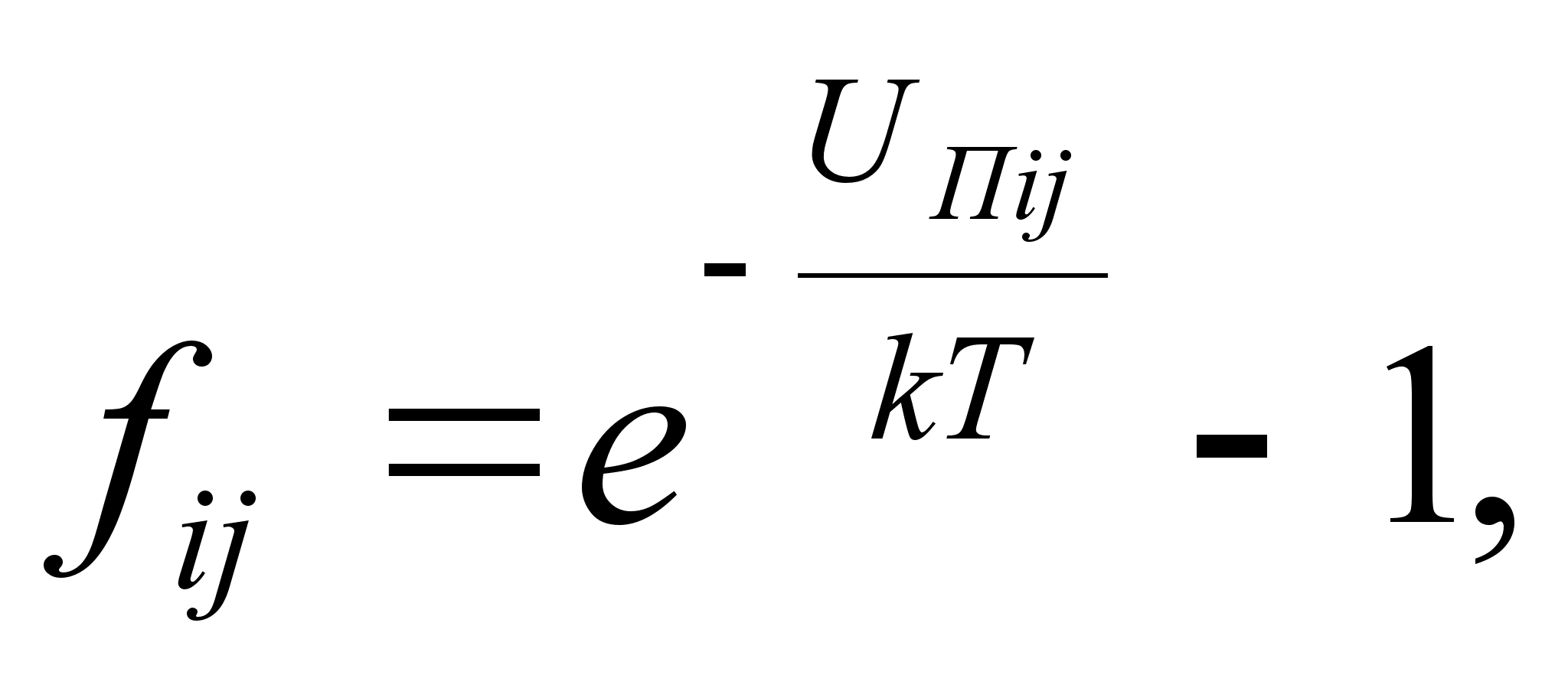
Здесь Uпij – взаимная потенциальная энергия i-й и j-й молекул, взаимодействующих по закону центральных сил, qi1. qin – обобщенные координаты i-той молекулы, обладающей n степенями свободы.
Уравнение Камерлинг-Оннеса (1901) [8]:
где 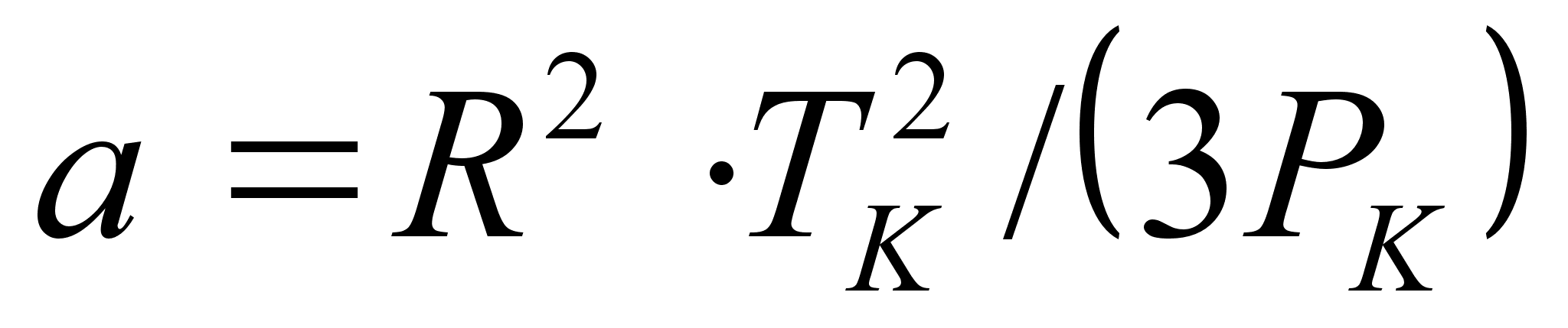
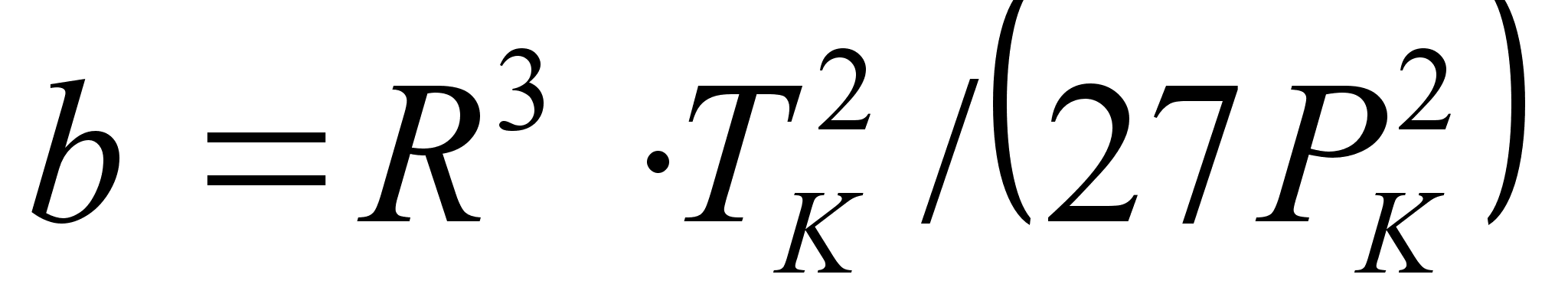
Уравнение Редлиха-Квонга (1949 г.) [8]:
Здесь 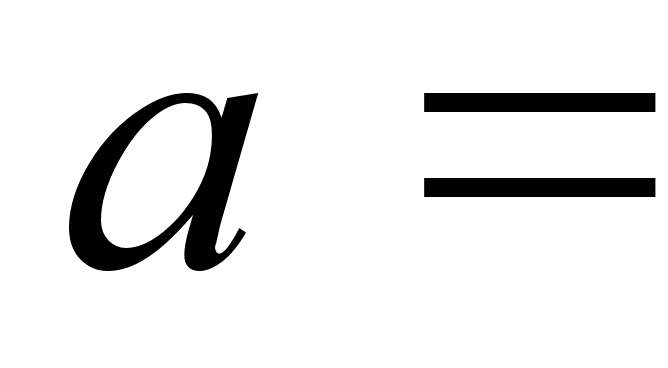
Уравнение Мартина (1967 г.) [8]:
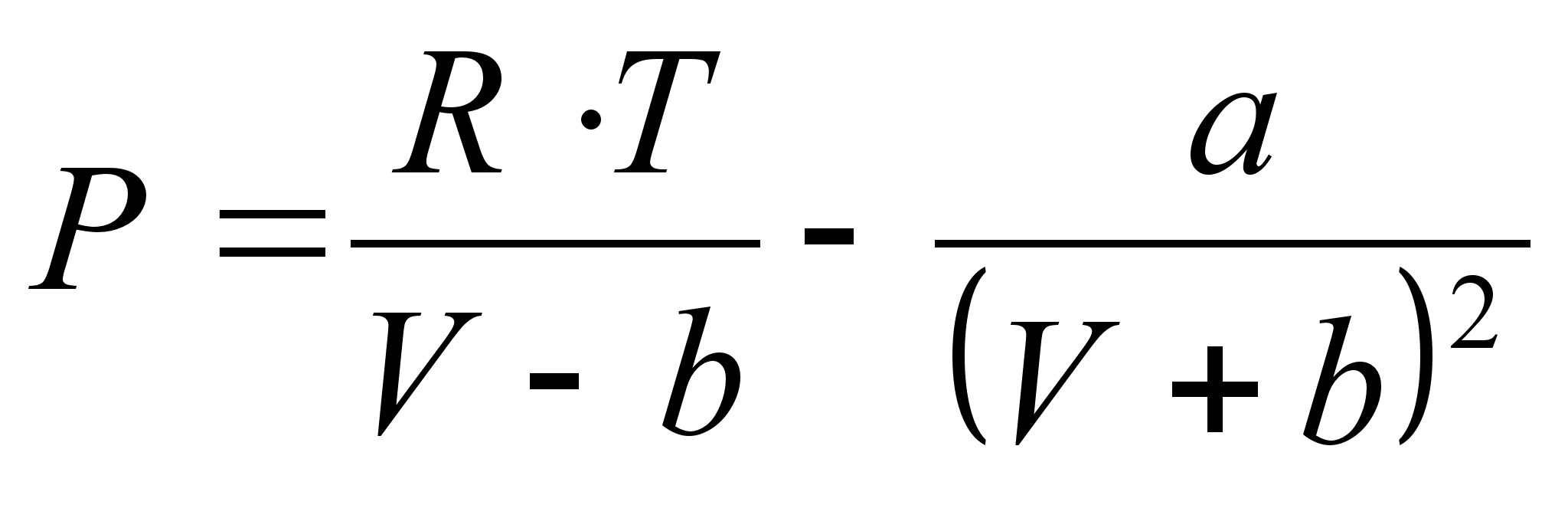
где 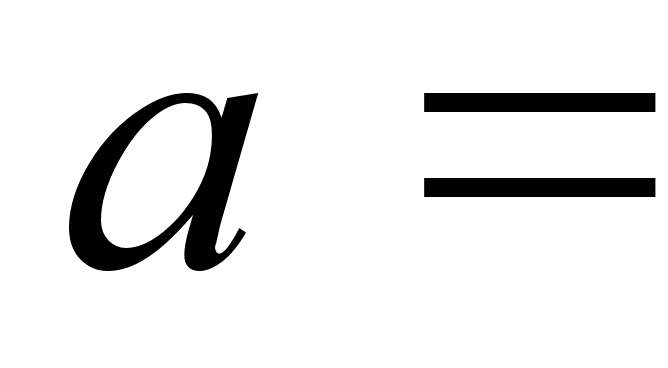
🌟 Видео
10 класс, 4 урок, Уравнение состояния идеального газаСкачать

Уравнение состояния идеального газаСкачать

ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать

Физика - Газовые законы. Уравнение идеального газа.Скачать

ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

10 класс урок №39 Уравнение состояния идеального газаСкачать

2.1.4 Уравнение состояния идельного газаСкачать

Уравнение состояния идеального газаСкачать

Физика Уравнение состояния идеального газаСкачать
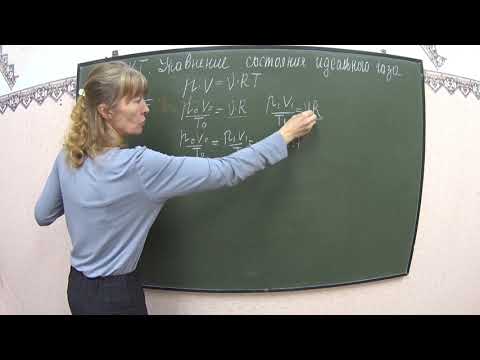


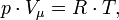
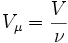 , где где ν — количество вещества, а
, где где ν — количество вещества, а 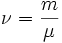 , где m — масса, μ — молярная масса, уравнение состояния можно записать:
, где m — масса, μ — молярная масса, уравнение состояния можно записать: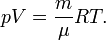
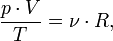
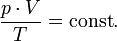
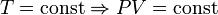 — закон Бойля — Мариотта.
— закон Бойля — Мариотта.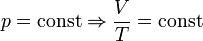 — закон Гей-Люссака.
— закон Гей-Люссака.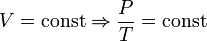 — закон Шарля
— закон Шарля