Уравнение соответствующее правилу де моргана

Видео:Законы де Моргана | 13/50 урок Информатики | ШколковоСкачать

A10 (базовый уровень, время – 1 мин)

Тема: Преобразование логических выражений. Формулы де Моргана.

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ú,Ù, ), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ú,Ù, ), что еще раз подчеркивает проблему.

Что нужно знать:

· условные обозначения логических операций

A, не A (отрицание, инверсия)

A Ù B, A и B (логическое умножение, конъюнкция)

A Ú B, A или B (логическое сложение, дизъюнкция)

A → B импликация (следование)

· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A → B = A Ú B или в других обозначениях A → B =

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»

· правила преобразования логических выражений (слайд из презентации «Логика»):

· фактически это задание на применение законов де Моргана (хотя об этом нигде не говорится):

(A Ù B) = A Ú B

(A Ú B) = A Ù B

Пример задания:

Укажите, какое логическое выражение равносильно выражению A Ù (B Ú C).

Решение (вариант 1, использование законов де Моргана):

1) перепишем заданное выражение и ответы в других обозначениях:
заданное выражение
ответы: 1) 2) 3) 4)

2) посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

а затем используем закон двойного отрицания по которому :

3) таким образом, правильный ответ – 3 .

Возможные ловушки и проблемы:

· серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид; при этом сразу становится понятно, что ответы 1 и 2 заведомо неверные

· при использовании законов де Моргана часто забывают, что нужно заменить «И» на «ИЛИ» и «ИЛИ» на «И» (возможный неверный ответ )

· расчет на то, что при использовании законов де Моргана инверсия сложного выражения по ошибке «просто пропадет», и все сведется к замене «ИЛИ» на «И» (неверный ответ )

· иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений

Решение (вариант 2, через таблицы истинности, если забыли формулы де Моргана):

1) перепишем заданное выражение в других обозначениях:
заданное выражение
ответы: 1) 2) 3) 4)

2) для доказательства равносильности двух логических выражений достаточно показать, что они принимают равные значения при всех возможных комбинациях исходных данных; поэтому можно составить таблицы истинности для исходного выражения и всех ответов и сравнить их

3) здесь 3 переменных, каждая из которых принимает два возможных значения (всего 8 вариантов, которые в таблице истинности записывают по возрастанию двоичных кодов – см. презентацию «Логика»)

4) исходное выражение истинно только тогда, когда и , то есть только при . (в таблице истинности одна единица, остальные – нули)

5) выражение истинно, если хотя бы одна из переменных равна нулю, то есть, оно будет ложно только при (в таблице истинности один нуль, остальные – единицы)

6) аналогично выражение ложно только при , а в остальных случаях – истинно

7) выражение истинно только при , а в остальных случаях – ложно

8) выражение истинно только при , а в остальных случаях – ложно

9) объединяя все эти результаты в таблицу, получаем:

Видео:Какие есть правила де Моргана? Душкин объяснитСкачать

Тема : Преобразование логических выражений. Формулы де Моргана

Главная > Документ

© К. Поляков, 2009-2010

Видео:Законы де Моргана || Формулы де Моргана || Правило де МорганаСкачать

A10 (базовый уровень, время – 1 мин)

Тема : Преобразование логических выражений. Формулы де Моргана.

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (  ,  , ¬ ), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает  и  . Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (  ,  , ¬ ), что еще раз подчеркивает проблему.

Что нужно знать :

условные обозначения логических операций

¬ A , не A (отрицание, инверсия)

A  B , A и B (логическое умножение, конъюнкция)

A  B , A или B (логическое сложение, дизъюнкция)

A → B импликация (следование)

операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A → B = ¬ A  B или в других обозначениях A → B =

если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»

правила преобразования логических выражений (слайд из презентации «Логика»):

фактически это задание на применение законов де Моргана (хотя об этом нигде не говорится):

¬ ( A  B ) = ¬ A  ¬ B

¬ ( A  B ) = ¬ A  ¬ B

Пример задания:

Укажите, какое логическое выражение равносильно выражению A  ¬(¬B  C) .

1) ¬A  ¬B  ¬C 2) A  ¬B  ¬C 3) A  B  ¬C 4) A  ¬B  C

Решение (вариант 1, использование законов де Моргана):

перепишем заданное выражение и ответы в других обозначениях:
заданное выражение
ответы: 1) 2) 3) 4)

посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

а затем используем закон двойного отрицания по которому :

таким образом, правильный ответ – 3 .

Возможные ловушки и проблемы :

серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид; при этом сразу становится понятно, что ответы 1 и 2 заведомо неверные

при использовании законов де Моргана часто забывают, что нужно заменить «И» на «ИЛИ» и «ИЛИ» на «И» (возможный неверный ответ )

расчет на то, что при использовании законов де Моргана инверсия сложного выражения по ошибке «просто пропадет», и все сведется к замене «ИЛИ» на «И» (неверный ответ )

иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений

Решение (вариант 2, через таблицы истинности, если забыли формулы де Моргана):

перепишем заданное выражение в других обозначениях:
заданное выражение
ответы: 1) 2) 3) 4)

для доказательства равносильности двух логических выражений достаточно показать, что они принимают равные значения при всех возможных комбинациях исходных данных; поэтому можно составить таблицы истинности для исходного выражения и всех ответов и сравнить их

здесь 3 переменных, каждая из которых принимает два возможных значения (всего 8 вариантов, которые в таблице истинности записывают по возрастанию двоичных кодов – см. презентацию «Логика»)

исходное выражение истинно только тогда, когда и , то есть только при . (в таблице истинности одна единица, остальные – нули)

выражение истинно, если хотя бы одна из переменных равна нулю, то есть, оно будет ложно только при (в таблице истинности один нуль, остальные – единицы)

аналогично выражение ложно только при , а в остальных случаях – истинно

выражение истинно только при , а в остальных случаях – ложно

выражение истинно только при , а в остальных случаях – ложно

объединяя все эти результаты в таблицу, получаем:

Видео:3.8 Де Морган правилаСкачать

Как доказать законы Де Моргана

Как доказать законы Де Моргана — Науки

Видео:2.4 Разность множеств, законы де Моргана | Константин Правдин | ИТМОСкачать

Содержание:

В математической статистике и вероятности важно знать теорию множеств. Элементарные операции теории множеств связаны с определенными правилами вычисления вероятностей. Взаимодействие этих элементарных множественных операций объединения, пересечения и дополнения объясняется двумя утверждениями, известными как законы Де Моргана. Изложив эти законы, мы увидим, как их доказать.

Видео:Законы де Моргана. ЛогикаСкачать

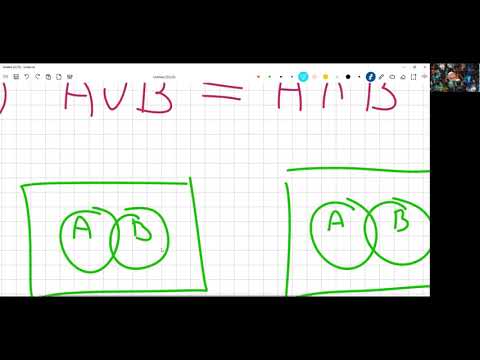
Заявление о законах Де Моргана

Законы Де Моргана относятся к взаимодействию союза, пересечения и дополнения. Напомним, что:

• Пересечение множеств А а также B состоит из всех элементов, общих для обоих А а также B. Пересечение обозначается через А ∩ B.
• Объединение множеств А а также B состоит из всех элементов, которые либо А или B, включая элементы в обоих наборах. Пересечение обозначается A U B.
• Дополнение набора А состоит из всех элементов, которые не являются элементами А. Это дополнение обозначается A C .

Теперь, когда мы вспомнили об этих элементарных операциях, мы увидим формулировку законов Де Моргана. Для каждой пары наборов А а также B

1. (А ∩ B) C = А C U B C .
2. (А U B) C = А C ∩ B C .

Видео:Правила Де Моргана. Доказательство. Теория множеств.Скачать

Схема стратегии доказательства

Прежде чем перейти к доказательству, мы подумаем, как доказать приведенные выше утверждения. Мы пытаемся продемонстрировать, что два набора равны друг другу. В математическом доказательстве это делается с помощью процедуры двойного включения. Схема этого метода доказательства такова:

1. Покажите, что набор слева от нашего знака равенства является подмножеством набора справа.
2. Повторите процесс в обратном направлении, показывая, что набор справа является подмножеством набора слева.
3. Эти два шага позволяют нам сказать, что наборы фактически равны друг другу. Они состоят из одних и тех же элементов.

Видео:Законы алгебры логики / Закон де Моргана + доказательство [Алгебра логики] #5Скачать

Доказательство одного из законов

Мы увидим, как доказать первый из приведенных выше законов Де Моргана. Начнем с того, что покажем, что (А ∩ B) C это подмножество А C U B C .

1. Сначала предположим, что Икс является элементом (А ∩ B) C .
2. Это значит, что Икс не является элементом (А ∩ B).
3. Поскольку пересечение — это совокупность всех элементов, общих для обоих А а также B, предыдущий шаг означает, что Икс не может быть элементом обоих А а также B.
4. Это значит, что Икс должен быть элементом хотя бы одного из множеств А C или B C .
5. По определению это означает, что Икс является элементом А C U B C
6. Мы показали включение желаемого подмножества.

Наше доказательство наполовину сделано. Чтобы завершить его, мы показываем включение противоположного подмножества. В частности, мы должны показать А C U B C является подмножеством (А ∩ B) C .

1. Начнем с элемента Икс в наборе А C U B C .
2. Это значит, что Икс является элементом А C или это Икс является элементом B C .
3. Таким образом Икс не является элементом хотя бы одного из множеств А или B.
4. Так Икс не может быть элементом обоих А а также B. Это значит, что Икс является элементом (А ∩ B) C .
5. Мы показали включение желаемого подмножества.

Видео:Законы де Моргана | Алгебра логики | Информатика с МанеСкачать

Доказательство иного закона

Доказательство другого утверждения очень похоже на доказательство, которое мы изложили выше.Все, что нужно сделать, это показать подмножество, включающее множества по обе стороны от знака равенства.

💡 Видео

ЗАКОНЫ АЛГЕБРЫ ЛОГИКИСкачать

Законы Де Моргана / Как упростить / Подготовка к Мэску Информатика / НИШ 12 КлассСкачать

Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать

DE MORGAN'S THEOREMСкачать

Множества и операции над нимиСкачать

De Morgan's law in Boolean AlgebraСкачать

Равносильность формул. Легко и просто.Скачать

Лекция 67. Теорема де МорганаСкачать

Лекция 1. Определение множества. Законы де Моргана. Парадокс Рассела. Теорема ВейерштрассаСкачать

Закон поглощения + доказательство. Преобразование логических выражений [Алгебра логики] #7Скачать

DeMorgan's TheoremСкачать