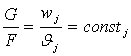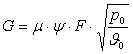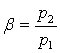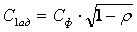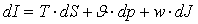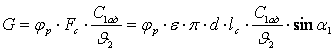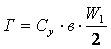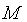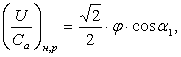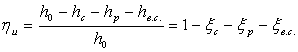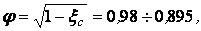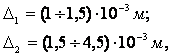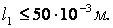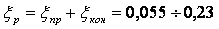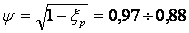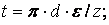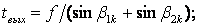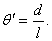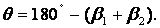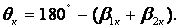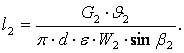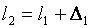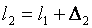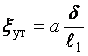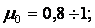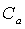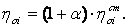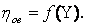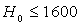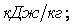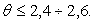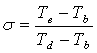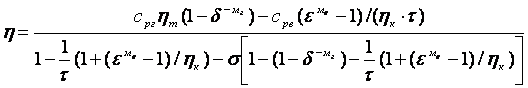Преобразование энергии в турбинной ступени, а также энергетические характеристики других элементов проточной части турбины описываются в общем случае на основе законов течения сжимаемой жидкости, которые изучаются в курсе гидрогазодинамики. В основном используются законы одномерного движения, под которым понимают такое движение жидкости, когда во всех точках поперечного сечения канала параметры жидкости (скорость, давление, удельный объем и др.) можно считать постоянным, а изменение параметров происходит вдоль канала. В реальных потоках рабочего тела в паровых турбинах параметры в поперечном сечении канала не сохраняются постоянными. Например, скорость потока вблизи стенок вследствие трения всегда ниже, чем в ядре потока.
Вторым существенным допущением при расчете потоков в проточной части турбины является предположение о неизменности параметров потока во времени, т.е. поток рассматривается установившимся.
Кроме этого делаются и другие допущения – например, об отсутствии теплообмена между потоком и стенками каналов и др.
Основными уравнениями одномерного движения сжимаемой жидкости являются:
1) уравнение состояния: 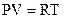
2) уравнение неразрывности, расхода, сплошности: 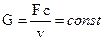
где F – площадь поперечного сечения; c – скорость; v – удельный объем.
3) уравнение количества движения: 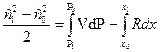
4) уравнение сохранения энергии: 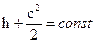
Одномерные течения в каналах разделяются на конфузорные и диффузорные.
Конфузорными называются такие течения в каналах, когда скорость рабочего тела на выходе становится больше, чем скорость на входе.
Диффузорными называются течения, в которых скорость рабочего тела уменьшается в направлении потока.
Основные уравнения одномерных потоков позволяют рассчитывать течения в каналах турбомашин. Из уравнения сохранения энергии следует, что при конфузорном течении, например, в соплах турбины, вдоль потока вместе с увеличением скорости рабочего тела уменьшается его энтальпия; в диффузорных потоках, наоборот, энтальпия растет, т.к. скорость падает.
Для расчетов одномерных потоков в каналах вводят параметры полного торможения потока в данном его сечении. Под ними в каком либо сечении понимают фиктивные параметры, которые достигаются при полном изоэнтропном торможении потока от состояния в этом сечении до нулевой скорости.
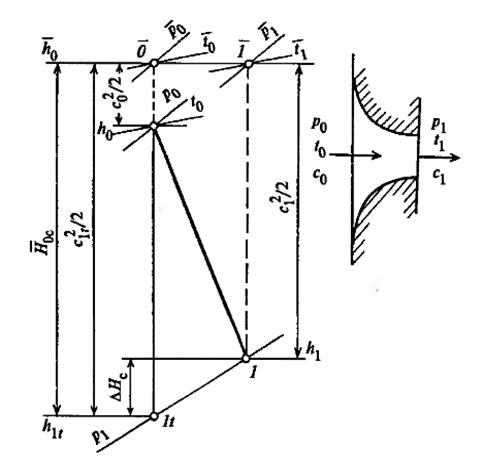
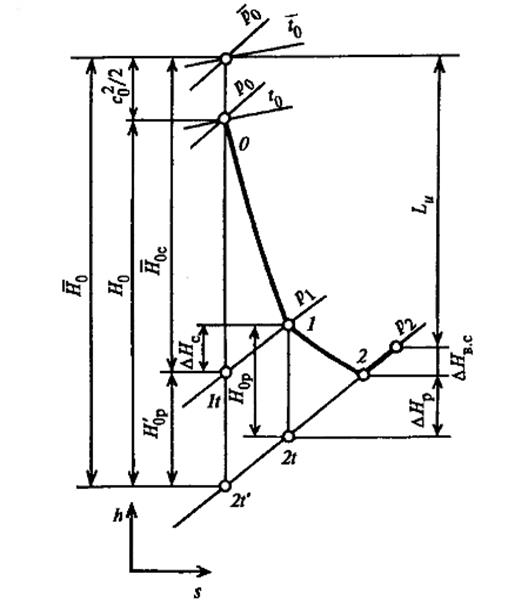
Параметры полного торможения могут быть подсчитаны с помощью h,s-диаграммы. Изобразим процесс течения рабочего тела в сопловом канале в h,s-диаграмме (рис.21).
Параметры во входном сечении сопла обозначены с индексом О, а в сечении на выходе из сопла с индексом 1, если течение реальное с потерями энергии, и с индексом 1t, если течение предполагается изоэнтропным (без потерь энергии).
Для определения скорости на выходе из соплового канала при изоэнтропном течении используем уравнение энергии, записанное для входного и выходного сечений сопла: 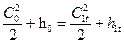
откуда теоретическая скорость на выходе из сопла 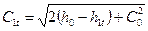
где 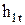
Рисунок 21 – Процесс изменения состояния в h,s–диаграмме при
истечении пара или газа через сопло
Действительная скорость потока (с потерями энергии) на выходе из сопла определяется по аналогичной формуле, полученной из уравнения энергии, записанного для входного и выходного сечений сопла по действительным параметрам потока за соплом 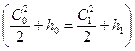
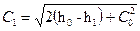
Разность энтальпий 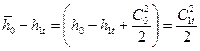
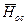
Для определения параметров полного торможения во входном сечении сопла следует на h,s-диаграмме от точки О вверх по изоэнтропе отложить отрезок 
Через точку 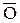

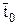
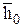
Аналогично для определения параметров полного торможения в выходном сечении сопла следует отложить в h,s-диаграмме от точки 1 вверх по изоэнтропе отрезок 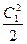
Таким образом, в потоках с потерями кинетической энергии давление полного торможения уменьшается вдоль потока.
В отличие от параметров полного торможения 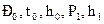
Разность энтальпий 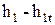
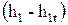
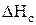
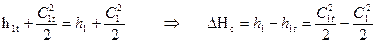
Каналы, в которых происходит плавное преобразование энтальпии в кинетическую энергию, т.е. в которых происходит ускорение потока, называется сопловыми или просто соплами.
Для характеристики потоков важными являются понятия скорости звука и критической скорости потока: 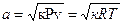
Критической скоростью потока 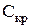
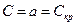
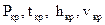
Как следует из 

Для расчетов потока важными являются безразмерные параметры потока. К ним относятся: относительное давление 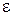
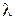
М=С/а — отношение скорости потока к скорости звука в данном сечении называется числом Маха.

Между любыми двумя безмерными параметрами легко устанавливаются функциональные зависимости, которые носят название газодинамических функций, приведенных в справочной литературе и известных из курса гидрогазодинамики.
Поскольку в состав турбинной ступени входят турбинная решетка, то вкратце остановимся на ее рассмотрении.
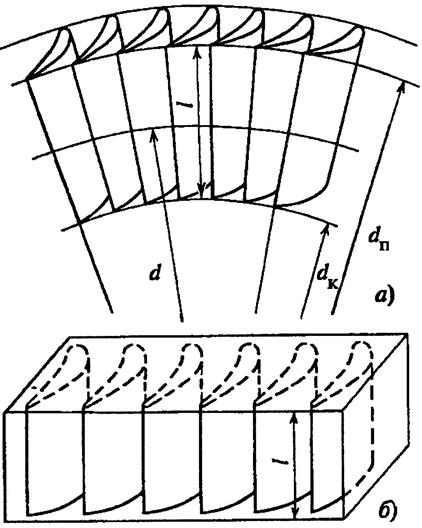
В паровых турбинах широко используется кольцевые турбинные решетки (рис.22), представляющие собой систему каналов, образованную установленными по кольцу одинаковыми профилями специальной формы. Все профили в решетке одинаковы, их устанавливают на равном расстоянии друг от друга и одинаковым образом. В результате между профилями образуются каналы, через которые вытекает пар.
Рисунок 22 — Модели турбинных решеток: а – кольцевой; б – прямой (плоской)
Путем изменения формы профилей и расположения их в решетке можно получать необходимую форму каналов (рис.23).
Рисунок 23 — Развертки профилей турбинных решеток: а, б — с каналами сильно и слабо уменьшающегося сечения; в — с каналами типа сопла Лаваля
Входная часть профиля называется входной кромкой, выходная – выходной кромкой, выпуклая часть – спинкой или стороной разрежения, вогнутая — стороной давления. Выходная часть канала называется косым срезом.
Течение пара в турбинных решетках подчиняется общим закономерностям, рассмотренным ранее.
Потери энергии, возникающие при течении пара через турбинную решетку, условно можно разделить на несколько составляющих. Значительную долю потерь составляют профильные, которые возникают при обтекании потоком профилей за счет появления сил трения. Имеют место также концевые потери, возникающие в концевых областях лопаток и вызывающие появление вихрей. За счет улучшения профиля лопаток, их лучшего обтекания потоком, понижаются потери.
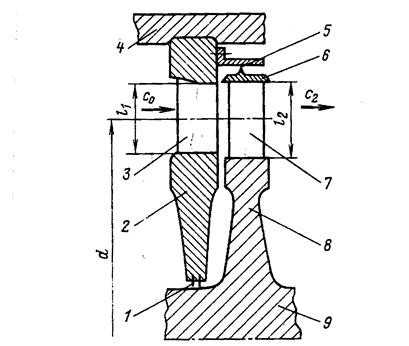
Под турбинной ступенью, как отмечалось ранее, понимается совокупность неподвижного ряда сопловых лопаток, в каналах которых ускоряется поток пара или газа, и подвижного ряда рабочих лопаток, в которых энергия движущегося пара или газа преобразуется в механическую работу на вращающемся роторе по преодолению сил сопротивления приводимой машины. На рис.24 приведено схематическое изображение турбинной ступени.
Турбинная ступень характеризуется средним диаметром ступени d и высотами сопловых l1 и рабочих l2 лопаток.
Сопловые лопатки со строго одинаковым шагом установлены в диафрагме, представляющей собой плоское, разрезанное по горизонтальному диаметру, кольцо. Сопловые лопатки образуют кольцевую решетку.
Рабочие лопатки с помощью хвостовиков набираются на диске, откованном заодно с валом или посаженном на него с натягом. Подобно сопловым лопаткам, рабочие лопатки образуют кольцевую решетку. Соседние лопатки решетки образуют рабочие каналы, через которые проходят струи пара, выходящие из сопловой решетки.
Рисунок 24 — Схематическое изображение турбинной ступени:
1 – диафрагменное уплотнение; 2 – диафрагма; 3 – сопловая решетка; 4 – корпус турбины; 5 – надбандажное уплотнение; 6 – ленточный бандаж; 7 – рабочая решетка; 8 – диск; 9 – вал
Рабочие лопатки, набранные на диске, обычно связаны по вершинам с помощью ленточного бандажа в пакеты по 2-14 шт. для увеличения надежности и экономичности ступени. Поверх бандажа часто устанавливают уплотнения для уменьшения утечки пара над бандажом. Аналогичное уплотнение устанавливают между диафрагмой и валом.
При истечении пара из сопла в среду с пониженным давлением его потенциальная энергия переходит в кинетическую. Именно такой процесс происходит в сопловых каналах турбинной установки. За счет понижения давления от значения 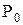
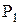
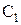
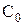
На выходе из сопловых лопаток рабочее тело (пар или газ) приобретает в процессе расширения скорость 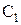
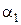
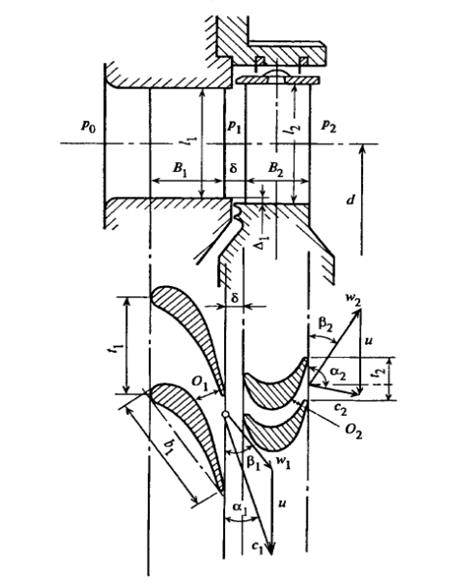
Рисунок 25 — Проточная часть осевой ступени и развертка цилиндрического сечения по среднему диаметру ступени : 
Значение этой скорости зависит от диаметра d, на котором расположены рабочие лопатки, и от частоты вращения ротора n: 
На входе в рабочие лопатки рабочее тело в относительном движении перемещается с относительной скоростью 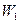
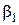
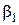
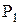
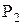
На выходе из каналов рабочих лопаток относительная скорость рабочего тела обозначается 
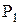
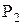


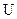
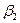
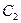
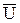
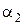

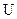
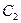
Рассмотрим процесс течения рабочего тела в турбинной ступени в h,s-диаграмме (рис.26).
Расширение рабочего тела в сопловых каналах ступени от состояния перед ступенью, определяемое точкой О, до точки 1t соответствует теоретическому (изоэнтропному) процессу течения в соплах. Реальный процесс в соплах сопровождается потерями энергии 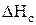
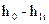
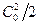
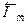
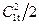
В соответствии с уравнением энергии теоретическая скорость потока на выходе из сопл определяется по формуле: 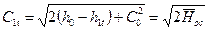
Действительная скорость истечения из сопл из-за потерь энергии в соплах меньше теоретической 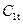
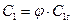
где 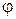
Теоретический процесс расширения рабочего тела в рабочих лопатках изображается линией от точки 1 до точки 2t; разность ( 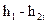
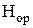
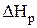
Рисунок 26 – Процесс течения пара (газа) в турбинной ступени в h,s–диаграмме
Для потока в относительном движении в каналах рабочих лопаток уравнение сохранения энергии для сечений на входе и выходе из каналов рабочих лопаток запишется в следующем виде: 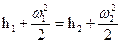
В правой части этого уравнения отсутствует член, характеризующий отводимую от рабочих лопаток к ротору турбины механическую работу, т.к. механическая работа силы взаимодействия между лопаткой и потоком в координатах движущейся лопатки равна нулю. Действительно, точка приложения этой силы не перемещается по отношению к наблюдателю, вращающемуся вместе с рабочими лопатками (условно). Перемещение точки приложения силы входит сомножителем в выражение механической работы.
По аналогии с предыдущими формулами получим выражение для определения теоретической скорости потока в относительном движении на выходе из рабочих лопаток: 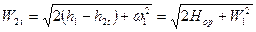
Действительная скорость на выходе из рабочих лопаток будет меньше теоретической 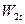
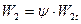
где 
Потери энергии 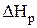
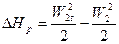
Отрезок 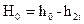

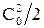

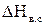
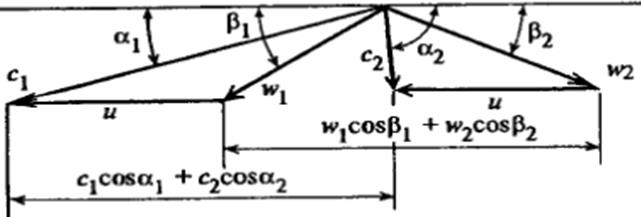
Треугольники скоростей на входе и выходе из рабочих лопаток при расчете турбинной ступени обычно совмещают вершинами в одну точку.
Для построения треугольников скоростей (рис.27) угол 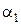
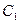
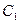
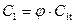
Окружную скорость по формуле:
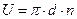
где d – средний диаметр ротора, м;
n- частота вращения ротора, 1/с.
Рисунок 27 — Треугольники скоростей для потока пара (газа) в одновенечной турбинной ступени
Из геометрии входного треугольника скоростей определяют относительную скорость 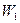
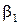
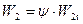
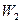
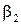
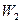
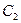
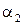
Соотношения между скоростями и углами потока в турбинной ступени в большой степени зависят от степени реактивности ступени 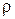

Чем выше степень реактивности 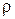
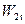
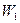

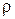
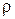
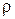
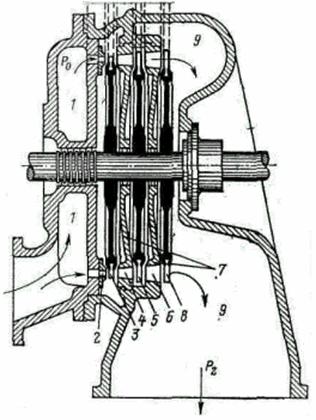
Как правило, чисто активные ступени ( 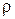
В специальных случаях применяются ступени с отрицательной степенью реактивности. В рабочих лопатках ступени с
Дата добавления: 2014-12-30 ; просмотров: 6968 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Алматы 2008
Цель курса –освоение студентами принципа работы, устройства паровых и газовых турбин, относящихся к основному оборудованию тепловых и атомных электростанций, газотурбинных электрических и газоперекачивающих станций.
Задача курса – усвоение студентами основ теории и конструкций паровых и газовых турбин, применяемых в технологических цепочках тепловых и атомных электрических станций, промышленных предприятий.
В результате изучения дисциплины студенты должны:
— об условиях работы основных элементов паровых и газовых турбин;
— о принципах конструирования лопаточных машин;
— о технологии изготовления деталей паровых и газовых турбин;
— суть теории лопаточных машин (вентиляторов, нагнетателей, компрессоров, турбин);
— конструктивное устройство паровых и газовых турбин;
— тепловые и прочностные процессы в проточных частях и деталях лопаточных машин и основы их расчета;
— рассчитывать и выбирать паровые и газовые турбины в зависимости от их назначения;
— проводить тепловые и прочностные расчеты нагнетателей и тепловых двигателей.
Энергетика — одна из ведущих отраслей народного хозяйства страны. Ведущая роль в деле энергообеспечения республики принадлежит тепловым электрическим станциям. Для привода электрогенераторов используются турбины, как правило, паровые. Современные тепловые турбинные установки существуют в двух основных разновидностях: паровые и газовые. Курс «Паровые и газовые турбины» является базовым при подготовке бакалавров теплоэнергетиков и от его усвоения во многом определяется понимание профильных курсов.
При изучении курса требуется обратить внимание на то, что в теории турбомашин преобладает эмпирический подход, т.к. поток рабочего тела в лопаточных машинах – всегда пространственный, параметры зависят от времени и координат, а аналитического решения для такой задачи, пока не получено. Поэтому в курсе часто используются опытные графики, диаграммы, номограммы.
При конструировании турбин стремятся получить наибольшую мощность при высоких и сверхкритических параметрах рабочего тела. Мощные турбины должны быть ремонтопригодными, управляемыми в эксплуатации, монтаже и при пусконаладочных работах. Они должны быть надежными, экономичными, маневренными.
Цель, объем и содержание дисциплины. Предмет дисциплины. Основные задачи. Классификация паровых и газовых турбин. История развития паровых и газовых турбин. Области их применения. Устройство типовой многоступенчатой осевой активной паровой турбины [1, 2, 7, 8].
Цель лекции — знакомство с кругом изучаемых вопросов, литературой, рекомендуемой для изучения курса, историей развития турбомашин, классификацией, областью применения и устройством турбомашин.
1.1 Предмет и содержание курса
Для специализации «Тепловые электрические станции» предметом курса является стационарная и станционная теплоэнергетика.
Содержание курса включает основы термодинамики потока, газодинамики, теплопередачи и прочности применительно к паровым и газовым турбинам с учетом различных конструктивных исполнений их деталей, узлов и соединений.
1.2 Классификация паровых турбин
Основным тепловым двигателем ТЭС является турбина – лопаточная расширительная машина непрерывного (ротативного) типа, в которой происходит превращение теплоты и упругостной (потенциальной) энергии нагретого, сжатого рабочего тела (газа или пара), расширяющегося в межлопаточных каналах, в кинетическую энергию, а затем в механическую работу вращения ротора. Выходными параметрами турбины являются механическая мощность и определенное число оборотов (3000 или 1500 об/мин).
По принципу действия турбины делятся на активные и реактивные.
Проточная часть, состоящая из одного ряда сопел и одного ряда рабочих лопаток, образует простейшую турбинную ступень.
В активном варианте ступени расширение рабочего вещества (падение давления) имеет место только в соплах; на рабочих лопатках давление остается постоянным.
Работа осуществляется за счет непосредственного ударного действия потока на лопатки.
Видео:ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать

Реактивные турбины
Расширение рабочего вещества имеет постепенный характер: давление частично падает в соплах, а затем — до конечного значения — на рабочих лопатках, что обусловливается соответствующим профилем проточной части.
На лопатках, вследствие наличия перепада давлений, наряду с непосредственным ударным (активным) действием струи, появляется реактивная отдача, т.е. полная сила, действующая на лопатку, складывается из двух составляющих.
Для стационарных паровых турбин для привода турбогенераторов можно выделить шесть типов:
— конденсационные без регулируемых отборов пара (К-300-240);
— конденсационные с двумя регулируемыми отборами пара (производственным и теплофикационным, ПТ-135/165-130/13);
— конденсационные с производственным регулируемым отбором пара (П-6-35/5);
— конденсационные с теплофикационным регулируемым отбором пара
(Т-250/300-240);
— противодавлением без регулируемых отборов пара (Р-100-130/15);
— противодавлением и с производственным регулируемым отбором пара (ПР-25/30-90/10/0,9).
Произвольная классификация паровых турбин может быть:
— по числу ступеней ;
— по направлению потока рабочего тела;
— по числу корпусов ;
— по принципу парораспределения ;
— по принципу действия пара ;
— по характеру теплового процесса ;
— по параметрам свежего пара ;
— по использованию в промышленности ;
— по источнику энергии ;
— по роду рабочего тела ;
— по выполнению проточной части ;
— по выполнению регулирующей ступени ;
— по количеству валов ;
— по числу оборотов ;
— по числу потоков рабочего тела;
— по числу выхлопов и т. д.
1.4 История развития турбомашин
Попытки создать турбинный двигатель, предпринимались во многих промышленно развитых странах. Так, за первые две трети XIX века было сделано свыше 200 предложений на постройку паровых турбин.
В 1806 г. П.М.Залесов на Алтайском Сузунском заводе разработал конструкцию активной паровой турбины и в 1807 г. построил ее. Однако, по ряду причин теоретического и технологического плана, паровая турбина получила практическое применение лишь в самом конце XIX века. Последовательно, в этот период, развитие паровой турбины происходило следующим образом.
В 1856-1857 г.г. В. П. Титов в Петербурге построил и испытал сконструированную им паровую турбину реактивного типа. В 1884 г. англичанин Ч. Парсонс патентует паровую реактивную многоступенчатую турбину. В 1889 г. шведский инженер Густав Лаваль получает в Англии патент на расширяющееся сопло, т. е. изобретает сверхзвуковую турбину активного типа. В 1891 г. турбина снабжается конденсатором и появляется турбинный двигатель. В 1897 г. русский инженер морского флота П. Д. Кузьминский спроектировал и построил первый ГТД с процессом горения при постоянном давлении. В 1900 г. инженер Рато (Франция) разработал конструкцию активной турбины с несколькими ступенями давления и инженер Целли (Швейцария) ее усовершенствовал за счет регенерации.
Первые турбины имели мощность 3-5 л.с., но к 1900 г. их мощность доходила уже до 300 — 500 л.с. Пар использовался насыщенный при давлении до 10 кгс/см 2 с выпуском в конденсатор с глубоким вакуумом.
Первая турбина в России в 1907 году и имела мощность 200 кВт. Турбина была конденсационная с начальным давлением пара 10 кгс/см 2 и температурой 250 °С.
В развитии Российского турбостроения внесли вклад инженеры
Лосев С.М., Шляхин П. Н., Кириллов И. И., Щегляев А. А., Звягинцев В. В., Жирицкий Г. С., Смоленский А. Н., Яновский М. И. и другие.
Турбостроительные заводы: ПО ЛМЗ, ПО Атомтурбостроение ХТЗ, НЗЛ, ТМЗ и КТЗ.
Исследовательские и проектные институты: ВТИ, ЭНИН, ЦКТИ имени И. И. Ползунова, ЦНИИ им. А. Н. Крылова, ЦНИИТмаш, МГТУ, МАИ, ЛПИ, ЦИАМ и другие.
1.5 Устройство турбомашин
Турбина — ротативный тепловой двигатель с непрерывным процессом преобразования тепловой энергии рабочего вещества в механическую работу. Кинематическая схема её предельно проста.
Турбина состоит из двух основных узлов: вращающаяся часть — ротор, и неподвижная часть — корпус (статор).
К корпусу (статору) турбины относят:
— собственно корпус, который необходим для закрепления неподвижных элементов и организации потока рабочего тела от паровпуска через проточную часть до выпускного патрубка;
— сопловые лопатки – служат для разгона и формирования потока;
— направляющие лопатки – применяются для направления потока на рабочие лопатки;
— диафрагма – предназначена для закрепления лопаток и разделения объема корпуса на отсеки постоянного давления;
— опорные подшипники – воспринимают радиальные нагрузки и дают возможность центровки элементов ротора и статора при сборке турбины;
— упорные подшипники – воспринимают осевую нагрузку от рабочего тела, действующего на рабочие лопатки, диски и уступы ротора; позволяют устанавливать осевые зазоры; являются фикс-пунктом, относительно которого происходит тепловое расширение ротора относительно статора;
— уплотнения – служат для ограничения утечек от протечек рабочего тела, либо предотвращают присос воздуха из атмосферы;
— тепловая изоляция – ограничивает потери тепла;
— выпускной патрубок – необходим для организованного движения отработавшего в турбине рабочего тела с минимальными потерями.
К ротору турбины относят:
— рабочие лопатки – предназначены для преобразования кинетической энергии рабочего тела в механическую работу вращения ротора;
— диск – служит для закрепления рабочих лопаток и передачи крутящего момента от рабочих лопаток к валу;
— вал – необходим для крепления дисков с лопатками и суммирования крутящих моментов ступеней;
Основным условием работы турбины является наличие разности давлений – перед сопловым аппаратом и за рабочими лопатками.
Сопла, совместно с рабочими лопатками, образуют проточную часть турбины (рисунок 1). В проточной части происходит двойное преобразование энергии рабочего вещества:
— в соплах потенциальная энергия пара или газа превращается в кинетическую; на выходе из сопел скорость потока составляет сотни метров в секунду;

Лекция 2. Уравнения потока рабочего тела в турбомашинах
— уравнения: скорости звука, неразрывности, сохранения импульса, сохранения энергии, расхода через сопло (щель), скорости рабочего тела, энтальпии в потоке, состояния, расхода в турбине; Л.Эйлера; Н.Е.Жуковского [2, 6, 7].
— применение фундаментальных уравнений термодинамики потока и газодинамики для стационарных условий в лопаточных машинах.
2.1 Уравнение скорости звука
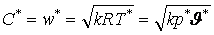
где 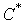
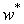
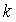
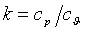

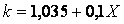
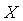
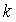
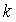

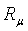
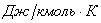
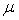
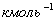
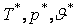
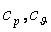
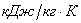
Режимы течения характеризуются числом Маевского (Маха)
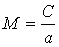

Для звукового критического истечения 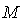
2.2 Уравнение неразрывности
Для адиабатически изолированного канала и неизоэнтропических процессов вдоль линии Фанно расход вещества 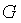
где 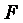
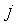
2.3 Уравнение сохранения импульса
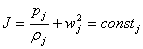
Линии постоянного импульса называют линиями Релея.
Линии Релея и линии Фанно совпадают в около звуковой области.
2.4 Уравнение сохранения энергии
где 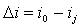
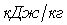


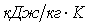
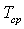
“0” – отвечает неподвижному (заторможенному) состоянию рабочего тела.
2.5 Уравнение расхода рабочего тела через сопло (щель)
где 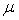
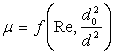

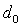
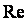
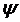
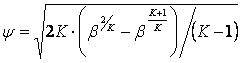
Для критического сечения (

Для трех- и многоатомных газов 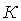

Для влажного пара 
2.6 Уравнение скорости пара (газа)
Для канала, окруженного адиабатической изоляцией
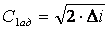
где 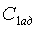
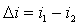


где 
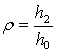

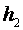
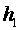
2.7 Уравнение энтальпии рабочего тела
где 
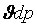

В процессе энергообмена между избранной данной системой и внешней средой система (турбомашина) приобретает третью степень свободы. Для турбин эти потери будем называть потерями с выходной скоростью, которые возникают из-за необратимости процессов в тепловом двигателе. Рост энтропии будет происходить за счет внутреннего тепловыделения от трения. Потери энергии (диссипация энергии) проявляются в виде нагрева болтов, шпилек, фланцев, фундамента машины.
2.8 Уравнение расхода рабочего тела
Общее уравнение преобразования энергии в турбине типа К и Р без учета регенеративного отбора пара:
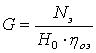
где 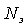

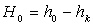


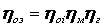
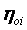
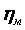
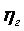
Для одиночной ступени турбины
где 
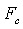

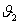
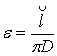
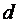
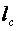

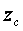
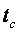
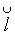
2.9 Уравнение Л. Эйлера
Окружное усилие равно
где 
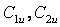
β 1 , β 2 – углы входа и выхода при относительном движении;
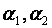
Знак “+” при 

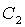
Уравнение, определяющее величину 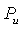
2.10 Теорема Н. Е. Жуковского
Она определяет подъемную силу лопатки У единичной длины


где 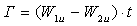

Либо величина Г определяется как
где 
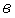
Знак “+” – для турбинного уравнения, а знак “-” – для насосного уравнения.
Лекция 3. Относительный лопаточный к.п.д. ступени турбины
— активная и реактивная одновенечные ступени турбины, их к.п.д., степень реакции колеса, баланс потерь энергии, потери энергии в лопатках и с выходной скоростью [2, 7, 8].
— проведение расчетов к.п.д. ступени и потерь в ступени, анализ физических явлений и процессов, разработка мероприятий по снижению потерь энергии.
3.1 К.п.д. активной одновенечной ступени турбины
Считаем, что

где 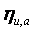
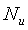


Запишем 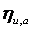
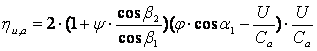
где 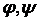
Наивыгоднейшее значение имеет вид

Тогда максимальное значение имеет вид
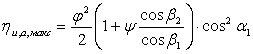
Таким образом, для получения максимального к.п.д. необходимо минимизировать потери 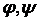
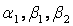
3.2 К.п.д. реактивной одновенечной ступени турбины
Считаем, что 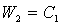

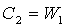

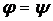

Сравнение с к.п.д. активной машины показывает 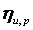
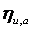
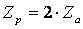
3.3 Степень реактивности
Она возрастает от корня лопатки к вершине. У корня предусматривается всегда небольшая положительная реакция, которая обеспечивает конфузорное течение рабочего тела и тем самым исключает подсосы пара. В первых ступенях машин применяют 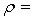


Однако наличие 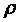
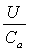
В целом, наличие 
3.4 Баланс потерь энергии одновенечной ступени турбины
К.п.д. через тепловые потери имеет вид
где 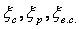
3.5 Потери энергии в соплах
Они возникают за счет:
— трения о стенки;
— отрыва пограничного слоя;
— вихревых дорожек в кромочном следе;
— концевых явлений у торцевых стенок;
Полный коэффициент потери энергии в сопловой решетке равен сумме коэффициентов профильных и концевых потерь:
Соответственно, для сопловых решеток, составленных из стандартных профилей с хорошо обработанными поверхностями
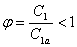
меньшее значение – для сопловых каналов очень малой высоты.
Потери энергии в соплах

Для снижения 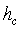
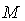
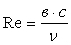
3.6 Потери энергии в рабочих лопатках
Они аналогичны потерям в соплах, к которым добавляются:
— потери через зазор;
— потери от перекрыши.
Потери через зазор дают подсос или протечку рабочего тела, вызывающие потери энергии. Поэтому применяют уплотнения зазоров (корневые и бандажные) и вводят реакцию лопатке.
Потери от перекрыши 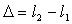
Поэтому оптимизируют величины перекрыш
причем меньшая величина применяется для
Полный коэффициент потери энергии на рабочей решетке:

Потери энергии на рабочих лопатках
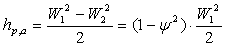
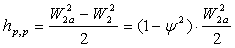
где 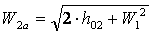
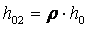
3.7 Потери энергии с выходной скоростью в решетке
Они возникают за счет скорости
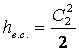
т.е. повышается энтальпия отработавшего пара.
Для турбины, в целом, эти потери велики:
— турбины типа К – (1÷ 2)% от 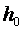

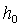
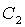
— турбины типа Р –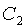
Для снижения потерь 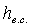
Лекция 4. Геометрические и конструктивные характеристики и параметры лопаточных решеток
— профиль лопаток, его характеристики, типы решеток, основные размеры решеток, число и установка лопаток [2, 6, 7, 12].
— построение профиля лопаток, определение его геометрических, конструктивных и газодинамических параметров, выбор типа решеток и установка профилей.
4.1 Геометрические характеристики профилей
К геометрическим характеристикам относятся:
— 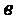
— 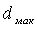

— 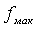

— 
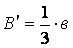
— 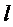
— 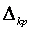
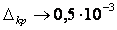
— 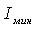
— 
— 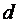
— 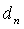
— 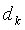
4.2 Геометрические параметры
— 
— 
— 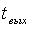
— 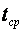
— 
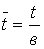
— 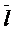

— 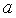
— 
— 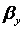
— 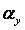
— 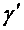
— 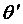
4.3 Газодинамические параметры
— 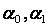
— 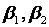
— 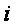
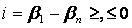
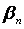

— 
4.4 Газодинамические характеристики
— 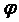
— 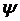
— 
— 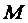
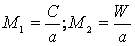
— 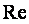
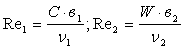
4.5 Конструктивные параметры
— 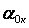
— 
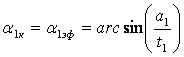
— 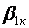
— 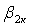
— 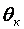
4.6 Типы решеток
Решетки имеют определенную форму межлопаточных каналов, каждой из которых соответствует свой тип решетки:
— A – дозвуковые решетки ;
— Б – околозвуковые ;
— В – сверхзвуковые ;
— И – с изломом профиля;
— М — широкий диапазон.
Обозначение: C -90-12Б – сопловая решетка, 

Для выбора типа решеток используют нормализованные профили ЛМЗ, ЦКТИ, МЭИ и др. Выбор ведут по атласу профилей решеток (нормали профилей).
4.7 Определение высоты лопаток
Из уравнения неразрывности для выходного сечения сопел:
Для регулирующей ступени из условий экономичности и прочности
Степень парциальности 
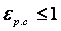
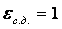
Для коротких лопаток
где
для длинных лопаток
где
4.8 Число и ширина лопаток
Для сопловой решетки


Для рабочих решеток


Ширина лопаток 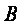

где 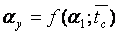
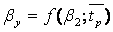
Лекция 5. Внутренний относительный к.п.д. турбинной ступени
— потери на дисковое трение и парциальный подвод, потери от утечек в лабиринтовых уплотнениях, потери от влажности пара, эрозия рабочих лопаток и методы борьбы с ней, к.п.д. ступени турбины [2, 7, 8, 12].
— определение дополнительных потерь на трение, парциальный подвод, от утечек и от влажности пара, организация технических мероприятий по снижению этих потерь, пути преодоления эрозии рабочих лопаток, расчет эффективности ступени с учетом дополнительных потерь.
5.1 Потери на дисковое трение и вентиляцию (парциальный подвод)
Потери на трение и вентиляцию, от утечек и влажности называют дополнительными по отношению к потерям в соплах, на рабочей решетке и с выходной скоростью. Поэтому все эти суммарные шесть потерь определяют внутренний относительный к.п.д. ступени турбины.
На преодоление трения вращающегося диска затрачивается механическая работа. Она превращается в тепло и повышает энтальпию пара.
При парциальном подводе пара на длине дуги, не занятой соплами, происходит вихревое движение пара в каналах рабочих лопаток. Это вихревое движение вызывает вентиляционную (вентиляторную) потерю, т.е. колесо работает как вентилятор: трение и удар рабочего тела о рабочие лопатки; вентиляторное действие лопаток вместо турбинного; прерывистое поступление рабочего тела, вызывающее периодическую нестационарность рабочего тела в межвенцовом зазоре и на рабочих лопатках.
Также при парциальном подводе возникает потеря на “выколачивание” (“выталкивание”) рабочего тела. Каналы рабочих лопаток заполнены движущимся паром только тогда, когда они находятся напротив сопел. Все остальные каналы заполнены застойным паром. При подходе этих каналов к соплам пару требуется затратить часть своей энергии на выталкивание застойного пара и его ускорение.
На преодоление этих вредных сопротивлений затрачивается механическая работа, она переходит в тепло и вызывает повышение энтальпии пара.
Проводившиеся исследования показали, что потери энергии на трение и вентиляцию возрастают при увеличении: плотности среды, в которой вращается диск; среднего диаметра ступени; длины рабочих лопаток; окружной скорости ступени; при уменьшении степени парциальности впуска e .
Потери на вентиляцию уменьшаются с уменьшением зазора между корпусом турбины и рядом рабочих лопаток. Для уменьшения этого зазора вдоль нерабочей части колеса делаются прикрывающие щитки, позволяющие уменьшить мощность, теряемую на вентиляцию в 2 ¸ 3 раза.
Для определения мощности, теряемой на трение и вентиляцию, предложено довольно много различных формул. Наиболее универсальная из них – эмпирическая формула Стодола, учитывающая сразу потери на трение диска и на вентиляцию рабочих лопаток:
где 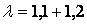
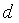
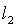



Потеря на трение и вентиляцию имеет существенное значение в малых турбинах (при небольших расходах пара G ), а также на первых ступенях турбоагрегатов с высоким начальным давлением пара. В ступенях мощных паротурбинных агрегатов эта потеря, как правило, мала. Особенно это относится к последним ступеням.
5.2 Потери от утечек в ступени
где 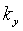
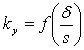
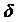
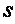

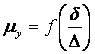



Тепловые диафрагменные потери
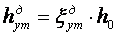
Кроме утечек через диафрагменные уплотнения существуют утечки через радиальные зазоры между статором и рабочими лопатками.
Потери в радиальных зазорах пропорциональны разности давлений на лопаточном венце, величине зазора и становятся ощутимыми при степени реакции r > 0,2.
Физический смысл потери состоит в том, что пар (газ), проходящий через щель, дросселируется, сохраняя свою энтальпию, т.е., часть энергии потока недоиспользуется.

где a = 3 ¸ 4,5 при r =0,25 ¸ 0,5.
5.3 Потери от влажности пара
Они имеют место в турбинах типа К на последних ступенях, в турбинах АЭС и др. Капли, образующиеся при конденсации пара, под действием центробежных сил отбрасываются к периферии, а также им сообщается ускорение от частиц пара основного потока. На это расходуется энергия.
Потери от влажности равны
где 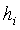
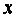
5.4 Эрозия рабочих лопаток и меры борьбы с ней
От ударов капель воды происходит эрозия (разъедание) лопаток. Она будет тем больше, чем меньше скорость капель воды, больше их диаметр и выше окружная скорость. Сила удара капли о лопатку пропорциональна квадрату окружной скорости. Крупные капли отбрасываются центробежными силами к периферии, и поэтому эрозии подвергается только (1/3 ÷ 1/2) часть лопатки. У корневой части эрозии нет. В средней части лопатки наблюдается эрозия в виде матового налета, далее – точечная и, наконец, – пористая эрозия. В процессе работы лопаток происходит замедление эрозии, т.к. в порах металла имеются частицы влаги, смягчающие удар капель воды.
Таким образом, факторы, уменьшающие к.п.д. ступени при наличие влаги:
— переохлаждение пара при расширении;
— тормозящее воздействие капель;
— ускорение капель потока;
— скачкообразное выделение влаги;
— уменьшение расхода пара при конденсации;
— отклонение параметров пара от расчетных;
— увеличение шероховатости рабочих лопаток от эрозии.
Для борьбы с эрозией применяют промперегрев и внешнюю сепарацию; создают каплеуловители с системами влагоудаления; защищают выходные кромки износоустойчивым твердым сплавом (стеллитом); используют капиллярнопористые материалы 17.
5.5 Внутренний относительный к.п.д. ступени
Он определяется выражением
где 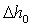
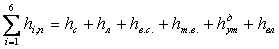
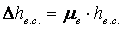

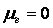
Лекция 6. Многоступенчатые турбины.
— преимущества и недостатки многоступенчатых турбин, к.п.д. турбины и ПТУ, коэффициент возврата тепла; предельное значение мощности, тепловой баланс турбины и пути обобщения опытных данных [2, 7, 8].
— раскрыть достоинства и недостатки многоступенчатых турбин, рассчитать к.п.д. турбины и ПТУ, коэффициент возврата тепла, оценить предельное значение мощности турбины, обобщить эксперимент характеристическими коэффициентами.
6.1 Преимущества и недостатки многоступенчатых турбин
Многоступенчатые турбины строятся на большие мощности и высокие сверхкритические параметры пара. Число ступеней может достигать 30 и более, которое зависит от начальных и конечных параметров рабочего тела, его расхода, типа регулирующей ступени, ожидаемой надежности, экономичности и маневренности.
В современных паровых турбинах реализуется теплопадение до 1600 
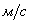

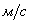
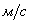
В многоступенчатых турбинах есть возможность перераспределить теплоперепад между регулирующей ступенью (до 250 
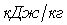

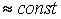
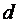
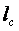
При большом количестве Z решается проблема использования выходной скорости, т.к. к последующей ступени добавится кинетическая энергия предыдущей. Более того, появляется возможность отбора пара на регенерацию, что увеличит к.п.д. ПТУ. Однако к.п.д. самой турбины ухудшается и усложняется ее конструкция.
Другим преимуществом многоступенчатых турбин является частичная утилизация тепловых потерь предыдущих ступеней.
К недостаткам таких турбин можно отнести: большие габариты, сложная конструкция, технология изготовления, усложняется эксплуатация, сборка, монтаж, ремонт.
Применение многоступенчатых турбин приводит к повышению их к.п.д. по следующим причинам:
1. В каждой ступени может быть выдержано наивыгоднейшее значение характеристики х1, обеспечивающее получение максимального окружного КПД.
2. Небольшие теплоперепады в каждой ступени позволяют применять сходящиеся сопла, имеющие меньшие потери, более простые в технологическом отношении и работающие устойчиво на переменных режимах.
3. Выходная скорость из каждой ступени (кроме последней) не является потерянной, а может быть использована в последующей ступени, повышая тем самым общий к.п.д. турбины.
4. Наличие потерь энергии в данной ступени частично компенсируется увеличением действительных располагаемых теплоперепадов следующих ступеней за счет «возвращенного тепла», что также повышает общий к.п.д. турбины.
6.2 К.п.д. турбины и ПТУ (“парадные” показатели)
Относительный внутренний к.п.д. турбины

где 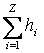
Теоретическая мощность турбины
Внутренняя мощность турбины
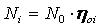
Эффективная мощность турбины

где 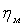
Мощность на клеммах электрогенератора
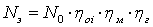
где 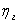
Абсолютный внутренний к.п.д.
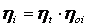
где 
К.п.д. турбины различен для ее цилиндров. Он составляет для ЦВД 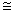
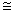
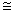
Удельный расход пара
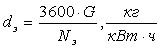
Величина 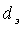
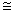

Механический КПД 
Относительный эффективный КПД 
Абсолютный эффективный КПД 
КПД электрогенератора 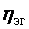
Относительный электрический КПД 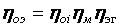
Абсолютный электрический КПД 
КПД паросиловой установки в целом 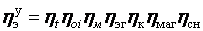
где 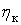
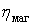
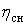
Наивысшие значения КПД, достигнутые в опытно-промышленных установках при наличии промперегрева пара и развитой регенеративной системе подогрева питательной воды:
Япония N э = 700 МВт, P 0 = 31 МПа, t 0 = 566 ° С, 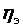
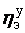
США N э = 500 МВт, P 0 = 35 МПа, t 0 = 650 ° С, 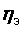
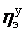
6.3 Коэффициент возврата тепла
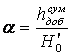
где 
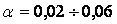

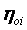
6.4 Характеристические коэффициенты
который дает
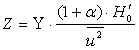
где 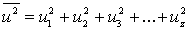
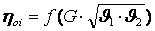
где 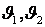
Таким образом, приведенные коэффициенты позволяют обобщать опытные данные в турбинах, и по графикам определять величины z и к.п.д. турбин.
6.6 Предельная мощность турбин
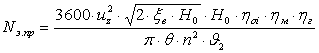
где 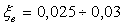


Величина 
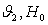
Для достижения максимальной мощности турбин:
— раздваивают потоки пара в последних цилиндрах;
— организуют многопоточные способы канализации пара в ЦСД;
— конструируют двухъярусные ступени;
— организуют регенерацию пара;
— применяют титановые сплавы и тихоходные турбины.
Лекция 7. Конструкция современных паровых турбин
— выбор регулирующей ступени, законы изменения корневого диаметра, выбор числа оборотов, числа цилиндров [2, 7, 14, 15, 18].
— осуществление выбора основных конструктивных схем турбомашины.
7.1 Выбор регулирующей ступени
Устанавливают одно- или многовенечные ступени. Одновенечная ступень перерабатывает теплоперепад до 120 кДж/кг, принимая тепловой и газодинамический удар рабочего тела. Двухвенечная ступень может воспринять до 250 кДж/кг, но не более 30 % от идеального теплопадения турбины (рисунок 2).

При уменьшении к.п.д. двухвенечной ступени на 1 %, к.п.д. турбины снижается на 0,3 – 0,7 %.
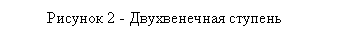
При мощности более 100 МВт давление за регулирующей ступенью по-прежнему высокое, и поэтому всегда устанавливают одновенечную ступень.
Двухвенечные ступени облегчают проведение переменных режимов работы для турбин малой и средней мощности.
7.2 Выбор закона изменения корневого диаметра
Он формирует проточную часть турбины. Для турбин с N ≤ 100 МВт выбирают постоянным корневой диаметр, что удешевляет турбину.
Для больших мощностей для ЦНД снижают корневой диаметр по потоку пара, что улучшает обтекание корневой зоны. Однако невозможно унифицировать хвостовики лопаток и дисков.
Для ЦВД крупных турбин корневой диаметр возрастает по проточной части, что позволяет увеличить высоту лопаток первых ступеней и повысить их к.п.д..
7.3 Выбор числа оборотов
Число оборотов n > 3000 об/мин имеет место для турбин малой мощности, которые используются в качестве привода нагнетателей. Предельная мощность в одном цилиндре не более 12 – 35 МВт; очень дорогой редуктор.
Величина n = 1500 об/мин позволяет повысить экономичность ЦНД. Если число потоков ЦНД уменьшить в 4 раза, то в 16 раз уменьшатся потери с выходной скоростью. Однако экономичность ЦВД снизится, т.к. будут меньше длины лопаток. Поэтому 1500 об/мин применяют на АЭС большой мощности (N≥500 МВт), когда ЦВД – двухпоточный и вырабатывает более 30 % общей мощности. Более того, повышается надежность, уменьшаются растягивающие и изгибные моменты, возрастает резонансная кратность и вибрационная надежность лопаток, снижается эрозия, уменьшается вероятность проявления податливости опор и упругости масляной пленки в подшипниках. Стоимость же турбины возрастает, т.к. масса ротора увеличивается в 2 раза, а корпуса – в 1,3 раза по сравнению с турбинами, работающими на 3000 об/мин.
7.4 Выбор числа валопроводов
Исторически изготовляли 2 вала, т.к. не было электрогенераторов большой мощности. Опыт эксплуатации выявил технические трудности по изготовлению, монтажу и эксплуатации. Однако определились достоинства: ремонтопригодность. Экономичность – одинаковая, стоимость – большая. Двухвальная турбина может быть целесообразна, если N>(2000 – 3000) МВт, когда вал ЦВД и ЦСД вращается с f = 50 c -1 , а ЦНД – с f = 25 c -1 .
7.5 Выбор числа цилиндров
Он определяется предельной мощностью турбины, наличием промперегрева и регенерации. Экономичность при этом возрастает как ПТУ, так и агрегата, т.к. снижаются потери с выходной скоростью, влажность и возрастает высота лопаток. Однако снижаются надежность и маневренность, возрастает податливость опор.
Отечественные машины мощностью до 50 МВт изготавливают одноцилиндровые, либо при спецмерах, ухудшающих экономичность, до 100 – 150 МВт (полупиковые машины). Например, К-100-130 имеет 2 цилиндра и z=18 ступеней, К-200-130 – 3 цилиндра и z=27 ступень, К-300-240-3 цилиндра и z=34, К-500-240 — 4 цилиндра и z=31 и К-1200-240 — 5 цилиндров и z=31 ступень.
Лекция 8 . Потери энергии вне проточной части
— Классификация потерь в турбине. Потери в клапанах. Механические потери. Потери в выпускном патрубке и паропроводах. Лабиринтные уплотнения турбомашин: конструктивные схемы, принцип работы и расчет.
[ 5.2 ] — §§ 5.1; 5.3; гл. 11; [ 5.8 ] — §§ 6.4 — 6.9; [ 5.9 ]
— расчет потерь энергии рабочего тела вне проточной части.
8.1 Классификация потерь в турбине
Природу всех потерь можно считать тепловой, т.е. энтропия растет за счет внутреннего тепловыделения от трения. Общая величина потерь
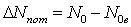
или 
Все потери разделим на 2 группы:
— внутренние, влияющие на изменение состояния рабочего тела в турбине (потери в клапанах, соплах и т.д.);
— внешние, не влияющие на изменение этого состояния ( от утечек в концевых лабиринтах, в штоках клапанов, механические и др.).
8.2 Потери в клапанах
Потеря давления от дросселирования

Располагаемый теплоперепад снижается на величину
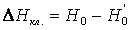
Конструктивно клапаны классифицируют на:
Типы регулирующих клапанов:
-обтекаемый односедельный с коническим диффузором;
-объединенный (стопорный с регулирующим).
8.3 Механические потери
Они связаны с затратой энергии на преодоление сопротивления в подшипниках турбины, генератора, возбудителя и др., на привод системы регулирования и главного масляного насоса системы маслоснабжения. Потери определяются опытом, зависят от мощности и составляют ≈1 %.
8.4 Потери в выхлопном патрубке, теплообменниках и паропроводах
Они связанны с потерей кинетической энергии, с которой отработавшее рабочее тело покидает проточную часть турбины
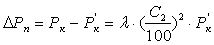
где Р к и Р к ‘ – давление пара за колесом и в выпускном патрубке;
λ- коэффициент, зависящий от конструкции патрубка,
λ=0,07 – 0,1 с 2 /м 2 .
Скорость С 2 для турбин типа Р равна (40÷60) м/с,
а типа К — 80÷120 м/с (иногда до 200÷300 м/с).
Потери ΔР n уменьшают энтальпию отработавшего пара и полезно использованное тепло.
В современных конструкциях патрубки выполняют диффузного типа, что обеспечивает частичное восстановление давления и скорость С 2 преобразуется в давление.
Потери давления в промперегревателе

Потери давления в перепускных паропроводах
8.5 Утечки в уплотнениях штоков клапанов
Они приводят к потерям пара и дискомфорту в машзале. Утечки возникают вследствие протечки пара через зазор между втулкой (буксой) и шпинделем (штоком) клапана. Эта проблема, истечение через длинные узкие щели, является нерешённой, т.к. не выяснено влияние выточек и неконцентричности расположения шпинделя во втулке.
Утечки определяются формулой
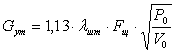
где λ шт – коэффициент, зависящий от трения, длины щели и радиального зазора между штоком и втулкой δ, определяется по графику;
Fщ – площадь щели

d шт – диаметр штока;
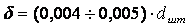
Р 0 , V 0 – давление и удельный объем пара перед щелью, бар и м 3 /кг.
При росте эксцентричности величина G ут возрастет на (50÷100)%. При наличии выточек G ут сокращается на (5÷15)%.
8.6 Лабиринтные уплотнения турбомашин: конструктивные схемы, принцип работы и расчет.
В местах выхода вала из корпуса турбины устанавливаются концевые уплотнения. В областях высоких давлений уплотнения ограничивают выход пара из турбины, а в областях, находящихся под давлением ниже атмосферного, препятствуют подсосу атмосферного воздуха в турбину и конденсатор, обеспечивая их нормальную работу.
В современных турбомашинах применяются почти исключительно металлические лабиринтовые уплотнения ввиду их относительной эффективности и надежности в работе. Они служат для ограничения протечек пара помимо проточной части турбины через радиальные и осевые зазоры между поверхностями статора и ротора машины. Конструктивно лабиринты представляют собой ряд последовательно расположенных друг за другом кольцевых щелей (зазоров) и достаточно просторных полостей (камер). Зазоры между ротором и статором образуются их поверхностями и заостренными кромками гребней, отделяющих камеры друг от друга. При прохождении рабочего тела через зазор под гребнем уплотнения потенциальная энергия его преобразуется в кинетическую энергию струи, которая, в свою очередь, гасится в камере и превращается в тепловую. Таким образом, в ячейке лабиринта имеет место термодинамический процесс — адиабатное дросселирование. Этот процесс повторяется от ячейки к ячейке, в результате чего, давление рабочего тела вдоль лабиринта падает, удельный объем, скорость потока и перепад давлений на гребень возрастают, чем и создается уплотнительный эффект.
Поскольку уплотнения относятся к одному из важнейших узлов турбомашин, существенно влияющих на экономичность и надежность последних, то к ним предъявляют целый комплекс разнообразных требований, основными из которых являются:
1. Конструкции гребня и следующей за ним камеры должны быть выполнены так, чтобы в камере по возможности полностью гасилась кинетическая энергия, приобретенная паром при протекании через узкое сечение зазора. Если это условие не будет соблюдено, то расход пара через уплотнение увеличивается.
2. Расположение гребней лабиринтов должно быть компактным с тем, чтобы в пределах заданной длины вала разместить наибольшее количество гребней; при этом, однако, не следует допускать слишком малые размеры расширительных камер, так как в этом случае в них не будет полностью гаситься кинетическая энергия.
3. Конструкция уплотнения должна быть выполнена так, чтобы малые зазоры между неподвижными гребнями и ротором турбины не могли быть причиной аварии турбины.
4. Конструкция уплотнения должна быть проста в изготовлении, монтаже, ремонте, долговечна и безотказна в работе.
Сочетать в одной конструкции все эти требования очень сложно, поэтому в настоящее время существует большое количество типоразмеров уплотнений.
По направлению движения среды относительно оси вращения ротора, уплотнения делятся на осевые, радиальные, диагональные. По геометрическому признаку, т.е. по ориентации уплотнительного зазора, уплотнения бывают с радиальными зазорами, с осевыми зазорами и комбинированные.
Лекция 9. Схемы и циклы газотурбинных установок
— конструктивные схемы газовых турбин, цикл простейшей ГТУ, цикл ГТУ с регенерацией, тепловой расчет газовой турбины с регенерацией тепла уходящих газов. Повышение эффективности циклов ГТУ.
— ознакомление с конструктивными схемами газовых турбомашин, способами повышения экономичности ГТУ.
9.1 Общие сведения

Развиваемая газовой турбиной мощность частично расходуется на привод компрессора, а оставшаяся часть является полезной мощностью газотурбинной установки. В отличии от ПТУ полезная мощность ГТУ составляет только 30-50 % от мощности турбины. Эффективность ГТУ в сравнении с другими тепловыми двигателями обнаруживается только при очень высокой температуре газов, поэтому ГТУ стали применять значительно позже других тепловых двигателей.
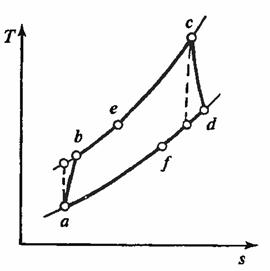
9.2 Цикл простейшей ГТУ
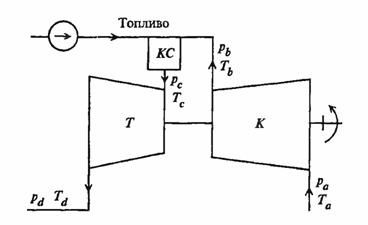
Основные характеристики цикла и установки:
Степень сжатия в компрессоре (степень расширения в турбине)
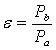
Отношение абсолютных значений граничных температур
Удельная полезная работа ГТУ
Работа турбины и работа компрессора
Удельная подведенная теплота
Технико-экономические показатели газотурбинных установок простейшей схемы невысоки и, естественно, зависят от температуры газа перед турбиной: абсолютный электрический КПД на уровне 20-24 %, коэффициент полезной работы порядка 0,25-0,28 (т.е. большая доля мощности, развиваемой турбиной, приходится на привод компрессора), а удельный расход газа достигает
25-45 кг/кВт × ч.
Для улучшения технико-экономических характеристик газотурбинных установок предлагаются следующие пути:
1. Использование регенеративного цикла.
2. Приближение процесса сжатия воздуха в компрессоре к изотермическому.
3. Приближение процесса расширения газа в турбине к изотермическому.
9.3 Газотурбинная установка с регенерацией тепла
Эффективным средством повышения экономичности простой схемы газотурбинной установки, работающей по циклу со сгоранием топлива при постоянном давлении, является регенерация тепла, то есть использование в схеме тепла уходящих из турбины газов, которое безвозвратно теряется в установках, выполненных по простейшей схеме.
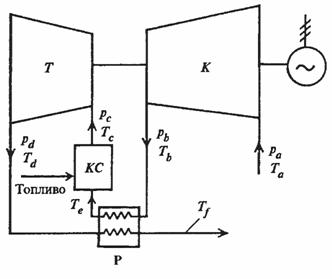
Воздух, сжатый в компрессоре, по пути следования в камеру сгорания проходит через регенератор (воздухоподогреватель), где подогревается за счет тепла отработавших газов, покидающих турбину с относительно высокой температурой.
Доля тепла уходящих газов, отданная воздуху в регенераторе называется «степенью регенерации».
Степенью регенерации называется отношение количества тепла, фактически воспринятого воздухом в регенераторе при нагреве до Те, к тому количеству тепла, которое воздух воспринял бы, нагреваясь до максимально возможной температуры Т d (температуры газа на выходе из турбины).

Внутренний КПД газотурбинной установки, работающей по простейшей схеме при наличии регенератора:
Анализ формулы для определения h показывает, что КПД действительного цикла существенным образом зависит от степени регенерации. Кроме того, с повышением s (при прочих равных условиях) одновременно с ростом КПД газотурбинной установки уменьшается значение наивыгоднейшей степени сжатия в компрессоре.
Последнее обстоятельство позволяет в газотурбинных установках с регенерацией уменьшить затраты мощности на привод компрессора, одновременно уменьшив размеры компрессоров, то есть приводит к сокращению габаритов механической части ГТУ. Однако, несмотря на это, общие габариты установки увеличиваются вследствие появления в схеме громоздкого регенератора.
9.4 Повышение эффективности циклов ГТУ.
Из курса технической термодинамики известно, что работа сжатия газа будет наименьшей, если сжатие осуществляется изотермически. При этом в процессе сжатия должен осуществляться интенсивный отвод тепла. Максимальная работа расширения газа имеет место при изотермическом процессе, для обеспечения которого в процессе расширения требуется подвод тепла.
В реальных условиях возможны два пути приближения процесса сжатия воздуха в компрессоре к изотермическому: влажное сжатие, ступенчатое сжатие с промежуточным охлаждением. Осуществить изотермическое расширение конструктивно весьма затруднительно. Наиболее простой путь для приближения к идеальному процессу – промежуточный подвод тепла при ступенчатом расширении газа в нескольких последовательно расположенных турбинных корпусах, между которыми располагаются промежуточные камеры горения. Практически реализуемые схемы имеют как правило одну ступень промежуточного охлаждения при сжатии и одну ступень промежуточного подвода теплоты при расширении (рисунок 8).
В таблице 1 приведены сравнительные расчетные данные основных показателей работы газотурбинных установок различных схем.
Практические рекомендации по повышению эффективности работы газотурбинных установок:
— при мощностях до 5-6 МВТ – простая схема без регенератора или с регенератором;
-в установках средней мощности от 5-6 МВт до 18-20 МВт – увеличение экономичности за счет одного промежуточного охладителя и регенератора;
— применение одновременно промежуточных охладителей (до двух), одной промежуточной камеры горения и регенератора целесообразно только для газотурбинных установок большой мощности, начиная от 20 МВт и выше.
Видео:Закон БернуллиСкачать

Документы
ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ
9-1. ОСНОВНЫЕ УРАВНЕНИЯ
В ступени турбомашиньи происходит преобразование потенциальной энергии газа в механическую работу (турбина) или механической работы в потенциальную энергию газа (компрессор). В обоих случаях поток газа совершает энергетический обмен с окружающей средой.
Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.
Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турбины; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени 114 .
Введем в отличие от предыдущего следующие обозначения скоростей:
с — скорость абсолютного движения газа; скорость газа в относительном движении;
Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений и скоростей •в проточной части (б).
¦ скорость переносного движения (окружная скорость); и wи — проекции ско
ростей абсолютного и относительного потоков на направление скорости и;
— проекции скоростей абсолютного и относительного потоков на направление оси вращения;
.,w — радиальные составляющие скоростей абсолютного и относительного потоков.
Индексом 1 обозначим скорости, относящиеся ко
входу, a индек!сол^ 2 — к выходу из рабочих лопаток.
Рабочий процесс ступени турбины можно (проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью с, направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-6П2.2 Дейч Михаил Ефимович
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л.
с черт. и илл. 6П2.2
Редактор Б. Я¦ Шумяцкий Техн. редактор А. М. Фридкин
ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ
9-1. ОСНОВНЫЕ УРАВНЕНИЯ
В ступени турбомашиньи происходит преобразование потенциальной энергии газа в механическую работу (турбина) или механической работы в потенциальную энергию газа (компрессор). В обоих случаях поток газа совершает энергетический обмен с окружающей средой.
Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.
Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турби-ньи; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени 115 .
Введем в отличие от предыдущего следующие обозначения скоростей:
с — скорость абсолютного движения газа; w — скорость газа в относительном движении; и — скорость переносного движения (окружная скорость); проекции скоростей абсолютного и относительного потоков на направление скорости и;
Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений н скоростей ¦в проточной части (б).
проекции скоростей абсолютного и относительного потоков на направление оси вращения;
радиальные составляющие скоростей абсолютного и относительного потоков.
Индексом 1 обозначим скорости, относящиеся ко
входу, а индекйоА^ 2 — к выходу из рабочих лопаток.
Рабочий процесс ступени турбины можно проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью сь направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-генциальная энергия газа преобразуется в кинетическую энергию потока.
На рабочие лопатки поток входит с относительной скоростью wI, которую легко получить, ‘построив входной треугольник скоростей.
В межлопаточных каналах рабочей решетки происходи? поворот потока в относительном движении; при
Рис. 9-2. Развертка проточной части (а) и треугольники скоростей осевой ступени (б).
этом силы давления газа производят работу вращения ротора турбины. Поток выходит из рабочих лопаток с относительной скоростью w2 под углом Рг к оси решетки. Зная окружную скорость и, легко построить выходной треугольник скоростей и определить скорость абсолютного потока на выходе из ступени с2 (рис. 9-2,а). Часто входной и выходной треугольники скоростей изображают из одного полюса, как показано на рис. 9-2,6.
Таким образом, энергия газа передается к ротору турбины благодаря тому, что силы давления три повороте потока на лопатках производят работу вращения ротора. В результате температура и давление торможения абсолютного потока уменьшаются так, что
‘ Характерной особенностью рассмотренного процесса является его ступенчатый характер: потенциальная энергия вначале преобразуется 1 кинетическую энергию движущегося газа, а затем на рабочем колесе кинетическая энергия преобразуется в механическую работу. Такой процесс в чистом виде имеет место в активной ступени: статические давления на входе и выходе из рабочей решетки примерно одинаковы, а скорости Wi и W2 различаются только за счет потерь в рабочей решетке.
В чисто реактивной ступени оба составляющих процесса протекают одновременно на рабочем колесе. Поток газа в рабочих каналах в относительном движении ускоряется и одновременно совершает работу вращения ротора. Широкое применение находят промежуточные типы ступеней, в которых рационально сочетаются оба принципа — активный и реактивный. В этом случае преобразование потенциальной энергии газа в кинетическую осуществляется частично в неподвижной решетке и частично в рабочих каналах.
Изменение статических параметров потока и параметров торможения в проточной части такой ступени показано на рис. 9-1,1.
Ступень может быть выполнена также с радиальным потоком газа. В такой ступени газ движется в радиальных плоскостях от оси вращения к периферии или, наоборот, к оси вращения. Радиальная ступень может бьить активного, реактивного или промежуточного типа.
Схемы проточньих частей ступеней турбины с радиальным потоком газа показаны на ри,с. 9-3. В радиальном сечении видны формы профилей направляющей и рабочей решеток ступени и треугольники скоростей на входе и выходе из рабочих каналов. Заметим, что в радиальной ступени окружная скорость меняется от входного к выходному сечению решетки.
В некоторых ступенях поток газд направлен поя углом к оси вращения. При этом радиальные составляющие скорости сг не равны нулю и при анализе свойств потока должны учитываться (рис. 9-4).
В ступени компрессора (осевого или центробежного) происходит преобразование механической работы в по-
Рис. 9-3. Схемы центробежной (а) и центростремительной (б) радиальных ступеней турбины.
тенциальную энергию газа Каналы рабочей решетки 1 осевого компрессора — расширяющиеся^(рис. 9-5). Давление газа в относительном движении возрастает, а скорость уменьшается. Этот процесс продолжается в направляющем аппарате 2. Энтальпия полного торможения в абсолютном движении возрастает.
В ступени центробежного компрессора движение газа осуществляется от центра к периферии (рис 9-6), рабочие лопатки колеса 1 образуют расширяющиеся каналы, в которых происходит торможение относительного потока. Сжатие газа может продолжаться в лопаточном диффузоре 2.
В точной постановке задачи течение газа в ступени турбомашины описывается дифференциальными уравнениями пространственного потока — вязкой сжимаемой
»Рис 9-5. Схема и развертка проточной части ступени осевого компрессора.
жидкости. Приближенные решения основываются на уравнениях идеальной сжимаемой жидкости, выведенных в гл. 1.
Рис 9-4 Схема диагональной ступени.
движения, неразрывности и записать в цилиндрической качестве независимых переменных, как и ранее, выбираются: радиус-вектор г полярный угол 0 и аппликата г. Направление оси х совпадает с осью вращения турбины. Тогда система уравнений сохранения в абсолютном установившемся движении
(dpjdt = dcjdt = dcjdt= dcjdt = 0)
при R = e = Z = 0 сводится к уравнениям (1-14) и (1-17а).
Для исследования потока в рабочей решетке основные уравнения идеальной жидкости целесообразно записать для
относительного движения. При этбм используются очевидные соотношения (рис. 9-2):
W a = C a’ W r = C r И W u = C u
где ш — угловая скорость вращения рабочей решетки.
Рис 9-6 Схема ступени центробежного компрессора
После подстановки этих соотношений в уравнения (1-17а) для установившегося относительного движения получим:
Дифференциальное уравнение неразрывности для установившегося относительного потока имеет вид:
Система уравнений движения (1 — 17а) и (1-14) или (9-1) и (9-2) дополняется уравнениями сохранения энергии in изоэнтропического процесса При этом система уравнений, определяющая пространственное установившееся движение идеальной сжимаемой жидкости в ступени турбомашины, является замкнутой
Перейдем теперь к выводу уравнения энергии для струйки газа в проточной части ступени Уравнение энергии может быть записано в параметрах абсолютного или относительного движения В первом случае в уравнение энергии вводятся члены, учитывающие энергетический обмен между потоком и окружающей средой Во втором случае (для относительного потока) необходимо учитывать дополнительные силы, введение которьих позволяет рассматривать относительное движение, так, как если бьи оно было абсолютным Такими дополнительными силами являются кориолисова сила инерции и центробежная сила
Уравнение энергии для абсолютного потока напишем в форме первого начала термодинамики. С учетом сделанных допущений получим:
Здесь LT — работа, совершаемая газом.
Величина Lr может быть определена с помощью уравнения моментов количества движения. Момент сил, действующих на рабочие лопатки при установившемся движении, будет:
где G — секундный расход газа через решетку.
Умножив Ми на угловую скорость вращения решетки ш, найдем секундную работу или мощность, которой обмениваются лопатки с газовым потоком:
Следовательно, работа, отнесенная к весу протекающего газа, равна:
Уравнение (9-4) получено Эйлером. В дифференциальной форме уравнение Эйлера имеет вид:
Так как в турбине газ совершает работу, то вдоль струйки абсолютного течения d(cuu) 0. Использовав выражения (9-3) и (9-5), получим дифференциальное уравнение энергии для потока в абсолютном движении:
В соответствии с законом сохранения энергии изменение кинетической и внутренней энергии газа в относительном движении ,равно количеству подведенного («ли отведенного) тепла и работе действительных и дополнительных сил. Так как кориолисова сила инерции натравлена нормально к оси струйки в относительном движении (к вектору w), то работа этой силы равна нулю.
Таким образом, из числа дополнительных сил в уравнение анергии для потока газа в относительном движении необходимо ввести центробежную силу, направленную вдоль радиуса нормально к оси вращения. В частном случае аксиальной ступени вектор центробежной силы нормален к линиям тока и работа центробежных сил также равна нулю.
Уравнение энергии для потока в относительном движении получаем на основании первого начала термодинамики (9-3).
Учитывая, что = ст с*а— с и используя связь между абсолютными и относительными скоростями, преобразуем выражение (9-6). Получим:
Интегрирование уравнения энергии (9-6) для потока в абсолютном движении дает:
Интеграл уравнения энергии потока в относительном движении (9-7) равен:
Переход от уравнения (9-8) к уравнению (9-9), очевидно, совершается с помощью формулы (рис. 9-2,6)
Полученные уравнения для относительного движения могут быть использованы для расчета ступени не только турбины, но и других турбомашин (компрессор, вентилятор). Направление энергетического обмена (отвод или подвод механической работы) при этом не имеег значения. Это замечание вполне справедливо только в предположении изоэнтропического течения в ступени турбо-машиньв. В реальных условиях движение газа сопровождается потерями. При этом направление энергетического обмена существенно влияет на структуру потока (на характер распределения параметров в проточной части), а следовательно, и на к. п. д. ступени.
При отсутствии потерь изменение состояния газа в абсолютном и относительном движении подчиняется изоэнтропическому закону, который для идеального газа может бьпь представлен формулой p/p K =const.
В этом случае интегралы уравнений количества движения и энергии совпадают. Действительно, для одномерного потока в абсолютном движении уравнение импульсов имеет вид: ^
Считая относительное движение газа в ступени установившимся, запишем уравнение импульсов в такой форме:
wdw— по 2 cos (r,x) dx — 0,
где гш 2 cos (г х) dx — импульс центробежных сил.
Так как гш = и, то
Интегралы уравнений (9-11) и (9-12) совпадают с уравнениями (9-8) и (9-9), если di = dpjp, что соответствует изоэнтропическому процессу.
Уравнения импульсов для абсолютного и относительного движений с учетом потерь можно получить, введя в (9-11) и (9-12) импульс сил трения; в этом случае i, с и w и являются параметрами действительного течения.
При исследовании ступени в рамках упрощенной одномерной схемы потока используется уравнение неразрывности:
m = Fpc = Fpw = Fqp а = F п а а
где Fc — площадь сечения, нормального к вектору скорости с;
Fw — площадь сечения, нормального к вектору относительной скорости w; qc и qw — приведенные расходы при абсолютном и относительном движениях.
Из уравнения неразрывности находим:
где Р Р w y а с* a w — критические плотности и скорости
для абсолютного и относительного потоков.
Очевидно, статические параметры р, .р, Т как в абсолютном, так и в относительном движении одинаковы.
Действительный процесс движения газа в проточной части ступени отличается рядом особенностей, не учитываемых выведенными выше уравнениями. Так, поток газа в зазоре между направляющей и рабочей решетками обладает неравномерностью. В рабочих каналах, воспринимающих поток из зазора, течение газа оказывается периодически нестационарным, с непрерывной пульсацией скоростей и давлений.
Кроме того, поток совершает теплообмен с внешней средой в связи с непроизводительными потерями тепла и вследствие организуемого искусственного охлаждения лопаток, подверженные высоким нагрузкам. В уравнении энергии эта особенность может быть учтена введением соответствующего члена, учитывающего вмешний теплообмен.
При движении в .проточной части основной поток разветвляется; при этом некоторое количество газа, минуя рабочую решетку, протекает в зазоры между статором и ротором. В зависимости от распределения давлений в проточной части может происходить подсос газа через зазоры в основной тоток.
Таким образом, в общем случае поток газа в ступени подвергается различным внешним воздействиям, влияющим на процесс преобразования энергии. Оценка этих воздействий производится на основании данных эксперимента.
9-2. ПАРАМЕТРЫ ПОТОКА В АБСОЛЮТНОМ И ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ. ОДНОМЕРНАЯ СХЕМА
Величину постоянной в правых частях уравнений энергии (9-8) и (9-9)
С 2 . . W 2 — и 2 , . . /г> 1
можно определить из граничных условий.
При расчете ступени турбины обычно известны параметры течения на входе в рабочее колесо. Для входа имеем:
— С и U i + *1 = 2 + *1 = Const.
Обозначив, как и раньше,
где ioc — энтальпия полного изоэнтропического торможения в произвольном сечении потока в абсолютном движении,
запишем (9-13) в такой форме:
или для совершенного газа:
^ де l ocv Тoci — энтальпия и температура изоэнтроЬичбсМб торможения на входе в рабочее колесо в абсолютном движении.
С другой стороны, при полном изоэнтропическом торможении потока в относительном движении его кинетическая энергия обратимо переходит в тепло. Энтальпия торможения определяется очевидным уравнением
Следовательно, уравнение энергии принимает вид:
где i — энтальпия полного торможения относительного
потока на входе в рабочее колесо.
Заметим, что если поток на входе не закручен и си]= = 0, то из (9-15) следует
Такой случай может иметь место только для чисто
реактивной ступени или для ступени центробежного компрессора.
С учетом выражений (9-14) и (9-16) уравнение (9-13) можно записать так:
Соответственно получаем зависимость между температурами торможения в абсолютном и относительном потоках:
_ С п а С„|М, ц2 и?
Уравнение (9-20) показывает, что температура торможения в обшем случае является переменной вдоль струйки величиной не только для абсолютного, но и для относительного движения. Представим (9-20) в несколько иной форме:
Tar + C t, U — C „ U
Разность температур торможения
Из уравнения (9-20a) следует, что температура торможения относительного потока меняется соответственно изменению окружной скорости вдоль трубки тока. При и = const температура Тош постоянна. На этом основании можно заключить, что температура торможения Т постоянна в ступени с осевым потоком газа. В радиальной ступени Tow вдоль трубки тока меняется. Если в такой ступени поток направляется от оси вращения к периферии, то Tow увеличивается. В случае, когда поток движется к оси вращения, Т убывает.
Полученный результат имеет простое физическое объяснение.
Полная энергия относительного потока, пропорциональная Tow, изменяется вследствие работы центробежных сил, в поле которых движется газ. Если радиальные составляющие скорости не равны нулю (сг—шгФ0) и струйка газа движется не только вдоль оси вращения, но и радиально, то центробежные силы совершают работу перемещения частиц в радиальном направлении и увеличивают или уменьшают полную энергию частицы в зависимости от направления потока. Если направление относительного потока совпадает с направлением центробежных сил (радиальная ступень с потоком газа к периферии), то Tow увеличивается. В-противном случае (радиальная ступень с потоком газа к оси вращения) полная энергия уменьшается.
Формула (9-206) показывает, что температура торможения в абсолютном движении во всех случаях убывает. Из рассмотрения принципа работы турбинной ступени следует, что в произвольном сечении трубки тока сиы см!ы1 и возрастает в направлении потока, так как работа к газу подводится.
Вернемся к уравнению энергии (9-13). Заметим, что величина постоянной в правой части уравнения (9-13) различна для разных струек, так как сихих может изменяться при переходе от одной струйки к другой. Отсюда заключаем, что, строго говоря, уравнение энергии следует применять для каждой струйки в отдельности. Для канала в целом уравнение (9-13) может бьпь использовано, если все величины, входящие в это уравнение, подсчитывать как средние по сечению канала.
Уравнению энергии в относительном движении можно придать известную форму, заменяя t по формуле
тогда согласно уравнению (9-16)
2 “TfeZiq — feZTi ’
где pgw, po(B, aow—давление, плотность и скорость звука в изоэнтропически заторможенном относительном потоке.
Подчеркнем еще раз, что скорость звука и статические параметры течения р, р и Г для абсолютного и относительного движений имеют одну и ту же величину.
Скорость звука заторможенного относительного потока меняется вдоль струйки в соответствии с изменением энтальпии iow a OW a *W k—l k P° W _
l ow C p T OW ft—1 2 k—1 k—1 Рою
Аналогичные преобразования для потока в абсолютном движении приводят к соотношению
С помощью этих соотношений нетрудно получить выражение для характерных скоростей а,с, смакс, a.w и т. д. Так, например, для относительного потока находим:
Из уравнения (9-24) следует, что характеристики абсолютного потока, зависящие от величины полной энергии ioc (от параметров торможения), меняются вдоль трубки тока. Следовательно, а,с, смакс и а являются переменными величинами для струйки газа в абсолютном движении.
В относительном движении критическая и максимальная скорости могут меняться или оставаться постоянными в зависимости от того, меняется ли или не меняется вдоль струйки окружная скорость и. Если вдоль струйки и = = const (ступень с осевым потоком), то i = const и соответственно a,w = const и дамакс = const. При переменной вдоль струйки окружной скорости эти основные характеристики потока газа изменяются соответственно изменению и.
Уравнение (9-21) позволяет установить связь между температурами торможения в относительном и абсолютном потоках в следующей форме:
После замены (см., например, треугольники скоростей на рис. 9-2,6)
= 1 ““О — 1 ) = 1 ““О sm 2 (g — а) ‘ ( 9 ‘ 25a )
Уравнение (9-25а) показывает, что вдоль струйки отношение температур торможения меняется. При и = 0 и а=. = 2с„ отношение Т /7’„ = 1. Первый случай-соответ-
для абсолютного потока
Отсюда по известным формулам изоэнтропического процесса:
можно получить связи между -у и Лш, —— и и т. д.
С помощью уравнений (9-27) и (9-28) можно также получить зависимость между параметрами изоэнтропического торможения в абсолютном и относительном потоках:
С помощью уравнения (9-20) легко получить зависимость между параметрами полного торможения на входе и на выходе из колеса.
Для относительного потока получим [см. формулу (9-20а)]
Соответственно для абсолютного потока [см. формулу (9-206)]
с и u i с ы2 u 2
В формулы (9-27) — (9-39) входят безразмерные скорости абсолютного и относительного потоков. Связь между Мс и Мш выражается так:
Последнее уравнение показывает, что отношение температур торможения T0JT0C служит переходным коэффициентом от абсолютного потока к относительному. Эта величина меняется вдоль струйки. На входе и на выходе т
из рабочего колеса для данного режима приобретает
Основные газодинамические зависимости, приведенные выше, справедливы как для аксиальной, так и для радиальной ступеней турбомашины.
Практические расчеты показывают, что влияние центробежного эффекта в осевой ступени невелико 116 . К этому выводу легко также прийти с помощью уравнения (9-33), из которого следует, что если отношение йа/йх мало отличается от единицы, то изменение температуры торможения относительного потока пренебрежимо мало. Только при значительном изменении окружной скорости вдоль трубки тока, как это, например, имеет место в ступени центробежного компрессора или радиальной турбины, влияние указанного эффекта будет существенным.
Для обычных турбинных радиальных ступеней отношение окружных скоростей ujux колеблется в пределах
Рис. 9-7. Изменение температуры торможения относительного потока в зависимости от h2/“i и М w—
1,02—1,10. На основании рис. 9-7 заключаем, что для и2[и 1 = 1,10 относительное изменение температуры торможения Тощ при м,ш1 = 0,3 0,5 составляет 0,25 — 0,70%,
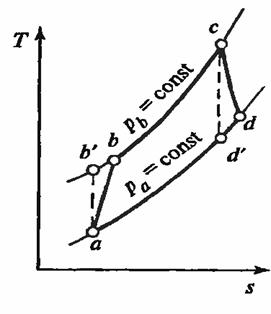
Изобразим изменение состояния газа вдоль струйки в тепловой диаграмме с учетом потерь энергии в элементах ступени турбины. Параметры полного торможения на входе в направляющую решетку находим в точке О (рис. 9-8): Рос и г осг Соответствующие статические параметры определены точкой 0[. Если обозначить статическое давление за направляющей решеткой рх, то точка V фиксирует состояние газа при изоэнтропическом расширении, а точка 1 показывает действительное состояние потока (с учетом потерь). Потеря энергии выражается отрезком 1 — Г.
Давление торможения абсолютного потока за направляющей решеткой будет рш (энтальпия торможения остается
неизменной). Разность р0с — Р0с1 Эквивалентна потерям энергии Дhc.
Коэффициент потерь в направляющей решетке равен:
где Я0 — безразмерная скорость, эквивалентная изоэнтропи-ческому перепаду тепла в ступени Н0.
Разность энтальпий торможения абсолютного и относительного потоков определяется по уравнению (9-19). Откладывая величину i0cl — i0wl от точки О’ на линии f0c] = const, находим точку 2, которая определяет состояние заторможенного относительного потока на входе в рабочее колесо.
В рабочих каналах в результате потерь часть кинетической энергии необратимо переходит в тепло. В результате давление торможения в относительном движении падает. Если вдоль струйки газа окружная скорость не меняется, то соответствующий процесс изображается линией 2—3 (i0 , = const). При увеличении и вдоль струйки (радиальный поток от оси вращения к периферии) iQw возрастает (пунктирная линия 2—3 ! ). Если и уменьшается, то i0w снижается (линия 2— 1 Oail
Поток покидает ступень с некоторой абсолютной скоростью с2. Часть кинетической энергии, эквивалентная скорости с2, является потерей (Дha).
Коэффициент потерь с выходной скоростью
где рт — давление тормол ения абсолютного потока за ступенью;
/?0 — фиктивное давление торможения за ступенью (рис. 9-8).
Как видно из формул, коэффициенты потерь С2 и С3 зависят в неявной форме от — , так как от этой величи-
Рис. 9-8 Процесс в тепловой диаграмме для турбинной ступени 588
и Re на выходе из направляющей решетки.
йы зависят отношения температур -*— и -— . Величи-
также зависит от —; при изменении р- меняются числа М
на Clt характеризующая потери в неподвил ной решетке,
В тепловой диаграмме отложим от точки 4′ вверх величину Дйв; тогда получим точку 4, характеризующую состояние заторможенного абсолютного потока за ступенью-Предположим, что вся кинетическая энергия абсолютного потока за ступенью необратимо переходит в тепло; тогда на изобаре ра в точке 5 определяется состояние газа за ступенью (процесс торможения за ступенью принят изобарическим).
Введем теперь понятие степени реакции. Степенью реакции называют отношение располагаемого теплового перепада на рабочей решетке к полному располагаемому перепаду тепла в ступени. Следовательно, степень реакции указывает ту часть располагаемой потенциальной энергии газа (тепла), которая Преобразуется в механическую работу непосредственно в рабочей решетке (на колесе).
По определению (рис. 9-8)
где /г02 — изоэнтропический располагаемый перепад тепла
в рабочей решетке.
Формулу для степени реакции можно преобразовать к виду:
Отсюда следует, что для аксиальной ступени
степень реакции обращается в нуль при Яв2 = Яда1. Для радиальной ступени р = 0 при
Из этой формулы следует, что степень реакции MoJKet быть равна нулю при движении газа в радиальной ступени от оси вращения к периферии («2 > при Яа] >Ящ2. При движении газа к оси вращения р = 0, если Я^ г 0с2 —
Отсюда с помощью уравнения (9-36) находим:
Тогда к. п. д. ступени на ободе можно найти по фор-
Из формулы видно, что даже в случае, когда потери энергии в направляющей и рабочей решетках отсутствуют (С1 = С2 = 0), к. п. д. ступени на ободе равен нулю при ‘Lcji — 0.
Формула (9-37) показывает, что такое условие выполняется, если
С и1 М 1 = С и2 и г-
Очевидно, что в этом случае поток газа в ступени работы не совершает. Величина Ъсии — 0 и для неподвижного колеса (и1
Легко видеть, что в рассматриваемом случае си2иг = 0, или си2 = 0 (и2 ф 0).
По треугольникам скоростей можно заключить, что при этом выходные потери минимальны, так как при си2 — 0
9-3. УРАВНЕНИЯ ДЛЯ РАСЧЕТА РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОТОКА ПО РАДИУСУ В РАМКАХ СТРУЙНОЙ ТЕОРИИ •
Рассмотрим поток газа через ступень осевой турбомашины (рис. 9-9). Выберем три контрольных сечения: О—0 — перед направляющей решеткой, 1—1 — между направляющей и рабочей решетками и 2—2— за рабочей решеткой.
Рис. 9-9 Схема проточной части ступени с длинными лопатками.
Найдем распределение параметров таэтока по радиусу в двух контрольных сечениях (1—¦
1 и 2—2), если известны: распределение
параметров в сечении О—0, давление газа на корневом или среднем радиусе сечения 2—2, геометрические размеры ступени, число оборотов ротора турбины и аэродинамические характеристики решеток.
Имея в виду трудности, связанные с исследованием пространственного течения сжимаемой жидкости, можно в первом приближении рассмотреть упрощенную осесимметричную схему ,потока в ступени турбомашины.
Так, если принять, что течение в г ступени является установившемся и осесимметричным (д/дд=’0), а радиальные составляющие скорости (cr = w ), а также их произ-‘дс, дс, dw, dw.
дг J весьма малы > то уравнения (1-17а) и (9-1) упрощаются и принимают вид (R=Q=z-
2 ui/r и получить из него первое уравнение (9-43).
Второе уравнение (9-43) выражает условие неизменяемости си по оси ступени. Из третьего уравнения нетрудно получить dca/dz = 0 три dp/dz=0, т. е. если давление по оси не меняется, то осевые составляющие скорости также сохраняются неизменными.
Принятым допущениям в наибольшей степени отвечает поток в контрольных сечениях 1—1 и 2—2 движение в межлопаточных каналах не подчиняется таким упрощенным закономерностям.
Введем дополнительно ряд упрощений. Пренебрегаем периодической нестационарностью потока, вызванной вращением рабочего колеса, или, точнее, считаем, что рассмотрение осредненных по времени скоростей также не вносит существенной ошибки. Предполагаем также, что после перестройки поток в контрольных сечениях движется по цилиндрическим поверхностям (т. е. радиусы кривизны меридионального сечения поверхности тока R на рис. 9-9 достаточно велики). Считаем, что внешний и внутренний теплообмен отсутствует, а решетки ступени обтекаются безотрывно.
Рассмотрим поток за направляющей решеткой. Воспользуемся упрощенным уравнением радиального равновесия (9-43), записав его в следующей форме: для сечения 0—0
где р0, р0, pt, pj, с0, я0, си аг — давления, плотности, скорости и углы потока перед и за направляющей решеткой.
Предполагаем, что функция ai = ai(r) известна. Вид этой функции определяется принятым законом закрутки направляющих лопаток. Очевидно, что поток газа должен удовлетворять уравнениям энергии и неразрывности. Для каждой элементарной кольцевой струйки, протекающей через направляющую решетку, уравнение энергии можно записать в такой форме:
/о’ = ‘t + 4 =^ f ‘ ¦ ( 9 — 45 )
где i’Q — энтальпия торможения в зазоре;
clt, clt iu, ii —скорости и энтальпии газа в конце изоэнтропического и действительного процессов расширения в направляющей решетке;
-ц1 — к. п. д. направляющей решетки (приближенно определяемый как ij^cp 2 ).
Продифференцируем уравнение (9-45) по радиусу г:
Производная характеризует изменение энтальпии
потока в зазоре за направляющей решеткой по радиусу и, как известно, может быть записана таким образом:
Здесь pu — плотность газа в конце изоэнтропического расширения в направляющей решетке; — плотность газа в конце действительного расширения (при наличии потерь).
где ^lt = Cu/u сХ—теоретическая безразмерная скорость за направляющей решеткой.
или с учетом (9-436) di
Подставляя (9-49) в уравнение энергии (9-46), получаем дифференциальное уравнение распределения абсолютных скоростей по радиусу в зазоре:
где hol = (? /2ij1 — располагаемый теплоперепад в направляющей решетке в данном сечении по радиусу.
Интегрируя уравнение (9-50), находим:
где KL — постоянная, отвечающая исходному (среднему или корневому) сечению.
Уравнение (9-51) в рамках рассматриваемой струйной задачи является наиболее общим.
Из (9-48) следует, Ч’го при дозвуковых скоростях и умеренных потерях в направляющей решетке отношение плотностей Рг1?и близко к единице. Расчеты позволяю! — установить ту область значений Яи и %, в которой можно принять = 1. Без большой погрешности такое упрощение допускается прй Яи w 2 h + — = +
где о»! — относительная скорость на входе в рабочую решетку;
— энтальпия газа перед рабочей решеткой;
Tjg — к. п. д. рабочей решетки (т^^ф 2 ); ht — энтальпия газа за рабочей решеткой в изоэн-тропическом процессе.
Теоретическая и действительная скорости за решеткой связаны соотношением
Очевидно, что i2t = i2t (г) и ш2 = ш2 (г) являются искомыми функциями, а тг13 = т)2 (г) и wl = w1 (г) могут рассматриваться как заданные функции радиуса г.
Энтальпия потока за направляющей решеткой определяется по уравнению энергии:
После подстановки i1 в (9-53) находим:
Продифференцировав уравнение энергии, получим (полагаем C ?
I w 2 uw 2 * u ‘l2 I ц I 1 1 __ Г1 /Q СЛД
dr I“ i)j dr ‘ 2tj2 dr «I dr 2 J (9-54)
Заменим в уравнении (9-54)
Уравнения (9-54), (9-55) и (9-56) решаем совместно. После некоторых упрощений получаем искомое дифференциальное уравнение:
Уравнение (9-57) является нелинейным. Оно линеаризуется только в частном случае, когда d(calr)jdr = 0.
Интегрируя (9-57) в этом случае, т. е. с учетом d (c,i г)
где Кг — постоянная, определяемая для исходного (среднего или корневого) сечения.
Условие d(cuir)/dr = 0 выполняется строго при закрутке ступени по методу постоянной циркуляции *. Однако, как показывает опыт, это условие приближенно осуществляется и в ряде других практически важных случаев.
Постоянные К и К2 в уравнениях (9-51) и (9-58) определены, если известны скорости С] и w2 в каком-либо сечении по высоте лопаток. Эта задача решается применением ур-авнения неразрывности для сечений 1-1
1 Поток газа в ступени за направляющей и рабочей решетками является закрученным, т. е. имеет неравномерное поле скоростей как при абсолютном, так и в относительном движении. Как показано в § 5-16, в таком потоке поле полной энергии будет неравномерным.
а 1в> а 1к — углы выхода потока у вершины и соответственно в корне воч сечении, r = rjrk; rk — радиус корневого сечения, г — радиус текущего сечения;
Подставив (9-61) в уравнение (9-50) и проинтегрировав последнее, получим:
Для определения скорости необходимо знать величину в корневом сечении. С этой целью преобразуем уравнение неразрывности (9-59), записав ‘его для сечений 0 — 0 и 1 — 1:
Pi c al r i d r ii
c al = c lA c l sina i = / ‘tft^^ sin a l> C 9 — 65 )
где dj принимается до формуле (9-61,.
Приведенные выше зависимости справедливы, если^поток в зазоре дозвуковой. При смешанных течениях в зазоре, когда в нижней
части ступени (у корневых сечений) Ci>e,i, формула (9-62) неприменима. В этом случае необходимо учитывать отклонение потока в косом срезе направляющей решетки.
Перейдем теперь к расчету потока за ступенью. Воспользуемся основным уравнением (9 57) и проинтегрируем его при т)2= const и d (сп1и) = 0 для принятого закона изменения углов по радиусу
Здесь b»2fe — значение ш2 в корневом сечении;
При известных значениях ш2 легко определяется располагаемый теплоперепад в ступени.
С помощью выведенных уравнений можно рассчитать распределение параметров по радиусу в зазоре н за ступенью с лопатками постоянного профиля.
Располагаемый теплоперепад в направляющей решетке согласно (9 62) будет:
Найдем изменение степени реакции по радиусу:
Л 01 , Л 01к— , , Л 01к Нок
где рк — степень реакции в корневом сечении.
Использовав (9-67), получим:
Отсюда можно получить приближенную формулу для определения реакции на среднем диаметре ступени с незакрученными лопатками, исходя из заданной величины рк в исходном — корневом — сечении. Замечая, что гт = 0/0 — 1 и полагая Ь1 5= 0, из формулы (9-68) получаем:
Формула (9-69) имеет ограниченную область применения Очевидно, что она справедлива для относительно больших 0, так как только в этом случае разность а, у вершины и у корня мала и можно принять b,^0.
Минимальную степень реакции в среднем сечении можно определить, полагая, что в корневом сечении 0. Тогда из (9-69)
или приближенно 5=0)
Изменение работы на венце по радиусу можно найти по формуле:
Функция ся1 (г) также известна. Следовательно, величина Lu (г) определена.
Поле осевых составляющих скоростей за ступенью рассчитывается по формулам:
С а2 = С й2 tg “2 = ^„2 tg h = (°U2 + «) tg h
В заключение отметим, что исходная формула для степени реакции (9-68) позволяет определить разность р у вершины и у корня лопатки. Так как
то после подстановки в (9-68) получим:
где рв — степень реакции у вершины.
Для прикидочных расчётов^можйо^рёйомендойать формулу 1 — рв (в—1 2
Используя полученные соотношения, можно проанализировать изменения параметров ,по радиусу в зазоре и за ступенью и оценить дополнительные потери, возникающие в ступени с лопатками постоянного профиля.
Рис 9-10. Сравнение опытных и расчетных значенлй степени реакции в различных сечениях по радиусу ступени с лопатками постоянного профиля; в = 7,73; М0 = 0,65.
Результаты соответствующих расчетов показывают, что дополнительные потери в ступени с незакрученными лопатками обусловливаются увеличением выходных потерь, изменением угла входа потока на рабочую ’решетку, а также изменением отдаваемой работы по радиусу. За ступенью поток вихревой; выравнивание поля скоростей сопровождается потерями кинетической энергии, которые должны быть включены в общий баланс потерь ступени.
Результаты расчетов по предлагаемой методике удовлетворительно совпадают с экспериментальными данными.
Подробное экспериментальное исследование потока в зазоре и за ступенью с цилиндрическими лопатками было выполнено в МЭИ при Q = d/l = 7,73. Был произведен расчет испытанных ступеней по приближенному методу, изложенному выше. Соответствующие кривые изменения реакции по радиусу приведены на рис. 9-10. Сравнение показывает удовлетворительную сходимость опытных и расчетных значений реакции. Опытные и расчетные значения углов, давлений и скоростей также удовлетворительно совпадают.
В заключение отметим, что при больших в изменение углов ai и Рг по радиусу невелико.
Расчет скоростей Ci и w2 в таких ступенях можно производить по формулам, которые легко получить из основных уравнений (9-50) и (9-57) при следующих допущениях: г) 1 = const; т)2” const; ai = const и Рг = const.
9-5. НЕКОТОРЫЕ СПОСОБЫ ПРОФИЛИРОВАНИЯ ДЛИННЫХ ЛОПАТОК СТУПЕНЕЙ С ОСЕВЫМ ПОТОКОМ ГАЗА
Изложенная выше методика расчета ступеней с лопатками постоянного профиля позволяет оценить дополнительные потери в ступени, обусловленные изменением параметров и углов потока по радиусу в зазоре, а также возрастанием выходных потерь.
Результаты такого расчета приведены на рис. 9-11. Здесь даны кривые, устанавливающие дополнительные потери в ступени с лопатками постоянного профиля в зависимости от Q=d/l. Кроме того, на график нанесены опытные значения дополнительных потерь Ат]м. При е 2 ^-^ = 0. (9-50а)
и согласно принятому допущению саХ = const, то уравнение (9-50а) преобразуется к виду:
Интегрируя это уравнение, получаем: calr = const.
Последнее условие выражает постоянство циркуляции скорости вокруг направляющей решетки. Действительно, в простейшем случае осевого входа в направляющую решетку (с 0 = 0) циркуляция скорости равна:
с »о) = tc ,n —^Г с и — const —
где z — число лопаток в решетке.
Основоположником рассматриваемого метода является Н. Е Жуковский. Еще в 1912 г. при исследовании воздушных винтов Н. Е. Жуковский показал, что осевые скорости постоянны в радиальном направлении, если изменение окружных составляющих скоростей соответствует закону постоянства циркуляции. Хорошо известно, что воздушные бинты, а затем и вентиляторы, построенные согласно вихревой теории Н. Е. Жуковского, отличались высокой экономичностью. Для расчета длинных лопаток паровых и газовых тур’бин этот метод был впервые применен В. В. Уваровым.
С помощью уравнения (9-50а) нетрудно пайти распределение абсолютных скоростей в зазоре:
Изменение реакции по радиусу устанавливается с помощью очевидных соотношений
В соответствии с условием cat г = const можно найти изменение углов абсолютной скорости по радиусу в таком виде:
Закрутку лопаток по условию постоянства циркуляции скорости можно осуществить с учетом потерь в решетках.
Для адиабатического течения (с учетом потерь) расчетные зависимости, полученные путем интегрирования исходных дифференциальных уравнений, даны в табл. 9-1.
Для течения с потерями, как это видно из формул, приведенных в табл. 9-1, условия cur = const и cai=eonst являются несовместимыми. При условии равномерного поля осевых скоростей в зазоре циркуляции скорости вокруг направляющей лопатки должны увеличиваться к ее вершине. Если в основу профилирования ступени положено условие постоянства циркуляции скорости, то осевые скорости в зазоре также несколько .увеличиваются к вершине.
Адиабатическое течение в зазоре при aj = const и rji = const подчиняется уравнению, получаемому инте-грированием (9-50), в следующем виде:
c al =c al/ c ulK cos 01,
1 — Tj! cos 2 X J[__
j/” 1 — r^cos^iK (1 — r 3 )
r 1 — cos 2 aj K lr]2 + (1 —TjO r 2 ]
Следовательно, располагаемый теплоперепад в направляющей решетке будет:
— “о— 2l li cos2 a i
Отношение скоростей меняется по радиусу в соответствии с формулой
где x = u.Jc|K — отношение скоростей для корневого сечения.
Угол относительного потока
Следует подчеркнуть, что осуществление метода закрутки при ai = const приводит к направляющим лопаткам переменного профиля по высоте, так как при малых 0 значительно меняются шаг лопаток и скорость с j вдоль радиуса. Следовательно, чтоб ы> осу щес т в ит ь условие ai=const, необходимо менять установочный угол профиля ау, т. е. выполнять лопатку закрученной. При больших скоростях необходимо также учитывать влияние сжимаемости на средний угол за решеткой, что также приводит к необходимости закручивать направляющие лопатки.
Для большого числа ступеней представляется возможным направляющие лопатки выполнять без закрутки. Расчет направляющих решегок производится по формулам, приведенным в § 9-4. С помощью этих соотношений рассчитываются параметры потока в зазоре.
Расчет рабочих лопаток как при ai = const, так и при «1 —f( r ) производится, исходя из принятых условий за ступенью. Как указывалось, могут быть приняты условия отсутствия закрутки потока на выходе (си2 = 0), постоянства работы по радиусу (Lu = const) и др.
Расчет ступени при течении, близком к цилиндрическому, можно осуществить, разбив поток на ряд элементарных кольцевых струек. В пределах каждой струйки можно считать задачу одномерной и применять обычную методику расчета. Закрутка направляющей решетки, вообще говоря, может быть выбрана любой: ai = const; сиГ=const; a=f(r). При этом, естественно, для определения параметров в зазоре можно воспользоваться одним из частных решений (9-50). Определив параметры в зазоре, записываем уравнения неразрывности для каждой струйки в контрольных сечениях 1—1 и 2—2:
где AG — расход пара через элементарную струйку;
и Ргt — плотности в конце изоэнтропического расширения в направляющей и рабочей решетках;
cu, w2t — теоретические скорости выхода потока; ft и /2 — площади выходных сечений в пределах одной элементарной струйки; jj-i, ja2 — коэффициенты расхода в данном кольцевом сечении направляющей и рабочей решеток.
Из уравнения неразрывности и треугольников скоростей определяем параметры, необходимые для проектирования рабочей решетки. Полный расход газа через ступень О равен сумме расходов по всем элементарным струйкам. Общий к. п. д. ступени находится по к. п. д. элементарных струек как усредненный по расходу.
При подобном методе расчета коэффициенты расхода щ и fig и коэффициенты скорости следует принимать переменными, зависящими от геометрических и режимных параметров в рассматриваемых сечениях решеток. Описанный метод расчета весьма прост и дает надежные результаты.
Построение направляющей и рабочей лопаток осуществляется по данным расчета закрутки. По вычисленным значениям Ме1 (г) и а, (г) подбираются профили в корневых, средних и верхних сечениях направляющей решетки. При больших теплоперепадах в ступени в корневых сечениях >1, а в периферийных М^, f /
о.г о.« o,s о,8 р Рис. 9-12. Сопоставление некоторых методов закрутки лопаток.
сти углов входа потока Pi в верхнем и корневом сечениях, к снижению лотерь от утечек, уменьшению осе-зых усилий и т. п. Для компрессорной ступени с реакцией р=0,5 за счет выравнивания поля скоростей по высоте может быть отодвинута предельная граница по числу М, повышены окружные скорости и, следовательно, увеличен коэффициент напора при сохранении высокой экономичности ступени.
Рис. 9-13 Схема кольцевой решетки направляющих профилей с наклонными кромками и меридиональным профилированием.
Для ступеней турбин с небольшими высотами лопаток (Т С 1
Как указывалось (§ 8-8), применение меридионального профилирования в ступенях с небольшими высо-
Рис. 9-14. Зависимость к. п. д. к)ог и реакции от и/с0 для ступени с меридиональным профилированием (КД-2-2Ам) и ступени с цилиндрическими обводами (КД-2-2А); 8 = 16; = 0,5.
тами лопаток позволяет не только уменьшить разность [реакций, ,но и значительно уменьшить потери ® ‘Направляющих решетках. На рис. 9-14 представлены резуль-гаты испытаний двух ступеней (ii»0,5; 0=16) с криволинейным и цилиндрическим обводами верхнего бандажа. Видно, что ступень с мериодинальным профилированием имеет более высокий к. П. д. (на 1,5—2%), а разность реакций Др — рв — рк уменьшается более чем в 3 раза (с 16 до 5%).
Для ступеней с 0 г L F
(где Fr—радиальная составляющая силы воздействия лопаток на поток) видно, что при 7v у>+20°. Графики изменения потерь по высоте решеток (рис. 9-16) показывают, что для отрицательных углов наклона потери возрастают в корневых сечениях, где возникает отрыв потока. Для решеток с наклоном лопаток по потоку, когда осуществляется поджатие потока в корневых сечениях, .потери увеличиваются в периферийных сечениях.
Опыты показали, что одновременным введением меридионального профилирования верхнего обвода решетки и наклоном лопаток можно уменьшить потери в верхних сечениях (у>0). При этом оба фактора — наклон лопаток по потоку и профилирование верхнего
1 Исследование ступеней с наклонными лопатками проведены Ю. И. Митюшкиным (ЛМЗ) и Г. А. Филипповым (МЭИ).
обвода — позволяют более резко снйзить разность реакций Др — рв рк.
Приближенная формула для определения реакции в ступени с различными углами наклона лопаток у может быть получена путем совместного решения уравне-
Рис. 9-16. Характер изменения потерь по высоте решетки при различных углах наклона лопаток (в = 8,5; /, = 1,0; а, = 15°).
ний количества движения и радиального равновесия цилиндрического потока (9-73). Сила воздействия лопаток на поток определяется через окружную составляющую по уравнению (сг«0):
где Рп — окружная составляющая силы воздействия лопаток на поток.
ГТринйв линейный з&кон изменения tu ho Ширийё решетки для средней линии канала са = хся1/В, получим:
Подставляя Fr в уравнение (9-73), находим:
dp Cj cos c?j C| sin a, cos a,
Из последнего уравнения совместно с уравнением энергии получим:
/Is-т dr — cos 2 a. — .
Проинтегрировав это уравнение для случая at = const получим распределение скоростей по высоте лопаток:
i Г sin dj cos a, (r,— rR) eX ^ I о tg (90 — y)
Реакция в произвольном сечении зазора рассчитывается по формуле
2sin a, cos (r, — r )
Разность реакций при pA = 0 и 6^1,5В (b — хорда профиля)
Полученные формулы дают несколько завышенные значения разности реакций, что связано в основном с отклонением потока в зазоре ступени от коаксиального, наличием радиальных перетеканий газа в пограничном слое лопаток, утечками в ступени, влиянием рабочего колеса. Погрешность расчета объясняется также принятым приближенным законом изменения си по оси канала и пр.
Влияние перечисленных факторов учитывается по -опытным данным введением коэффициента Л = 0,65 в формулу (9-76).
Расчет реакции в ступени с наклоном лопаток по потоку и меридиональным профилированием зерхнего обвода осуществляется по формуле
полученной с учетом влияния кривизны верхнего обвода на распределение скоростей по радиусу в зазоре.
Опыт подтверждает’ удовлетворительную точность формулы (9-77) при 0 > 6.
Для ступеней с малыми в е /„, угол входа потока уменьшился со 155° до 127°. Число Мс1 возросло у вершины лопатки до 0,9, а число М^г уменьшилось до Мда2=1>08.
Последние ступени турбин часто приходится выполнять с коническими обводами (рис. 9-12). Наличие конусности приводит к уменьшению реакции в ступени.
Рис. 9-17. Изменение параметров по высоте лопатки (0 = 2,6; е2 = 0,27).
——с наклоном кромок, -—кромки радиальные.
Для конусной направляющей решетки изменение реакции по радиусу можно приближенно определить по формуле
где /C,=l-<-siii 2 a,tg 2 8B — коэффициент, учитывающий влияние конусности; 8в — угол конусности у вершины.
ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ГАЗОВЫХ ПОТОКОВ И ПРОТОЧНОЙ ЧАСТИ ТУРБОМАШИН
10-1. ЭКСПЕРИМЕНТАЛЬНЫЕ СТЕНДЫ ДЛЯ ИССЛЕДОВАНИЯ ПРОТОЧНЫХ ЧАСТЕЙ ТУРБОМАЩИН
Задачи опытного исследования проточной части турбомашин можно разбить на тр’и группы В первую грулпу включаются вопросы, связанные с исследованием структуры потока в отдельных, рассматриваемых изолированно элементах ступени и в первую очередь в направляющей и рабочей решетках
Вторая группа задач заключается в дифференцированном изучении физических явлений, происходящих в ступени
Третья группа задач сводится к определению опытных коэффициентов, необходимых для теплового расчета турбомашины, и к выяснению зависимости этих коэффициентов от основных конструктивных, геометрических и режимных параметров ступени
Основные требования к эксперименту в лабораторных условиях формулируются теорией подобия Практически не все эти требования могут быть реализованы с одинаковой степенью точности, так как действительные процессы в турбомашине отличаются большой сложностью Поэтому при постановке эксперимента в каждом отдельном случае следует установить наиболге существенные особенности процесса, пренебрегая его второстепенными признаками Правильное решение этого вопроса определяет направление и методику экопримента, а также теоретическую и практическую ценность результатов исследования Если основной целью эиспер лмента является получение интегральных характеристик ступени, то очевидно, что в модельных условиях должны быть воспроизведены все наиболее существенные признаки процесса Поэтому опытное исследование характеристик ступени необходимо проводить на специальных экспериментальной турбине или экспериментальном компрессоре, позволяющих установить надежные значения характеристик и изучить основные особенности потока в решетках
Последняя задача, однако, решается в экспериментальной ча^-шине нелегко, так как требует применения сложной специальней измерительной аппаратуры. Поэтому при детальном изучении обтекания решеток, при изучении механизма образовании и развития потерь в изолированно рассматриваемых решетках необходимо прибегать и к другим, более простым методам эксперимента, поступаясь некоторыми требованиями теории подобия Отсюда следует, что наряду с использованием экспериментальной турбомашичы в качестве основного метода исследования необходимо применять и более простые и поэтому широко распространенные методы испытания неподвижных решеток
Исследования элементов проточной части паровых и газовых турбин могут производиться на водяном паре или на воздухе, при-
Чем схема йсйктателыШй Менда сущ&стйемно За1й?йт От Приме няемого рабочего тела Исследования элементов ком пресс о,р а производятся, естественно, на воздухе
Рис 10-1 Принципиальная схема воздушного экспериментального стенда 1 — двигатель; 2—компрессор, 3— ресивер, 4—фильтр; 5 — подогреватель; 6 и 7 —статические установки, 8, ^—экспериментальная турбина 10 — установка для взвешивания реактивных усилий, 11 — аэродинамическая труба, 12 — оптическая установка, 13—холодильник, / 100° С значительно проще, че>м «а паре при температурах 250—350° С Это определило широкое применение воздуха в лабораторных исследованиях проточных частей цурбомашин
Однако ряд задач, связанных с длительной работой эксперимента тыкых установок с большими секундными расходами и при больших скоростях, требует чрезвычайно мощных и громоздких компрессорных установок Работы, связанные с исследованием последних ступеней конденсационных паровых турбин, могут проводиться на воздухе только частично, а ряд вопросов вообще не может быть решен на воздушном стенде
Оптимальным решением, дающим наибольшею возможность ведения различных исследований проточных частей турбин с минимальной затратой времени и средств, является использование ком бинированного паровоздушного стенда, принципиальная схема которого приведена на рис 10-2
Большинство установок такого стенда может работать как на паре, так и на воздухе, что позвочяет выбирать оптимальный для данного эксперимента вид рабочего тела Воздушный контур стемда-не отличается от приведенного на рис 10-1 Использование пара позволяет легко получать большие секундные расходы, большие скорости, независимо менять числа М и Re, обеапечивает проведение всех исследований, связанных с влажностью Пар через редукционно-охладительную установку 29 подается к экспериментальным установкам стенда, проходит через них и направляется в основной конденсатор 21 Конденсат конденсатным насосом 24 подается в мерный бак 25, а затем в линию возврата конденсата ТЭЦ
Паровоздушный стенд состоит из установки для исследования кольцевых неподвижных решеток 7, высокооборотной одноступенчатой экспериментальной осевой турбины 8, двухвальной экспериментальной турбины 14, предназначенной в основном для исследования последних ступеней, экспериментальной турбины для исследования радиально осевых ступеней 20, осевого 26 и центробежного 27 экспериментальных компрессоров с паротурбинным приводом 28 и установки для испытания плоских решеток 6
При необходимости в паровоздушном стенде могут быть использованы эжекторные аэродинамические трубы 18 и 19, воздушный поток в которых создается паровым эжектором, засасывающим воздух из атмосферы
В схему стенда включен блок 17, позволяющий устанавливать для периодических испытаний различные вспомогательные детали турбин
Для отсоса пара из уплотнений экспериментальных турбин используется вспомогательный конденсатор 23 Вакуум в конденсаторах поддерживается паровыми эжекторами 22
Выхлопные патрубки турбин жепательчо снабжать дроссельными устройствами, позволяющими поднимать противодавление за рабочим колесом до 3—5 ата Для подавляющего большинства экспериментов достаточно давление свежего пара 5—7 ата при температуре 250—350° С
Редукционно-охладительная установка должна допускать питание стендов не только перегретым паром пониженных параметров, но и влажным паром
💡 Видео
Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

Алгоритм решения задач на Закон сохранения энергииСкачать

Закон сохранения энергии. 9 класс. Решение задачСкачать

Физика 10 класс (Урок№13 - Работа. Мощность. Энергия. Закон сохранения механической энергии.)Скачать

Закон сохранения и превращения энергии. 9 класс.Скачать

Урок 123. Закон сохранения и превращения энергии. КПД. МощностьСкачать

Галилео. Эксперимент. Закон сохранения энергииСкачать

Применение закона сохранения и превращения механической энергии. Практическая часть. 9 класс.Скачать

Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать

Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

Урок 126. Задачи на закон сохранения энергии (ч.1)Скачать

Физика - импульс и закон сохранения импульсаСкачать

Потенциальная и кинетическая энергияСкачать

ФИЗИКА 10 класс: Закон сохранения энергииСкачать

ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ за 12 МИНУТ в ЕГЭ по Физике | Николай НьютонСкачать

Как нарушить закон сохранения энергии?Скачать

8 класс, 7 урок, Закон сохранения энергии в тепловых процессахСкачать