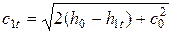Расширение рабочего тела в каналах соплового аппарата
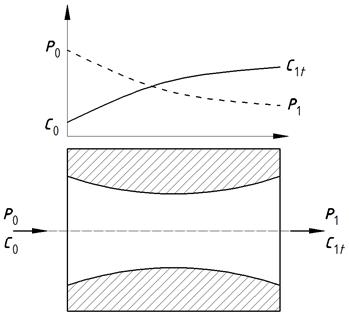
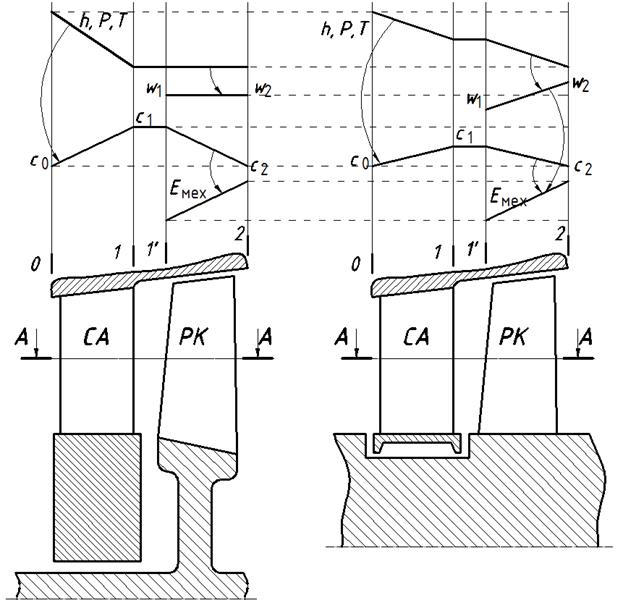
Рассмотрим применение основных уравнений движения сжимаемой жидкости на примере истечения газа из сопел (рис. 5.1).
Это впоследствии поможет нам лучше понять механизм работы ступени, кроме того введем несколько чрезвычайно важных понятий, которые используются в теории ступени турбомашин.
Рис. 5.1. Истечение газа из сопла
Запишем уравнение сохранения энергии для истечения идеального газа из сопла:
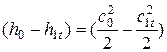
т.е. изменение кинетической энергии определяется изменением энергии потенциальной при отсутствии теплообмена с окружающей средой.
Учитывая уравнение состояния идеального газа
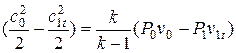
где 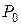
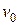
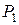
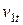
При такой записи уравнения сохранения энергии не нужно знать закон изменения состояния потока, а только начальное и конечное состояние рабочего тела.
Зная 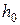
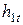
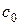
При отсутствии потерь процесс расширения в сопле пойдет по изоэнтропе (s=const). Зная давление в конце процесса расширения 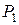
Если скоростью 
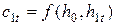
Если же скоростью 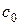
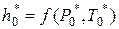
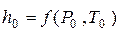
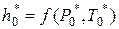
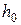
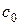
Поэтому параметры 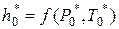
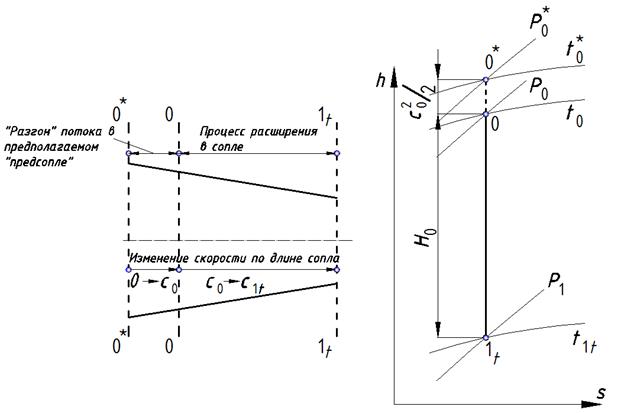
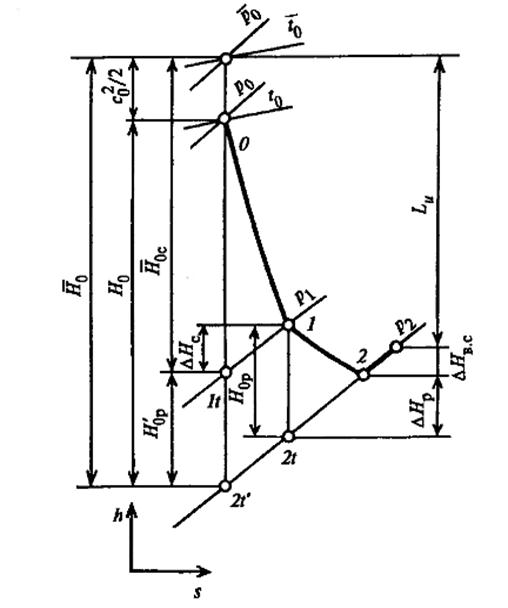
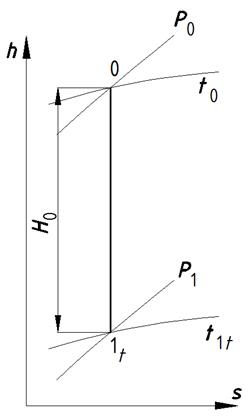
При построении процесса в h –s – диаграмме необходимо отложить от точки 0 вверх по изоэнтропе отрезок равный 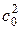

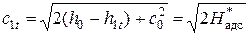
где 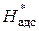
Теплоперепадом называют разницу энтальпий на входе и выходе из некого устройства (сопло, рабочее колесо, ступень, турбина и т.д.), которая показывает снижение внутренней энергии и фактически, как мы уже знает, равна работе, совершаемой данным устройством.
Рис. 5.3. К пояснению понятия «заторможенные параметры потока»
Если скорость потока 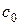
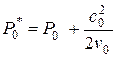
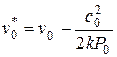
где 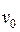
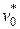
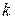
До сих пор мы говорили о расширении в сопле идеального газа, в котором отсутствует взаимодействие между молекулами (отсутствует вязкость. При взаимодействии такого газа с поверхностями, образующими канал сопла не возникает пограничного слоя, т.е. отсутствуют потери на трение.
Этого нельзя сказать о реальном газе. Пограничный слой, который образуется при обтекании реальным газом следствие возникающих потерь приводит к снижению проходного сечения сопла и, как следствие, снижению расхода рабочего тела через сопло. Отношение действительного расхода рабочего тела 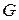
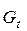
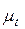
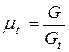
Коэффициент расхода достаточно высок для сопел и составляет 0,95…0,97.
При истечении идеального рабочего тела из сопла вся внутренняя энергия рабочего тела преобразуется в кинетическую. В действительности часть энергии рассеивается и в виде тепла сообщается рабочему телу. Вследствие этого энтальпия рабочего тела на выходе из сопла несколько возрастает до значения 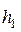
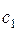
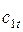
Для сравнения реального процесса с теоретическим используют понятие коэффициент скорости 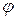
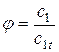
Коэффициент скорости для сопел также достаточно высок и достигает значений 0,95…0,98.
Теперь мы можем достроить диаграмму расширения газа в сопле.
Расширение в реальном процессе также пойдет до давления 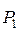
Тогда для реального рабочего тела уравнение сохранения энергии можно записать между точками 0 и 1:
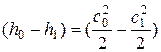
Также можно записать:
Dhc= 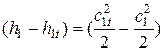
Величина Dhc – будет обозначать потери в соплах.
Используя понятие коэффициента скорости, выражение для величины потерь в соплах возможно преобразовать:
Dhc= 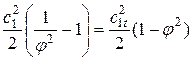
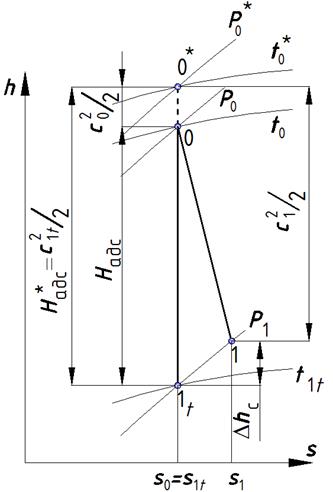
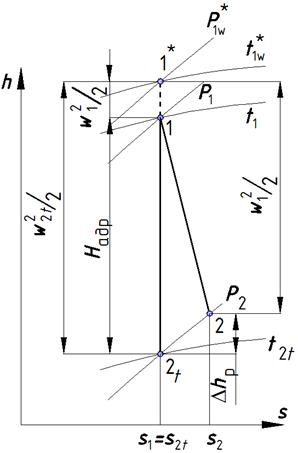
Рис. 5.4. Процесс истечения рабочего тела из сопла в h-s – диаграмме
Однако чаще удобнее пользоваться не абсолютными значения потерь, а относительными. Для этого потери в соплах необходимо разделить на теплоперепад сопла:
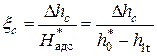
Коэффициент потерь в соплах связан с коэффициентом скорости сопла. Пропуская некоторые несложные преобразования, можно записать:
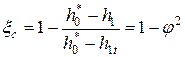
В заключении необходимо отметить, что коэффициент потерь 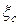
Расширение рабочего тела в каналах рабочей решетки
Все выкладки, приведенные в предыдущем разделе для соплового аппарата, имеют силу и для расширения рабочего тела в рабочей решетке.
Однако существуют и свои особенности.
Диаграмма расширения для каналов рабочей решетки строится не по абсолютным скоростям потока, а по относительным.
Расширение рабочего тела в РК начинается в точке 1 (см. рис. 5.5). При отсутствии потерь (рабочее тело – идеальный газ) процесс пойдет по изоэнтропе в точку 2t до давления 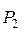
Рис. 5.5. Процесс расширения рабочего тела в рабочих решетках
в h-s – диаграмме
Для теоретического процесса расширения будет справедлива следующая запись уравнения сохранения энергии:
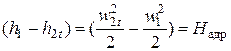
где 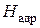
При расширении реального газа часть энергии также будет рассеиваться в тепло, что приведет к росту энтальпии рабочего тела в конце процесса расширения, а реальная скорость 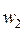
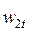
Несовершенство течения в рабочем колесе принято характеризовать коэффициентом скорости 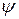
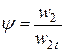
Коэффициент скорости для рабочего колеса несколько ниже, чем в соплах, вследствие турбулизации потока за сопловым аппаратом, а также за счет вращения рабочего колеса и достигает значений 0,93…0,96.
Расширение в реальном процессе пойдет до давления 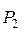
Для реального процесса можно записать:
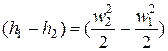
Потери в рабочем колесе будут равны:
Dhр= 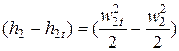
Используя понятие коэффициента скорости, выражение для величины потерь в рабочем колесе возможно преобразовать:
Dhр= 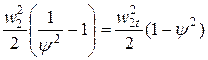
Как и для сопел введем понятие относительных потерь:
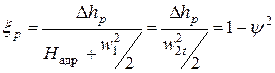
Коэффициенты скорости 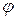
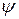
Потери с выходной скоростью
Мы уже знаем, что вследствие вязкости рабочего тела при обтекании потоком сопловых и рабочих лопаток возникают потери на трение, которые приводят к некоторой недовыработке ступенью располагаемой работы.
Однако в ступени существует еще одна потеря, связанная с тем, что поток, уходя со ступени, имеет некоторую скорость 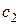
Вместе с этой скоростью из ступени уходит часть энергии равная 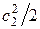
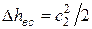
Наличие потери с выходной скоростью приводит к уменьшению полезной работы ступени, что, естественно, снижает КПД ступени.
В многоступенчатых турбинах энергия 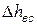
Для потерь в соплах и рабочих решетках, которые были рассмотрены ранее характерно увеличение энтропий, что связано с переходом части энергии в тепло. Для потери с выходной скоростью 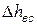
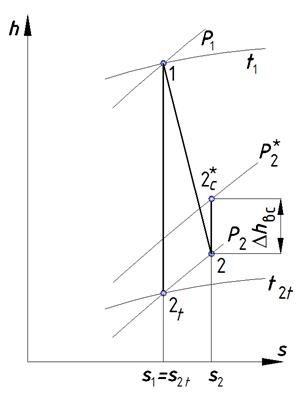
Рис. 5.6. Изображение потерь с выходной скоростью на h-s – диаграмме
Изображение процесса расширения рабочего тела в ступени в h-s – диаграмме
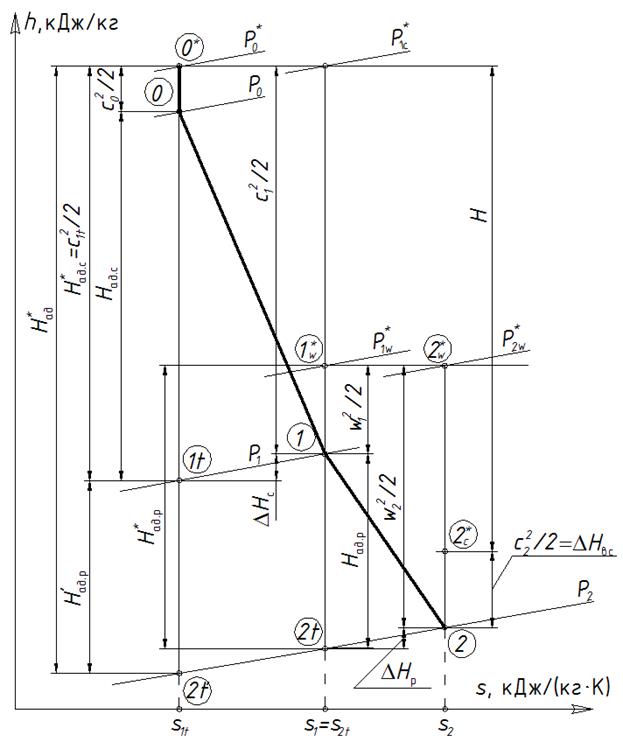
Рассмотрев по отдельность процессы расширения в элементах турбинной ступени и потери, которые при этом возникают, мы можем легко изобразить процесс расширения рабочего тела в ступени в h-s – диаграмме. Для этого надо совместить рис. 5.4-5.6. на одной диаграмме (см. рис. 5.7).
Рис. 5.6. Ход процесса расширения рабочего тела в ступени на i-S диаграмме
На общей диаграмме расширения рабочего тела в ступени есть ряд особенностей, которые было невозможно изобразить при раздельном рассмотрении процесса расширения.
1. Кривая процесса расширения рабочего тела в реальном процессе в рабочей решетке (линия 1-2) более пологая, чем для соплового аппарата (линия 0-1), что связано с более высоким уровнем потерь в рабочей решетке.
2. В силу того, что изобары на h-s – диаграмме расходятся незначительно, можно говорить о том, что отрезки между точками 1-2t и 1-2t’ равны между собой. Если расстояние между точками 1-2t – эторасполагаемый теплоперепад на рабочее колесо 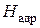
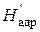
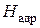
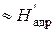
3. После сделанных преобразований на h-s – диаграмме хорошо видно, что
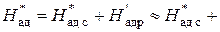
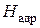
т.е. располагаемый теплоперепад ступени, отсчитанный от полных параметров, будет равен сумме располагаемых теплоперпадов на сопловой аппарат и рабочее колесо.
4. Расстояние между точками 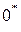
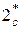
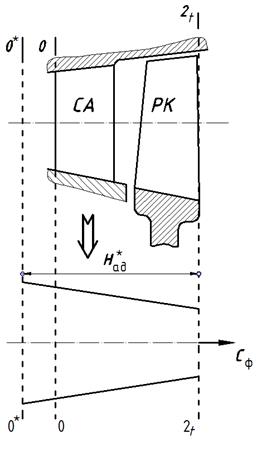
Для дальнейшего изложения теории ступени турбомашины необходимо ввести еще одно важнейшее понятие.
Представим, что рассматриваемую ступень, состоящую из соплового аппарата и рабочего колеса, мы меняем на эквивалентное сопло. При этом теплоперепад на эквивалентное сопло равен теплоперепаду на ступень, отсчитанному от параметров торможении 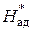
Тогда при срабатывании теплоперепада 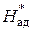
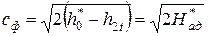
где 
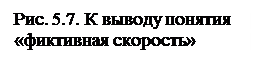
Понятие степени реактивности
Мы уже знаем, что в турбинной ступени происходит преобразование потенциальной энергии пара сначала в кинетическую энергию струй потока, а затем в механическую энергию вращения ротора. При этом общий теплоперепад ступени делится между сопловым аппаратом и рабочим колесом:
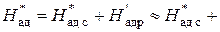
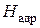
Пропорции, в которых происходит это разделение можно увидеть при рассмотрении h-s – диаграммы расширения рабочего тела в ступени.
Для качественного описания этих соотношений вводится понятие степени реактивности ступени.
Степенью реактивности ступени называют отношение располагаемого теплоперепада на рабочую решетку к суммарному адиабатическому теплоперепаду всей ступени, подсчитанному от параметров торможения:
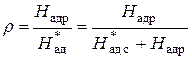
Степень реактивности показывает какая доля располагаемого теплоперепада ступени срабатывается в ее рабочих каналах.
Название связано с тем, что при расширении рабочего тела в рабочих каналах поток ускоряется и возникает дополнительная реактивная сила, которая передает дополнительный импульс вращению ротора.
Понятие степени реактивности согласно тому определению, которое было дано выше, является термодинамической характеристикой ступени, поэтому оценивать ступень по данному понятию удобнее всего по h-s – диаграмме расширения рабочего тела в ступени (рис. 5.8 б).
По значению степени реактивности выделяют 2 типа ступеней:
— активные – со степень реактивности 0…0,25;
— реактивные – со степенью реактивности 0,25…0,50.
При этом в чисто активной ступени степень реактивности r=0 – все расширение рабочего тела происходит в сопловом аппарате, а в рабочем колесе осуществляется только разворот потока (h-s – диаграмма показана на рис. 5.8 а).
В чисто реактивной ступени (r=0.5) теплоперепад поровну делиться между сопловым аппаратом и рабочим колесом, т.е. 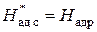
Деление ступеней на активные и реактивные довольно условно и справедливо в полной мере лишь для ступеней с малой верностью ( 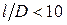
0,05 в корне и до 0,6…0,7 на периферии), что не позволяет использовать характеристики «активная» или «реактивная».
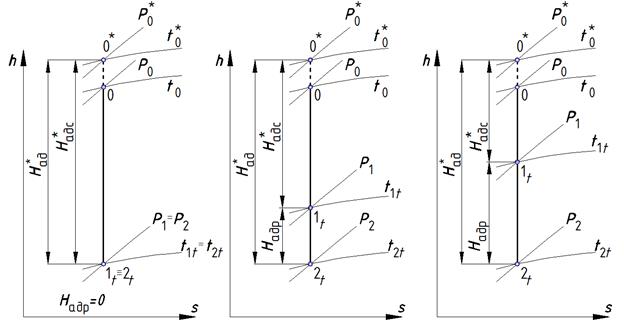
Рис. 5.8. Диаграммы расширения для ступеней различного типа: а. – чисто активная ступень; б. – общий случай; в. – ступень чисто реактивного типа
Помимо термодинамической степени реактивности существует понятии кинематической степени реактивности, которая подсчитывается по кинематическим параметрам (компонентам треугольников скоростей ступени):
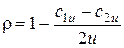
Активный и реактивный принцип преобразования энергии в турбинной ступени
После того, как мы дали определение степени реактивности и более четко разделили ступени на активные и реактивные, необходимо чуть подробнее остановиться на некоторых отличиях в активном и реактивном принципах преобразования энергии в ступенях.
Рассмотрим 2 крайних случая: чисто активную и чисто реактивную ступени – и изобразим схемы ступеней данных типов и графики изменения параметров по длине их проточной части (см. рис. 5.9).
Какие-либо комментарии к рис. 5.9 являются, в данном случае, излишними. Студентам предлагается провести самостоятельный анализ данного рисунка на основании тех знаний, которые они приобрели в ходе предыдущих лекций.
Рис. 5.9. Активный (а) и реактивный (б) принципы преобразования энергии в турбинных ступенях
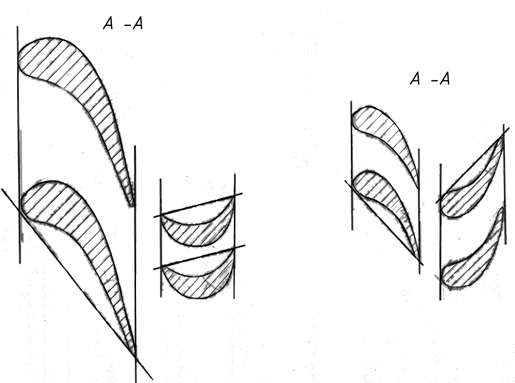
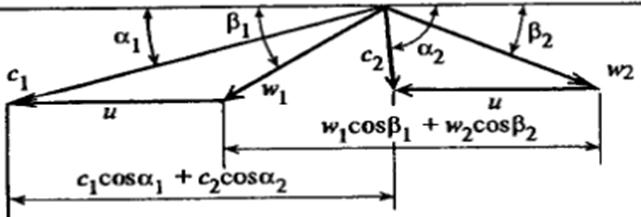
На рис. 5.10 показаны лопаточные профили и треугольники скоростей. Отметим некоторые их особенности:
— В рабочей решетке ступени активного типа не происходит расширения рабочего тела, поэтому межлопаточный канал имеет постоянное проходное сечение. Это определяет следующие соотношения в треугольниках скоростей: 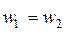
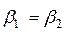
— С ступени реактивного типа расширение рабочего тела происходит в равной степени в сопловом аппарате и рабочем колесе, поэтому профили СЛ и РЛ конгруэнтны, т.е. имеют одинаковую форму, но развернуты под разными углами. Треугольники скоростей в свою очередь, симметричны, а соотношения кинематических параметров следующие: 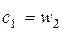
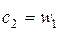
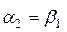
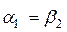
Рис. 5.10. Профили лопаточного аппарата и треугольники скоростей активной (а) и реактивной (б) турбинных ступеней
Диаграммы расширения рабочего тела для обоих типов ступеней были показаны на рис. 5.8.
Таким образом, тип ступени предопределяет конструкцию ступени и турбины, кинематические и термодинамические соотношения в ступени, форму профиле и др.
Особенности проектирования ступеней и глубокие конструктивные различия меду ступенями двух типов таковы, что завод, специализирующийся на турбинах активного (реактивного) типов исключительно редко способен выпускать турбины второго типа.
Видео:Закон БернуллиСкачать

Течение рабочего тела в соплах.
Процесс расширения рабочего тела в диаграмме “ S — I ”
Турбинная ступень состоит из двух лопаточных решеток — сопловой и рабочей, в межлопаточных каналах которых происходит расширение газа. В общем случае газ расширяется последовательно в обеих решетках (реактивный процесс), в частном случае — только в сопловой (активный процесс).
Рассмотренная в предыдущих разделах теория истечения газа из сопел применима к неподвижным (сопловым) и подвижным (рабочим) турбинным решеткам.
Сопловые решетки могут образовывать суживающиеся каналы (для дозвуковых или околозвуковых скоростей) или расширяющиеся сопла Лаваля (для сверхзвуковых скоростей). В обоих случаях проходным сечением, определяющим расход газа, надо считать сечение, имеющее минимальную площадь.
Рабочие решетки, как правило, выполняют конфузорными или с постоянным поперечным сечением по длине канала. Газ входит в эти решетки с относительной скоростью W1, а выходит со скоростью W 2.
На рис.2.2. схематически изображен в координатах S-I процесс расширения газа в реактивной ступени. В турбинной ступени газ расширяется от давления P о* до P 2 по условной политропеAoA2. Располагаемая работа изоэнтропийного расширения газа в ступени определяется по формуле

Адиабатная работа расширения в сопловой решетке зависит от степени реактивности ступени ρ
Состояние газа при входе в рабочую решетку определяется точкой A1. Адиабатная работа расширения газа в рабочей решетке составит

Из уравнения энергии в относительном движении газа через рабочую решетку осевой турбины, для случая энергоизолированного от внешней среды течения без потерь

Рис. 2.2. Процесс расширения газа в реактивной ступени в диаграмме — si
Выражая состояние газа перед рабочей решеткой в параметрах торможения, найдем на диаграмме -si точку 



Для активного процесса в решетке L02 = 0 и w 2t = w l. Действительная скорость w 2 выхода газа из рабочей решетки меньше w 2t вследствие потерь. Как и для сопловой решетки w 2 можно определить через коэффициент скорости рабочих лопаток φ.

По аналогии с формулой (5.3)

Потери энергии на рабочих лопатках

Для активного процесса в решетке

Состояние газа за решеткой рабочих лопаток можно определить по диаграмме -si или определить аналитически, подобно тому, как это делалось для сопел. Температура газа

Плотность и удельный объем можно определить по формулам


Если ступень активная и расширение газа на рабочих лопатках не происходит, тоР2 = P1.
Как и в сопловой решетке, процесс истечения газа в решетке рабочих лопаток можно рассчитать по законам политропного расширения.
Аналогично формулам (5.9) и (5.10) для этого случая можно найти показатель условной политропы


В общем случае величина теплового перепада в сопловых и рабочих решетках переменна по их высоте. Поэтому приведенные выше соотношения надо рассматривать как средние по высоте лопаток или относить их к определенному сечению по высоте лопатки.
Анализ уравнения сохранения энергии.
Рис.2.3. Параметры газа в контрольных сечениях струйки.
Рассмотрим объем газа между сечениями 0-0 и 1-1 в момент времени τ=0(рис.2.3). Условимся записывать работу и теплоту со знаком плюс в случае их подвода к газу и со знаком минус в случае отвода. Теплота трения всегда подводится к газу. По истечении бесконечно малого отрезка времени газ займет новое положение 
По закону сохранения энергии сумма изменений внутренней и внешней энергий газа за время dτ должна быть равна сумме подведенного иди отведенного количества теплоты и совершенной работы:
(dU + dE) d τ = dQ d τ + dL d τ , (2.9)
или для 1 кг рабочего тела:
(du + de) d τ = dq d τ + dl d τ . (2.10)
Общие количество теплоты, входящее в эти уравнения складывается из внешнего тепла q внеш, которое может быть со знаком плюс или минус, и внутреннего, эквивалентного работе сил трения

Работа внешних и внутренних сил состоит из внешней работы отданной рабочим телом или подведенной к рабочему телу, работы сил трения и работы гидродинамических сил в сечениях 0-0 и 1-1 (работы перемещения)
Следовательно, сумма работ всех сил составит


Подставив (2.11) в (2.10) и предполагая, что процесс течения идет без трения 


Выражение (2.12) получено для турбины, когда работа отводится от газа и 

Учитывая, что du + d(p v ) = di и проинтегрировав в пределах от сечения 0-0 до сечения 1-1, получим

Уравнение (2.12) и (2.13) можно применять для любого неподвижного канала (сопла, диффузора), для вращающейся решетки или колеса, для ступени турбомашин и для турбомашины в целом. При этом, параметры состояния и скорости газа во входном и выходном сечениях решетки, ступени или машины должны быть постоянными, или надлежащим образом осреднены.
В большинстве случаев процессы в турбомашинзх можно рассматривать как протекающие без теплообмена с окружающей средой, то есть адиабатные; при этом d q внеш =0
Для неподвижного канала (dl внеш = 0, ибо нет перемещения стенок канала. Тогда для изоэнтропийного (без трения) и адиабатного (с трением) процессов течения в неподвижных каналах из уравнения (2.13) получим, соответственно:

Каждое из двух этих уравнений описывает три принципиально отличных процесса течения рабочего тела в неподвижном канале:
1. Процесс идет с ускорением (разгоном) потока С1t> Со, i1t Со, i1 i0 (в действительном процессе C1 io). Потенциальная энергия газа растет за счет его кинетической энергии, которая соответственно уменьшается. Такой процесс осуществляется в диффузоре.
3. Процесс дросселированияi1t = io. При этом имеет место потеря работоспособности рабочего тела.
Располагаемая работа расширения
hc – располагаемая работа расширения в СА.Показатель адиабаты k = 1,4 – для воздухаk = 1,26 – 1,33 – для пара, или степенипонижения давления в СА
Рис. 2.4. располагаемая работа сжатия
Определение параметров течения в изоэнтропийном и реальном процессах расширения.
Широкое распространение при расчетах получили также различные диаграммы водяного пара, в особенности h,s-диаграмма. Вместе с тем следует помнить, что точность расчетов с помощью h,s -диаграммы зависит от масштаба, в котором она построена, и от пределов изменения состояния(рис 2.5).
В настоящее время взаимозависимости термодинамических свойств водяного пара представлены формулами, обеспечивающими точность согласно таблицам водяного пара или аппроксимирующие зависимости, которые обычно запрограммированы в виде различных приложений
Если предположить, что расширение пара происходит без потерь и без теплообмена с внешней средой, то этот процесс называется изоэнтропийным и изменение состояния пара подчиняется уравнению изоэнтропы
Рис. 2.5. Процесс расширения пара в канале, изображенный в h ,s -диаграмме
Истечение газа при изоэнтропийном процессе его расширения подробно рассматривается в курсе термодинамики, поэтому здесь приведены лишь основные выводы.
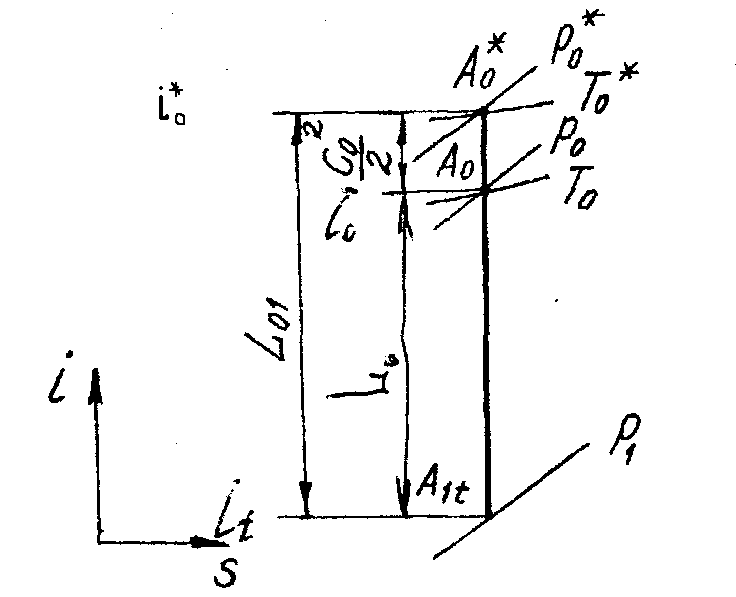
Из уравнения энергии применительно к энергоизолированномурасширению в турбинной решетке от давления Ро* до Р1 без потерь

где индекс t — указывает на то, что соответствующе параметры являются теоретическими, относящимися к расширению газа без потерь;
Lo1 — работа адиабатного расширения газа в решетке;
iо* — энтальпия, определенная по параметрам торможения ( 
Параметры адиабатно заторможенного потока связаны со статическими параметрами известными формулами


Учитывая выражение (2.34) и (2.37) получим


где 

Рис. 2.6. Изоэнтропийный процесс расширения газа в соплах.
Вследствие наличия вязкости действительный процесс истечения газа через сопло сопровождается трением частиц друг о друга, о стенки канала и вихреобразованием, что снижает скорость газа и уменьшает его кинетическую энергию. Вместе с тем, в энергоизолированном процессе по закону сохранения энергии потерянная кинетическая энергия превращается в тепло, вследствие чего температура и энтальпия протекающего газа повышаются.
Действительный процесс расширения газа в сопле происходит по некоторой условной политропеAо*A1 (рис. 2.7), причем в конечной точке процесса i1> i1t. Действительная скорость на выходе из сопла С1, очевидно, станет меньше теоретической С1t. В действительном процессе скорость истечения определяется по выражению

Потеря кинетической энергии в сопле составит


Рис. 2.7. Процесс расширения газа в сопловом аппарате
Следует заметить, что потеря кинетической энергии 
Коэффициенты потерь, скорости, расхода.
При расчете реального процесса в отличие от изоэнтропийного требует учета сил сопротивления, или коэффициентов трения, или коэффициентов потерь. Расчет каналов и характеристик потока без учета потерь может привести к результатам, существенно отличающимся от действительных. Это в свою очередь снизит эффективность турбины.
При обтекании паром стенки канала, и в частности при обтекании турбинной лопатки, влияние вязкости и вызванных ею сил трения обычно ограничивается небольшой зоной непосредственно около стенки. Скорость потока в этой зоне должна меняться от на стенке, где поток как бы «прилипает» к стенке и полностью заторможен, до скорости в так называемом ядре потока, где влияние сил трения практически уже не сказывается.
Узкая, прилегающая к стенке часть потока, где в данном сечении скорость течения возрастает от нуля до своего полного значения во внешнем потоке, называется пограничным слоем.
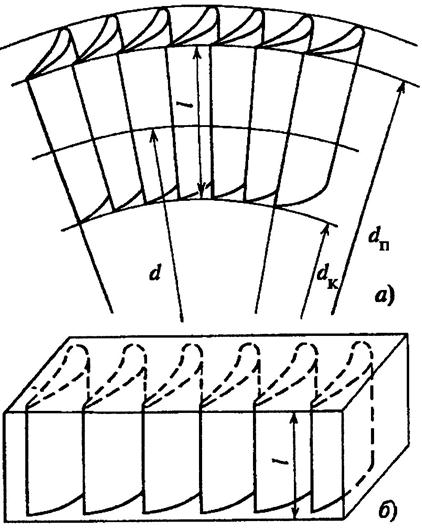
В связи с плавным характером перехода пограничного слоя в ядро потока приня-то условно считать, что пограничный слой заканчивается при толщине δ, где скорость отличается от скорости внешнего потока на 1% (рис. 2.8).
Рис. 2.8. Схема пограничного слоя при обтекании плоской стенки :
I — ламинарный режим; II — переходная зона; III — турбулентный режим; IV- ламинарный подслой; 1 — эпюра скоростей идеального потока; 2 — то же в ламинарном слое; 3 — то же в турбулентном слое; 4 — обтекаемая стенка
К.п.д. сопловой решетки
Шаг профилей в решетке оказывает существенное влияние на ее характеристики. С уменьшением шага возрастают профильные потери в связи с увеличением поверхности трения, омываемой единицей количества газа.
С увеличением шага давление на вогнутой поверхности профиля возрастает, на спинке – падает. Это, с одной стороны вызывает увеличение концевых потерь, а с другой — способствует отрыву потока на спинке, где разность давления на выходе из решетки и минимального давления возрастает. Кроме того, снижение давления на спинке при увеличении шага может вызвать появление волновых потерь.
Очевидно, для каждого типа решетки должен существовать оптимальный шаг, при котором КПД решетки достигает максимума. Оптимальные значения шага лопаток должны определяться опытным путем для конкретных решеток и условий их обтекания. Для общей ориентировки можно принять: у реактивных решеток 
Поворот потока в решетке оказывает влияние на ее КПД. Поворот увеличивается с уменьшением суммы углов β1+β2 для рабочей решетки и суммы углов α0+α1 для сопловой решетки. При этом возрастает протяженность диффузорного участка на спинке и повышается опасность отрыва потока, также повышаются концевые потери вследствие интенсификации вторичных течений. С увеличением угла поворота потока коэффициенты скорости 

Снижение относительной высоты лопаток 




Уменьшение ширины лопатки В при заданной высоте является целесообразным, так как при этом увеличивается относительная высота лопатки 


При выборе ширины рабочих лопаток необходимо помнить о том, что уменьшение ширины повлечет за собой увеличение числа лопаток и может вызвать трудность в размещении их на диске. Кроме того, в узких лопатках по прочностным и технологическим соображениям не всегда удается выдержать оптимальные толщины входной и выходной кромок. Лопатки газовых турбин чаще всего выполняются с шириной В=(0,25+0,4) 
Однако, кроме указанных факторов, надо учитывать еще утечку или подсос газа через осевой зазор, которые вызывают дополнительные искривления линий тока в периферийных областях. На основании проведенных экспериментов рекомендуется принимать величину осевого зазора в пределах 
Анализ требуемой формы соплового канала при дозвуковых и сверхзвуковых течениях.
На рис. 2.9 построены кривые, показывающие характер изменения расхода G1t, скорости истечения C1t и удельного объема V 1t в выходном сечении сопла в зависимости от отношения давлений 
Рис.2.9. Зависимость расхода через сопло, площади выходногосечения сопла, скорости и удельного объема е выходном сечении ототношения давлений
Из рисунка видно, что в области дозвукового истечения 


Опыты подтверждают увеличение расхода через сопло при уменьшении β1 в дозвуковой области истечения, но не подтверждают снижение расхода в области сверхзвукового истечения. В действительности, достигнув наибольшего значения при критическом отношений давлений, расход через сопло в дальнейшем при всех значениях 
Из рисунка 2.9 следует, что форма сопла при дозвуковом и звуковом истечении (М 1.0)сходяще-расходящейся. В сходящейся части сходяще-расходящегося сопла поток расширяется от начального давления до критического, а в расходящейся — от критического до заданного давления P1 а1, В судовыхтурбинах расширительная способность не используется.
В до звуковой области удельный объём растёт медленнее, чем скорость потока, поэтому канал должен быть сходящимся, чтобы поток разгонялся. В сверхзвуковой области удельный объём растёт быстрее, чем скорость, поэтому площадь канала должна увеличиваться (рис. 2.10).

Рис.2.10. График дозвуковых и сверхзвуковых скоростей в сопле Лаваля
В области дозвуковых течений при увеличении теплоперепада скорость растёт быстрее, чем удельный объем. В области дозвуковых течений площадь канала должна увеличиваться. При увеличении теплоперепада расход в дозвуковой области будет расти, а в сверхзвуковой будет постоянен, так как скорость достигла скорости звука.


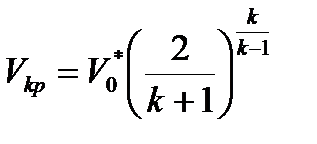

Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Преобразование энергии в турбинной ступени
Преобразование энергии в турбинной ступени, а также энергетические характеристики других элементов проточной части турбины описываются в общем случае на основе законов течения сжимаемой жидкости, которые изучаются в курсе гидрогазодинамики. В основном используются законы одномерного движения, под которым понимают такое движение жидкости, когда во всех точках поперечного сечения канала параметры жидкости (скорость, давление, удельный объем и др.) можно считать постоянным, а изменение параметров происходит вдоль канала. В реальных потоках рабочего тела в паровых турбинах параметры в поперечном сечении канала не сохраняются постоянными. Например, скорость потока вблизи стенок вследствие трения всегда ниже, чем в ядре потока.
Вторым существенным допущением при расчете потоков в проточной части турбины является предположение о неизменности параметров потока во времени, т.е. поток рассматривается установившимся.
Кроме этого делаются и другие допущения – например, об отсутствии теплообмена между потоком и стенками каналов и др.
Основными уравнениями одномерного движения сжимаемой жидкости являются:
1) уравнение состояния: 
2) уравнение неразрывности, расхода, сплошности: 
где F – площадь поперечного сечения; c – скорость; v – удельный объем.
3) уравнение количества движения: 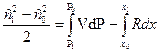
4) уравнение сохранения энергии: 
Одномерные течения в каналах разделяются на конфузорные и диффузорные.
Конфузорными называются такие течения в каналах, когда скорость рабочего тела на выходе становится больше, чем скорость на входе.
Диффузорными называются течения, в которых скорость рабочего тела уменьшается в направлении потока.
Основные уравнения одномерных потоков позволяют рассчитывать течения в каналах турбомашин. Из уравнения сохранения энергии следует, что при конфузорном течении, например, в соплах турбины, вдоль потока вместе с увеличением скорости рабочего тела уменьшается его энтальпия; в диффузорных потоках, наоборот, энтальпия растет, т.к. скорость падает.
Для расчетов одномерных потоков в каналах вводят параметры полного торможения потока в данном его сечении. Под ними в каком либо сечении понимают фиктивные параметры, которые достигаются при полном изоэнтропном торможении потока от состояния в этом сечении до нулевой скорости.
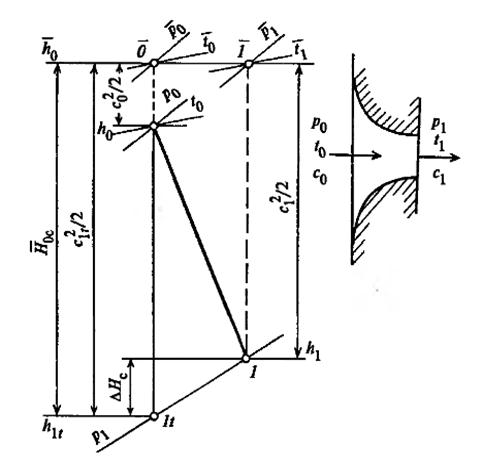
Параметры полного торможения могут быть подсчитаны с помощью h,s-диаграммы. Изобразим процесс течения рабочего тела в сопловом канале в h,s-диаграмме (рис.21).
Параметры во входном сечении сопла обозначены с индексом О, а в сечении на выходе из сопла с индексом 1, если течение реальное с потерями энергии, и с индексом 1t, если течение предполагается изоэнтропным (без потерь энергии).
Для определения скорости на выходе из соплового канала при изоэнтропном течении используем уравнение энергии, записанное для входного и выходного сечений сопла: 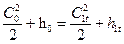
откуда теоретическая скорость на выходе из сопла 
где 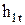

Рисунок 21 – Процесс изменения состояния в h,s–диаграмме при
истечении пара или газа через сопло
Действительная скорость потока (с потерями энергии) на выходе из сопла определяется по аналогичной формуле, полученной из уравнения энергии, записанного для входного и выходного сечений сопла по действительным параметрам потока за соплом 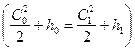

Разность энтальпий 
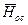
Для определения параметров полного торможения во входном сечении сопла следует на h,s-диаграмме от точки О вверх по изоэнтропе отложить отрезок 
Через точку 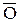

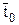

Аналогично для определения параметров полного торможения в выходном сечении сопла следует отложить в h,s-диаграмме от точки 1 вверх по изоэнтропе отрезок 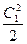
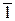


Таким образом, в потоках с потерями кинетической энергии давление полного торможения уменьшается вдоль потока.
В отличие от параметров полного торможения 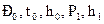
Разность энтальпий 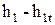



Каналы, в которых происходит плавное преобразование энтальпии в кинетическую энергию, т.е. в которых происходит ускорение потока, называется сопловыми или просто соплами.
Для характеристики потоков важными являются понятия скорости звука и критической скорости потока: 
Критической скоростью потока 
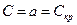
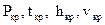
Как следует из 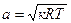
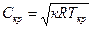
Для расчетов потока важными являются безразмерные параметры потока. К ним относятся: относительное давление 
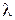
М=С/а — отношение скорости потока к скорости звука в данном сечении называется числом Маха.

Между любыми двумя безмерными параметрами легко устанавливаются функциональные зависимости, которые носят название газодинамических функций, приведенных в справочной литературе и известных из курса гидрогазодинамики.
Поскольку в состав турбинной ступени входят турбинная решетка, то вкратце остановимся на ее рассмотрении.
В паровых турбинах широко используется кольцевые турбинные решетки (рис.22), представляющие собой систему каналов, образованную установленными по кольцу одинаковыми профилями специальной формы. Все профили в решетке одинаковы, их устанавливают на равном расстоянии друг от друга и одинаковым образом. В результате между профилями образуются каналы, через которые вытекает пар.
Рисунок 22 — Модели турбинных решеток: а – кольцевой; б – прямой (плоской)
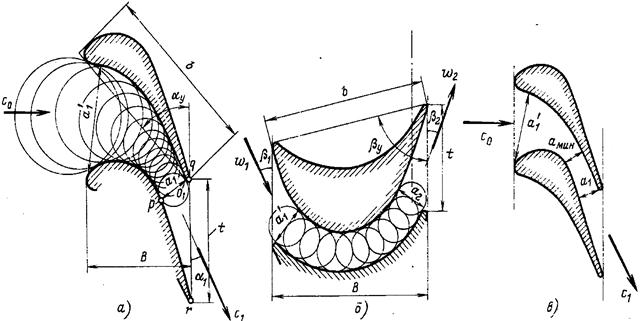
Путем изменения формы профилей и расположения их в решетке можно получать необходимую форму каналов (рис.23).
Рисунок 23 — Развертки профилей турбинных решеток: а, б — с каналами сильно и слабо уменьшающегося сечения; в — с каналами типа сопла Лаваля
Входная часть профиля называется входной кромкой, выходная – выходной кромкой, выпуклая часть – спинкой или стороной разрежения, вогнутая — стороной давления. Выходная часть канала называется косым срезом.
Течение пара в турбинных решетках подчиняется общим закономерностям, рассмотренным ранее.
Потери энергии, возникающие при течении пара через турбинную решетку, условно можно разделить на несколько составляющих. Значительную долю потерь составляют профильные, которые возникают при обтекании потоком профилей за счет появления сил трения. Имеют место также концевые потери, возникающие в концевых областях лопаток и вызывающие появление вихрей. За счет улучшения профиля лопаток, их лучшего обтекания потоком, понижаются потери.
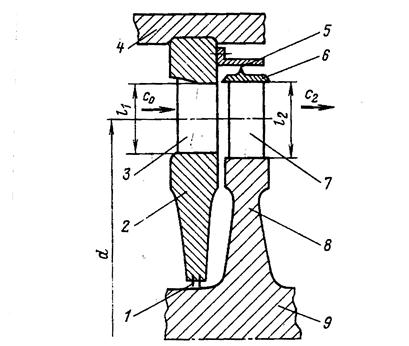
Под турбинной ступенью, как отмечалось ранее, понимается совокупность неподвижного ряда сопловых лопаток, в каналах которых ускоряется поток пара или газа, и подвижного ряда рабочих лопаток, в которых энергия движущегося пара или газа преобразуется в механическую работу на вращающемся роторе по преодолению сил сопротивления приводимой машины. На рис.24 приведено схематическое изображение турбинной ступени.
Турбинная ступень характеризуется средним диаметром ступени d и высотами сопловых l1 и рабочих l2 лопаток.
Сопловые лопатки со строго одинаковым шагом установлены в диафрагме, представляющей собой плоское, разрезанное по горизонтальному диаметру, кольцо. Сопловые лопатки образуют кольцевую решетку.
Рабочие лопатки с помощью хвостовиков набираются на диске, откованном заодно с валом или посаженном на него с натягом. Подобно сопловым лопаткам, рабочие лопатки образуют кольцевую решетку. Соседние лопатки решетки образуют рабочие каналы, через которые проходят струи пара, выходящие из сопловой решетки.
Рисунок 24 — Схематическое изображение турбинной ступени:
1 – диафрагменное уплотнение; 2 – диафрагма; 3 – сопловая решетка; 4 – корпус турбины; 5 – надбандажное уплотнение; 6 – ленточный бандаж; 7 – рабочая решетка; 8 – диск; 9 – вал
Рабочие лопатки, набранные на диске, обычно связаны по вершинам с помощью ленточного бандажа в пакеты по 2-14 шт. для увеличения надежности и экономичности ступени. Поверх бандажа часто устанавливают уплотнения для уменьшения утечки пара над бандажом. Аналогичное уплотнение устанавливают между диафрагмой и валом.
При истечении пара из сопла в среду с пониженным давлением его потенциальная энергия переходит в кинетическую. Именно такой процесс происходит в сопловых каналах турбинной установки. За счет понижения давления от значения 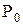

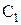
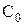
На выходе из сопловых лопаток рабочее тело (пар или газ) приобретает в процессе расширения скорость 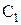
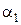
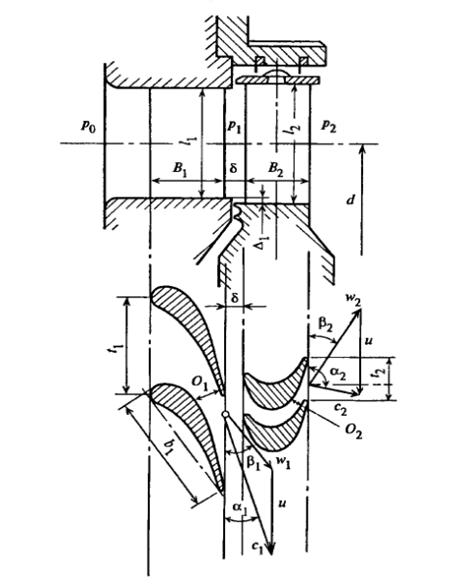
Рисунок 25 — Проточная часть осевой ступени и развертка цилиндрического сечения по среднему диаметру ступени : 
Значение этой скорости зависит от диаметра d, на котором расположены рабочие лопатки, и от частоты вращения ротора n: 
На входе в рабочие лопатки рабочее тело в относительном движении перемещается с относительной скоростью 
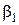
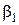


На выходе из каналов рабочих лопаток относительная скорость рабочего тела обозначается 




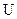





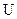

Рассмотрим процесс течения рабочего тела в турбинной ступени в h,s-диаграмме (рис.26).
Расширение рабочего тела в сопловых каналах ступени от состояния перед ступенью, определяемое точкой О, до точки 1t соответствует теоретическому (изоэнтропному) процессу течения в соплах. Реальный процесс в соплах сопровождается потерями энергии 




В соответствии с уравнением энергии теоретическая скорость потока на выходе из сопл определяется по формуле: 
Действительная скорость истечения из сопл из-за потерь энергии в соплах меньше теоретической 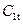

где 
Теоретический процесс расширения рабочего тела в рабочих лопатках изображается линией от точки 1 до точки 2t; разность ( 


Рисунок 26 – Процесс течения пара (газа) в турбинной ступени в h,s–диаграмме
Для потока в относительном движении в каналах рабочих лопаток уравнение сохранения энергии для сечений на входе и выходе из каналов рабочих лопаток запишется в следующем виде: 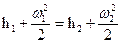
В правой части этого уравнения отсутствует член, характеризующий отводимую от рабочих лопаток к ротору турбины механическую работу, т.к. механическая работа силы взаимодействия между лопаткой и потоком в координатах движущейся лопатки равна нулю. Действительно, точка приложения этой силы не перемещается по отношению к наблюдателю, вращающемуся вместе с рабочими лопатками (условно). Перемещение точки приложения силы входит сомножителем в выражение механической работы.
По аналогии с предыдущими формулами получим выражение для определения теоретической скорости потока в относительном движении на выходе из рабочих лопаток: 
Действительная скорость на выходе из рабочих лопаток будет меньше теоретической 

где 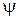
Потери энергии 

Отрезок 
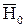

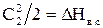

Треугольники скоростей на входе и выходе из рабочих лопаток при расчете турбинной ступени обычно совмещают вершинами в одну точку.
Для построения треугольников скоростей (рис.27) угол 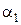


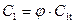
Окружную скорость по формуле:

где d – средний диаметр ротора, м;
n- частота вращения ротора, 1/с.
Рисунок 27 — Треугольники скоростей для потока пара (газа) в одновенечной турбинной ступени
Из геометрии входного треугольника скоростей определяют относительную скорость 
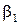






Соотношения между скоростями и углами потока в турбинной ступени в большой степени зависят от степени реактивности ступени 

Чем выше степень реактивности 
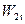

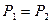



Как правило, чисто активные ступени ( 
В специальных случаях применяются ступени с отрицательной степенью реактивности. В рабочих лопатках ступени с
📺 Видео
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать

Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать

Физика - импульс и закон сохранения импульсаСкачать

Закон сохранения энергии. 9 класс. Решение задачСкачать

Урок 126. Задачи на закон сохранения энергии (ч.1)Скачать

Галилео. Эксперимент. Закон сохранения энергииСкачать

Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

Как нарушить закон сохранения энергии?Скачать

8 класс, 7 урок, Закон сохранения энергии в тепловых процессахСкачать

Применение закона сохранения и превращения механической энергии. Практическая часть. 9 класс.Скачать

Закон сохранения импульсаСкачать

Закон сохранения энергии ( шары Ньютона )Скачать

Энергия и закон сохранения энергии | Физика ЕГЭ 2023 | УмскулСкачать

Алгоритм решения задач на Закон сохранения энергииСкачать

Закон сохранения и превращения энергии. 9 класс.Скачать

Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

Урок 104. Импульс. Закон сохранения импульсаСкачать

Физика 10 класс (Урок№13 - Работа. Мощность. Энергия. Закон сохранения механической энергии.)Скачать